基于改進(jìn)粒子群算法的PID參數(shù)優(yōu)化

許森林

（200093上海市 上海理工大學(xué) 機(jī)械工程學(xué)院）

0 引言

PID控制器結(jié)構(gòu)簡(jiǎn)單、安全可靠，而且PID算法相比于其他工控算法的魯棒性好[1]，算法易于實(shí)現(xiàn)，所以在工控行業(yè)深受控制工程師的喜愛。傳統(tǒng)的PID控制相對(duì)于一些高級(jí)的控制還存在著一些不足之處，例如：精度比較差、非線性運(yùn)動(dòng)造成的誤差。PID控制的難點(diǎn)在于參數(shù)的調(diào)節(jié)，因此，我們引入智能算法來對(duì)PID參數(shù)進(jìn)行優(yōu)化。隨著科學(xué)技術(shù)的發(fā)展，大量智能群體算法應(yīng)用于工業(yè)控制領(lǐng)域。例如：基于BP神經(jīng)網(wǎng)絡(luò)和蝙蝠算法對(duì)PID參數(shù)進(jìn)行調(diào)參[2]，遺傳算法對(duì)PID控制參數(shù)整定[3]，以確保控制系統(tǒng)穩(wěn)定運(yùn)行。

Eberhart博士與Kennedy博士在1995年首次提出了模仿鳥類捕食行為的群體智能算法-粒子群算法[4]。利用群體在三維空間內(nèi)逐步尋找最優(yōu)解，對(duì)于非線性函數(shù)多值問題表現(xiàn)特別突出，PSO算法理論成熟，算法簡(jiǎn)單，全局搜索能力強(qiáng)。廖瑋霖、程杉[5]等在標(biāo)準(zhǔn)的粒子群算法的基礎(chǔ)上引入多策略融合，解決了粒子容易造成局部最優(yōu)。谷曉琳、黃明[6]等人在解決空間多維問題上，基于標(biāo)準(zhǔn)的粒子群加入慣性權(quán)重利于邏輯回歸算法動(dòng)態(tài)調(diào)節(jié)權(quán)重的值，以防粒子陷入局部最優(yōu)。本文在此基礎(chǔ)上提出了一種適合在高維復(fù)雜空間求解的新型的粒子群算法。

為了提高在高維復(fù)雜空間求解計(jì)算的效率，本文在標(biāo)準(zhǔn)的粒子群算法的基礎(chǔ)上引入小生境思想和計(jì)算機(jī)集群技術(shù)，提出了一種分布式的粒子群算法。初始化的粒子種群在不同的區(qū)間采用不同的計(jì)算機(jī)進(jìn)行計(jì)算，把各個(gè)計(jì)算機(jī)上求得的解匯總到主計(jì)算機(jī)上，從而計(jì)算出全局最優(yōu)解，加快了算法收斂速度。這種求解過程就形成了本文改進(jìn)的粒子群算法。實(shí)驗(yàn)結(jié)果表明：本文使用的算法與標(biāo)準(zhǔn)的PSO相比在求解性能和精度上表現(xiàn)更出色，在求解高維復(fù)雜空間優(yōu)化問題上有一定的參考意義。

1 數(shù)控機(jī)床伺服系統(tǒng)數(shù)學(xué)模型

數(shù)控機(jī)床各個(gè)運(yùn)動(dòng)軸構(gòu)成機(jī)床整個(gè)伺服系統(tǒng)，進(jìn)給軸的伺服系統(tǒng)能夠很清晰反應(yīng)電機(jī)受控的運(yùn)動(dòng)指令和進(jìn)給軸的實(shí)際位置變化，提高電機(jī)的運(yùn)行性能以及位置的精度，實(shí)際上也是提高了數(shù)控機(jī)床的精度，對(duì)于工業(yè)的發(fā)展具有重要意義。

被控對(duì)象是永磁旋轉(zhuǎn)伺服電機(jī)、慣性負(fù)載、滾珠絲杠為傳遞軸構(gòu)成一個(gè)被控系統(tǒng)。試驗(yàn)臺(tái)需要滿足不同要求的直線運(yùn)動(dòng)，例如：勻速直線運(yùn)動(dòng)，勻加速直線運(yùn)動(dòng)，變速運(yùn)動(dòng)，正弦函數(shù)指令運(yùn)動(dòng)。可以將這個(gè)系統(tǒng)簡(jiǎn)化為二質(zhì)量系統(tǒng)[7]。

動(dòng)力學(xué)和電學(xué)方程

根據(jù)矢量變換原理和和磁場(chǎng)定向規(guī)則，三相交流電在電機(jī)旋轉(zhuǎn)運(yùn)動(dòng)的過程中產(chǎn)生了一個(gè)旋轉(zhuǎn)磁場(chǎng)，兩項(xiàng)交流電在正交繞組時(shí)，也會(huì)產(chǎn)生磁場(chǎng)，依據(jù)矢量變換原理，上面的狀態(tài)可以得出數(shù)控伺服系統(tǒng)的框圖，見圖1。

圖1 數(shù)控伺服系統(tǒng)的框圖Fig.1 Block diagram of CNC servo system

2 PID控制器原理

PID控制是一種基于反饋控制的控制方法。這種控制方法是不斷將反饋的輸出信號(hào)與實(shí)際的命令信息進(jìn)行對(duì)比，如果出現(xiàn)了誤差e(s)，此時(shí)，PID控制系統(tǒng)就會(huì)產(chǎn)生反饋信號(hào)，發(fā)送一個(gè)控制信號(hào)，使得偏差不斷減小，持續(xù)發(fā)送指令信號(hào)給被控設(shè)備，使其偏差減小，達(dá)到輸出量與輸入指令一致。

在PID控制系統(tǒng)中，控制器的設(shè)計(jì)對(duì)系統(tǒng)的各種伺服狀態(tài)起到了決定性作用，影響被控設(shè)備工作的整體性能。為了被控設(shè)備及控制系統(tǒng)的穩(wěn)定性，實(shí)現(xiàn)對(duì)運(yùn)動(dòng)軌跡規(guī)劃的精準(zhǔn)執(zhí)行，必須對(duì)控制系統(tǒng)進(jìn)行研究。

目前常用的PID算法是一種易于實(shí)現(xiàn)、穩(wěn)定性高的控制方式。其典型的組成環(huán)節(jié)如下：

（1）比例控制

比例控制對(duì)系統(tǒng)的影響會(huì)改變信號(hào)輸出的增益，對(duì)信號(hào)的相位不會(huì)造成延遲等影響。如圖2所示為比例控制的結(jié)構(gòu)示意圖。

圖2 比例控制Fig.2 Proportional control

當(dāng)系統(tǒng)產(chǎn)生偏差之后，比例環(huán)節(jié)就會(huì)對(duì)系統(tǒng)產(chǎn)生控制作用，偏差越大，比例環(huán)節(jié)的作用能力就越強(qiáng)，從而減小系統(tǒng)的偏差，達(dá)到理想的輸入。比例環(huán)節(jié)的KP過小則很難起到作用；但過大的KP會(huì)超出系統(tǒng)的穩(wěn)定性裕度，使得系統(tǒng)不穩(wěn)定。因此，為了使系統(tǒng)保持穩(wěn)定，需要考慮系統(tǒng)超調(diào)量來約束比例增益KP的取值。同時(shí)，當(dāng)系統(tǒng)僅在比例控制下時(shí)會(huì)產(chǎn)生穩(wěn)態(tài)誤差，這就需要引入其他環(huán)節(jié)與比例環(huán)節(jié)配合進(jìn)行系統(tǒng)的控制。

式中：u(t)——控制信號(hào)；KP——比例增益；e(t)——誤差信號(hào)；r(t)——參考信號(hào)；y(t)——反饋信號(hào)。

（2）積分控制

偏差信號(hào)的積分與積分控制的作用力與成正比，通過引入積分項(xiàng)能消除被控設(shè)備與指令的誤差，如圖3所示。

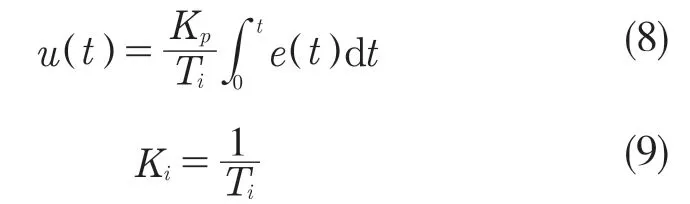
式中：Ti——積分時(shí)間常數(shù)；Ki——積分增益。

圖3 積分控制Fig.3 Integral control

理想情況下，當(dāng)系統(tǒng)產(chǎn)生偏差時(shí)，即使誤差在偏小的情況下，積分項(xiàng)也可以隨著時(shí)間而增長，因此，積分項(xiàng)就可以調(diào)整控制器，直到穩(wěn)態(tài)誤差的減小為0。積分環(huán)節(jié)能夠有效地消除外力和比例控制帶來的余差、超調(diào)和振蕩等穩(wěn)態(tài)誤差，但同時(shí)也會(huì)產(chǎn)生使系統(tǒng)的動(dòng)態(tài)響應(yīng)變慢等缺點(diǎn)。

（3）微分控制

微分控制如圖4所示。其對(duì)于系統(tǒng)的穩(wěn)態(tài)不起作用，只影響系統(tǒng)的動(dòng)態(tài)調(diào)節(jié)過程，在系統(tǒng)中引入微分控制可以顯著提高控制系統(tǒng)的穩(wěn)定性與快速響應(yīng)能力。

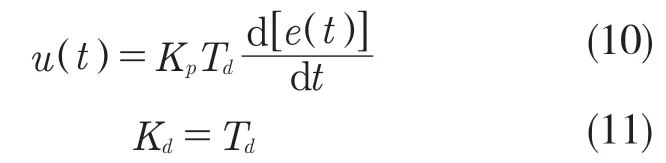
式中:Td——微分時(shí)間常數(shù)；Kd——微分增益。

圖4 微分控制Fig.4 Differential control

對(duì)于微分控制，在輸入量信號(hào)與輸出量信號(hào)的偏差為0時(shí)也可以起到作用，因?yàn)槲⒎挚刂颇軌蝾A(yù)測(cè)偏差的變化，具有超前控制的能力。微分環(huán)節(jié)的超前反應(yīng)可以對(duì)未來的輸入與輸出的偏差進(jìn)行估計(jì)，從而提高系統(tǒng)的動(dòng)態(tài)表現(xiàn)。

PID對(duì)偏差e(t)進(jìn)行比例、微分控制和積分控制，然后對(duì)其組合形成每個(gè)伺服周期的控制量u(t)，從而使輸出達(dá)到理想的響應(yīng)[8]。PID控制的時(shí)域微分方程為

為了實(shí)際中對(duì)PID算法的一般需要，對(duì)PID算法進(jìn)行離散化，離散化后的PID算法公式為

式中:T——采樣時(shí)間間隔；e(x)——X時(shí)刻的系統(tǒng)偏差量。

3 標(biāo)準(zhǔn)PSO算法原理

粒子群算法的搜索過程和鳥類的捕食行為類似，粒子代表著鳥類，搜索范圍就是鳥類搜尋食物的區(qū)域，在這個(gè)區(qū)域內(nèi)有一塊食物，即是全局最優(yōu)解。一開始鳥群中的鳥作為單獨(dú)的個(gè)體分散在這一區(qū)域中，有的鳥距離食物較近就會(huì)朝著食物飛去，由于鳥群的集體行為，其他鳥群也會(huì)跟著這個(gè)鳥的方向飛，搜尋這個(gè)鳥的附近區(qū)域，直到找到這塊食物。

粒子群算法（PSO）是通過粒子的不同位置分布與迭代對(duì)目標(biāo)進(jìn)行優(yōu)化的智能算法。設(shè)解空間為S維的搜索空間，每個(gè)粒子可看作一個(gè)向量，第i個(gè)粒子的位置可表達(dá)為，在解空間的飛行速度可以表達(dá)為，其中，m為粒子種群個(gè)數(shù)。粒子每次迭代會(huì)根據(jù)其當(dāng)前的適應(yīng)度產(chǎn)生局部極值和全體極值，然后粒子會(huì)依賴當(dāng)前自身與種群的歷史最優(yōu)解去更新粒子新的速度與位置。設(shè)在S維的搜索空間，第i個(gè)粒子搜索過程中的最佳位置為種群的最佳位置為則粒子的更新公式如下：

式中：i∈[1，m]；s ∈[1，S]；c1，c2——非負(fù)的更新系數(shù)；r1，r2——沒有依賴關(guān)系的獨(dú)立偽隨機(jī)數(shù)。

種群中的粒子在解空間中任何一個(gè)所處的位置均可以看成當(dāng)前所求優(yōu)化問題的潛在解。而粒子極值的求解通過適應(yīng)度函數(shù)來確定，一般設(shè)適應(yīng)度函數(shù)為優(yōu)化目標(biāo)函數(shù)。設(shè)f(x)為適應(yīng)度函數(shù)，判斷當(dāng)前的粒子i是不是為解空間中的最佳位置可表達(dá)為

PSO算法的流程如圖5所示，具體步驟如下：

圖5 PSO算法流程圖Fig.5 PSO algorithm flowchart

（1）根據(jù)實(shí)際問題的搜索范圍和參數(shù)個(gè)數(shù)確定粒子的維度和個(gè)數(shù)，在搜索范圍內(nèi)隨機(jī)初始化粒子群的位置和速度，并設(shè)定種群的初始局部最優(yōu)值和全局最優(yōu)值。

（2）適應(yīng)度函數(shù)是用來確定每個(gè)粒子的個(gè)體適應(yīng)度值。將每個(gè)粒子的歷史記錄中最優(yōu)的值作為粒子當(dāng)前的個(gè)體極值；將所有粒子的歷史最優(yōu)適應(yīng)度值作為種群的群體極值，并記錄對(duì)應(yīng)的位置信息。

（3）由式（15）、式（16）計(jì)算并更新每個(gè)粒子的位置和速度信息，并根據(jù)限制范圍保證粒子不超出搜索界限。

（4）檢驗(yàn)最優(yōu)值是否滿足結(jié)束條件或者是否等于最大進(jìn)化代數(shù)，如果等于最大迭代次數(shù)則停止迭代并輸出最終結(jié)果，否則繼續(xù)步驟（2）。

4 改進(jìn)的PSO算法

從基本的PSO算法的優(yōu)化機(jī)制分析可知，標(biāo)準(zhǔn)PSO算法的初始化種群的優(yōu)劣會(huì)直接影響算法的優(yōu)化結(jié)果。標(biāo)準(zhǔn)的PSO算法是隨機(jī)生成的初始種群，在迭代的過程中極其容易造成局部最優(yōu)值。如果標(biāo)準(zhǔn)PSO算法的初始化種群過于分散，有可能在迭代優(yōu)化的過程中造成收斂過慢、嚴(yán)重的會(huì)造成收斂消失。因此，本文引入小生境技術(shù)和分布式原理[9]，在PSO算法機(jī)制中對(duì)初始種群的各個(gè)區(qū)間段進(jìn)行分段式同時(shí)求解，分別求取不同階段上的局部最優(yōu)解，將所有的解匯聚到一起，從而找到全局最優(yōu)解。DNPSO按區(qū)間分布式求解示意圖如圖6所示。

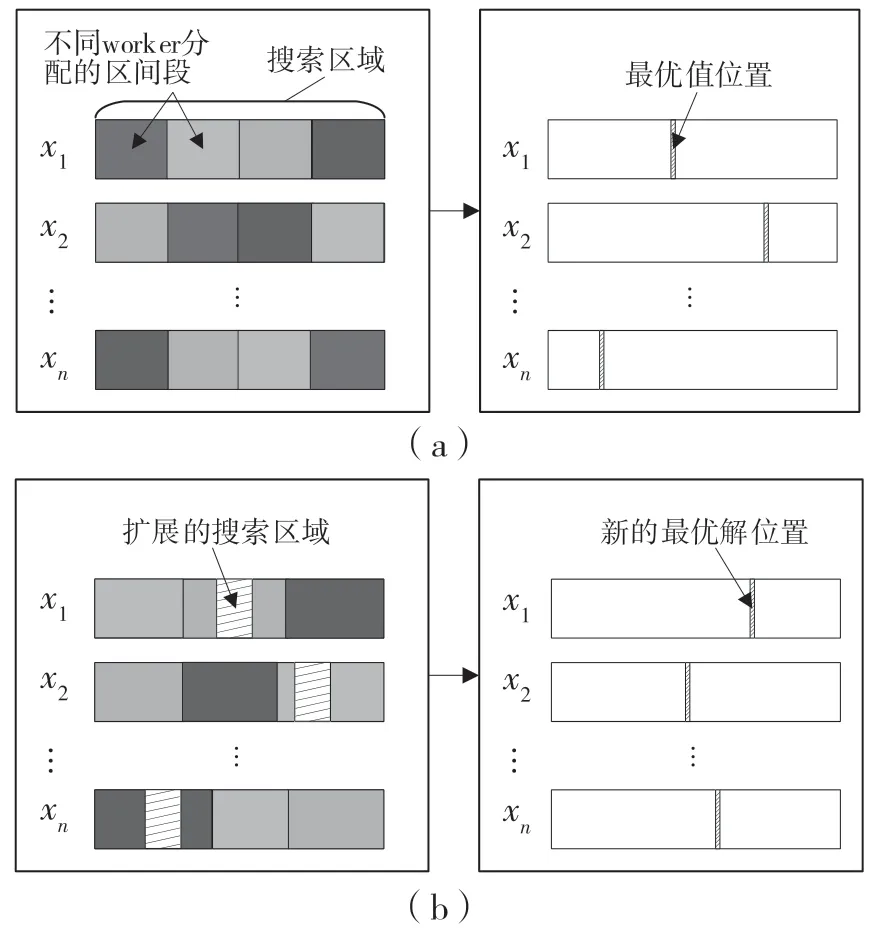
圖6 DNPSO分布式求解示意圖Fig.6 Schematic diagram of DNPSO algorithm distributed solution

PSO優(yōu)化算法缺乏速度的動(dòng)態(tài)調(diào)節(jié)，對(duì)復(fù)雜問題的搜索中很難獲得很好的效果。種群數(shù)量和初始化的隨機(jī)性分布對(duì)PSO算法的影響較大，粒子數(shù)量的增加可以提升算法搜索的準(zhǔn)確性，提升效果非常明顯，但是過多的粒子數(shù)量會(huì)引起計(jì)算機(jī)計(jì)算量的增加，使得計(jì)算時(shí)間較長；而如果粒子的數(shù)量設(shè)置得較少，雖然能減少計(jì)算的時(shí)間，但是會(huì)使得算法中粒子的多樣性大大減少，從而極有可能丟失最優(yōu)極值點(diǎn)。Shi Y和Eerhart[10]引入了慣性權(quán)重系數(shù)ω加快粒子的求解速度，因此粒子的更新公式可以表達(dá)為

式中：ω——非負(fù)的慣性權(quán)重系數(shù)，慣性權(quán)重可以調(diào)節(jié)粒子的飛行速度，從而加快算法的種群搜索能力與個(gè)體搜索能力。PSO算法在粒子迭代中，慣性權(quán)重系數(shù)可以調(diào)整當(dāng)前粒子求優(yōu)的速度與前一次搜索的關(guān)系。但是，若ω的值太小，會(huì)導(dǎo)致算法優(yōu)化能力降低，從而使粒子提前陷入局部最優(yōu)解，從而使最終的優(yōu)化結(jié)果僵化。

為了更好地求出全局最優(yōu)解，本文采用隨機(jī)的動(dòng)態(tài)權(quán)重ω的方法對(duì)粒子群算法進(jìn)行改進(jìn)[11]。ω的表達(dá)式為：

式中：N（0，1）——符合標(biāo)準(zhǔn)正態(tài)分布的隨機(jī)數(shù)；rand（0，1）——位于0到1之間的隨機(jī)數(shù)。若ω為恒定值，會(huì)導(dǎo)致粒子不收斂，但是如果將ω設(shè)置為隨機(jī)分布，那么就可以利用動(dòng)態(tài)地改變?chǔ)刂担沟蒙洗蔚乃俾蕦?duì)當(dāng)前的種群內(nèi)粒子的優(yōu)化搜尋速度形成動(dòng)態(tài)的影響，再結(jié)合小生境思想，對(duì)各個(gè)階段求得最優(yōu)解，可以有效避免陷入局部最優(yōu)解。

DNPSO的算法具體進(jìn)化步驟如下：

Step1：初始化算法的基本參數(shù)，定義集群的worker數(shù)量、各變量的搜索范圍和擴(kuò)展步長。

Step2：根據(jù)worker的數(shù)量分配粒子的個(gè)數(shù)，再將各個(gè)變量的搜索范圍分成等長的區(qū)段，每個(gè)worker在各個(gè)變量中隨機(jī)但不重復(fù)地選擇一個(gè)區(qū)段并組合，并在這些區(qū)段范圍內(nèi)初始化粒子的位置和速度。

Step3：根據(jù)式（15）和式（16）在每個(gè)worker中獨(dú)立地執(zhí)行粒子群算法，返回局部最優(yōu)位置和適應(yīng)度至client。

Step4：分別求解對(duì)應(yīng)區(qū)間段上的局部最優(yōu)解，最后把所有局部最優(yōu)解匯總到主機(jī)進(jìn)行全局最優(yōu)解的求解，并以該位置為中心減去和加上半個(gè)搜索步長，創(chuàng)建新的搜索區(qū)段加入到下一次的搜索中。

Step5：?jiǎn)为?dú)分配一個(gè)worker去搜索擴(kuò)展的區(qū)間，然后根據(jù)剩余的worker數(shù)量重新分段各個(gè)變量的搜索范圍，并初始化粒子后分配給空閑的worker。

Step6：返回至step3直到滿足算法停止條件，輸出結(jié)果。

5 改進(jìn)粒子群算法的PID參數(shù)優(yōu)化和仿真研究

先建立MATLAB仿真模型，用來驗(yàn)證基于DNPS算法PID控制器的有效性。

初始化粒子種群為30；慣性權(quán)重w=0.9,學(xué)習(xí)因子 c1，c2取2；最大迭代次數(shù)為100代。采用不同的算法分別PID控制器參數(shù)優(yōu)化以及階躍響應(yīng)。實(shí)驗(yàn)結(jié)果如圖7和圖8所示。

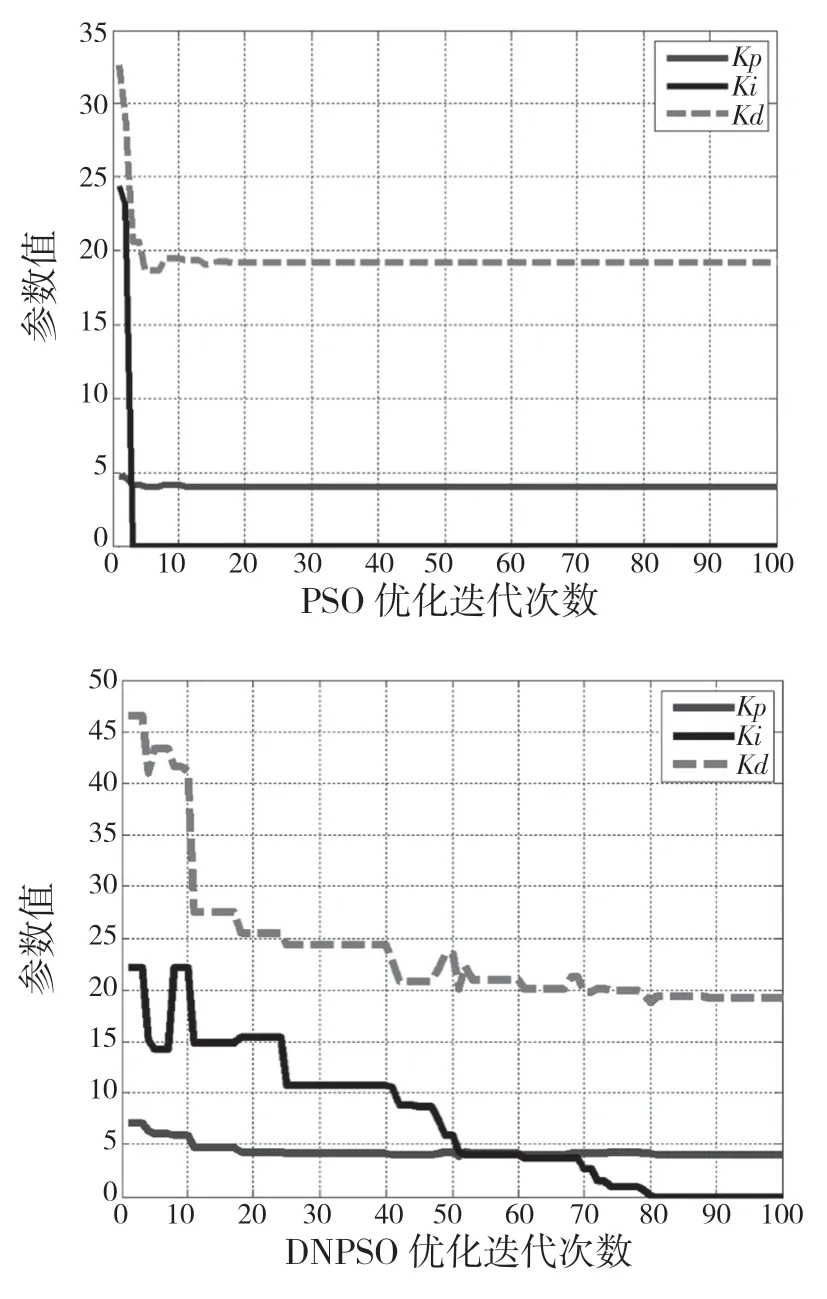
圖7 PID控制器參數(shù)優(yōu)化曲線Fig.7 PID parameter optimization curve

從圖7作圖 DNPSO優(yōu)化迭代次數(shù)圖可以看 出PID參數(shù)優(yōu)化結(jié)果 為KP=4.067；Ki=0；Kd=19.279 6。從圖8階躍響應(yīng)仿真曲線上可以看出，應(yīng)用改進(jìn)的PSO算法的控制器與傳統(tǒng)的PSO算法對(duì)比，被控對(duì)象有很明顯的減少系統(tǒng)的響應(yīng)。

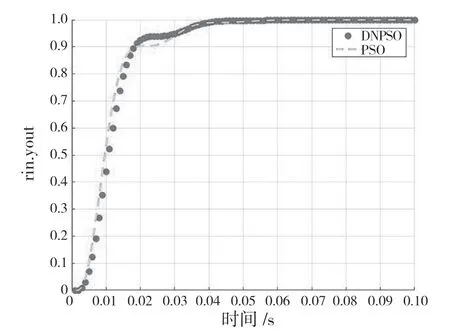
圖8 階躍響應(yīng)仿真曲線Fig.8 Step response simulation curve

結(jié)合數(shù)控伺服系統(tǒng)的數(shù)學(xué)模型進(jìn)一步研究DNPSO控制器的性能，建立二質(zhì)量伺服系統(tǒng)的仿真模型。采樣時(shí)間為0.001 s,輸入正弦信號(hào)指令，速度環(huán)中外加干擾Tf摩擦模型。利用改進(jìn)的PSO算法優(yōu)化得PID控制器對(duì)伺服控制系統(tǒng)進(jìn)行正弦信號(hào)位置跟蹤，并與傳統(tǒng)的PSO算法優(yōu)化的PID控制器進(jìn)行對(duì)比分析仿真。圖9為基于改進(jìn)PSO優(yōu)化下正弦信號(hào)位置跟蹤。圖10為基于標(biāo)準(zhǔn)PSO優(yōu)化下正弦信號(hào)位置跟蹤。

正弦信號(hào)為

Tf摩擦模型為

從圖9和圖10仿真分析結(jié)果可以明顯看出，在摩擦模型時(shí)，基于改進(jìn)的PSO算法的PID控制器在正弦信號(hào)下位移的跟蹤與理想位置偏差非常小，而由標(biāo)準(zhǔn)PSO算法優(yōu)化過后被控對(duì)象的位移跟蹤與理論狀態(tài)的位移有較大偏差。此外，在優(yōu)化時(shí)間上，本仿真采用1臺(tái)主機(jī)、4臺(tái)分機(jī)分布式對(duì)伺服系統(tǒng)PID控制器參數(shù)進(jìn)行優(yōu)化，采用改進(jìn)的粒子群算法能夠避免粒子陷入局部最優(yōu)解，從而節(jié)約大量?jī)?yōu)化時(shí)間。

圖9 基于改進(jìn)PSO優(yōu)化下正弦信號(hào)位置跟蹤Fig.9 Position tracking of sinusoidal signal based on DNPSO

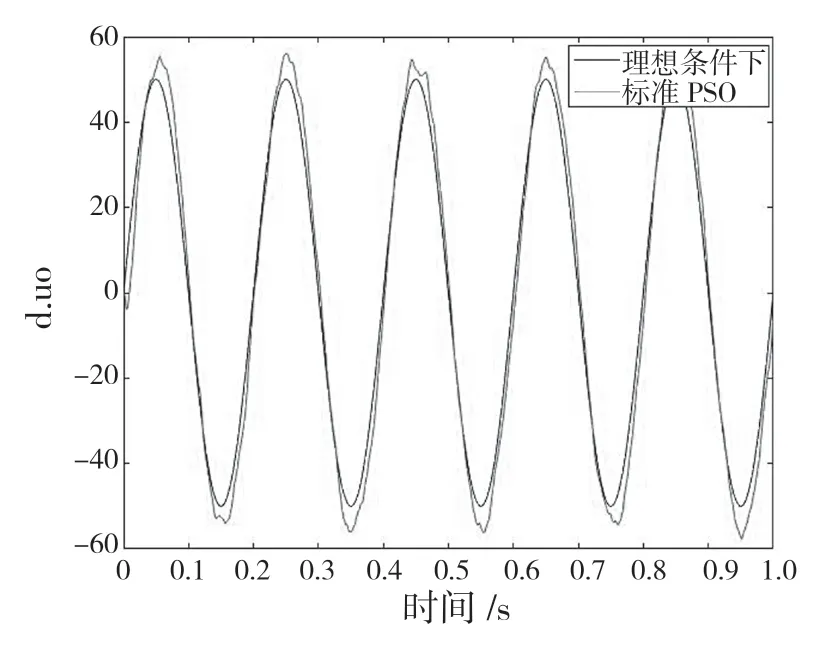
圖10 基于標(biāo)準(zhǔn)PSO優(yōu)化下正弦信號(hào)位置跟蹤Fig.10 Position tracking of sinusoidal signal based on PSO

6 結(jié)論

本文通過引入小生境思想提出了一種對(duì)初始化后的種群按照區(qū)間進(jìn)行分段的方法，同時(shí)引入了動(dòng)態(tài)加權(quán)因子來對(duì)標(biāo)準(zhǔn)POS算法進(jìn)行改進(jìn)。MATLAB仿真實(shí)驗(yàn)圖9和圖10表明，本文所提出的改進(jìn)的粒子群能夠很有效地精確獲取全局最優(yōu)值，減少了優(yōu)化迭代的時(shí)間，對(duì)整個(gè)工控行業(yè)具有重要的參考價(jià)值。