GPS高程測量數據處理分析及擬合方法研究

張建威，李 江

(1.河南能源化工集團 永煤公司車集煤礦，河南 永城 476600； 2.河南能源化工集團 永煤公司，河南 永城 476600)

20世紀70年代，美國首先建立了全球定位系統，世界各地開始對GPS定位技術開始研究，也逐漸擴展到利用GPS高程的測量中。20世紀80年代初，中國也開始對GPS技術進行研究，把GPS接收機應用于多個領域中。20世紀90年代，國內外學者對GPS高程測量數據處理分析及擬合方法進行了大量的研究。于素君[1]對石油物探GPS控制測量理論和方法進行了研究，以石油勘探中地震勘探測線的布設問題為主線，提出了一種基于穩健估計的曲面擬合法，分析了GPS數據及控制測量處理方法和符合物探施工精度要求的導線測量；劉俊領等[2]研究了GPS高程擬合方法，分析了GPS高程精度要求、擬合方法，經試驗論證，GPS高程擬合的相應數學模型對地質高程的擬合具有一定的成效；解祥成等[3]分析了GPS擬合高程代替五等水準測量精度，分析了GPS高程轉換的過程，研究了數學模型擬合法，并對某地區GPS水準高程和擬合高程的精度進行了對比分析，最后利用GPS觀測值加已知高程點擬合，對待定點高程的求解方法進行了詳細研究。

1 GPS水準測量的誤差分析

1.1 誤差源

GPS測量模式是影響GPS測量大地高精度的主要因素。為了減小誤差，利用雙頻接收機、差分技術靜態觀測進行觀測，其垂直精度和水平精度得到了明顯的提高。但是，根據具體精度要求、設計經費和外部條件，需要對GPS的觀測方法進行綜合考慮。

GPS水準測量的誤差來源主要是地面接收站、衛星信號傳播站和GPS衛星。不同等級水準測量的精度可以用每千米高差中數的全中誤差(MW)和偶然中誤差(MΔ)。不同等級水準測量精度指標[4-5]見表1。

表1 不同等級水準測量精度指標Tab.1 Different levels of leveling accuracy indicators

當完成閉合環或附合線路測量時，如構成水準網的環數>20，應計算每公里高差中數的全中誤差：

(1)

(2)

式中，N為水準環數目；F為水準環長度；W為各項改正后閉合差；R為測段長度；Δ為往返高差不符值。

1.2 提高測量精度的措施

由實踐經驗和理論分析可知，主要有以下提高測量精度的措施[6-9]。

(1)提高測定大地高的精度。①采取方法提高GPS網基線解算的坐標精度；②減弱對流層延遲誤差和多路徑誤差；③當進行觀測時，選擇最佳的衛星部分；④選擇最優的雙頻GPS接收機；⑤對GPS星歷的精度進行改善。

(2)提高聯測幾何水準的精度。①當GPS網有特殊精度要求，采用二等精密水準進行聯測；②當測量誤差占GPS水準總誤差的30%時，應采用三等幾何水準進行聯測。

(3)提高GPS水準計算精度。①采用抗差估計法，對計算數據中某點精度不高或粗差；②選擇模型時，應優選對綜合模型進行考慮；③選擇已知點時，應選擇具有代表性且均勻分布的測點。

2 模型參數的抗差估計

本文主要分析多項式擬合模型的抗差估計和模型參數的優選，先分析基于權陣迭代抗差估計的多項式模型參數的抗差估計。選擇客觀的權陣是獲取估計值的保證，權陣表達式：

(3)

當GPS所測的大地高協方差設置為∑hh，則幾何水準得到正常協方差陣為∑HH，則權陣的表達式：

P=∑-1=(∑hh+∑HH)-1

(4)

當把已知點的高程異常值ξ=h-H是高精度的，則初始權陣P，可根據已知點到待求點的已知距離來進行計算：

(5)

式中，e為一個較小的數；Di為已知點i到待求點的距離；C0為單位權值。

引入抗差估計方法的目的：避免粗差對模型參數估計產生不良影響。簡單實用的迭代公式：

(6)

式中，n是最小二乘原則下迭代得到誤差方程的次數。

測量數據處理中的權函數：

(1)丹麥法。表達式：

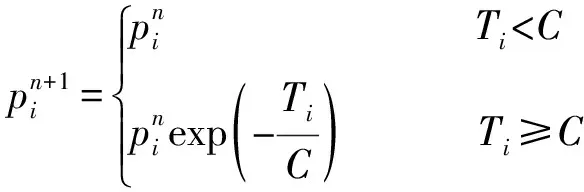
(7)

式中，C為常量，一般取值為3.0或2.5。

(2)Hubber方案。表達式：

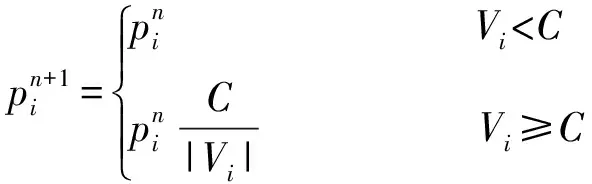
(8)

式中，C為常量，一般為2倍中誤差。

(3)IGGⅢ方案。表達式：

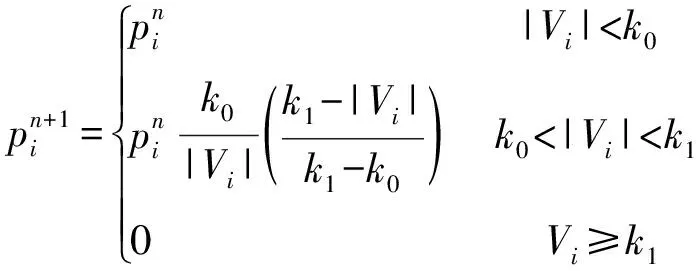
(9)

式中，k0為1.5倍的中誤差；k1為2.5倍的中誤差。

由式(7)—式(9)可知，通過不斷迭代的解算誤差方程，一般正常數據的權值比誤差較大的已知數據的權值小，從而把粗差數據從已知數據中進行剔除。

3 GPS高程擬合模型的選擇

3.1 擬合結果的精度評定

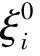
(10)

式中，n為參與計算的已知點。

(2)外符精度。GPS水準的外符精度M：

(11)

式中，n為參與檢核的點數。

GPS高程轉換模型參數優選流程如圖1所示。

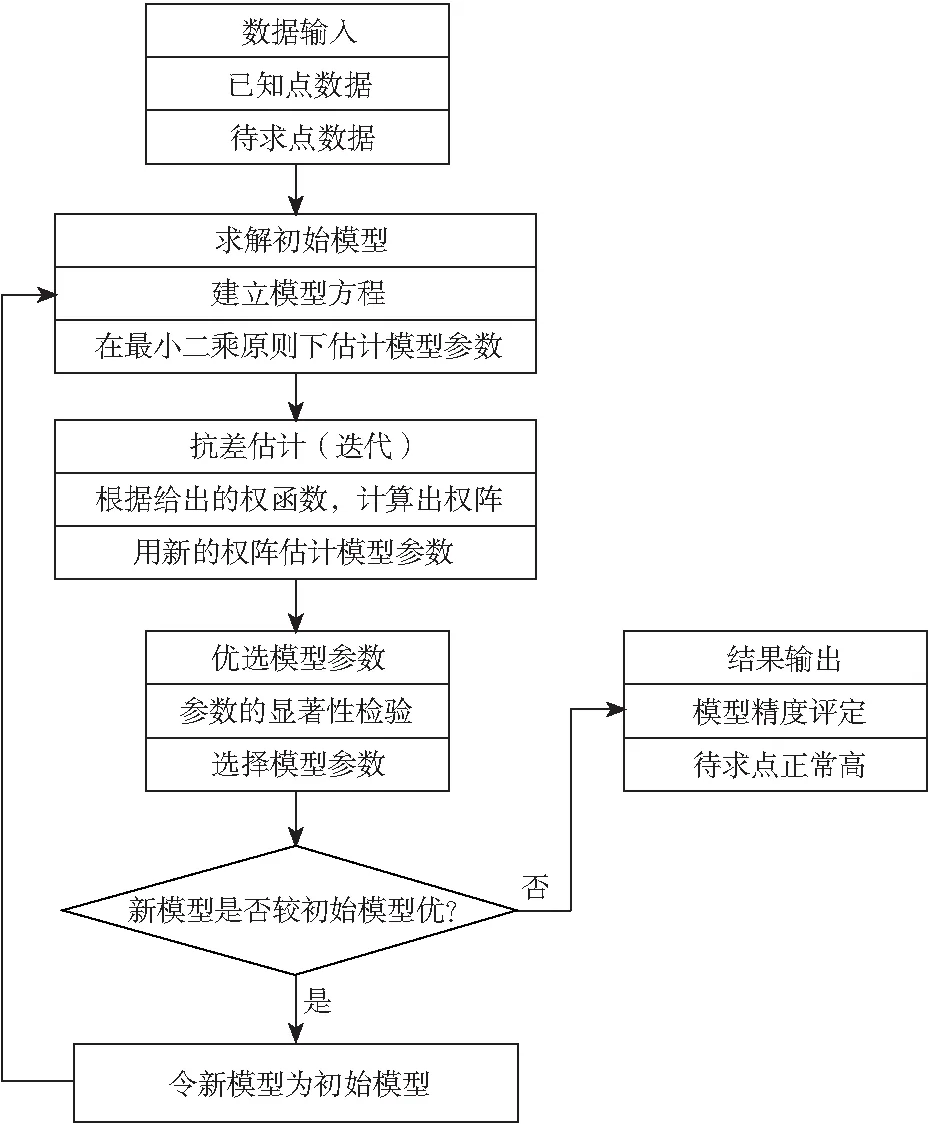
圖1 GPS高程轉換模型參數優選流程Fig.1 GPS elevation conversion model parameter optimization process

GPS水準相對精度評定方法：①閉合差檢核；②相對誤差檢核。

假設檢核點到已知點的距離為L，基于水準限差的檢核點擬合殘差的限值見表2，然后將限值和殘差作比較，做GPS高程精度評定。

表2 基于水準限差的檢核點擬合殘差的限值Tab.2 Limit of fitting residuals based on level tolerance

3.2 AIC準則

AIC準則是由Akaike基于信息論的角度提出的，該準則樹要用于模型的選擇和頂階上，從而獲得理想的結果，采用AIC準則，對模型進行分析對比，得出模型的檢核誤差和內附誤差，然后得到2個AIC值：AICc和AICi，兩者相加得到AICt。最后對兩者的信息進行比較，來確定模型的好壞。

AIC準則的表達式：

AIC=logσ2+(2m+3/n)

(12)

式中，n為代入計算值的個數；m為所選模型的參數，其中m≤n。

在GPS高程轉換過程中，二次曲面模型時，m=6；三次曲面模型時，m=10；平面模型時，m=3。

4 應用實例

某測區整體較為平坦，測區長25.0 km，寬13.0 km，總面積為325.0 m2。測區有3個200～300 m的山包，測區共有27個水準聯測點，選擇11個檢核點、16個擬合點。為了盡量減少點位之間的影響，選擇16個擬合點均分布在測區中。測區測點點位分布如圖2所示。

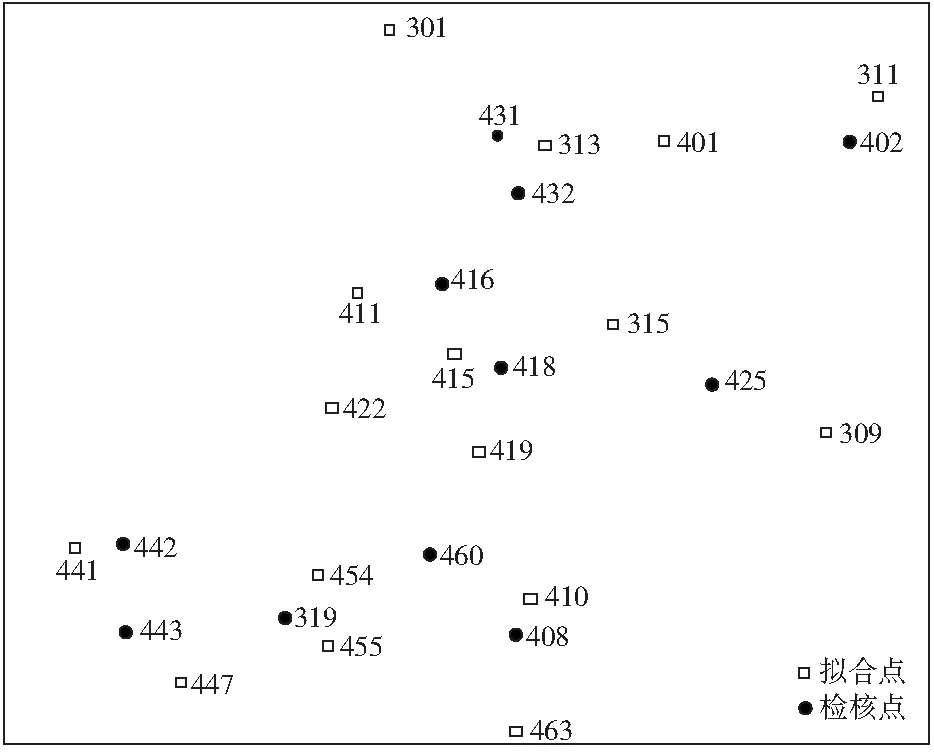
圖2 測區測點點位分布Fig.2 Point distribution of measurement points

當測量數據進行粗差剔除后，采用混合模擬模型、綜合擬合模型、多面函數擬合模型、三次曲面擬合、二次曲面擬合，對水準聯測數據進行檢驗和擬合，其檢驗和擬合的結果見表3。

表3 不同模型對水準聯測數據進行檢驗和擬合結果Tab.3 Different models test and fit joint level test data

由表3可知：

(1)檢核點的高程異常大于擬合點，說明該擬合模型是根據擬合點高程異常數據組建的。

(2)混合模型和綜合模型的擬合精度要明顯優于單一模型(多面函數、三次函數、二次函數)的擬合效果。

(3)在11個檢核點中，有2個點的擬合精度較高，分別為319檢核點、418檢核點；在17個擬合點中，有3個點的擬合精度較高，分別為313擬合點、410擬合點、415擬合點，根據這5個點的分布情況，該5個點位于水準聯測點相對密集的位置，表明增加水準聯測點，有助于提高擬合精度。

為了清晰地對各個模型的模擬結果進行比較，采用AIC準則，驗證模型的有效性，分別對5種模型擬合結果的AIC值、最小值、最大值和標準值進行計算。實例中模型的精度和AIC值見表4。

由表4可知：根據最小值、最大值、標準差分析，綜合模型和混合模型的模型精度優于單一模型，其AIC值也明顯高于單一模型，表明，采用AIC準則優于對模型的優劣進行評判。

表4 實例中模型的精度和AIC值Tab.4 Accuracy and AIC value of the model in the example

5 結論

通過GPS水準測量的誤差分析、模型參數的抗差估計、GPS高程擬合模型的選擇以及現場應用，分析了GPS高程測量數據流程，然后分別以混合模擬模型、綜合擬合模型、多面函數擬合模型、三次曲面擬合、二次曲面擬合對水準聯測數據進行檢驗和擬合，研究了各個模型的精度和AIC值，研究為不同資料、不同地形高程測量數據的擬合提供了借鑒。