EC細網格產品在復雜海島地形條件下的大風滾動訂正釋用

於敏佳，劉菡，王倩，胡瀟杰

（舟山市氣象局，浙江舟山316000）

1 引言

舟山地處中緯度地帶，是“絲綢之路經濟帶”和“21世紀海上絲綢之路”的交匯點，區位優勢明顯。習近平總書記2015年視察舟山時指出：“舟山港口優勢、區位優勢、資源優勢獨特，其開發開放不僅具有區域性的戰略意義，而且具有國家層面的戰略意義”。舟山港航經濟發展蓬勃，寧波-舟山港連續10 a貨物吞吐量全球第一，寶鋼馬跡山、岙山興中和新奧舟山LNG等港口也承接著大量的礦石中轉和油氣儲運等業務。然而，舟山災害性天氣四季頻發，年平均8級以上大風日數142.7 d，其中8～9級大風日數129.2 d，10～11級大風日數12.7 d，12級以上大風日數0.8 d[1]。同時舟山群島地形復雜，舟山沿海各海域受島嶼和山系遮蔽影響，使得各海域風力具有明顯的局地性特征[2]。針對舟山各港口風力局地性特點，業務上已開展了各港口風力專業專項預報服務。經過多年的EC數值模式預報與站點實況風力對比，已得出各港口風力預報實況偏差的定性經驗判斷，但并未獲得精確定量的訂正數值。因此，應用EC細網格數值預報產品，做好舟山各港口風力預報釋用，為舟山港航經濟發展提供氣象保障，具有十分重要的意義。

關于數值預報產品的釋用，目前我國已有較多的科技人員進行了深入研究。唐躍等[3]采用雙線性內插法和滑動平均誤差法，進行舟山港口大風的本地化釋用，并建立了各類指標和預報模型。張娟等[4]將BP（Back Propagation）人工神經網絡引入到風暴潮數值預報的解釋應用中，對風暴潮的數值預報結果進行訂正；陳德花等[5]應用BP人工神經網絡方法對MM5中尺度數值模式進行了福建沿海大風的釋用；黨英娜等[6]應用極差分析訂正的方法對T639和MM5數值模式產品進行釋用；陳豫英等[7]利用MM5模式的站點輸出產品，采用多元線性和逐步回歸的模式輸出統計方法（Model Output Statistics，MOS）進行風的精細化釋用；金龍等[8]利用模塊化模糊神經網絡方法進行數值預報產品釋用；劉鴻升等[9]設計了最大值-閥值綜合集成法，利用歐洲中期天氣預報中心（European Centre for Mediumrange Weather Forecasts，ECMWF）中期數值預報，進行了偏北大風的數值預報釋用；李江萍等[10]初步探討了統計降尺度法在數值預報產品釋用中的應用；錢燕珍等[11]將支持向量機（Support Vector Machine，SVM）回歸方法應用于近海和登陸熱帶氣旋的強度預報，對全球預報系統（Global Forecast System，GFS）數值預報產品進行了釋用。以上方法都提高了預報準確率，取得了一定的釋用效果，但對于地形的風力影響研究較少，且隨著模式預報水平的不斷改進，釋用模型也應隨之更新。本文在研究釋用方法的基礎上，進一步探究釋用模型的滾動訂正方法。

2 資料

模式資料采用EC細網格2017年1月1日—2019年6月30日每日20時（北京時，下同）再分析資料，其中2017年1月1日—12月31日為釋用模式建模樣本；2018年1月1日—12月31日為獨立釋用模式檢驗樣本；2018年1月1日—2019年6月30日為模型回歸參數滾動訂正樣本。

觀測資料為舟山嵊泗國家基準站逐時10 m極大風向風速，該站站點觀測資料經人工控制，數據完整，且具有較高的準確性和代表性。

采用雙線性插值法將EC細網格10 m風再分析產品插值到觀測站點上，站點信息見表1。

表1站點信息

3 釋用方法

3.1 站點風速高度訂正

由于風速隨高度的升高而增大，各站點在對比EC細網格10 m風資料時，首先需要進行風速的高度訂正。根據之前的研究[12]，指數律模式能較好地反映風速隨高度的變化。

指數律：

式中：u和u1分別為距地面高度z和z1處的風速；m為風速隨高度的切變指數，其值的大小即表明了風速垂直切變的強度；嵊泗基準站為草地下墊面，m取0.14。

如圖1所示，經高度訂正后，EC再分析插值風速與實況風速誤差明顯改善。

3.2 考慮地形的PP法建模

在大尺度運動中，當不考慮摩擦力和地形時，空氣質點的運動遵從地轉風規則，這是我們進行風預報的基礎。但在實際中，會有地形作用且摩擦力不為零的情況。

摩擦力方面：近地面層摩擦力來自于粗糙的地面及近地面層空氣的粘性力，而空氣粘性力主要由湍流活動引起，近地面層湍流與低層溫度層有關，即與大氣穩定度相關。由于摩擦力的存在，定量表示地面風有一定困難，難以精確估計摩擦力的大小。從實測風的讀數可見，風向和風速均存在著明顯的脈動現象，只能以自記曲線的10 min平均作為平均風，而以某一時段中最大平均風作為該時段的平均風[7]。挑選因子時應從大氣穩定度入手，尋求表示估計偏差風的統計關系式。基于以上理論和人工經驗，挑選50個與大氣穩定度有關的因子。這些因子包括4個層次（地面、850 hPa、700 hPa和500 hPa）的再分析場，即溫度、風、比濕、相對濕度、溫度平流、水汽通量散度、渦度、垂直速度、散度、位渦和位勢高度等熱力動力因子。

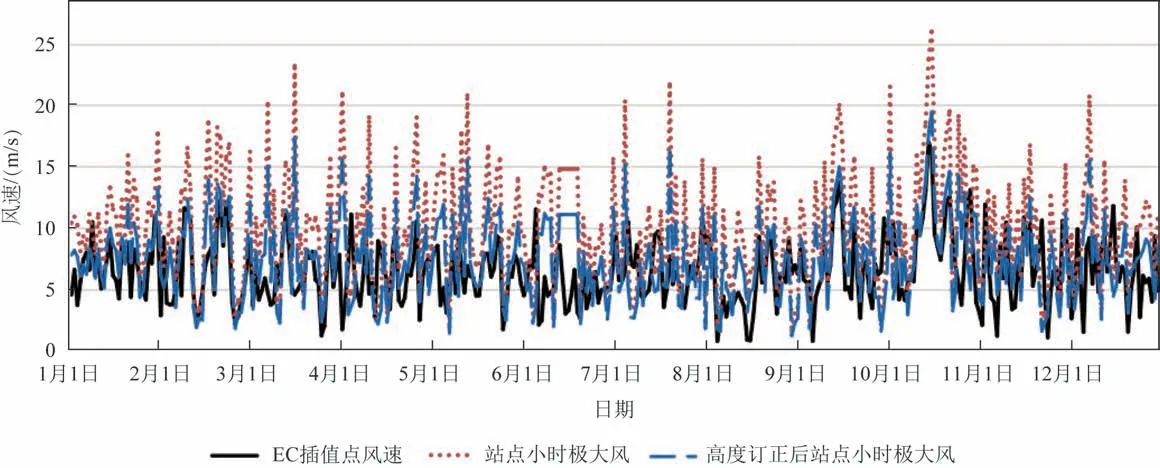
圖1 2017年1月1日—12月31日每日20時EC插值點風速、站點小時極大風和高度訂正后站點小時極大風對比

由于不同的物理量有不同量綱，需要先對各預報因子作標準化處理，本文采用正規化方法處理。應用多元線性回歸方法對2017年整年觀測和再分析標準化資料建立回歸方程。經計算，方程線性關系顯著性F=2.66，查F分布表F（50，314）的99%分位數為2，可見線性關系為顯著。計算出單個自變量顯著性t值（見表2），按0.01顯著性（t 0.99（314）=2.59）T檢驗標準對因子進行排序篩選，保留了28個相關性較大的因子，建立PP法模型。

PP法回歸方程：

YS=XSB+ε （2）

式中：YS表示站點高度訂正標準化風力；XS表示700 hPa位勢高度、850 hPa溫度、EC插值點風力和1 000 hPa相對濕度等28個標準化預報因子；B表示待估參數；ε表示隨機誤差。

地形方面：風速的大小除與水平氣壓梯度有直接關系外，與地形也有較大關系。舟山群島地形復雜，各觀測站點多有地形影響，主要包括山體阻擋使風力減小、狹管效應和爬坡使風力增大等。地形不管以哪種形式對風力產生影響，具體表現在站點風力測量都在相同氣壓梯度下，不同風向的站點風速大小不同，因此，本文采用分風向的方法，具體研究地形對站點風速的影響。

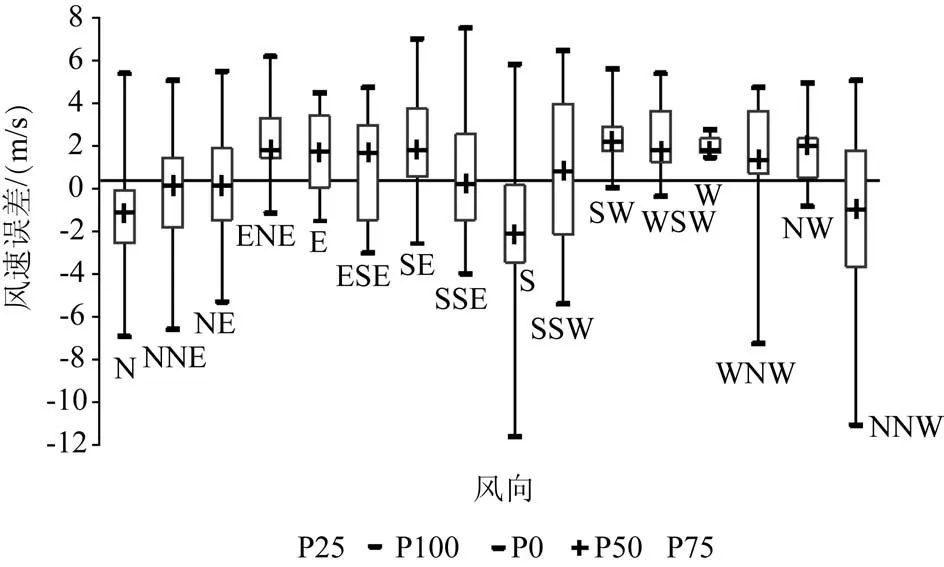
圖2 嵊泗站各風向多元回歸預報與高度訂正后風速誤差箱線圖

按16方位的風向進行研究，分別計算嵊泗站在各個風向條件下，PP法模型擬合與站點高度訂正的風速誤差。如圖2所示，我們發現擬合風速誤差和風向角度呈現較明顯的三角函數分布特征，風速誤差和風向角度兩者的相關系數高達R2=0.82。對各風向風速進行擬合，均方根誤差（Root Mean Squared Error，RMSE）為0.63，擬合效果較好（見圖3）。

故可得風速在不同風向角度的誤差公式如下：

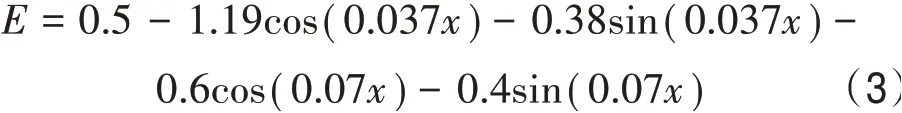
式中：E表示各風向角度下的擬合風速誤差；x為風向角度。據此建立考慮地形的PP法模型。

考慮地形的pp法回歸方程：

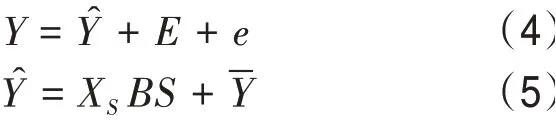
式中：Y表示站點高度訂正風力；Y?表示多元回歸預報風力；E表示各風向角度下的擬合風速偏差；e表示隨機誤差；XS表示700 hPa位勢高度、850 hPa溫度、EC插值點風力和1 000 hPa相對濕度等28個標準化預報因子；B表示待估參數；S表示Y的標準差；-Y表示Y的平均值。

圖3 嵊泗站各風向風速誤差擬合圖

4 效果檢驗

4.1 訂正誤差評價方法

本文采用統計指標參數平均絕對誤差（Mean Absolute Error，MAE）和RMSE評價模型訂正前后的風速誤差。具體公式如下：

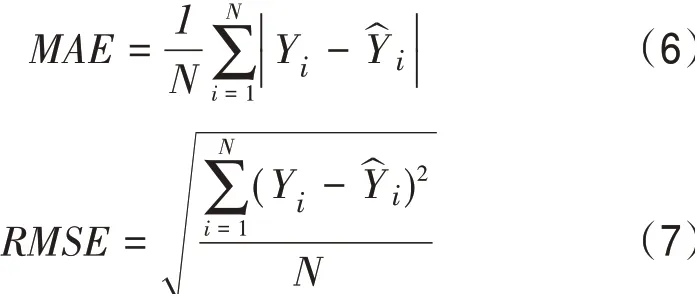
4.2 考慮地形的PP法模型檢驗

本文通過高度訂正、PP法多元線性回歸擬合和考慮地形的風力誤差訂正，對2017年嵊泗基準站高度訂正風速和EC再分析資料進行了預報建模。每經一次訂正，誤差都有改進，其中高度訂正后誤差改進最明顯，最終各項評價指標的訂正結果都超過50%，具體見表2。

利用2018年全年每日20時EC再分析資料，應用所建模型進行預報，對比嵊泗站點高度訂正后風速。如圖4所示，模型預報誤差較原始EC插值點預報誤差有較大改進，計算得出MAE為2.57，RMSE為3.27，可見模型具有較好的訂正能力。

5 卡爾曼濾波回歸系數訂正與檢驗

由于EC模式的預報性能和站點的氣候特征都在發生變化，因此模型中的回歸系數也應隨時間發生變化。本文采用卡爾曼濾波法對模型回歸系數進行滾動訂正。卡爾曼濾波是一種數學統計方法，該方法采用量測方程和狀態方程組成的線性隨機系統狀態空間模型來描述濾波器，并且利用狀態方程的遞推算法對濾波器的狀態變量做出最佳估計，從而求得濾掉噪聲的有用信號的最佳估計[13]。卡爾曼濾波一般用來處理濾波、預測和平滑3方面的問題。

天氣預報領域中的卡爾曼濾波的基本公式如下：

量測方程：

狀態方程：

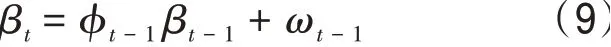
表2嵊泗站點2017年1月1日—12月31日20時高度訂正前后、多元回歸擬合后和風向修正后風速誤差對比

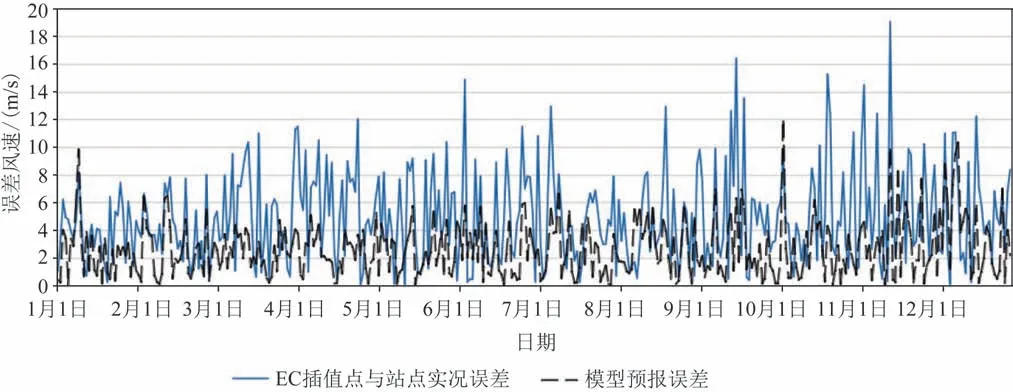
圖4 2018年1月1日—12月31日每日20時原始誤差與模型預報誤差對比

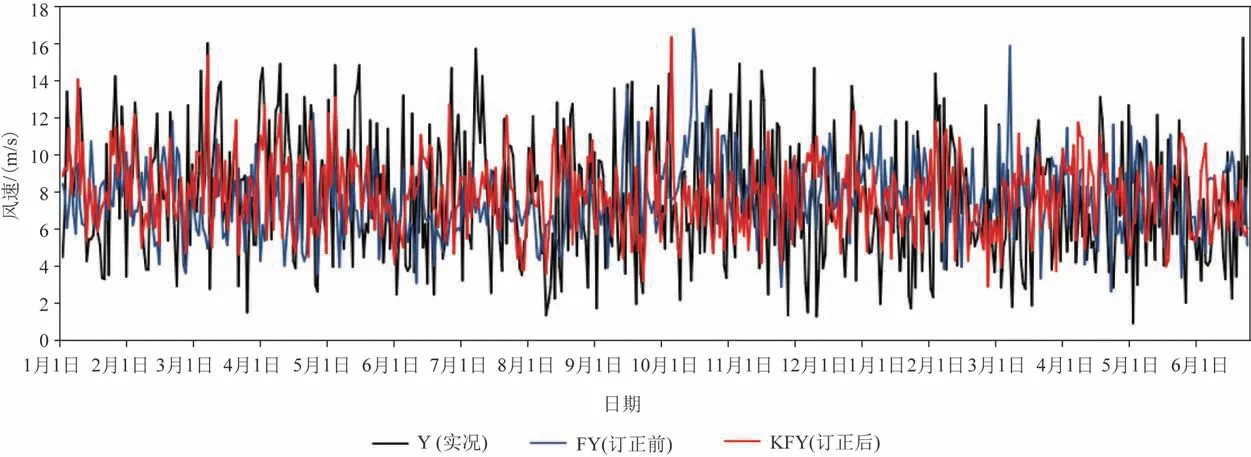
圖5 2018年1月1日—2019年6月30日每日20時卡爾曼濾波滾動訂正前后風速絕對誤差對比

6 結論

本文根據EC細網格資料和嵊泗站點實況資料，建立了考慮地形的PP法模型，用卡爾曼濾波法滾動更新回歸參數，以MAE和RMSE作為誤差訂正評價指標，得出以下結論：

（1）對風速的高度訂正，能有效降低EC細網格模式的預報誤差，MAE和RMSE由高度訂正前的4.47 m/s和5.51 m/s降至高度訂正后的2.70 m/s和3.53 m/s，誤差減幅分別為40%和36%。

（2）用PP法建立的站點高度訂正風速和EC模式10 m風場、700 hPa位勢高度和850 hPa溫度等預報因子間的多元線性回歸方程，方程線性關系顯著性F=2.66，查F分布表，F（50,314）的99%分位數為2，具有顯著的線性關系。

（3）分析各風向的擬合風速誤差，發現風速誤差與風向角度存在明顯的正余弦函數關系，擬合后相關系數R2=0.82，RMSE=0.63，擬合效果較好。

（4）經高度訂正、多元線性回歸和分風向誤差風速訂正后，MAE和RMSE由高度訂正前的4.47 m/s和5.51 m/s降至模型訂正后的2.09 m/s和2.71 m/s，誤差降幅達到53%和51%，訂正效果明顯。

（5）利用2018年全年資料進行模型訂正釋用能力檢驗。經計算，模型預報風速與站點高度訂正風速的MAE為2.57 m/s，RMSE為3.27 m/s，模型具有較強的訂正釋用能力。

（6）利用卡爾曼濾波法，實時吸收最新EC細網格資料和站點實況風速資料，滾動訂正所建模型的回歸系數，計算得出MAE和RMSE由訂正前的2.91 m/s和3.59 m/s滾動降至訂正后的2.66 m/s和3.34 m/s，可見該方法具有滾動更新能力，且能進一步提高模型訂正釋用能力。