豎凹槽內螺旋波紋管的沸騰換熱與PEC評價

王金鋒 滕文強 謝 晶 朱生林 常婉瑩

(1.上海海洋大學食品學院，上海 201306；2.上海冷鏈裝備性能與節能評價專業技術服務平臺,上海 201306；3.上海水產品加工及貯藏工程技術研究中心,上海 201306；4.上海海洋大學食品科學與工程國家級實驗教學示范中心,上海 201306)

能源產業是中國經濟的重要支柱產業，設計高效節能的換熱設備是實現能源行業可持續發展的重要舉措，而螺紋管是被廣泛應用的換熱設備。其中，兩相流的螺紋管被廣泛用于食品速凍、牛奶和果汁滅菌等工藝中，尤其是在冷卻、速凍、預熱、再熱、蒸煮加熱和廢水加熱等處理過程中應用較多[1-3]。

目前，螺紋管的研究主要集中在豎凹槽和橫螺旋波紋等結構對換熱的影響。其中，豎凹槽結構的研究主要是針對制冷劑的沸騰換熱特性。王樂樂等[4]研究發現，小管徑豎凹槽結構管內干涸現象出現較晚、臨界干度較大。戴源德等[5]使用CFD對R290在長度500 mm、外徑7 mm換熱管中兩相流沸騰進行模擬研究，由于換熱管內豎凹槽結構存在，工質在管內劇烈擾動。歐陽新萍等[6]研究表明，當流動處于層流或者層流與湍流的過渡區時，較大的螺旋角有利于換熱；當流體處于湍流時，較小的螺距會產生較多的螺紋頭數，較多的螺紋頭數更有利于換熱。

針對橫螺旋波紋結構主要是研究不同內螺旋波紋結構管的換熱特性。Córcoles等[7]研究表明，螺旋波紋高度與內管直徑之比最大和螺距與內管直徑之比最小時，內管壓降最大；螺紋高度與內管直徑之比中等和螺距最小時，內管的換熱效果最好。陳栩等[8]研究表明小齒高大齒頂角的結構有利于液態制冷劑與壁面形成均勻的液膜，促進管內的換熱過程，相同管徑下，較多的齒數有利于擾動的增強。劉希祥等[9]研究表明，32°旋轉角螺紋管最有利于換熱并且壓降損失最小。Wang等[10]模擬結果表明內管直徑的大小對二次流動的影響很小，表面換熱系數和壓降均隨內管直徑的減小而增大。

研究擬通過CFD對不同數量豎凹槽結構的內螺旋波紋管沸騰換熱特性進行模擬研究，比較豎凹槽內螺旋波紋結構管的表面換熱系數和壓降變化，并結合PEC進行評價，以期為豎凹槽內螺旋波紋管優化設計提供依據。

1 數值模擬

1.1 物理模型及網格劃分

豎凹槽內螺旋波紋管結構如圖1所示，內螺旋波紋管總長度300 mm，內管內徑5 mm，管壁0.2 mm，外管內徑8.2 mm，內螺紋高度0.3 mm，其中豎凹槽高度與內螺紋高度保持一致，豎凹槽數量為0，4，8，12，14，16，18，20。內管為內螺旋波紋結構，為了更好地對管內的流動沸騰進行捕捉，對內管壁面和外管內壁面進行邊界層處理。

圖1 內螺旋波紋管結構Figure 1 Inner spiral bellows structure

1.2 Mixture模型

兩相流模型選擇Mixture模型，此模型包含連續性方程、動量方程和能量方程。

(1) 連續性方程：

(1)

(2)

(3)

式中：

ρm——混合密度，kg/m3；

αk——第k相體積分數；

ρk——第k相密度，kg/m3；

(2) 動量方程：

(4)

式中：

βm——體積熱膨脹系數。

(5)

(6)

(3) 能量方程：

(7)

式中：

Keff——有效熱傳導率，W/(m· K)；

SE——所有相的能量源項，J。

第二相體積分數方程：

(8)

相變模型方程：

Senergy=-ML，

(9)

(10)

(11)

(12)

式中：

M——傳質速率，mol/(m2·s)；

L——汽化潛熱，J/kg；

Tref——制冷劑物性的參考溫度，℃；

Tsat——制冷劑的飽和溫度，℃。

1.3 湍流模型

湍流模型選擇RNGk—ε模型，采用標準近壁處理，其包含的方程:

(13)

(14)

式中：

h——表面換熱系數，W/(m2·K)；

μ——湍流黏度，Pa·s；

k——湍流脈動動能，J；

Gk——層流速度梯度產生的湍流動能，J；

Gb——浮力產生的湍流動能，J；

ε——湍流脈動動能耗散率；

YM——湍流擴散產生的波動；

C1、C2——常數系數。

1.4 邊界條件及算法設置

模型的邊界條件和算法設置步驟：

(1) 在兩相流Model中將R32的液相設為第1相，R32的氣相設為第2相，外管的水設為第3相，并且考慮表面應力的影響，激活Mixture模型中的“implicit body force”選項，沸騰換熱模型選擇Mixture模型中“Evaporation-Condensation”模型。

(2) 內外管進口均為速度入口，出口均為壓力出口，內管為R32液相入口，外管為水入口，其中外管進口水的體積分數為100%，R32和水的流動為順流。

(3) 內外管壁材料為銅，內外管為耦合邊界。

(4) 采用SIMPLE算法，選擇Solve N-Phase Volume Fraction Equations，能量方程、體積方程、湍流動能方程均采用一階迎風方程。

2 結果與討論

2.1 數值模擬可行性驗證

采用Liu and Winterton關聯式[11]對數值模擬結果進行驗證。沸騰換熱分為核態沸騰和膜態沸騰且存在相互作用。根據兩種沸騰換熱系數的線性加減方式，分別采用膜態沸騰強化因子E和核態沸騰弱化因子S對其進行修正。

h3=[(Eh2)2+(Sh1)2]0.5，

(15)

(16)

(17)

(18)

S=(1+0.055E0.1Re0.16)-1，

(19)

(20)

(21)

式中：

h3——表面換熱系數，W/(m2·K)；

λ——流體的導熱系數，W/(m· K)；

d——內管的當量直徑，m；

M——相對分子質量；

Q——熱流密度，W/m2；

ρ——流體密度，kg/m3；

υ——流體速度，m/s；

μ——流體黏度，Pa·s；

Cp——流體的定壓比熱容，J/(kg ·K)。

模擬值和理論值的比較結果見表1。由表1可知，模擬值與理論值的偏差保持在6%～10%，因此，采用該數值計算模型是可行的。

表1 不同數量豎凹槽內螺旋波紋管模擬值與理論值比較Table 1 Comparison of analog value and theoretical value of spiral ripple management in different number of vertical grooves

2.2 表面換熱系數

在進行內螺旋波紋管設計時，提高表面換熱系數是主要目的。如圖2所示，與光管相比，內螺旋波紋管的表面換熱系數顯著增大(147%)；豎凹槽內螺旋波紋管的表面換熱系數隨豎凹槽數量的增加先增大后減小，當豎凹槽數量為16時達最大值(157%)；隨著豎凹槽數量的進一步增加，表面換熱系數逐漸減小，當豎凹槽數量為20時，表面換熱系數為光管的154%。

圖2 豎凹槽內螺旋波紋管的表面換熱系數Figure 2 Surface heat transfer coefficient of inner spiral bellows with different number of vertical grooves

2.2.1 二次流動分析 強化管的換熱特性和管內流體流動現象顯著相關，內螺旋波紋結構可以強化管內換熱，在此基礎上，對不同數量豎凹槽內螺旋波紋管內的流動沸騰現象進行研究。如圖3中橢圓所指示區域，流體在內螺旋波紋結構下方和側方產生聚集，這種聚集導致徑向二次流動的產生[12]。隨著二次流動的產生，湍流動能(TKE)[13]顯著增加(如圖4所示)，內螺旋波紋結構下方和側方TKE明顯高于其他位置，較高TKE表明此處湍流程度較高，強化沸騰換熱強化程度較高。

圖3 豎凹槽內螺旋波紋管的速度矢量圖Figure 3 Velocity vector diagram of spiral bellows in different numbers of vertical grooves

圖4 豎凹槽內螺旋波紋管的TKE分布圖Figure 4 TKE distribution of spiral bellows in different numbers of vertical grooves

豎凹槽與內螺旋波紋結構相切割，隨著豎凹槽數量的增加，內螺旋波紋結構下方和側方的聚集慢慢增加，徑向二次流動逐漸加強，湍流程度得到加強，沸騰換熱強化程度越來越高，然而隨著豎凹槽數量的進一步增加，聚集慢慢減小，徑向二次流動逐漸減弱，湍流程度被減弱。此現象產生的原因是，相鄰兩豎凹槽間內螺旋波紋結構的弧線長度隨豎凹槽數量的增加而逐漸減小(如圖5所示)，徑向長度隨之減小，所以徑向二次流動被弱化，沸騰換熱被減弱，因此，表面換熱系數先增大后減小[14]。

圖5 豎凹槽內螺紋波紋管截面圖Figure 5 Cross section of internal screw bellows with different number of vertical grooves

2.2.2 內管壁面過熱度對氣泡的影響 內管壁面的過熱度影響內管壁面處氣泡的生成與脫離，氣泡的生成與脫離又決定內管沸騰換熱的強弱。內管(單位長度)中的內螺旋波紋結構增大了換熱表面積(如圖6所示)，同時在內螺旋波紋結構處的過熱度高于光滑壁面，由克勞修斯—克拉貝龍方程[15]可知，內螺紋波紋結構處更容易形成汽化核心，而氣泡的生成與脫離又強化了管內沸騰換熱。

圖6 豎凹槽數量14時內螺旋波紋管中溫度分布圖Figure 6 Temperature distribution in inner spiral bellows with 14 vertical grooves

豎凹槽與內螺旋波紋結構相切割，換熱表面積隨之增加，氣泡生成和脫離的表面積也隨之增加，沸騰換熱得到強化。隨著豎凹槽數量的進一步增加，內管表面努塞爾數逐漸減小(如表2所示)，內管沸騰換熱效果反而降低(如圖7所示)，是因為套管結構單位時間內外管進水量相同，熱量的傳遞集中于內螺旋波紋管的內壁面附近，換熱表面積的過度增加導致部分內螺紋結構處的溫度有所下降(如圖8所示)，其過熱度低于氣泡脫離壁面所需的過熱度，氣泡無法脫離壁面從而弱化內壁面處沸騰換熱，因此，內螺旋波紋管的表面換熱系數先增大后減小[16]。

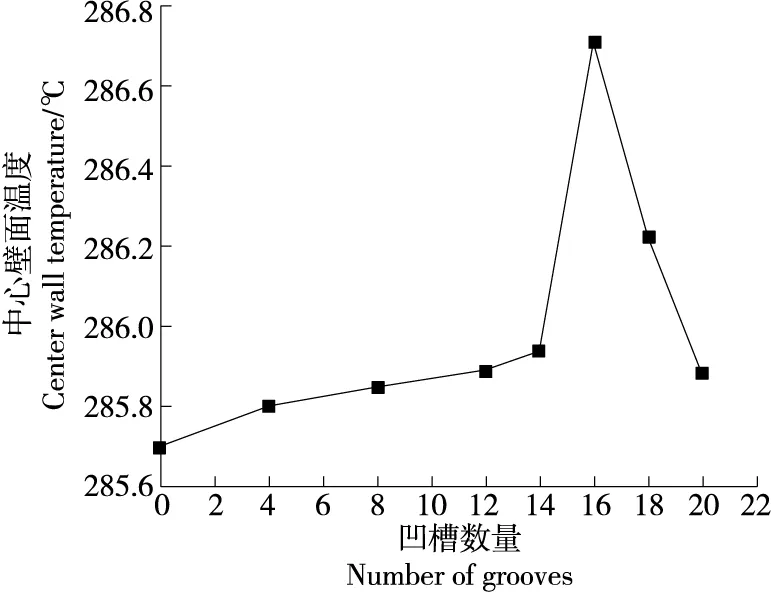
圖8 豎凹槽內螺旋波紋管中心壁面溫度Figure 8 Central wall temperature of inner spiral bellows with different number of vertical grooves

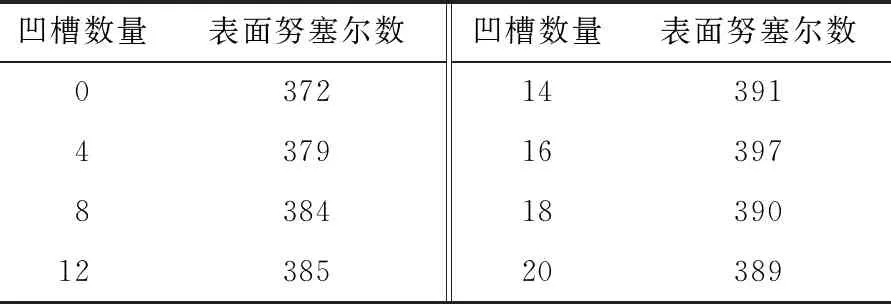
表2 豎凹槽內螺旋波紋管的表面努塞爾數Table 2 Surface Nusselt numbers of spiral bellows in different numbers of vertical grooves

圖7 豎凹槽內螺旋波紋管的R32-vapor分布圖Figure 7 R32-vapor distribution of spiral bellows in different numbers of vertical grooves

2.3 壓降分析

在進行內螺旋波紋管設計時，較高的內管壓降會增加壓力損失。由圖9可知，當豎凹槽數量為0時，內螺旋波紋管壓降為光管的221%，內管壓降隨豎凹槽數量的增加先增大后減小，當豎凹槽數量為16時達最大，為光管壓降的261%，豎凹槽數量的進一步增加，內管壓降明顯下降，當豎凹槽數量20時，內管壓降為光管的233%。

圖9 豎凹槽內螺旋波紋管的內管壓降Figure 9 Pressure drop of inner spiral bellows with different number of vertical grooves

由圖3可知，內螺旋波紋結構增大了內管流體的環流面積，流體在內螺旋波紋管下方的聚集產生了徑向二次流動，此外，內螺旋波紋結構側方有流體聚集(如圖3中紅色橢圓區域)，增大了內管壓降。

豎凹槽與內螺旋波紋結構相切割，隨著豎凹槽數量的增加，內螺旋結構下方的聚集慢慢增強，側方的聚集逐漸形成漩渦(如圖3中紅色橢圓區域)，內管壓降得到增強，當豎凹槽數量為16時，內螺旋波紋管的內管壓降增加最迅速，壓力最大(如圖10所示)。隨著豎凹槽數量的進一步增加，相鄰豎凹槽間內螺旋波紋結構的弧線長度變短(如圖5所示)，聚集效應慢慢減弱，漩渦逐漸消失，湍流流動被破壞，環形流動被減弱，內管壓降逐漸下降[17-19]。

圖10 豎凹槽內螺旋波紋管的內管壓降Figure 10 Pressure drop of inner spiral bellows with different number of vertical grooves

2.4 性能評估

PEC[20]是一種性能評價標準方法，定義為豎凹槽內螺旋波紋管的強化效果與泵功率損耗的比值，其值決定表面換熱系數和壓降的關系。

(22)

式中：

PEC——PEC值；

UC——帶波紋管的雙管熱交換器的總傳熱系數，W/(m2·K)；

US——具有光滑管的雙管熱交換器的總傳熱系數，W/(m2·K)；

ΔPC——內波紋管中雙管熱交換器壓降，Pa；

ΔPAC——波紋管一側的波紋管雙管換熱器壓降，Pa；

ΔPS——內光滑管上的雙管熱交換器壓降，Pa；

ΔPAS——圓環側帶有光滑管的雙管熱交換器壓降，Pa。

表3為不同內螺旋波紋結構下的PEC數值，所有的豎凹槽內螺旋波紋結構中PEC均>1，其中豎凹槽數量為16時，PEC為最大值(1.523)，所以在內管內徑5 mm，外管內徑8.2 mm，管壁0.2 mm，內螺旋波紋高度0.3 mm，豎凹槽數量為16時，豎凹槽內螺旋波紋管強化換熱性能最優。

表3 不同豎凹槽數量下內螺旋波紋管的PECTable 3 PEC of inner spiral bellows with different number of grooves

3 結論

以套管結構為設計模型，采用CFD對不同豎凹槽數量的內螺旋波紋管進行沸騰換熱模擬研究，分析比較內螺旋波紋管的表面換熱系數和內管壓降，結合PEC評價，優化豎凹槽內螺旋波紋管結構。結果表明，內螺旋波紋結構增大了內管的換熱表面積和環流面積(單位長度)，且產生徑向二次流動；表面換熱系數和壓降分別提高至光管的147%，207%；與內螺旋波紋管相比，豎凹槽內螺旋波紋管表面換熱系數和壓降均隨豎凹槽數量的增加先增大后減小，當豎凹槽數量為16時達到最大值，分別為內螺旋波紋管的107%，118%；此外，當豎凹槽數量為16時，PEC最大(1.523)，此時換熱管的綜合性能最優。在內(外)管內徑分別為5.0，8.2 mm，內(外)管壁厚度為0.2 mm 和內螺紋高度0.3 mm下，豎凹槽數量為16的豎凹槽內螺旋波紋管的換熱性能最佳，但是不同管徑下豎凹槽內螺旋波紋管性能最優化結構以及豎凹槽與豎凹槽內螺旋波紋管的性能關系還有待進一步研究。