基于ReliefF-SFA的熱處理爐過程監測方法

王偉兵

河鋼股份有限公司邯鄲分公司信息自動化部，河北 邯鄲 056000

隨著科學技術的發展，現代工業系統的規模和復雜程度也日益增加。熱處理爐設備[1]在退火過程中有著十分重要的地位，其運行狀態對產品質量產生了直接的影響。因此，對常化爐的運行過程監測方法的研究顯得十分重要。多元統計的方法[2]是目前較為常用的過程監測方法，慢特征分析（SFA）作為一種全新的特征提取和降維方法，近年來受到了廣泛關注。它能夠從時序信號中提取出變化最緩慢的成分，有效表征系統所固有的本質屬性，這些成分被稱為慢特征。然而傳統的SFA只是對數據做了一個映射變換，并不能實現數據的降維，在實際的熱處理設備工業背景下，生產過程復雜，數據變量少則數十個，多則上千個。即使變量維度不大，如果盲目地放入算法中，將不能保證監測的有效性，可能會出現漏報或誤報的現象，對于熱處理爐的過程監測存在一定的挑戰性。

在SFA方法的基礎上，文章提出了ReliefF-SFA方法，將原有方法進行擴展，先對數據進行映射變換得到慢特征；然后采用ReliefF方法選取權重大的變量放入主子空間，其余的放入殘余子空間，使其能夠判斷是否發生故障。

1 慢特征分析概述

慢特征分析（SFA）是Wiskott[3]提出的一種從快速變化的時序信號中提取不變或慢變特征的方法，它作為一種新的特征提取方法受到廣泛關注。慢特征表征了數據所屬事物的固有性質，在時序信號的分析中發揮了重要的作用，其通過將主元分析應用于輸入信號的白化和白化后信號的一階時間導數，從而提取出一組按時間慢度從小到大排列的不相關特征。因此，慢特征分析具有挖掘工業過程真實情況的潛力，其詳細步驟可參照文獻[4-5]。

2 ReliefF算法原理

FReliefF算法是基于Relief算法[6-7]的一種特征選擇算法，Relief作為經典的特征權重算法，根據各個特征與類別的相關性賦予各個特征權重，但是其缺點是局限于處理二分類問題。

ReliefF算法應用于多類問題，需要每次從樣本訓練集里面隨機抽取某一樣本D，然后從同于D類的樣本集中選出D的k個近鄰樣本，從每個不同于D類的樣本集中均選出k個近鄰樣本，接著特征權重全部更新，其表達如下式：

式中：diff(A,Ri,Rj)為樣本Ri和樣本Rj在特征A上的差，其計算公式為Mj(C)，表示C中的第j個最鄰近樣本。其表達如下式：

相關學者在Relief基礎上提出了ReliefF算法，從而解決了多分類問題。ReliefF的偽代碼如下所述。

3 ReliefF-SFA分析方法

通過對SFA算法的分析可知，它只是完成了一次投影變換，使得輸出代表了原數據最本質的特征，然而其無法去除數據冗余特征。ReliefF算法能計算出每個特征的權重值，將對分類起到積極作用的特征權重予以保留，從而實現數據的降維。文章提出ReliefF-SFA的方法，基本思路是通過慢特征分析將正常工況下的數據和故障數據轉換成對應的慢特征，并給這些不同類的特征打上標簽，作為ReliefF算法的輸入，再通過ReliefF算法，計算出每個特征的權重值，該特征權重越大，則該特征的分類能力越強。最后通過設置閾值，篩選出對故障識別能力強的特征放進主子空間中，將對故障識別能力弱的特征放進殘差空間中。

3.1 ReliefF-SFA算法步驟

（1）對m維輸入向量進行中心標準化得到x(t)。

（2）輸入矩陣進行白化：z(t) =S(x(t))，矩陣S是白化矩陣，可由對x(t)進行主成分分析確定。

且λ1≤λ2≤...≤λJ，則輸出信號如下：

（4）通過公式（1）將正常工況下的數據和故障數據轉換成對應的慢特征，并給這些不同類的特征打上標簽，作為ReliefF算法的訓練樣本集。

（5）設置ReliefF算法中樣本抽樣次數為c，近鄰點個數設置為k，并將所有特征的權重值置0。

（6）執行c次循環，每次循環執行以下步驟：①在特征yj的樣本集中隨機選擇一個樣本R。②從同類樣本中找到k個最近鄰樣本Hj，從每個不同類（C≠class（R））樣本中都找到k個最近鄰樣本Mj。③循環計算R的m個不同特征的權值（yj為其中某一個特征）：

式中：yj為某一個特征；W(yj)為特征權重；diff (yj,Ri,Hj)為樣本R與近鄰樣本Hj在第yj個特征上的距離；p(C)為類的分布概率。

（7）計算出所有的特征權重后，采取貢獻率的方法設置閾值δ，若W(yj)>δ，則放入主子空間Y中，其余的放入殘余空間Ye中。

3.2 基于ReliefF-SFA的試驗結果

針對熱處理爐工作過程，文章主要選取了常化爐的入口溫度、輻射管的溫度、風機電流等36個變量作為主要監測的過程數據；按照5s的間距取，一共形成1500組正常數據。利用正常的1000組數據對慢特征分析進行建模，轉變成1000個慢特征，并標記為類型0。經查閱，歷史故障數據集一共有兩種故障：第一種故障是加熱一區的傳感器測量值偏移故障；第二種故障是加熱三區的傳感器測量值偏移故障。

從這兩種故障中提取1000組數據，轉變成慢特征并標記為類型1、類型2。將1000組正常數據對應的慢特征和這兩種故障數據對應的慢特征組成3000×36的數據矩陣，作為ReliefF算法的輸入，設置ReliefF算法中的k值為10。其得到的36個特征權重數值按順序排列后如圖1所示。按照貢獻率的原則，確定閾值為0.01，即權重大于0.01的放入主子空間（共27個），其余放入殘余空間。

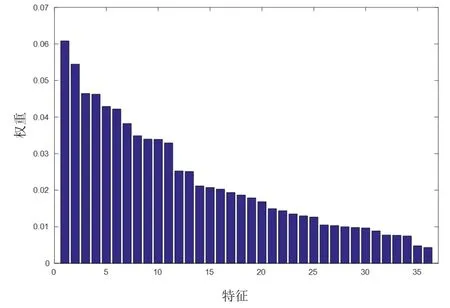
圖1 不同特征權重柱狀圖

為了驗證基于ReliefF-SFA方法過程監測的有效性，文章將ReliefF-SFA算法與SFA算法進行比較，并通過監測氣墊爐運行過程來驗證該方法的有效性。該數據是從某生產線上以5s為間隔采集的數據，包括正常數據1500個（1000個用于建模，500個用于測試）。控制限為98%的置信度，如果統計量的值超過控制限，則表示發生了故障；如果統計量的值沒有超過控制限，則表示系統正常運行。在該試驗中，在第50個數據后引入故障，兩種方法的故障檢測率如表1所示。以故障2為例，ReliefF-SFA與SFA算法的比較如圖2、圖3所示。

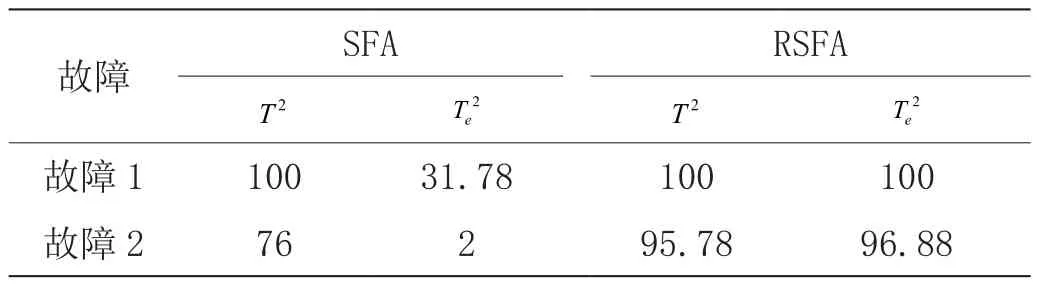
表1 SFA和RSFA的故障檢測率

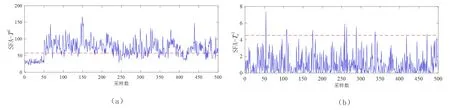
圖2 SFA在故障2下的監測效果圖

圖3 ReliefF-SFA在故障2下的監測效果圖

從圖2、圖3中可以看出，ReliefF-SFA方法比SFA方法能更好地檢測出故障，在前50個點中，兩種方法的統計量都位于控制限之下，即都是正常數據。然而在SFA中，第50個點后的統計量不全超過控制限，存在漏報的問題，通過比較，ReliefF-SFA在兩個子空間能很好地檢測出故障。

4 結束語

文章針對慢特征分析方法不能降維的問題，提出一種基于ReliefF-SFA慢特征分析的過程監測方法，首先對數據進行投影變換，得到了慢特征；然后將正常和故障數據的慢特征放入ReliefF算法中，選取了對故障識別能力強的一些特征，實現了維度的下降。