基于全量流動理論的管材彎曲過程失穩分析研究

車移，詹紅，屈俊岑，林軍

基于全量流動理論的管材彎曲過程失穩分析研究

車移1，詹紅2，屈俊岑2，林軍2

（1. 中航工業成都飛機工業（集團）有限責任公司，成都 610073； 2. 西南技術工程研究所，重慶 400039）

基于全量流動理論，研究管材彎曲成形過程中的外側破裂和內側起皺，分析其產生的原因及控制方法。采用理論解析方法，建立了管材彎曲變形應力、應變計算公式，推導管材外側破裂和內側起皺發生的判據，并試驗驗證了預測公式的可靠性。基于推導的應力、應變計算公式，依據臨界許用變形程度，建立了管材外側破裂判據；采用能量準則，提出了管材彎曲過程起皺發生公式，確定了起皺失穩計算公式的各個邊界參數。試驗與理論結果表明，構建的最小壁厚下許用/（彎曲半徑與管材平均半徑的比值）計算公式、基于起皺失穩計算的許用/（彎曲半徑與管材平均半徑的比值）計算公式均有較高精度，可用于指導彎管工藝參數設計與優化。

管材彎曲；臨界變形；能量法；破裂；起皺

彎管類構件與通過轉接頭連接直管的組合型構件相比，具有質量小、體積小的特點，在航天、航空、航海、汽車、石油化工等領域的裝備研制中得到了大量的應用[1]。管材彎曲成形是將直管坯彎成具有一定彎曲半徑、一定彎曲角度和形狀的塑性變形方法，是彎管類構件制備的關鍵工序。近年來，隨著新一代裝備對輕量化的要求越來越高，要求彎管類構件具有壁厚小、直徑大、彎曲半徑小和尺寸精度高的特點，這也使得彎管成形技術成為先進塑性加工技術的一個重要方向。

管材彎曲成形是一個多因素作用下的塑性變形過程，該過程極有可能產生多種塑性失穩缺陷[2]。在薄壁管彎曲成形工藝中，管材外側的破裂和內側的起皺是成形缺陷中最為常見的失穩缺陷，這使得對失穩缺陷的預測和控制成為管材彎曲成形研究中的關鍵性問題之一。在2000年之前，主要采用設計人員的經驗[3]或理論計算方法[4—5]預測管材彎曲過程的壁厚變化和起皺規律并優化工藝；之后，隨著計算機技術的迅速發展，數值模擬技術成為了預測管材壁厚變化和起皺規律的主要工具，其模擬精度滿足了工藝參數優化的要求[6—11]。然而，采用數值模擬優化管材彎曲成形工藝參數，需要確定初始參數范圍，這個范圍一般依賴于工藝設計人員的經驗或者依賴于理論計算結果。管材彎曲工藝參數的計算方法一般分為兩類：一類是基于應力分析的方法[4]；二是基于應變分析的方法[5]。已有研究人員指出了這兩種方法都有相應的預測缺陷[12—14]，尤其是在確定應變分量之間的關系時，一是假設周向應變為0（即平面應變關系），二是設定厚度方向的應變為軸向應變的0.75（三向應變關系），而忽略了分量之間依賴于塑性流動規律的原理。

文中基于塑性流動方法，提出計算管材彎曲過程的應力、應變計算新方法，在此基礎上，依據能量準則，提出預測彎曲過程起皺發生公式，研究管材彎曲成形中起皺發生的影響機制，為管材彎曲成形過程的工藝參數的確定和優化創造條件，以提高彎管構件的質量，縮短工藝開發周期，降低成本。

1 管材彎曲成形過程的應力、應變分析

圖1為管材彎曲過程的任意一瞬間的剖視圖，面為彎曲的對稱面，在幾何面上的任意一點的應力與幾何關系如圖1所示，圖中：為彎曲半徑，為管材平均半徑；σ為管材圓周方向的應力；σ為方向的應力。假定徑向應力σ=0，那么基于力平衡關系，在面上任意一點的周向應力與軸向（方向）應力的關系可以寫為：

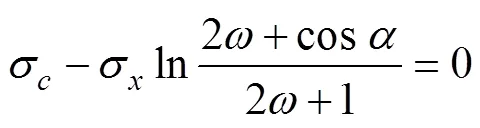
式中：；為無軸向外力作用下的軸向應力；彎曲Px為管材軸向壓（拉）力；正負號分別表示拉力和壓力；t0為管材厚度；α∈[0，π]，在[0，π/2]范圍內為管材外側，在[π/2，π]范圍內為管材內側；令。

假定管材在自由彎曲成形過程未承受軸向壓（拉）力，那么圖1的截面上任意一點沿方向（一般稱為軸向或長度方向）的應變為：

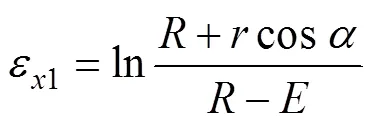
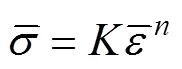
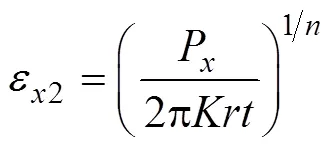
那么管材受軸向壓（拉）力作用下，方向的應變為：

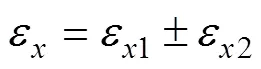
式中：正號代表管材承受軸向拉力；負號代表軸向壓力。

2 管材塑性彎曲過程的應力與應變求解

在圖1中，基于J2流動理論[15]，管材彎曲過程屈服公式可以寫為：

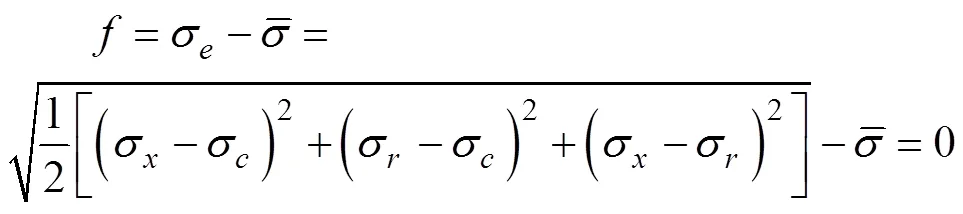
由塑性變形流動理論[15]得知：

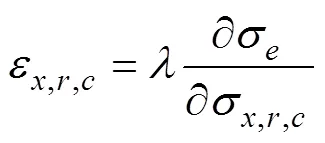
依據式（4）可得：

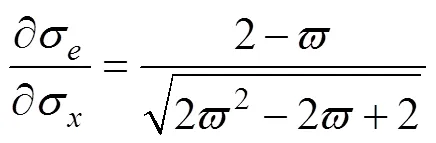
依據式（7）可以得到3個方向應變的比例關系為：

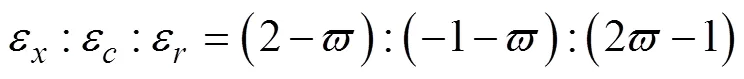
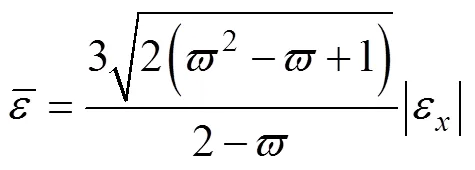
假定管材材料的塑性流動方程滿足SWIFT方程，即：

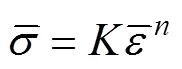
式中：為強化因子，為強化指數。

聯立式（5）、（9）、(10)，可求解出管材彎曲過程的向應力σ：

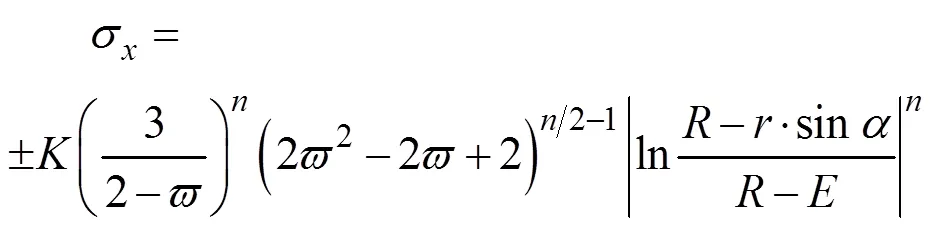
式中：正號為管材中心層外側；負號為管材中心層內側。

周向應力σ可以依據式（12）計算：

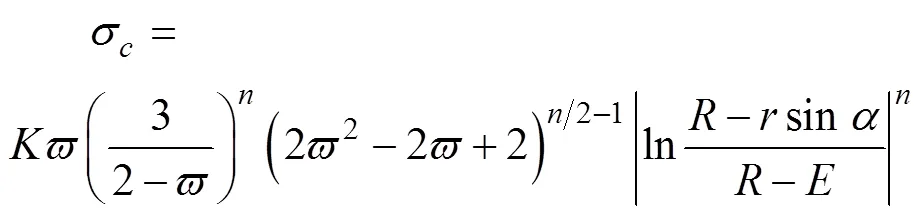
3 彎曲成形的允許變形程度與分析

基于管材彎曲過程的應力與應變計算公式，可以用于計算管材的彎曲成形極限。管材彎曲成形極限包括最外側的破裂極限和內側的失穩起皺。如果對彎曲后的管材有壁厚要求，則最外側的破裂極限可以轉為最小壁厚的控制。

3.1 管材彎曲過程的壁厚變化與許用R/r參數

管材依據式（8），可以得到管材彎曲后的徑向應變（也為厚向應變）為：

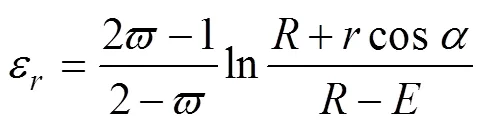
依據式（13）并結合中心層偏移計算公式，可以得出式（13）的另外一個表達式：

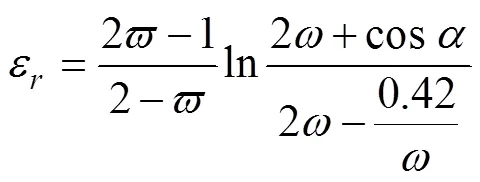
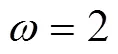
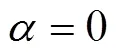
如果要求彎曲后的管材不破裂，那么許用的彎曲極限為：

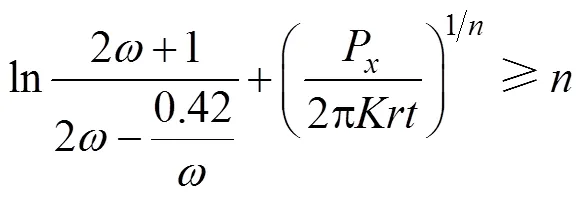
如果最小壁厚要求為min，那么許用的彎曲極限為：

基于式（15—16），采用簡單的數值求解方法，即可得最小的/計算區間。

3.2 管材彎曲過程的失穩起皺與許用R/r與r/t參數

在彎曲過程中，管材內側起皺是彎管工藝的一個主要缺陷。在彎管成形過程中，管材處于塑性穩定狀態的條件是外力做功Δ小于材料內部能量Δ。當外力做功增量Δ大于材料內部能量Δ時，管材失穩，即彎曲失穩的判據為：

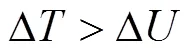
在彎曲過程中，管材起皺區域如圖2所示。假定內側因壓縮起皺形成波紋的幾何公式為：

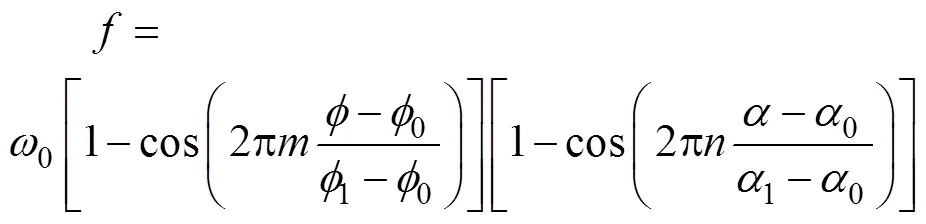
依據圖2，式（17）的邊界條件是：

在起皺的瞬間，外力做功增量和內能增量分別為：

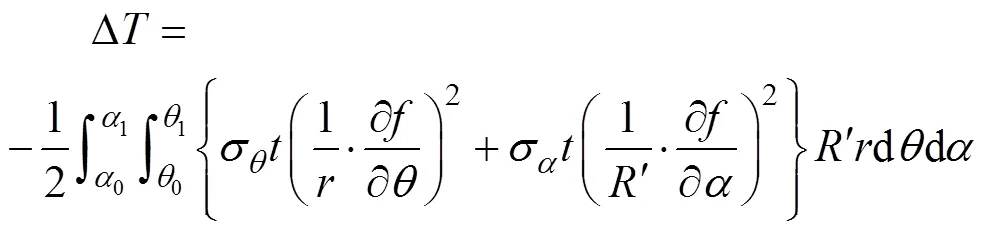
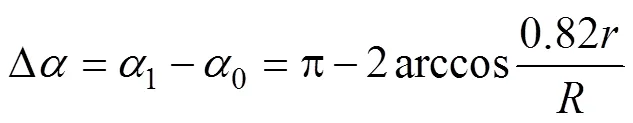
在彎曲過程的某一瞬間，管材起皺區能量總方程為：

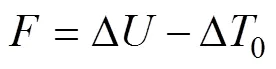
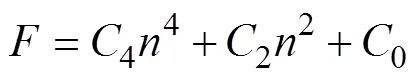
其中：

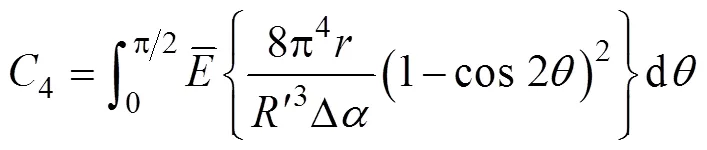
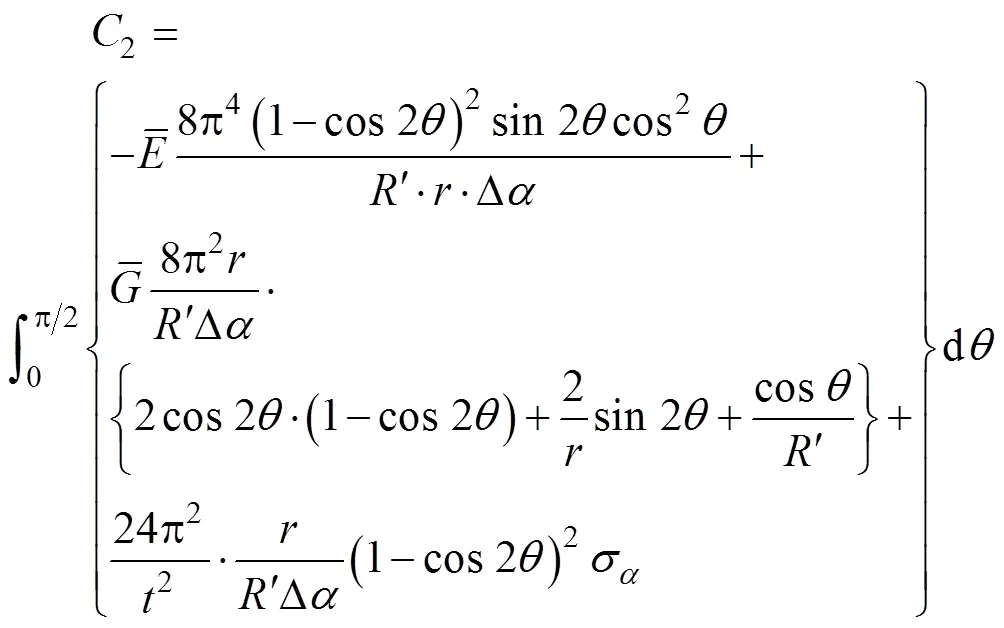
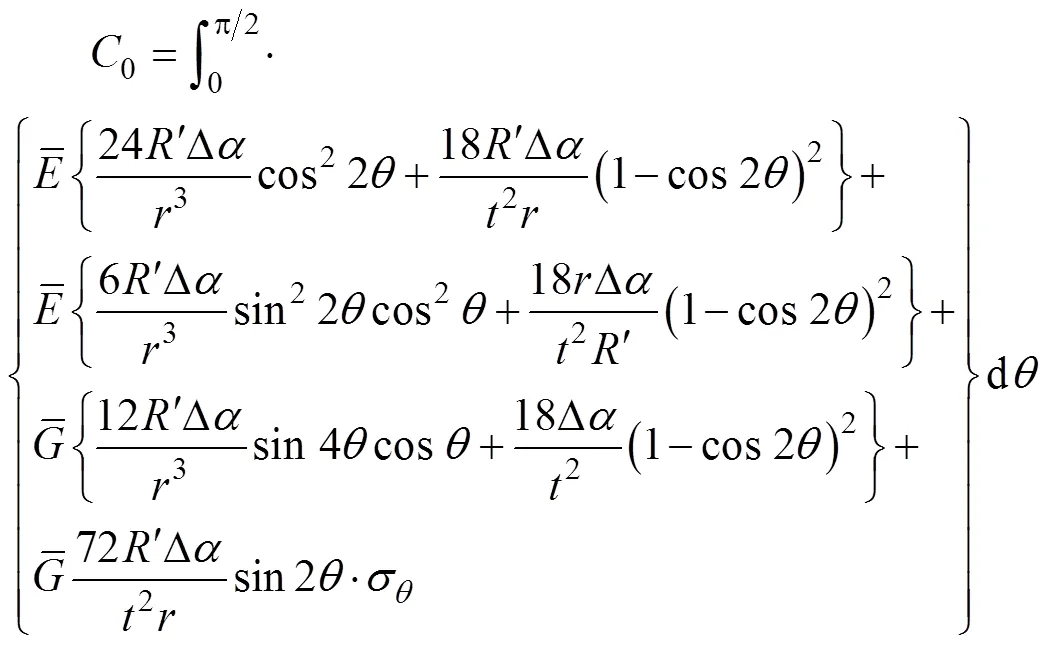
如果圖2b的截面起皺區存在，即要求式（24）有實數解，可以得到：

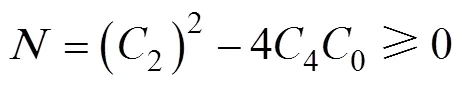
在滿足式（28）的條件下，得到臨界波數目為：

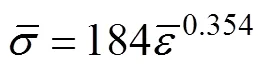
圖3 試驗與理論計算結果對比

4 結論

1）基于全量塑性流動理論，建立了管材彎曲成形過程的應力、應變計算新公式；進而構建了管材彎曲過程中最小壁厚下的許用/計算公式，同時建立了起皺失穩計算公式，確定了起皺失穩計算公式各個邊界參數。

2）試驗與理論解析結果表明，構建的最小壁厚下的許用/計算公式、基于起皺失穩計算的許用/計算公式均有較高精度，可為實際工業生產中彎曲成形工藝參數快速優化提供可靠精確的模型。

[1] CHEN Ji-sheng, E Da-xin, ZHANG Jing-wen. Effects of Process Parameters on Wrinkling of Thin-walled Circular Tube under Rotary Draw Bending[J]. The International Journal of Advanced Manufacturing Technology, 2013, 68(5/6/7/8): 1505—1516.

[2] 王同海. 管材塑性加工技術[M]. 北京: 機械工業出版社, 1998: 187—192. WANG Tong-hai. Tube Plastic Processing Technology[M]. Beijing: China Machine Press, 1998: 187— 192.

[3] 王孝培. 沖壓手冊(第2版)[M]. 北京: 機械工業出版社, 2004: 51—55. WANG Xiao-pei. Stamping Manual (2ndEdition)[M]. Beijing: China Machine Press, 2004: 51—55.

[4] STACHOWICZ F. Bending with Upsetting of Copper Tube Elbows[J]. Journal of Materials Processing Technology, 2000, 100: 236—240.

[5] TANG N C. Plastic-Deformation Analysis in Tube Bending[J]. International Journal of Pressure Vessels and Piping, 2000, 77: 751—759.

[6] 張敬文, 鄂大辛, 李延民, 等. 彎曲速度對彎管壁厚變化的影響[J]. 精密成形工程, 2012, 4(1): 35—39. ZHANG Jing-wen, E Da-xin, LI Yan-min, et al. Effects of Bending Velocity on the Change of Wall Thickness in Tube Bending[J]. Journal of Netshape forming Engineering, 2012, 4(1): 35—39.

[7] 林芳, 鄂大辛, 張敬文. 單元類型對有限元計算彎管截面畸變及壁厚變化的影響[J]. 精密成形工程, 2012, 4(3): 10—13. LIN Fang, E Da-xin, ZHANG Jing-wen. Effects of Element Types on Cross Sectional Distortion and Wall Thickness Variation in Finite Element Simulation[J]. Journal of Netshape forming Engineering, 2012, 4(3): 10—13.

[8] 樊子天, 鄂大辛, 陳吉生. 材料性能和相對壁厚對管材助推彎曲影響的分析[J]. 精密成形工程, 2013, 5(2): 16—19. FAN Zi-tian, E Da-xin, CHEN Ji-sheng. Analysis of the Influence of Material Properties and Relative Wall Thickness in Boosting Bending Process of Metal Tubes[J]. Journal of Netshape forming Engineering, 2013, 5(2): 16—19.

[9] 張敬文, 鄂大辛, 李延民, 等. 彎模間隙對5A06管彎曲橫截面畸變及壁厚變化的影響[J]. 精密成形工程, 2012, 4(2): 19—22. ZHANG Jing-wen, E Da-xin, Li Yan-min, et al. Effects of Clearance on Cross Sectional Distortion and Wall Thickness Variation of 5A06 Tube[J]. Journal of Netshape forming Engineering, 2012, 4(2): 19—22.

[10] 戴莉, 方軍, 程璐, 等. 材料參數對高強不銹鋼管數控繞彎成形失穩起皺的影響[J]. 精密成形工程, 2017, 9(1): 91—95. DAI Li, FANG Jun, CHENG Lu, et al. Effects of Material Parameters on Wrinkling of High-Strength Stainless Steel Tube in Numerical Control Rotary Draw Bending[J]. Journal of Netshape forming Engineering, 2017, 9(1): 91—95.

[11] 魏文斌, 程旋, 余耀暉, 等. 基于自由彎曲技術的6061鋁合金管的彎曲成形性能研究[J]. 精密成形工程, 2018, 10(4): 28—34. WEI Wen-bin, CHENG Xuan, YU Yao-hui, et al. Study on Bending Formability of 6061 Aluminum Alloy Tube Based on Free Bending Technology[J]. Journal of Netshape forming Engineering, 2018, 10(4): 28—34.

[12] 林艷. 薄壁管數控彎曲成形過程失穩起皺的數值模擬研究[D]. 西安: 西北工業大學, 2003: 78—83. LIN Yan. Numerical Simulation of Buckling during NC Bending of Thin-Walled Tubes[D]. Xi'an: Northwestern Polytechnical University, 2003: 78—83.

[13] 李恒. 薄壁管數控彎曲成形過程失穩起皺及成形極限的研究[D]. 西安: 西北工業大學, 2004: 154—160.LI Heng. Study on Instability and Wrinkle and Forming Limit in NC Bending Process of Thin Walled Tube[D]. Xi'an: Northwestern Polytechnical University, 2004: 154—160.

[14] YANG He, LIN Yan. Wrinkling Analysis for Forming Limit of Tube Bending Processes[J]. Journal of Materials Processing Technology, 2004, 152(3): 363—369.

[15] 俞漢清, 陳金德. 金屬塑性成形原理[M]. 北京: 機械工業出版社, 1999: 42—45. YU Han-qing, CHEN Jin-de. The Principle of Metal Plastic Forming[M]. Beijing: China Machine Press, 1999: 42—45.

[16] WANG Xi, CAO Jian. Wrinkling Limit in Tube Bending[J]. Journal of Engineering Materials and Technology, 2001, 123(4): 430—435.

Analysis on Instability in Tube Bending Process Based on Total Theory of Plasticity

CHE Yi1, ZHAN Hong2, QU Jun-cen2, LIN Jun2

(1. AVIC Chengdu Aircraft Industry (Group) Co., Ltd., Chengdu 610073, China; 2. Southwest Technology and Engineering Research Institute, Chongqing 400039, China)

Based on the total theory of plasticity, the purpose of this paper is to study the outer side cracking and inner side wrinkling in the tube bending process, and analyze the causes and control methods. In this paper, the theoretical analysis method is used to establish the calculation formula of stress and strain of tube bending deformation, deduce the criterion of tube outer cracking and inner wrinkling, and verify the reliability of the prediction formula by experiment. Finally, based on the derived stress and strain calculation formula, according to the critical allowable deformation degree, the cracking criterion of the outer side of tube is established; based on the energy criterion, the formula of wrinkling in tube bending process is proposed, and the boundary parameters of wrinkling (instability) formula are determined. The experimental and theoretical results show that the calculation formulas of allowable/(ratio of bending radius to average radius of tube) under minimum wall thickness and allowable/(ratio of bending radius to average radius of tube) based on wrinkling (instability) calculation have high accuracy, which can be used to guide the design and optimization of tube-bending process parameters.KEY WORDS: tube bending; critical deformation; energy method; cracking; wrinkling

10.3969/j.issn.1674-6457.2021.03.013

TG386

A

1674-6457(2021)03-0112-06

2021-04-09

車移（1992—），男，工程師，主要研究方向為先進制造。

詹紅（1992—），女，碩士，工程師，主要研究方向為精確塑性成形。