水下串聯立管渦激振動特性分析
劉 野 王杰文 左繼澤 李 鑫 余雄飛
(1.海洋石油工程股份有限公司,天津 300000;2.深圳海油工程水下技術有限公司,廣東 深圳 518067)
0 引言
隨著世界各國對海洋探索的不斷深入,深水油氣藏資源成為各國爭奪資源的主戰場。在水下油氣的開采項目中,立管鋪設是極為關鍵的一部分,它主要負責連接水上組塊平臺和水下井口,并完成采出液的運輸工作[1]。由于立管在水下容易受到風速、浪高和流速的共同作用,因此它會發生振動,嚴重時會導致立管管體發生疲勞受損甚至破壞。當立管受到外界流體的沖擊時,在管道流體內部會產生漩渦,當釋放的漩渦對立管施加力的頻率與立管的固有頻率相接近時,管道會發生共振現象,從而導致結構振動響應增大。在建設水下油氣田的工程中,多立管組合形式的立管群被廣泛應用,串聯、并聯等多種組合形式的立管群大大減少了施工時間,更有利于后續的管理和維護。立管群中的立管尾流會產生相互作用,立管管壁會發生多變且隨機的振動,這種現象會加速結構的機械損壞,嚴重縮短立管的使用壽命[2]。
該文將ANSYS作為模擬軟件,針對串聯立管的管道內渦激振動進行數值模擬,分析在不同頂部約束條件下,結構的振動響應和結構參數的變化。
1 數學模型
ANSYS進行流體流動模擬時遵循三大守恒定律,根據求解問題的不同,需要選擇合適的組分守恒定律與湍流方程。因為進行雙向流固耦合要對結構進行計算,所以模擬時還需要滿足動力學基本控制方程。
1.1 控制方程
1.1.1 質量守恒方程
質量守恒方程的微分方程如公式(1)所示[3]。
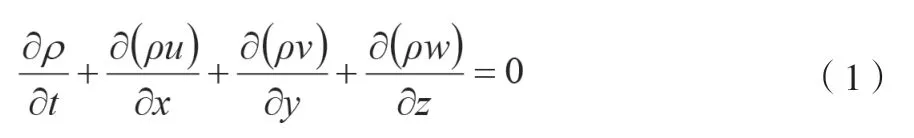
引入矢量符號
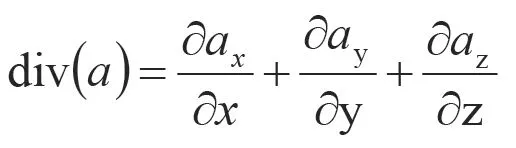
公式(1)可以寫成如公式(2)所示。

式中:ρ為密度;t為時間;u、v和w為速度矢量u在x、y、z方向上的分量。
1.1.2 動量守恒方程
動量守恒方程如公式(3)~公式(5)所 示。
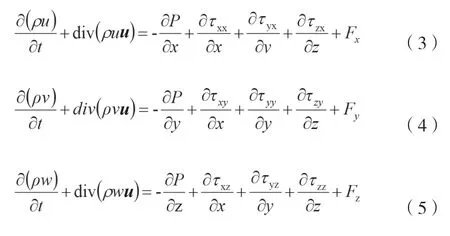
式中:P為流體微元體上的壓力;τxx、τxy和τxz為因分子黏性作用而產生的作用在微元體表面上的黏性應力τ的分量;Fx、Fy和Fz為微元體上的體力,如果體力只有重力,且在z軸向上,那么就有Fx=0、Fy=0和F2=-ρg;g為重力。
1.1.3 結構動力學控制方程
采用有限元法解算結構運動方程對運動方程進行有限元離散,如公式(6)所示。

1.2 湍流方程
ANSYS為使用者提供了多種湍流方程,對于結構近壁處以及尾流的模擬大多采用SST k-ω。SST k-ω 模型與k-ε 模型相比,它更加接近實際工況,對管道內渦激振動的振幅、振頻響應以及相關特性參數的模擬更準確,因此選用SST k-ω 的湍流模型。
SST k-ω 模型的計算公式如公式(7)所示。

式中:φ1為改進的內部邊界層k-ω 模型;φ2為標準的k-ω模型;F1為混合函數。
1.3 幾何模型及網格劃分
立管的外部流域為1個六面體,流場長40D、寬20D,L/D=5。直徑為18 mm、長 為3.6×103mm的細長圓柱,壁厚為2.5 mm,底端固定在流場底部,圓柱體頂面為自由端[4]。流場的入口流速為0.1 m/s,流體介質為水,密度為1 025 kg/m3,雷諾數為1 845。
采用ANSYS對幾何模型進行雙向流固耦合模擬,考慮到計算量、分析網格質量以及模擬形變區域,該文決定采用擴散光順法的動網格技術。由于雷諾數較高且立管周圍的流動情況比較復雜,因此需要對圓柱進行“O”型分塊,對圓柱壁面網格進行加密,如圖1所示。
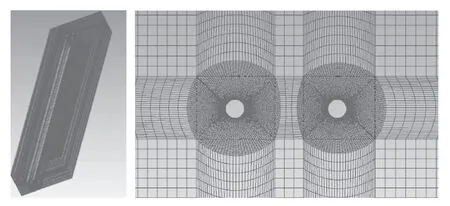
圖1 串聯立管外流場(左)及邊界層網格(右)
2 模擬結果及討論
2.1 流場數值模擬方法驗證
在應用ANSYS進行流固耦合模擬之前,需要對無耦合情況進行數值模擬[5],并將模擬獲得的立管橫向位移時間歷程和運動軌跡圖與實驗結果進行對比。通過分析對比結果可以確定所采用的網格劃分方式、時間步長、湍流模型和數值模擬方法是能夠準確對立管內渦激振動現象進行數值模擬的。立管自由端橫向振幅如圖2所示,可以看出實驗結構的橫向位移較大,約為±0.73D,數值模擬得出橫向振幅約為±0.71D。數值模擬得出的斯特勞哈數約為0.191,與B.sannati實驗結果吻合較好。
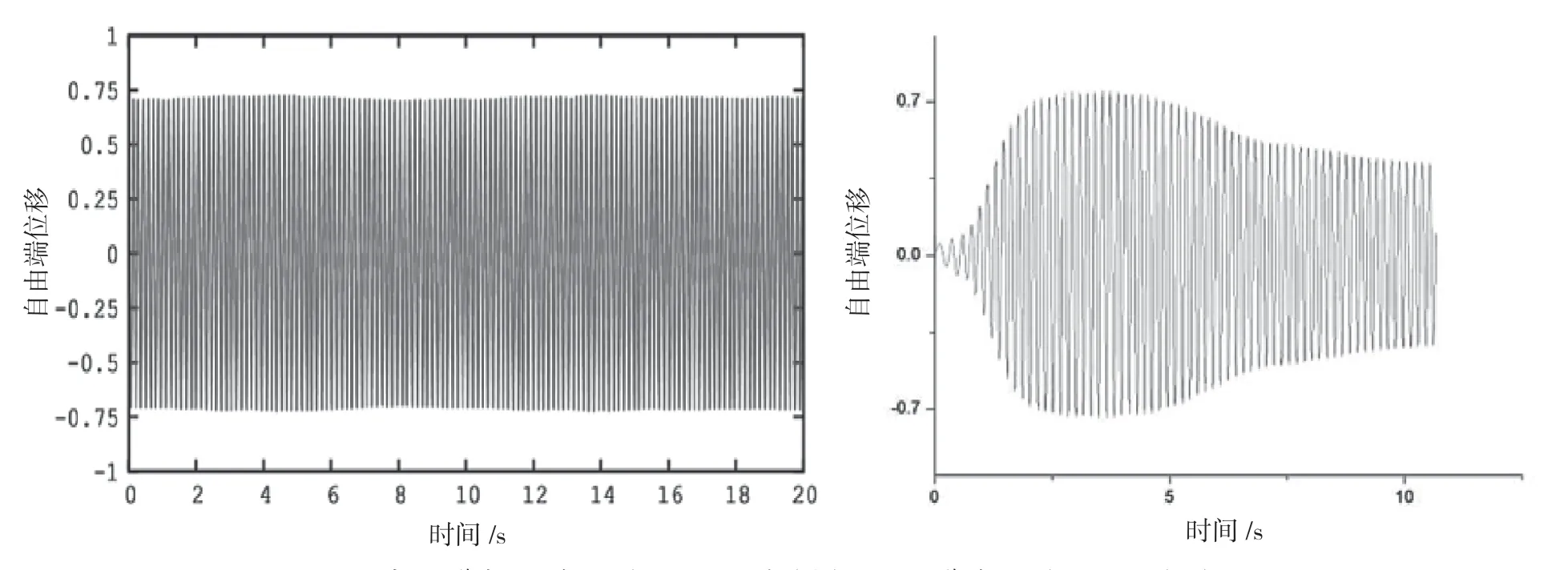
圖2 實驗立管自由端橫向位移時間歷程曲線(左)和FSI立管橫向位移時間歷程(右)
2.2 不同頂部約束條件下立管振動參數分析
圖3和圖4為不同頂部約束條件下立管升、阻力系數幅值的變化曲線。當對管道施加的頂部約束增加時,管道的上下游升力系數也明顯增大,下游管道提升的幅度要更明顯一些。主要是因為上游立管釋放的渦流附著在下游立管上,下游管道受到上下游渦流的共同作用,會出現頂部張力增加、結構的固有頻率增大、結構的響應幅度減小、能量耗散減少以及結構上下游壓差增加的情況,從而導下游立管的升力系數的最大幅值約為上游立管的1.5倍。對于阻力系數,上游管道的尾流并沒有增加管道內流體對結構的作用力,由于上游立管尾流的速度要小于正常流速,因此下游管道受到上游管道和自身脫落的旋渦的共同作用,會使下游立管順流向的壓力差不斷地變化,從而導致下游立管的阻力系數小于上游阻力系數且幅值相差較大。
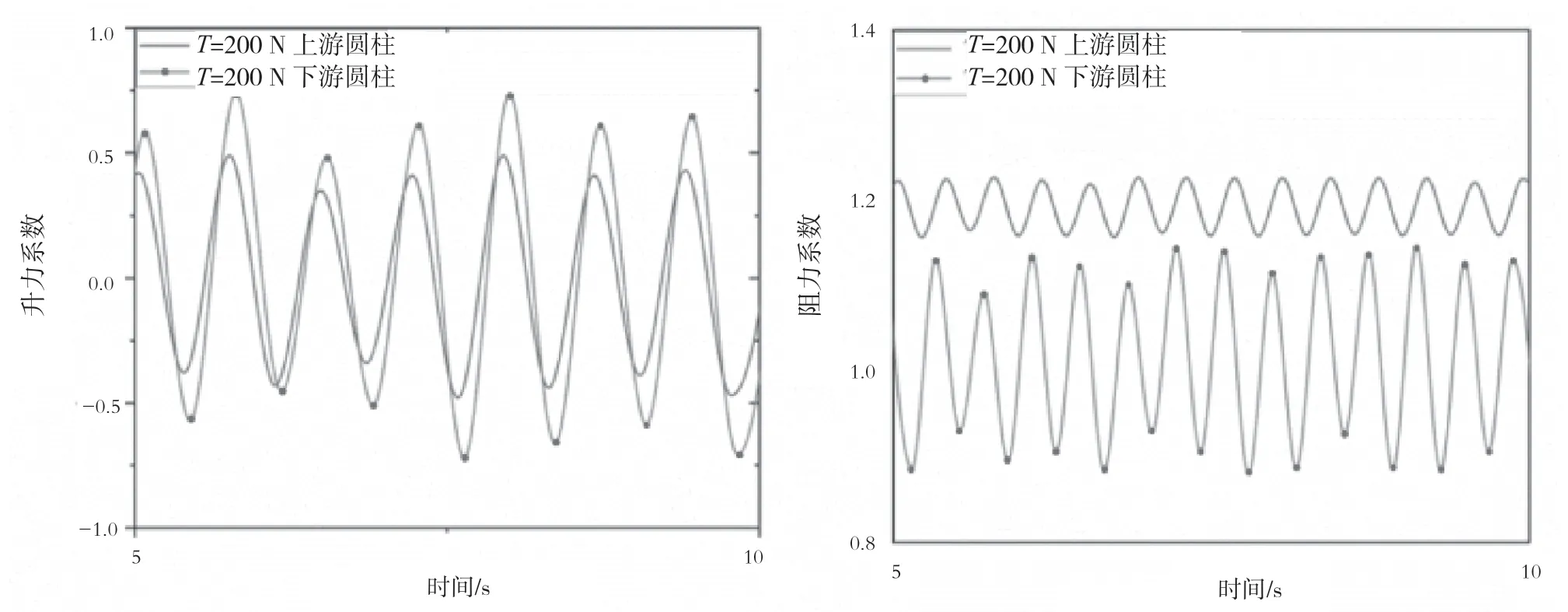
圖3 T=200 N時串聯立管升力系數(左)與阻力系數(右)
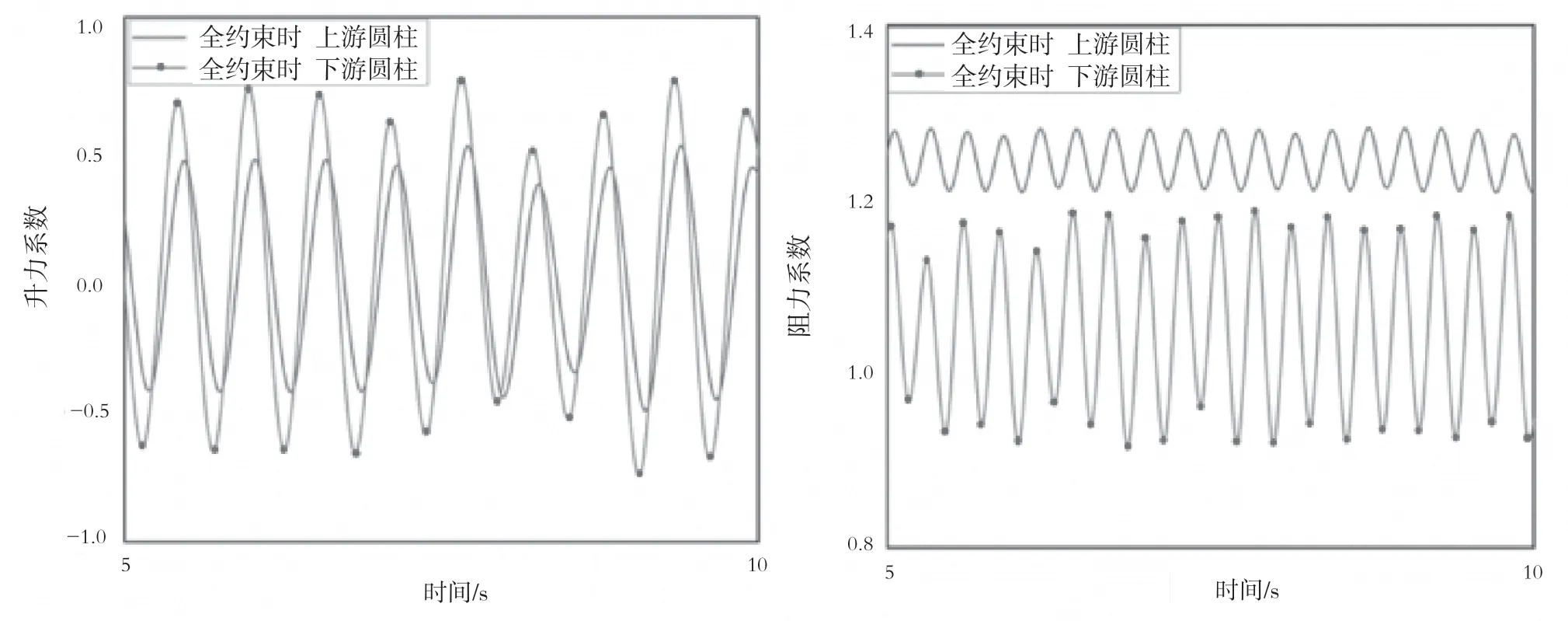
圖4 頂部全約束時串聯立管升力系數(左)與阻力系數(右)
通過模擬得到的升、阻力系數幅值隨時間變化的曲線表現出周期性的特點,立管上下游的升、阻力系數的變化頻率基本不隨頂部約束的變化而變化,升力系數變化頻率約為阻力系數變化頻率的1/2,下游立管的頻率幅值要遠小于上游立管的頻率幅值。
2.3 不同頂部約束條件下立管振幅與振頻分析
在模擬的過程中,橫坐標為沿著管道軸向提取的5個不同高度,關注點位置相對于管長比例分別為Z/L=0.1、Z/L=0.3、Z/L=0.5、Z/L=0.7以及Z/L=0.9,縱坐標為均方根與立管直徑之比(Xrms/D、Yrms/D)。不同頂部約束條件下上下游立管的順流向與橫流向沿立管軸向高度的均方根振幅曲線如圖5、圖6所示。管道振動均方根振幅曲線呈對稱的拋物線狀,管道上下游都呈現出先增加后減小的趨勢,在拋物線對稱中心(Z/L=0.5)產生最大的均方根振幅,越靠近兩端,振幅響應幅度越小。隨著頂端載荷的不斷增大,均方根振幅曲線逐漸趨近于直線,振動偏離初始位置且振幅程度減弱。在順流向上,管道上游對下游產生“屏蔽”效應,下游立管的均方根幅值遠小于上游立管;橫流向下游立管受到上游立管和自身釋放的渦流的共同作用,均方根振幅大于上游立管。
不同頂部約束條件下上下游立管的振動響應頻率會改變管道的頂端約束,管道結構主要呈現出多頻振動的現象,同流向上下游管不同位置的振頻相同。隨著立管頂端載荷的不斷增加,順向流立管的振動響應頻率也不斷增大,橫向流立管的振動響應頻率不變。因此,雖然增加頂端約束可以減小立管振動幅度,但是也會增大立管的響應頻率,當響應頻率接近于結構的固有頻率時,結構發生共振的風險增高,這樣會降低設備的使用壽命,嚴重的可能會造成管體損壞。
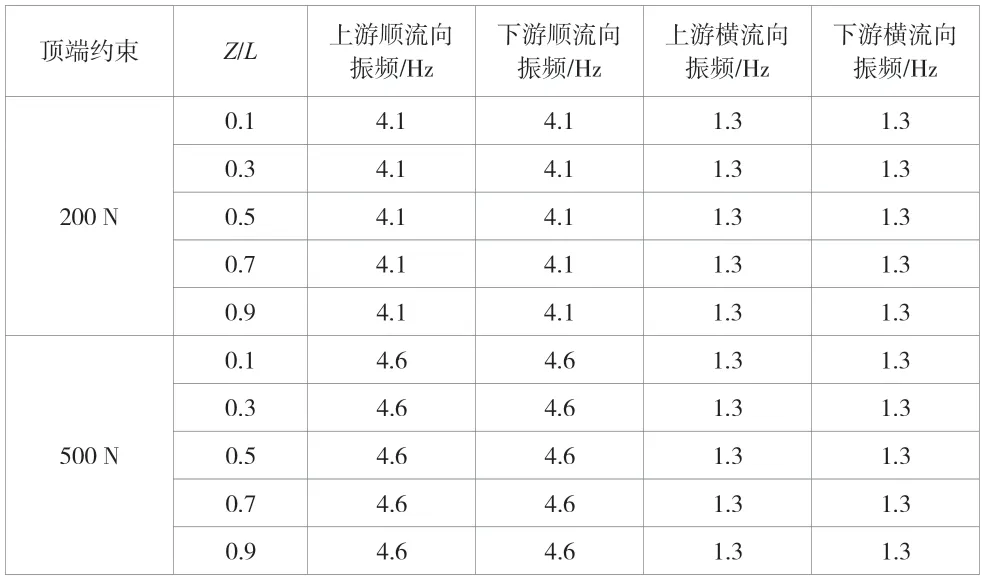
表1 不同頂端約束下串聯立管振頻
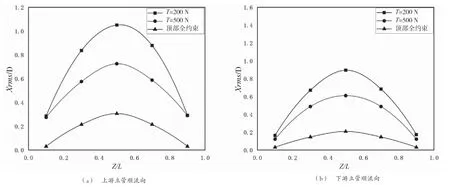
圖5 不同頂部約束條件立管順流向均方根振幅
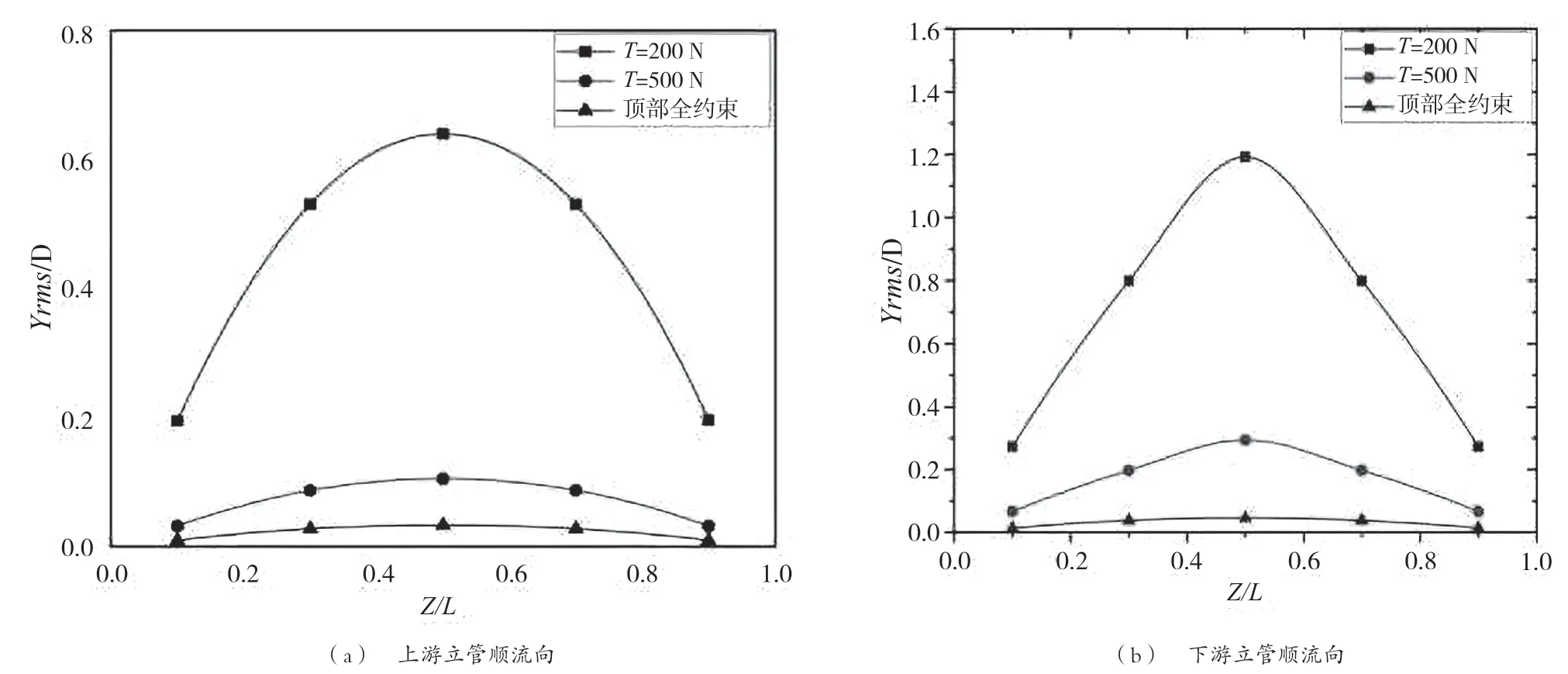
圖6 不同頂部約束條件立管橫流向均方根振幅
3 結論
該文對不同頂部張力的串聯立管渦激振動時尾流的干涉效應進行模擬,得到的主要結論如下:1)應用ANSYS對無耦合情況下的圓柱擾流流場進行數值模擬,模擬獲得的立管橫向位移時間歷程和運動軌跡圖與B.sannati實驗結果吻合較好,模擬得出的斯特勞哈數約為0.191,可以證明數值模擬結果的準確性。2)隨著立管頂端約束的不斷增大,立管上下游升、阻力系數呈現增加的趨勢。下游管道受到來自上游管道和自身釋放的渦流的共同作用,升力系數最大幅值遠大于上游管道(約為上游管道的1.5倍);對于阻力系數來說,上游管道的尾流速度小于正常流速,并且受到上游立管與自身脫落的渦流的共同作用,下游立管阻力系數小于上游阻力系數,阻力系數變化頻率大約是升力系數變化頻率的2倍。3)隨著頂端載荷的不斷增大,均方根振幅曲線逐漸趨近于直線,振動偏離初始位置且振幅程度減弱。在順流向(X方向),管道下游受到來自管道上游的“屏蔽”效應,下游立管的均方根幅值遠小于上游立管;在橫流向(Y方向),下游立管受到上游立管和自身釋放的渦流的共同作用,導致下游立管的均方根振幅大于上游立管。4)對比不同約束條件下的振動頻率圖,立管結構主要呈現出多頻振動的情況,不同位置的振動頻率相同,順流向的振動頻率要大于橫流向的振動頻率。隨著立管頂端載荷的不斷增加,立管的振動響應頻率也不斷增大。因此,雖然增加頂端約束可以減小立管的振動幅度,但是也會增大立管的響應頻率,當響應頻率接近結構的固有頻率時,結構發生共振的風險增高,這樣會降低設備的使用壽命,嚴重的可能會造成管體損壞,因此選擇合適的頂部張力也是值得研究的問題。

