級聯H橋SVG控制策略研究

張 飛 王 瑞

（內蒙古科技大學，內蒙古 包頭 014010）

0 引言

針對智能配電網，如果要提高功率系數，就需要采用無功補償設備減少變壓器以及線路的損耗，從而改善配電環境。因此，有效選取無功補償設備對電網來說是非常關鍵的。好的設備可以減少傳輸損耗、提高電能質量[1]。否則，就可能導致電壓波動、諧波增大等。對于無功補償裝置的選取，以TCR為代表的靜止無功補償器（SVC）與靜止無功發生器（SVG）進行比較，SVG以快速性、多重化拓撲、補償電流諧波含量小的優勢[2]。然而，分布式電源的引入打破了電網的平衡。因此，級聯H橋SVG憑借自身模塊化、擴展性強以及具備良好的諧波特性而被普遍使用。因此該文研究并分析了SVG的檢測、控制方法。

1 基于瞬時對稱分量法ip-iq 的無功檢測方法

電網不平衡時，采用基于瞬時對稱分量法的ip-iq法來檢測無功。瞬時對稱分量法在該處的作用為分離電網側電壓及電流，并得到它們的正負序分量。首先，利用Clark變換對三相電壓、電流進行轉換，如公式（1）所示。

這就是幅頻響應，φ為函數u（t）在時間為t處的相位、U+、U-分別為電網電壓正負序分量的有效值。可以得到新公式，如公式（3）所示。

將公式（2）與公式（3）聯立，得到新公式，如公式（4）所示。

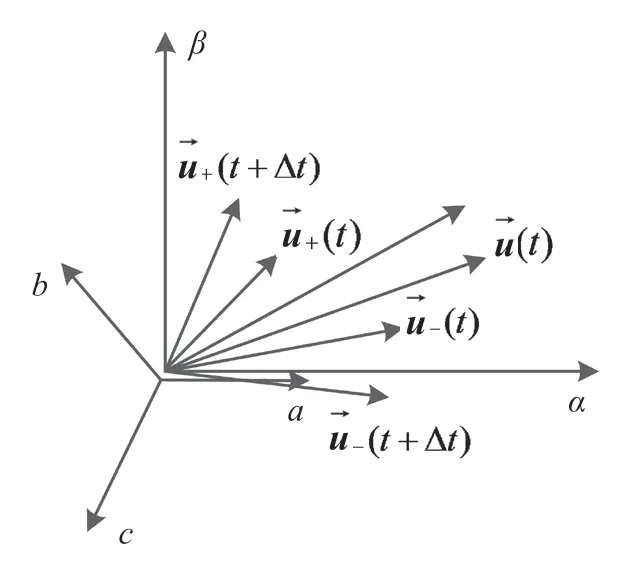
圖1 平面上的三相電壓向量圖

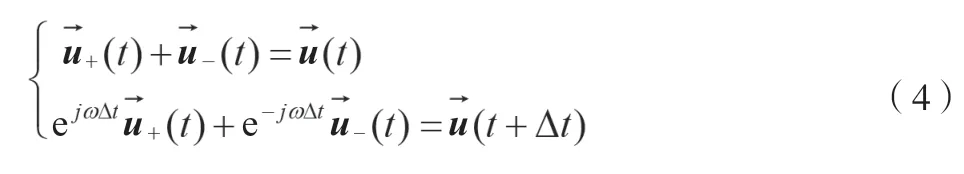
當時間為t時，要得出電壓的基波正、負序分量，應對上式求解，如公式（5）所示。

式中：ua1、ub1和uc1為三相電壓正序分量；ua2、ub2和uc2為三相電壓正序分量。

通過公式（1）、公式（6）、公式（7）以及公式（8）可以得到新公式，如公式（9）、公式（10）所示。

綜上所述，可以得出正負序分量、瞬時值之間的關系，并由此得到基波的正負序電壓、電流。同時，SVG系統三相平衡，可以直接利用ip-iq法獲取系統的參考電流，原理如圖2所示，它是對有功和無功電流進行解耦，利用鎖相環的信號發生電路，從而得到與網側電壓相位相同的正余弦信號。圖中，ua、ub、uc與ia、ib、ic分別為三相電網的電壓和電流；ua1、ub1、uc1與ia1、ib1、ic1分別為三相電壓正序分量和正序分量；iα+、iβ+為αβ坐標系中的正序電流分量；ip+、iq+為pq軸上的正序電流分量；ip+為p軸上的正序電流基波分量；iαf+、iβf+為αβ坐標系中的正序電流基波分量；iaf+、ibf+和icf+為三相電流正序基波分量；iaref、ibref和icref為三相電流諧波分量；PLL為鎖相環；C32指將abc坐標系中的電流分量轉換到坐標系中；C指將αβ坐標系中的電流分量轉換到pq軸上；LPF為低通濾波器，用來濾除諧波分量；C-1為C的逆變換；C23為C32的逆變換。

圖2 補償電流計算方法原理圖

2 H橋級聯SVG控制策略

SVG之所以能夠穩定、連續以及快速補償電網無功，是因為H橋單元直流側的電容穩定、平衡。但是由于它結構復雜且呈模塊化，因此有必要采用分層控制，將其分為直流側電壓整體均衡控制、各相之間電壓均衡控制以及每相各模塊電壓均衡控制[3]。三層控制體系之間相互作用、相互協調，與電流內環控制配合，使H橋級聯SVG能夠快速、穩定地輸出電流。

2.1 直流側電壓整體均衡控制

SVG在不平衡條件下的整體控制策略如圖3所示，電壓環為電流環提供正序有功參考，正、負序電流環都采用比例微分控制（PI控制），從而達到完整補償正負序有功電流、負序無功電流的目的。不平衡條件下對SVG進行控制的核心是快速、精確地分離正負序電流分量，同時均衡、穩定各相間的電壓。

圖3 H橋級聯SVG系統的電流和直流側總電壓控制模型

2.1.1 電流內環參數設計

SVG在dq坐標系的數學模型如圖4所示，由圖4可知dq軸之間能夠耦合。

由圖4可以得到公式，如公式（11）所示。

那么圖4可以簡化為如圖5所示的模型。

對Ud（s）、Uq（s）引入PI控制，kp、ki為PI控制的系數，如公式（12）所示。

將公式（11）和公式（12）聯立，可以得到新公式，如公式（13）所示。

由公式（13）可以得到SVG的解耦控制的數學模型，如圖6所示。根據圖6可以得到電流內環控制框圖，如圖7所示。在dq軸，因為圖7中的控制參數是一致的，所以以d軸為例，設比例控制系數kPWM=1，那么電流內環傳遞函數如公式（14）所示。

公式（14）所示系統為二階帶零點系統。根據實際工程，外環的響應時長大于等于一個周期（0.02 s），內環響應時長為一周期的0.1倍或者小于0.1倍。采用PID調諧器模塊將響應時間設置為0.002 s、暫態系數為0.86，就可以得出整定后的系數kp=31.54、ki=3217.9。

2.1.2 電壓外環參數設計

在理想狀態下，建立dq坐標系下H橋級聯SVG的數學模型有利于分別控制SVG的有功、無功分量。此時，將d軸對應有功分量，q軸對應無功分量，將給定的SVG三相平均電壓作為d軸的參考值，將負載側無功電流的逆相作為q軸上的參考值，d軸上的有功分量控制框圖如圖8所示。系統的有功功率傳輸滿足公式（15）。

圖4 dq 坐標系下SVG的數學模型

圖5 dq 坐標系下SVG系統的簡化解耦數學模型

式中：usd（t）、usq（t）為電網電壓在dq軸的分量；icd（t）、icq（t）為SVG輸出電流在dq軸的分量；N為SVG的鏈路數；Cdc為SVG直流側電容值；udc為SVG直流側電容電壓。

當系統穩定運行時，usd（t）=Us，usq（t）=0。其中，Us為電壓在d軸上的分量。經過拉式變換，可得公式如公式（16）所示。

式中：G（s）為SVG輸出電流的開環傳遞函數；Udc（s）為SVG直流側電壓瞬時值；Udcref為直流側平均電壓的有效值；s為復數。

公式（16）的系統為四階系統，釆用PID調諧器模塊整定參數。將電壓外環的響應時間設置為0.02 s，暫態系數設置為0.79。通過整定，系數kpv=3.4，kiv=0.591（考慮其正負序分量）。其交流量關系式如公式（17）、公式（18）所示。

分別對公式（17）和公式（18）進行dq變換和dq反變換，如公式（29）所示。

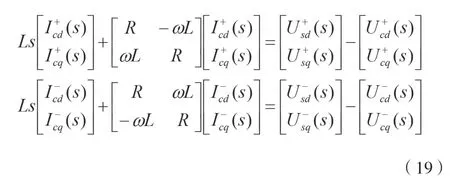
式中：+、-號分別為正序分量、負序分量；s為復數。

由公式（19）可知，在不平衡條件下，通過分別對dq軸上電壓、電流的正負序分量進行解耦來控制電壓與電流的方法是可行的。

2.2 各相之間電壓平衡控制

對于不平衡條件，附加零序電壓的相間控制策略是系統使用最廣泛的策略之一[4]。

假設當前電網不平衡是由電網電壓不對稱、負載不平衡以及三相損耗差異共同導致的，那么就采用附加零序電壓的控制策略來確保相間均衡。最終控制目標也就是使波動量等于0，如公式（20）所示。

式中：ΔPa、ΔPb和ΔPc為實際有功相對于三相平均有功的波動量，則如公式（21）所示。

式中：Up、Un為相電壓正、負序分量的有效值；Ip、In為正、負序電流有效值；αn為負序相電壓分量初始相角；βp為SVG正序輸出電流分量的初始相角；βn為SVG負序輸出電流分量的初始相角；Uo、φo為所疊加的零序電壓有效值（V）、初始相角。

圖6 dq 坐標系SVG的解耦控制數學模型

求解公式（21）就可以得到零序電壓的幅值、相角表達式，如公式（22）、公式（23）所示。

式中：ΔPoa、ΔPob零序電壓引起的a、b兩相功率的波動量。

ΔPoa、ΔPob的值，如公式（24）、公式（25）所示。

把公式（22）、公式（23）～公式（25）結合起來，就可以得到附加零序電壓的均衡控制策略原理圖，如圖9所示。

通過比較得到ab相與c相平均電壓的差，對其進行PI控制。然后通過正負序分離模塊獲取正負序電壓、電流的幅值和相角。由公式（24）和公式（25）可以求得零序調壓功率的波動量，由公式（23）和公式（24）可以得出需要的零序電壓值。

2.3 每相各模塊電壓平衡控制

利用基于有源矢量疊加的方法，控制框圖如圖10所示。將電流的方向與電壓差相乘的方法不但可以確保上層控制不受疊加的影響，而且還規避了電流幅值引起的不穩定要素。由于電流超前電壓方向90°，因此cos（ωt）、cos（ωt-2π/3）以及cos（ωt+2π/3）能夠等同于ica、icb和icc的方向。

實質上，比例系數P的值越大，控制響應速度就越快，控制效果也越好[4]。然而，當P值過大時，任何電壓差都可能導致調制波的分量疊加過大，從而導致控制策略不能起到控制作用。因此，有必要計算P的值。因為SVG由多個H橋模塊構成且上層控制利用的是雙閉環，很難建立一個數學模型來顯示對直流母線電壓的控制。所以從能量傳輸方面出發，該文設計了比例系數P的參數。如圖9所示，矢量必須在功率的調控范圍內疊加，如公式（26）所示。

式中：Δufk為第k個單元模塊的調制波波動量；upmax、unmax為某個單元模塊電容的電壓值小于、大于平均電壓時所需要注入的最大電壓矢量。

則各量之間的關系，如公式（27）～公式（29）所示。

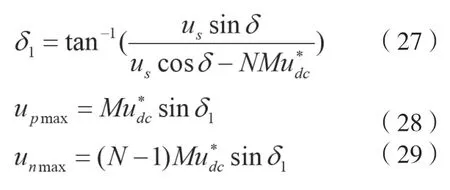
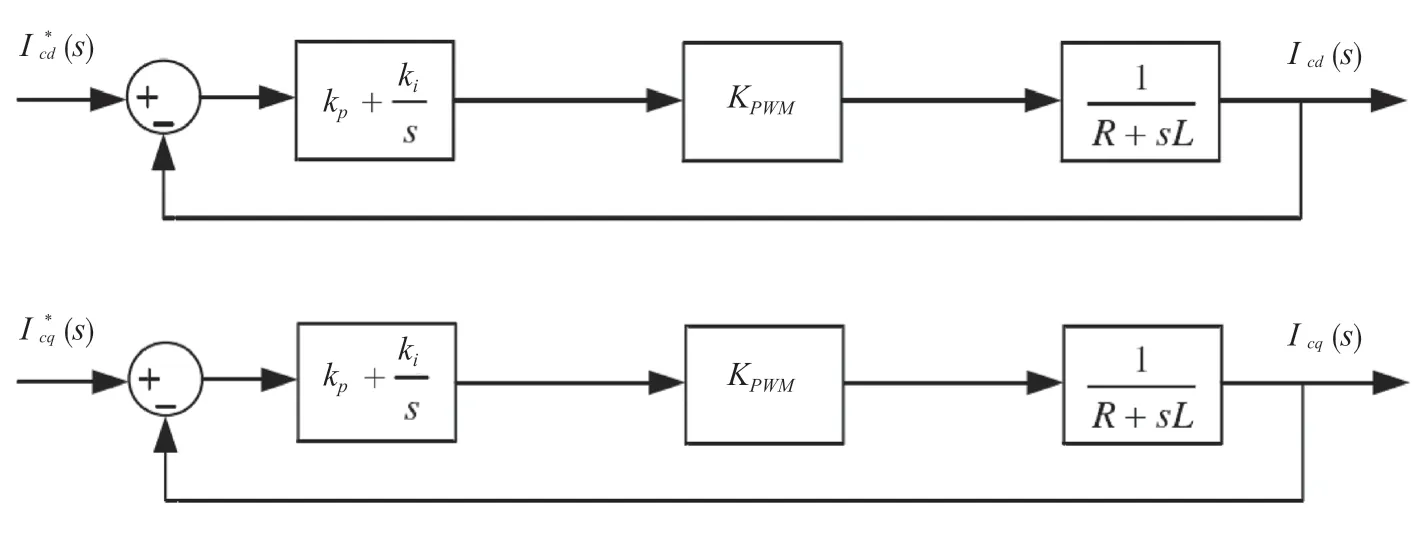
圖7 dq 坐標系的SVG的解耦控制框圖

圖8 H橋級聯SVG系統的d 軸有功分量的控制框圖

根據圖10可以得到公式，如公式（30）所示。

式中：Δuck為第k個單元電壓與本相平均電壓差。。

由公式（26）～公式（30）可以得到新公式，如公式（31）、公式（32）所示。

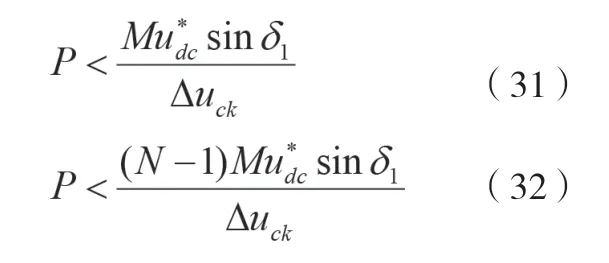
Δuck工程設定值一般為0.05～0.1，在公式（31）和公式（32）中代入系統的有關參數，就可以得到P的參考范圍。有功矢量的疊加實際上是在調節各模塊的有功功率損耗，因此各模塊電壓電流的乘積不應該小于實際的有功損耗[4]。假定某個模塊的有功損耗為Pk，那么就有表達式，如公式（33）所示。

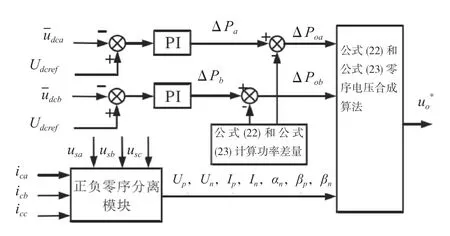
圖9 基于附加零序電壓的相間均衡策略

圖10 改進的直流母線電壓均衡策略控制框圖

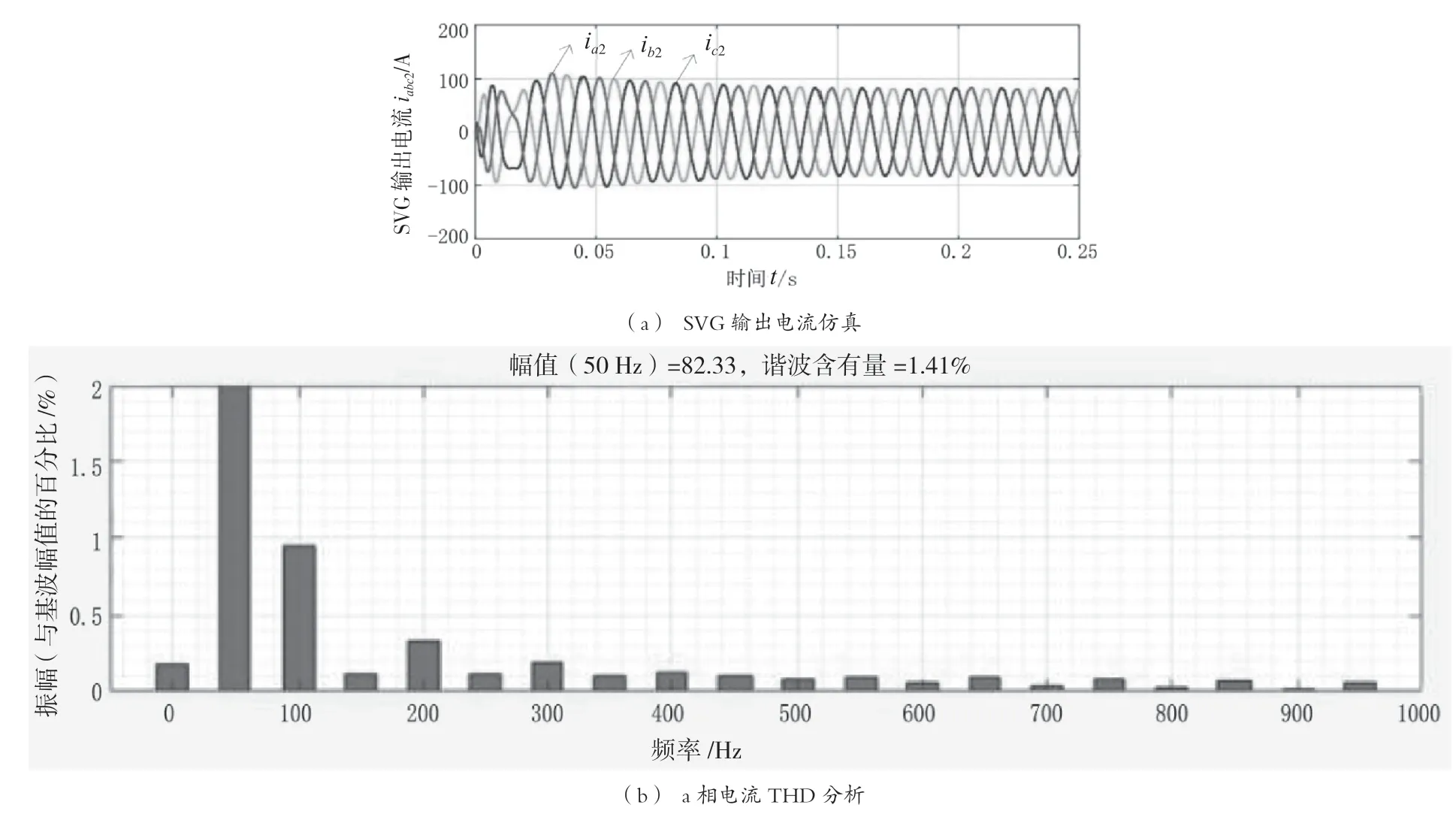
圖11 H橋級聯型SVG輸岀電流效果圖（額定負載）

式中：Ic為SVG輸出的額定電流有效值。

根據工程經驗，在10 kV、1 000 kvarSVG系統中，通常Pk≤40 W，則P的范圍是0.139＜P＜0.479。

3 仿真分析

針對10 kV、1 000 kvar的SVG系統，為了分析使用的檢測、控制方法是否有效，在Matlab平臺上進行仿真。其系統參數如下：H橋模塊直流測電壓800 V，單相級聯H橋個數N=12；電網頻率f=50 Hz，載波頻率fc≤500 Hz。結合實際及計算，得到連接電感L=31.83 mH，等效損耗電阻R=1.02 Ω，直流側電容C=517 μF；設置負載側電感L=159 mH，電阻R=50 Ω。

仿真系統采用單級倍頻CPS-CPWM（載波移相式正弦脈寬調制技術）調制SVG系統輸出電壓的波形質量、系統損耗率以及效率[5]。

3.1 電網平衡

圖11顯示了SVG輸出電流的波形及THD值。圖11（a）為SVG側輸出電流的仿真，從圖中可以看出，三相輸出電流在0.15 s后達到穩定狀態，這也證明所設計的SVG充分補償了無功，體現了參數設計是有效的。圖11（b）顯示了單相電流的THD 值。由圖可知，THD=1.41%，符合國家并網標準。

圖12 不平衡條件下電壓、電流仿真波形圖

圖13 不平衡條件下SVG補償的電流仿真波形圖

3.2 電網不平衡

圖12顯示了電壓、電流的波形，圖中縱坐標為輸出電壓usa、usb、usc縮小200倍后的電壓值。usa、usb、usc是電網側三相電壓，isa、isb、isc為電網側三相電流。經過0.15 s，公共連接點處的電壓、電流相位一致，此時SVG充分補償了無功。由于負載不均衡，電流分離模塊的正負序電流增加了部分延遲時長[6]，因此仿真模型穩定補償的時間比平衡狀態更長。

對于電網不平衡，SVG的輸出電流波形如圖13所示。圖13（a）中，iabc2為SVG的輸出電流。由于iabc三相對稱，因此SVG輸出的負序分量對負載產生的負序分量進行了完全補償。由圖13（b）可知，SVG輸出電流THD值符合標準，連接電感可以很好地抑制諧波。

4 結論

級聯H橋SVG是智能配電網中常用的無功補償設備，該文對級聯H橋SVG的檢測、控制方法進行了闡述和研究，采用了基于瞬時對稱分量法的ip-iq檢測法能夠檢測電網電流的有功分量、無功分量；直流側電壓的三層控制體系能夠相應地穩定每一層的直流測電壓。該文還利用仿真的形式對平衡和不平衡條件下的電網SVG系統進行分析，仿真時所用的CPS-SPWM能夠跟蹤補償無功和負序電流。結果檢驗了SVG能夠有效地提高系統運行的功率因數并使電網達到平衡，同時也為實際工程的設計提供了依據。