HPM視角下深度學習課例開發
——以點到直線距離公式再證明為例
甘肅天水市一中 (741000) 文貴雙
淺層學習以知識獲取和記憶訓練為主要特征,學習處于相對較低的認知水平;深度學習則以知識深度加工、意義建構和深度思維為主要特征,以理解、應用、分析、推理、綜合、評價、創造等高層次認知活動為主要學習活動,學習處于高認知水平.深度學習是一種主動的、探究式的、有意義的學習過程,是深入內容本質的概念理解、知識探究、問題解決等相對復雜的學習過程,學生能夠將學到的知識遷移與應用,實現知識的深層加工、深刻理解以及長久保持,并實現“高層次認知能力”和“高階思維”的發展,促進深刻理解的同時幫助他們把握學習內容的核心與聯系.
怎樣讓學生進入深度學習的狀態?郭華教授認為,在教師引領下,教學中圍繞具有挑戰性的主題,引導學生圍繞學習內容深入思考、積極對話,表達與展示自己的思維過程,形成深層次的認知參與和積極的情感體驗.而挑戰性的主題哪里來?HPM案例就是深度學習的好素材.
HPM(數學史與數學教育)中的歷史發生法就是通過數學史料的研究,發現數學對象和數學思維的發生發展規律,為解決數學教學的現實問題提供歷史的借鑒和支持.因為任何數學知識都是人類數學認識不斷建構的結果,從簡單到復雜,從直觀到抽象,從經驗概括到形式構造,經歷漫長的歷史過程,這是數學家或幾代數學家獨特而深邃的高級思維方式的成果.他們的高級思維過程是學生進行思維活動的典范,他們的思維通過教師的加工處理來示范引導學生的深度學習.本人在高三復習交流會上上了一節“點到直線距離公式的再證明”的觀摩課,示范借力HPM來引領學生深度學習,引起大家的熱評.
1 課堂實錄
師:我們在高一學習了點到直線的距離公式,由于當時受到所學知識的限制,該定理的證明方法單一,現在我們已經學完了高中數學全部內容,掌握了許多工具,今天我們再證“點到直線的距離公式”,公式如下:
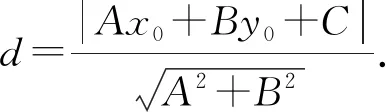
1.1 再現教材公式的推導過程
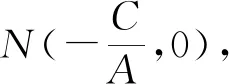
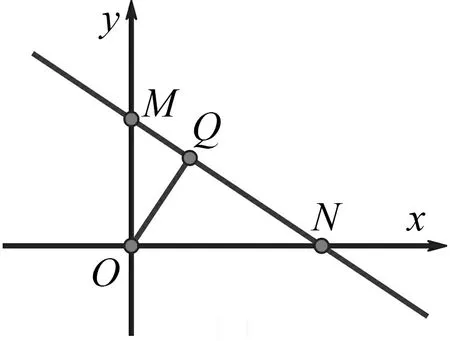
圖1
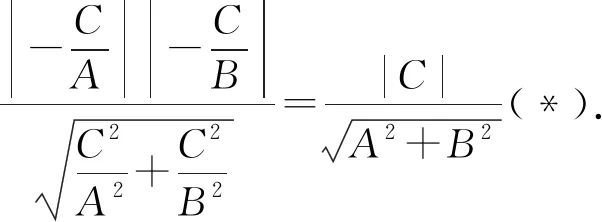
哪位同學得到啟發?
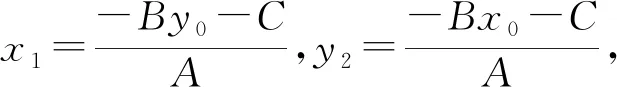
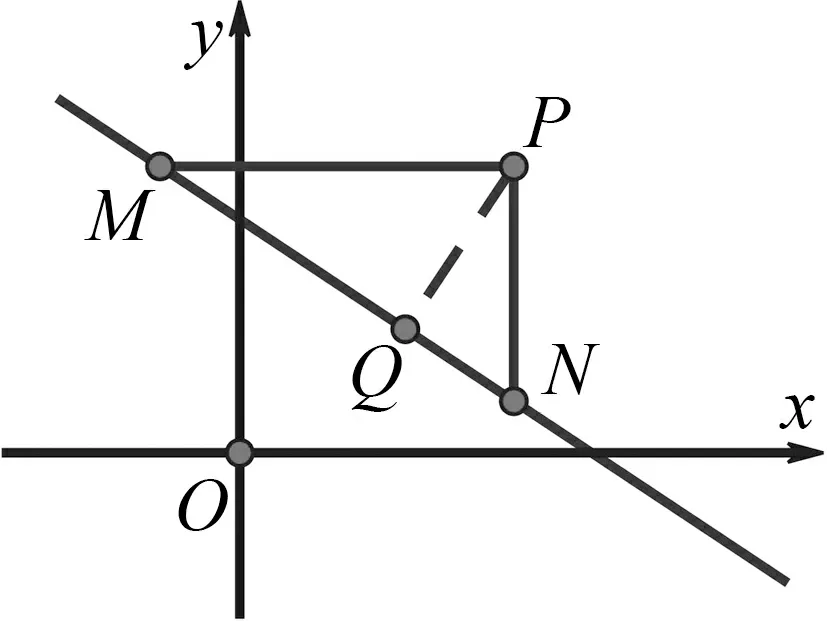
圖2
師:19世紀末,英國數學家約翰斯頓(W.J.ohnston),將點線距離轉化成三角形的高,其證明和上面證法一樣.下面我們從不同的視角探討其他證法.
1.2 多視角尋找證法,培養學生思維的發散性
圖3
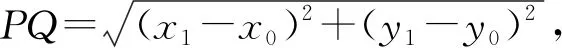
生:我有一個不需求Q的坐標的證法.
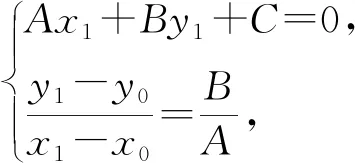
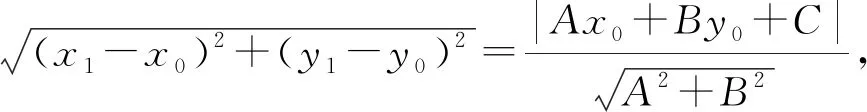
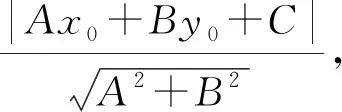
師:不錯,回到點線距離的定義,配湊出目標.19世紀的英國數學家楊格(J.R.Young)是從方程組中解出(x1-x0),(y1-y0),代入距離公式得到公式.到了20世紀,有人在楊格的基礎上采用設而不求的方法,將方程組兩邊平方,從而簡化了運算,和本解法一樣.
生:類比斜面上物體受力分析圖,本題作如圖4的圖形,直角△PQM中,∠QPM等于直線的傾斜角或其補角.
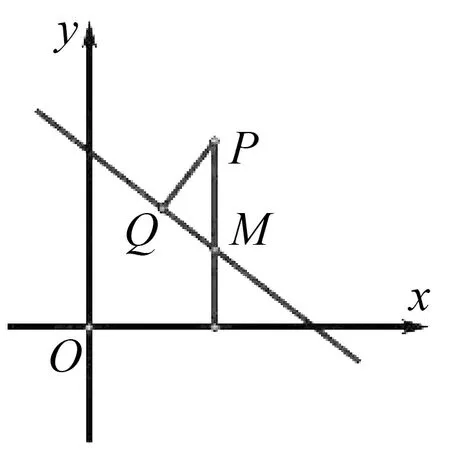
圖4

師:這個證明與19世紀英國著名數學家托德亨特(I.Todhunter)證法一樣,真是英雄所見略同.
生:受到空間向量求點到面距離的啟發,可以用向量證明.
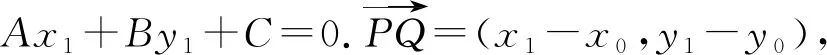
師:20世紀40年代,向量知識逐漸出現在西方教科書中,教科書的編者給出了這樣的證法.
生:由于點P到直線l的距離是點P到直線l上任意一點距離的最小值,故可以得出目標函數,利用二次函數的最值求得點P到直線l的距離公式,但推導比較復雜.
師:想法自然,但運算復雜.把展示的機會留給老師啊,老師提供如下證法:
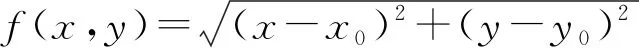
20世紀,美國數學家泰勒(A.E.Taylor)在其《微積分與解析幾何》著作中提供上述證法.抓住距離概念的本質,巧用柯西不等式是難點.
星移物換,穿過浩渺的時空,發現古代數學家們的證法與我們的相同,為同學們的聰明才智點贊.
2 結語
《普通高中數學課程標準》指出,定理教學的意義不僅在于學生掌握“書本知識”,更重要的是讓他們從中體驗數學家概括數學定理的心路歷程,通過典型問題的設置和學生的探索,使學生理解定理逐步形成的過程,體會蘊含在其中的思想,追尋數學發展的歷史足跡.然而實際教學中,教師通常為了擠出時間多做練習,“輕松”地給出定理,學生失去了“自主探索定理產生的背景及蘊含的思想,親身經歷定理的發生、發展的過程”,失去了“深刻體驗、直觀感知、觀察發現、抽象概括、歸納類比、反思與建構等思維歷程”,失去了提升學生核心素養的大好時機.加之,學生學習受內容的制約,后續學習的方法用不到定理的證明中,這就需要我們在恰當的時間點,把定理放在更大的系統中,根據學生學習的不斷深入,對定理(公式)二度認識,從不同的角度推導證明.本節課所有的證法只要教師啟發得當,學生全身心投入探究,大家合作交流都能發現,教師不失時機說明這是歷史上那位數學家的證法,并對學生贊揚,使學生產生成果的喜悅,增強學習的興趣.這正是華東師大汪曉勤教授提出的,數學史融入數學教學六種教育價值:知識之諧、方法之美、探究之樂、能力之助、德育之效、文化之魅.
美國著名數學家和數學史學家M·克萊因認為,歷史上數學家遇到的困難和挫折,課堂上同樣學生也會遇到,因而歷史對于課堂教學具有借鑒和指導作用.教材往往按照數學知識的邏輯體系進行編寫,而這種邏輯體系下的知識呈現與知識的歷史真實發生過程往往不一樣,在這樣的過程中學生很難體會到數學家的思維歷程,學生的思維完全被老師的講解所代替,學生的認知是低水平,思維得不到最大的優化,因此,在教學中我們可以適當借用HPM案例展示數學家如何思考問題,在遇到困難時如何選用合適的思維方式解決問題,讓學生感受到數學家的卓越智慧,學習他們研究數學問題的思維方式方法.

