“磁發散,磁聚焦”規律及其應用
河北省內丘中學 袁振卓054200

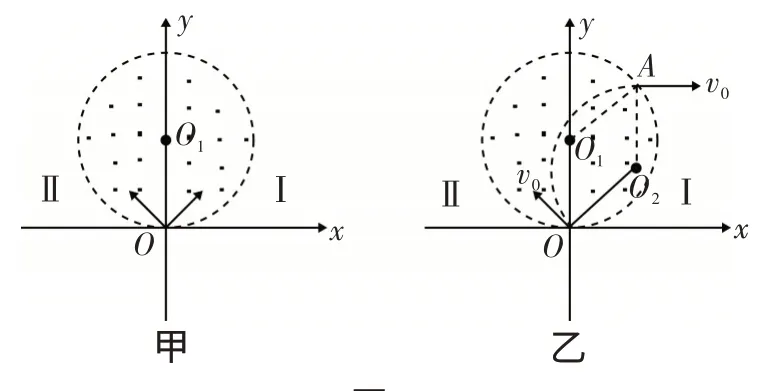
圖1

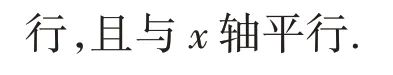
結論1:帶電粒子從圓形有界磁場邊界上的某點射入磁場,如果軌跡圓半徑和磁場圓半徑相等,則粒子出射方向都平行,且與過入射點處的切線方向平行.
同理我們還可以得出:
結論2:平行射入圓形有界磁場的相同帶電粒子,如果軌跡圓半徑與磁場圓半徑相等,則這些粒子都從磁場邊界上的同一點射出磁場.
從以上兩個結論可以得出,當軌跡圓半徑與磁場圓半徑相等時,圓形勻強磁場具有與光學元件凸透鏡類似的“發散”和“聚焦”作用.所以我們把上述兩個結論分別稱之為“磁發散”和“磁聚焦”結論.下面通過實例分析兩個結論在具體問題中的應用.
例1如圖2甲所示,ABCD是邊長為a的正方形.質量為m、電荷量為e的電子以大小為v0的初速度沿紙面垂直于BC邊射入正方形區域.在正方形內適當區域中有勻強磁場.電子從BC邊上的任意點入射,都只能從A點射出磁場.不計重力,求:(1)此勻強磁場區域中磁感應強度的方向和大小;(2)此勻強磁場區域的最小面積.
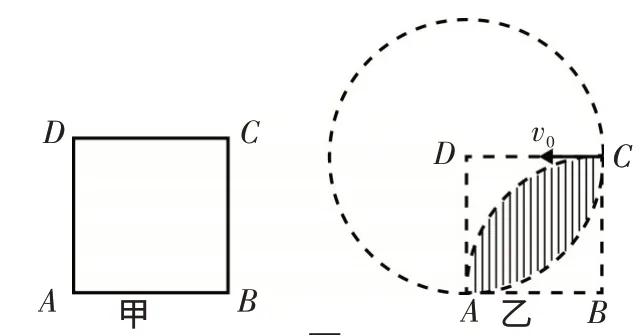
圖2

例2電子質量為m,電荷量為e,從坐標原點O處沿xoy平面射入第一象限,射入時的速度方向不同,速度大小均為v0,如圖3所示.現在某一區域內加一方向垂直紙面向外的勻強磁場,磁感應強度為B,若這些電子穿過磁場后都能垂直射到熒光屏MN上,熒光屏與y軸平行,求:(1)熒光屏上光斑的長度;(2)所加磁場范圍的最小面積.

圖3

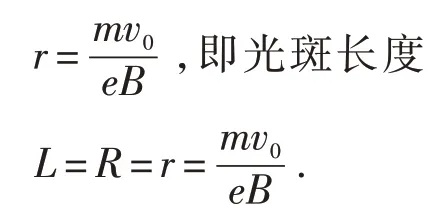

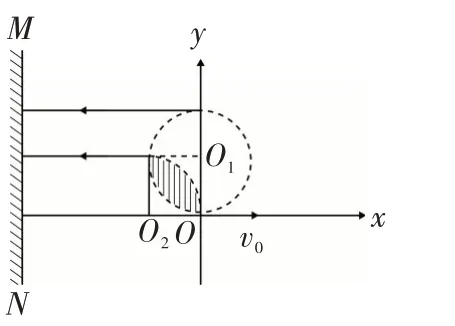
圖4



例3 如圖5所示,真空中有(r,0)為圓心,半徑為r的圓柱形勻強磁場區域,磁場的磁感應度大小為B,方向垂直于紙面向里,在y=r的虛線上方足夠大的范圍內,有方向水平向左的勻強電場,電場強度的大小為E,從O點向不同方向發射速率相同的質子,質子的運動軌跡均在紙面內,設質子在磁場中的偏轉半徑也為r,已知質子電量為e,質量為m,不計重力及阻力的作用,求:(1)質子射入磁場時的速度大小;(2)速度方向沿x軸正方向射入磁場的質子,到達y軸所需的時間;(3)速度方向與x軸正方向成30°角(如圖5)射入磁場的質子,到達y軸的位置坐標.要求畫出質子運動軌跡的示意圖.

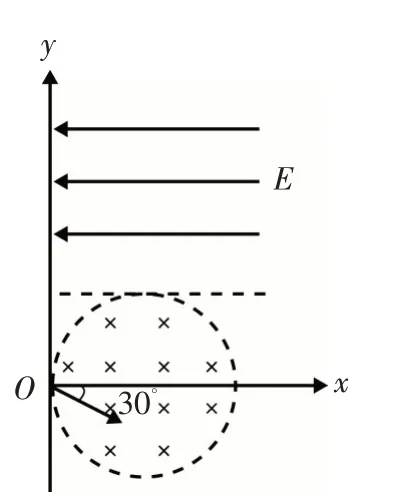
圖5
(2)根據結論1知,質子沿x軸正向射




圖6

例4如圖7所示,在第一象限內有沿y軸負方向的電場強度大小為E的勻強電場;在第二象限中,半徑為R的圓形區域內存在垂直紙面向外的勻強磁場,圓形區域與x、y軸分別相切于A、C兩點;在A點正下方有一個粒子源P,P可以向x軸上方各個方向射出速度大小均為v0、質量為m、電量為+q的帶電粒子(重力不計),其中平行于y軸正向射出的帶電粒子剛好從C點垂直于y軸進入電場.求:(1)勻強磁場的強度;(2)帶電粒子到達x軸上的范圍和帶電粒子到達x軸前運動的最長時間;(3)如 果 將第一象限內的電場方向改為沿x軸負向,粒子將從何處離開磁場?

圖7


圖8
(3)根據結論2知,粒子離開磁場的位置與第一象限電場無關,粒子將從D處離開磁場.
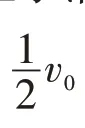
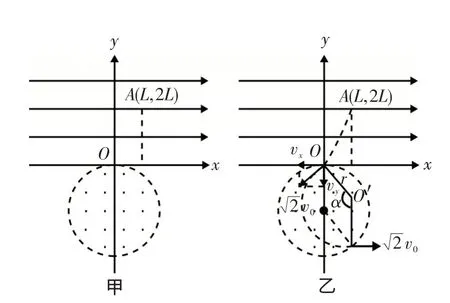
圖9


通過以上例題可以看出,當帶電粒子在圓形有界磁場中運動半徑等于軌跡圓半徑時,從磁場邊界上沿不同方向入射的相同粒子改變為沿相同方向射出;平行入射的相同粒子將會聚于同一點射出.可見,磁場圓好比一個凸透鏡,可以讓從焦點入射的光線改變為平行光線;也可以將平行光線會聚于焦點.我們把這種問題叫做“磁發散和磁聚焦”.利用好兩個結論能快速的解決此類問題,起到事半功倍的效果.

