楊氏模量測定儀器的創新與實踐

石長青，蔣 旭，李潔欣，羅 浩，陳俊冬，馬婷婷

(西南科技大學 ，四川 綿陽 621010)

楊氏模量是描述固體材料抵抗形變能力的物理量，也叫拉伸模量，1807年由英國物理學家托馬斯·楊所提出。由此便誕生了伸長法[1]、等厚干涉法[2]、雙縫干涉法[3]、衍射法[4]、液壓法[5]、電測法[6]等楊氏模量的測量方法，經調查發現傳統光杠桿拉伸法測定楊氏彈性模量[7]存在諸多誤差，如系統誤差(測量儀器上端自身存在的形變量導致實驗結果誤差較大、砝碼長時間的氧化腐蝕、金屬絲的搖晃)、偶然誤差(觀察者從不同角度透過望遠鏡觀察讀數也不同、實驗時難以找像)，創新點是將整個實驗裝置一體化，降低了實驗誤差，保證了實驗人員的安全，提高了測量精度并減少了煩瑣地找像步驟，節省大量實驗時間，使得實驗操作更加高效。

1 實驗原理

材料在彈性變形階段，其應力和應變成正比例關系，其比例系數稱為彈性模量[8]。通過激光發射器前端與標尺的距離，金屬絲與三角支架臺前端承載激光發射器的金屬桿之間的距離和讀數的改變量ΔD，可求出ΔL。

2 實驗裝置改進

圖1～圖3是實驗裝置圖。

圖1 實驗裝置總體圖

圖2 實驗裝置上部圖

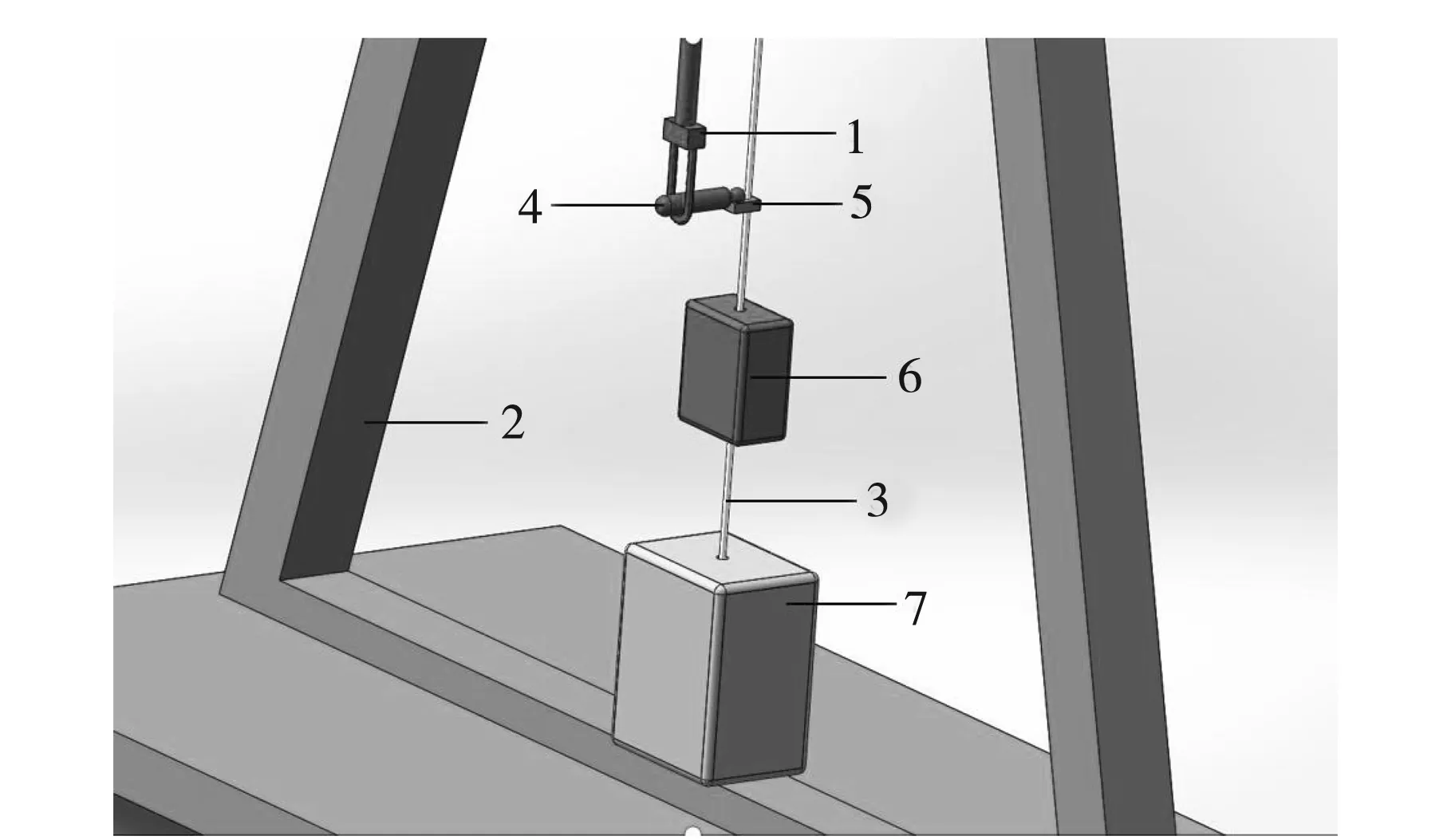
圖3 實驗裝置下部圖

2.1 實驗裝置介紹

2.1.1 儀器創新配件

1-金屬桿，其頂端固定在三角支架臺的上端，其下端用于放置激光發射器前端(可活動)。

2-三角支架臺，材質為鑄鐵、形變量小，且為三角穩定性設計，在底座平面嵌入水準儀輔助調平實驗裝置，確保實驗過程中金屬絲受力豎直。

3-金屬絲，用于實驗測定楊氏模量的金屬絲，材質為碳鋼。

4-激光發射器，其整體為圓柱外形，尾部為光滑球體結構，放置于金屬絲夾具打孔位置，激光照射到標尺上更加直觀地觀察到變化量，無須進行復雜地找像工作。

5-金屬絲夾具，該裝置有兩孔，大孔用于放置激光發射器尾部的光滑球體，使激光發射器尾部能夠自由地在孔中活動，小孔固定于金屬絲上，使其不在金屬絲上滑動。

圖4 金屬絲夾具圖

2.1.2 精準施力裝置[9]

6-力敏傳感器，其本身連接被測金屬絲末端和加力裝置，用于測量金屬絲豎直受力數值，使施力裝置施力更加精確。

7-施力裝置，固定在底座，用于控制金屬絲受力大小，電動控制，提高施力大小的準確度，減少外力對實驗裝置造成晃動等影響。

2.2 改進儀器優勢

2.2.1 儀器創新配件

①三角支架臺整體改善了現有傳統實驗裝置上端橫向形變造成誤差問題；②采用激光發射器去除了傳統實驗復雜的使用望遠鏡找像環節，節省大量實驗時間，操作更加便捷高效；③實驗裝置的一體化充分降低實驗裝置帶來的誤差，保證了能夠獲取高精度的實驗數據，減少了很多復雜的操作步驟，且實際搬運時更加方便。

2.2.2 精準施力裝置

精準施力裝置能夠更加精確高效地施加荷載，避免了傳統實驗操作時因砝碼搖晃所產生的誤差，保證了實驗人員的安全，同時也避免了因人員加載砝碼來回走動造成的振動對實驗引起的誤差。

3 改進后實驗步驟

(1)將三角支架臺運用水平儀調制水平，而后將金屬絲的一端固定在支架臺頂端，三角支架臺上的金屬桿長度為L1，金屬絲的總長度為L2，并在距離金屬絲端點的L3長度(實驗有效計算長度)處固定金屬絲夾具(L2>L3>L1)。

(2)打開激光發射器，通過激光調整平面鏡的位置，使其固定在三角支架臺前方適當的距離(1 m)的高度上，使標尺所在平面垂直于金屬絲、金屬桿和激光發射器所在的平面且平行于金屬絲和金屬桿。

(3)測量力和金屬絲伸長量的關系，為了消除彈性形變的滯后效應引起的系統誤差，采取“先測遞增荷載，再測遞減荷載”的實驗方式，以每次增減1 kg的等效力來消除誤差。

(4)為了避免開始測量時鋼絲未拉直這一問題，規定初始加載2 kg的等效力，讓初始激光直接照射到激光發射器前端的標尺上，并記錄初始數據R1。

(5)通過精準施力裝置使金屬絲的長度能夠隨著施加的精準力的變化而逐漸發生變化，同時讓金屬絲夾具水平高度也隨著變化，目的就是讓激光發射器后端的水平高度變化，而引起激光發生微小角度的偏轉，光線按照控制的路線照射到標尺上，依次記錄數據R2，R3，R4，R5，R6[2]。

(7)用螺旋測微器測量金屬絲加載前后的直徑D，共六次。

圖5 實驗原理圖

(8)首先計算出金屬絲與金屬桿的豎直距離M。

L3-L1=M

(9)再用米尺測出金屬絲與金屬桿間的距離長度N。

(10)最后通過測得R1、R2，兩者作差可得ΔR，與已知的標尺到平面鏡的距離可通過數學原理求出OR1的長度；求得的M與N通過數學原理可得OL3的長度；最終運用數學原理可得出ΔL。

(11)根據胡克定律等與上面一系列公式的轉化得出下列計算式，用逐差法處理數據，計算實驗結果。

4 改進后的實驗結果及數據處理

(1)測量金屬絲受力后的變形量ΔL

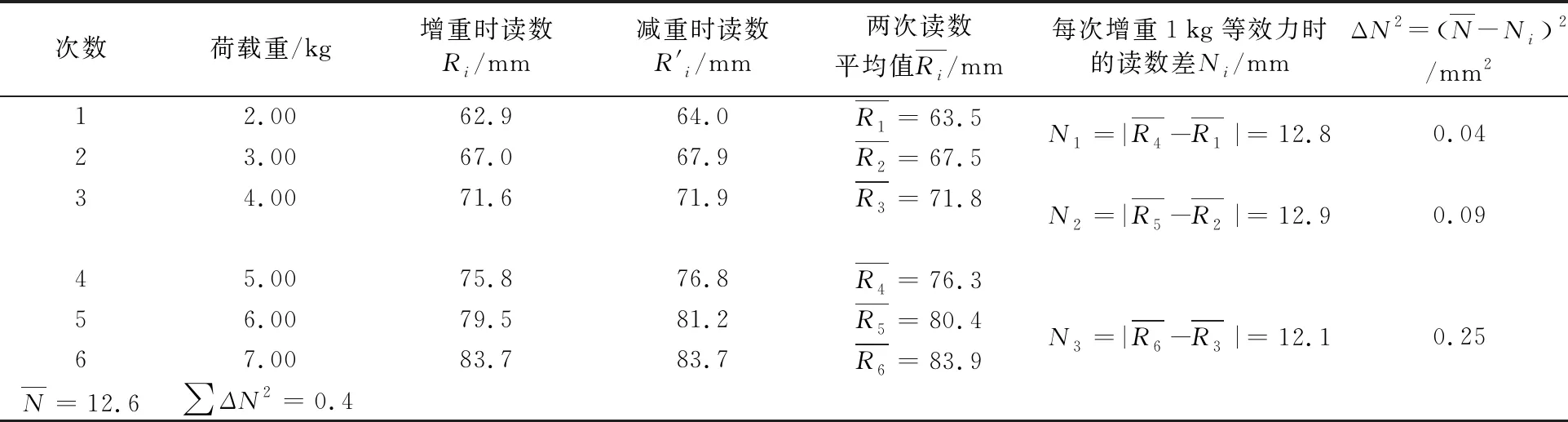
表1 增減荷載時標尺讀數(單位：mm)

(2)測量金屬絲直徑

表2 金屬絲直徑

(3)測量金屬絲計算長度L3

儀器上端到金屬絲夾具間金屬絲長L3=698 mm

(4)測量計算出M、N

M=L3-L1=698 mm-545.9 mm=152.1 mm

N=450 mm

(5)計算楊氏模量Y及其標準不確定度

將上述所得數據代入計算公式得：

計算Y的標準不確定度：σY=Er

實驗使用的金屬絲材料為碳鋼，在20 ℃時楊氏模量的理論值應在2.0×104～2.1×104范圍內，因此設計的儀器創新方案得到了充分的證實。

5 結 語

實驗采用三角支架臺與激光發射器測量金屬絲的楊氏彈性模量，測量中需綜合多種測量工具與計算方法，使楊氏模量測量數據更精準、操作過程更方便、更穩定，確保了一定的精度要求。

(1)通過三角支架臺的穩定性和一體化減少系統誤差，隨著荷載的變化導致激光發生微小角度的偏轉，照射到標尺上更加直觀地觀察到變化量(將求鐵絲的長度變化量間接轉化為求激光光點照射到標尺上的位移量)。

(2)同時將傳統實驗復雜的望遠鏡找像替換成激光發射器成像，師生更加容易上手操作，節省了大量實驗時間，并通過數學原理計算出真實變化量，從而根據相應計算式測定楊氏模量。

(3)儀器既增強了學生創新思維和動手能力，又為儀器廠商和教育單位創造更大的效益，具有較高的實用價值。

(4)在工程上(建筑交通、水利設計等) 對研究結構受力、分析結構穩定性等起到重要作用，并且響應了教育部建設中國金課號召。