南海地區巖石圈有效彈性厚度估計

龔 正 李志剛 胡立天 熊建國 孫 闖

1 中山大學地球科學與工程學院廣東省地球動力作用與地質災害重點實驗室，廣州市新港西路135號，510275 2 南方海洋科學與工程廣東省實驗室(珠海)，廣東省珠海市港灣1號，519080 3 中國地震局地質研究所地震動力學國家重點實驗室，北京市華嚴里甲1號，100029

巖石圈有效彈性厚度(Te)是指與巖石圈板塊中實際應力產生的彎矩相等的理論彎曲彈性薄板的厚度[1-2]，是一個描述巖石圈在地質時間尺度下的強度指標[3]，對于探討巖石圈的動力學模型和構造運動有重要作用，通常通過重力異常和地形在頻域中的相關性計算得到[4]。20世紀90年代之前，研究者利用互相獨立的船載重力觀測和船載地形觀測數據計算有效彈性厚度[5-6]，但鑒于船測資料往往與測線的選擇密切相關，其反映的僅是測線段上的有效彈性厚度值。隨著衛星技術的發展，人們可以在全球進行地形和重力觀測，從而計算大區域和全球尺度的巖石圈彈性厚度，不過測高衛星資料常被同時應用于全球地形模型和全球重力場模型中[7-8]，可能會對地形和重力的相關性產生影響，從而影響有效彈性厚度的估計。

考慮到在張裂構造背景下構造單元的變形程度與巖石圈強度密切相關[9]，計算南海地區的有效彈性厚度能進一步了解整個區域的巖石圈強度，并有助于理解該區域的構造演化過程。本文以南海地區南沙群島為例，分析測高衛星資料對計算有效彈性厚度的影響，并計算南海地區有效彈性厚度的分布，結合巖石圈年齡分析計算結果的含義。

1 計算方法與數據

1.1 巖石圈Te計算基本原理

巖石圈有效彈性厚度的計算通常采用導納法和相關性法等譜分析方法，在海洋區域一般采用導納法[10]。該方法對重力異常和海底地形進行譜分析，計算兩者之間的導納關系，即實測導納Z，將計算結果與巖石圈Te取不同值時根據模型計算得到的理論導納Z′進行比較，當兩者之差的均方根最小時獲得Te的計算結果。

巖石圈Te由撓曲均衡理論確定[3]，具體計算原理見文獻[11]。可以看出，導納法計算Te需要重力、地形及地殼結構等信息。

1.2 計算南沙群島Te的數據及參數設置

南海地區(10°S～30°N，90°E～130°E)重力觀測資料豐富，有不少學者利用各種方法和資料計算了南沙群島的有效彈性厚度[12-14]，但普遍沒有考慮測高衛星對數據資料的影響。作為構造活動相對穩定的區域，在計算Te時可將南海地區作為一般的加載模型，根據前人經驗，這種條件適合采用導納法進行Te計算[15]。

為對比測高衛星資料的影響，分別采用由測高衛星資料和重力資料聯合得到的重力場模型(WGM2012)[16]及完全由重力衛星得到的重力場模型(ITU_GGC16)[17]計算Te，計算所需的地形模型選擇由船測資料和測高衛星共同得到的GEBCO模型[18]。本文重力模型在南海地區的重力異常和地形如圖1所示，可以發現，地形與重力異常存在對應關系，越陡峭的區域重力異常越顯著，這是一般加載模型的典型特征。

圖1 南海地區的重力異常和地形Fig.1 The gravity anomaly and the topography in the South China Sea

Clift等[19]在南沙群島(8°N～13°N，111°E～116°E)附近使用地質模擬方法來估算巖石圈的Te，其基本思路是應用不同的Te正演模擬長時間以來(28 Ma)海底地貌沉積的分布與厚度，并將其與當前地震反射剖面得到的地殼結構作對比，估算得到南沙群島的Te值為8～10 km。考慮到該方法與本文計算Te的思路完全不同，可以作為一個互相印證的指標。

在計算研究有效彈性厚度時還需涉及該區域的地殼模型參數，包括地殼分層厚度、每層密度、楊氏模量及泊松比等。為此，選擇現有分辨率最高(1°×1°)的全球地殼模型crust1.0模型[20]作為這些參數的來源(表1)，其中海水、地殼和地幔密度分別為模型在研究區域的平均值，平均水深為模型提供的平均值。

表1 研究區域的部分地殼參數

2 計算結果及分析

2.1 南沙群島Te的計算和分析

首先計算南沙群島的Te(圖2)，并與前人研究成果[12-14, 19, 21-22]進行對比(表2)。

通過擬合發現，南沙群島地區利用ITU_GGC16模型計算時的最佳Te為9.1 km，最佳擬合時的均方根為5.3 mGal/km(圖2(a))；利用WGM2012模型擬合時的最佳Te為9.3 km，最佳擬合時的均方根為6.1 mGal/km(圖2(b))。采用聯合的重力場模型比采用重力衛星的重力場模型計算的Te要高約2%；而采用2種數據計算的最小均方根在5～6 mGal/km，兩者的擬合情況都比較好。需要說明的是，由于ITU_GGC16模型受空間分辨率的限制，僅使用波長在250～1 000 km的部分進行擬合。考慮到采用WGM2012模型可能會高估有效彈性厚度，本文認為利用ITU_GGC16模型計算得到的Te比利用WGM2012模型計算得到的Te更準確。

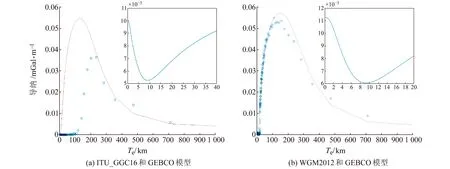
圖2 兩種模型的最佳擬合Te及相應的RMSFig.2 The best fitting Te of two models and their RMS

表2 南沙群島Te研究對比

與前人的計算結果對比發現，南沙群島Te的計算結果有一定的差異，即使使用同類方法，因為應用的算法參數和采用的數據及地殼模型不同，結果也存在一定差距。總體來看，除了Tesauro等[22]的結果，其他研究的Te值都在4～20 km的區間范圍內，其中同樣應用導納法計算Te的蘇達權[12]采用的海底地形模型(Sandwell模型)由測高衛星反演得到，應用相關性法的Shi等[13]采用的模型組合與本文的WGM2012+GEBCO組合類似，也存在重力模型與地形模型不互相獨立的問題，其結果都比本文結果稍高，可能高估了實際的有效彈性厚度。考慮到Clift等[19]采用的地質模擬法與本文方法在數據和思路上均不相同，但結果較為接近，證明本文計算結果比較可靠。

總體來看，在南沙群島地區計算有效彈性厚度時重力模型是否包含測高衛星資料對計算結果存在一定的影響，測高衛星資料未重復應用在重力模型和地形模型中的計算結果要小于重復應用的情況。

2.2 南海Te分布計算和分析

進一步計算南海地區(圖3(a))的Te分布，計算時采用多窗口法[23-24]，選擇一個800 km×800 km的滑動窗口，并以50 km的間隔滑動，最后平滑得到1°×1° 的有效彈性厚度分布。§2.1的結果表明，在計算有效彈性厚度時，如果在重力模型和地形模型中重復使用測高衛星資料可能高估該值，所以在計算Te分布時采用GEBCO地形模型，重力模型采用不包含測高衛星資料的ITU_GGC16模型。為減少干擾，去掉陸地部分的有效彈性厚度結果，僅看海洋部分，將南海海盆地區(0°～25°N，95°E～125°E)作為分析重點并放大(圖3(b))。

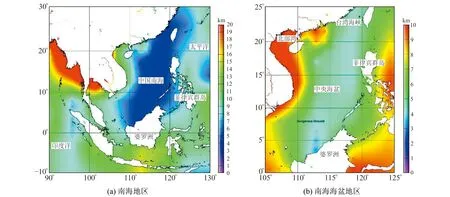
圖3 有效彈性厚度分布Fig.3 The Te distribution

可以看出，南海地區的Te值顯著低于周邊區域，基本在3～8 km的區間范圍，而南海中央海盆地區的Te值約為4 km，相比之下南海周緣的Te值稍大。東北部臺灣海峽附近和靠近菲律賓群島處均為7 km左右，中央海盆西側的Te值從7 km一直上升到北部灣地區的10 km。南部靠近婆羅洲地區存在Te值銳減至4 km的區域，但在南海之外的地區Te值整體較大，東側的菲律賓海溝處Te值為10～15 km，南側越過婆羅洲的區域能達到16 km，這也是除了印度洋除靠近青藏高原的部分外Te值最大的區域。

根據全球巖石圈年齡模型[25](圖4)對比南海地區的巖石圈Te可以發現，最小Te的南海海盆對應著最年輕的巖石圈，符合南海海盆的擴張歷史；印度洋北部和印尼地區有較大的Te，對應巖石圈相對古老的年齡。菲律賓海溝的西側為Te較小的區域，而海溝東側的Te顯著增大，這也與巖石圈的年齡相對應。總體來看，在海洋或者洋殼區域，有效彈性厚度的分布與巖石圈年齡的分布比較一致。

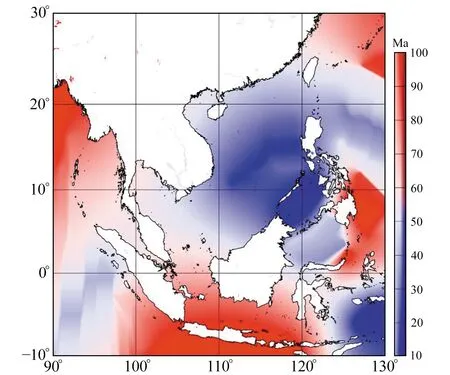
圖4 南海地區巖石圈年齡分布Fig.4 The lithosphere age distribution in the South China Sea

3 結 語

本文利用2種不同的數據組合計算了南海地區南沙群島的巖石圈有效彈性厚度，分析了重力模型及地形模型均來自衛星測高數據時對計算結果的影響，同時計算了南海地區的有效彈性厚度分布，并與南海地區的巖石圈年齡進行對比，通過對計算結果的分析得出以下結論：

1)在計算有效彈性厚度時，如果重力模型和地形模型都應用了測高衛星資料，會導致重力模型和地形模型不互相獨立，從而高估有效彈性厚度值，在南沙群島地區的高估影響約為2%。

2)雖然ITU_GGC16重力模型的空間分辨率低于WGM2012模型，但由于有效彈性厚度反映的是長波段的巖石圈信息，ITU_GGC16重力模型的波段能夠有效覆蓋從而得到準確的有效彈性厚度值。

3)對比前人計算得到的南沙群島有效彈性厚度值，本文得到的約9 km的結果與同類方法的結果相近，與思路不同的地質模擬法的計算結果也比較接近，所以認為9 km的有效彈性厚度值結果是可信的。

4)南海地區巖石圈的有效彈性厚度分布表明，南海地區有效彈性厚度在0～15 km之間，南海海盆的有效彈性厚度最小(可以達到4 km)，北部灣地區的有效彈性厚度相對較大(可以超過10 km)。總體來看，南海周邊區域的有效彈性厚度值普遍比南海地區大，印尼周邊區域、印度洋北部和菲律賓海溝東部部分地區存在較大的有效彈性厚度，能達到10～20 km。

5)南海地區的有效彈性厚度與海底巖石圈年齡的空間分布有較強的相關性，這與前人的研究結論一致。南海海盆的有效彈性厚度小于周緣地區的有效彈性厚度，這也符合南海海盆的擴張歷史。