復合材料飛機接地回流網絡建模與阻抗分析

劉建英，隋政，張起浩，楊占剛

(中國民航大學 電子信息與自動化學院，天津300300）

大規模使用復合材料是現代飛機發展的一個重大趨勢，復合材料用量是當今全球航空業衡量飛機先進性的重要指標［1-2］。與傳統的金屬材料相比，先進的復合材料對于飛機的減重、增加強度、耐腐蝕、簡化維護都大有益處，但相應地也會在飛機電力系統的接地系統設計方面帶來一系列問題。傳統的全金屬機身導電性能優良，在飛機電力系統的接地系統設計時可將其視作理想的接地平面，但復合材料機身的導電性能與傳統全金屬機身相差較大，將極大影響整機的電氣性能［3-5］。基于此，美國聯邦航空管理局(Federal Aviation Administration，FAA）關于飛機接地防護手冊和咨詢通告中提出，復合材料結構的飛機應為電源電路設置獨立的電源回流走線，如碳纖維復合材料(Carbon Fiber Reinforced Plastic，CFRP）機體就需提供接地回流網絡供電流流通。

在接地回流網絡各性能參數中，阻抗是最不可忽略的參數之一。飛機上接地結構必須具有足夠低的阻抗值，使得電流回路上的電壓降可以忽略不計［6］。由于接地回流網絡不可能是完全理想的接地平面，其性能很可能比目前在金屬飛機上的接地性能更差［7-8］。如果發生接地故障，故障電流可能會通過復合材料到達接地回流網絡，從而影響機載用電設備性能。對復合材料與金屬電流回流網絡搭接的阻抗進行計算有利于接地或搭接的實施，以及適當的故障管理和電氣保護系統設計［9］。

目前，針對媒質體阻抗計算的主流方法包括有限元法(Finite Element Method，FEM）、矩量法(Method of Moments，MoM）、部 分 元 等 效 電 路(Partial Element Equivalent Circuit，PEEC）法等。有限元法基于麥克斯韋方程的微分形式，將空氣和其他所有材質分割成小尺寸單元，假設每個單元內部的場為常數，使用變分技術求解麥克斯韋方程組，對硬件要求高、速度慢，適用于小尺寸模型的計算［10-11］。文獻［12］提出了基于有限元法的半解析方法，計算鐵路軌道阻抗并應用于鐵路信號電路系統，相關算例應用在較低的頻段并對方法進行了優化，但對于高頻段的應用具有一定局限性。矩量法基于麥克斯韋方程的積分形式，將導體分成小尺寸單元，通過計算所有導體單元上的電流，得到所有導體電流單元總體產生的電磁場，具有較高的計算精度和相對較少的未知數，但計算速度依然較慢［13-14］。文獻［15］基于矩量法，在邊界積分方程的基礎上提出了等效表面阻抗模型，并通過算例驗證了方法的有效性，但相關算例對象主要應用于小尺寸的集成電路。文獻［16-17］對矩量法做了一些改進，但所采用的優化算法仍使計算過程較為復雜。

PEEC法基于電場積分方程，由離散結構中的電流和電荷間的相互作用，引入部分元件的概念建立電氣連接得出等效電路［18-21］。PEEC法本質是通過對電場積分方程進行等效電路的離散化，將電磁結構的各種電磁效應轉化為對應的等效電路模型中的集總電路元，如電阻、電感、電容、受控源等，適合用于信號完整性分析的互連和封裝結構的建模，可以在提高算法效率的同時保持計算精度［22-25］。歐盟委員會“Clean Sky Joint Undertaking”項目開發了一套基于數值算法的仿真工具，來模擬安裝在復合材料飛機上的電流回流網絡，并利用表面PEEC法對構成網絡本身的不同部分阻抗建立一個精確的模型［26］，但未考慮復合材料及相關參數對金屬結構阻抗的影響。本文采用PEEC法對包括金屬導軌和復合材料蒙皮的接地回流網絡進行建模，考慮接地回流網絡的不同結構、參數及不同接地點，計算接地回流網絡在不同參數、結構下的阻抗，并分析影響接地阻抗的因素。

1 部分元等效電路法

在導體中任一點r處施加外部電場，頻域電場積分方程為

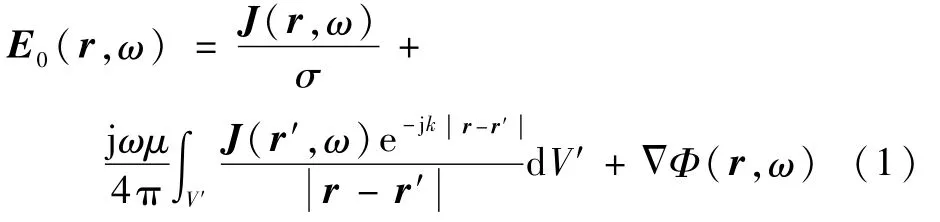
式中：μ為磁導率；V'為導體體積，此處在導體體積V'上積分；σ為導體的電導率；J(r，ω）為體積電流密度，r表示導體中的任一點；ω為角頻率；E0(r，ω）為外部源輻射的入射電場；r'為單元的中心點；k=ω/c0為波數，c0為真空中的光速；Φ(r，ω）為電標量勢，與電荷分布有關，即

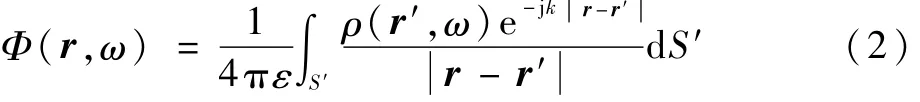
其中：ρ(r'，ω）為表面電荷密度；ε為材料介電常數。

在PEEC建模中，電流密度滿足連續性方程：

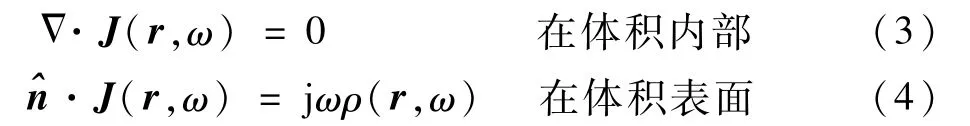
在立方體的內部和表面對體積進行離散，進而得到方程組。

用一組基函數fn(r）和gm(r）的加權和，對體積電流和表面電荷進行計算：

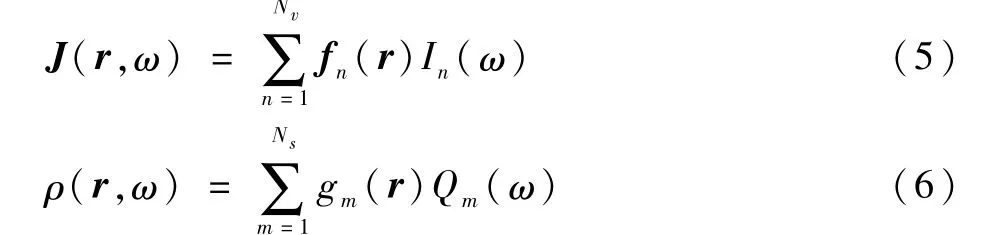
式中：fn(r）、gm(r）為每個角頻率下的基函數；In(ω）和Qm(ω）為相應的加權函數；Nv和Ns分別為體積基函數(或體積單元）和表面基函數的數量。

將式(5）、式(6）代入式(1）、式(2）得

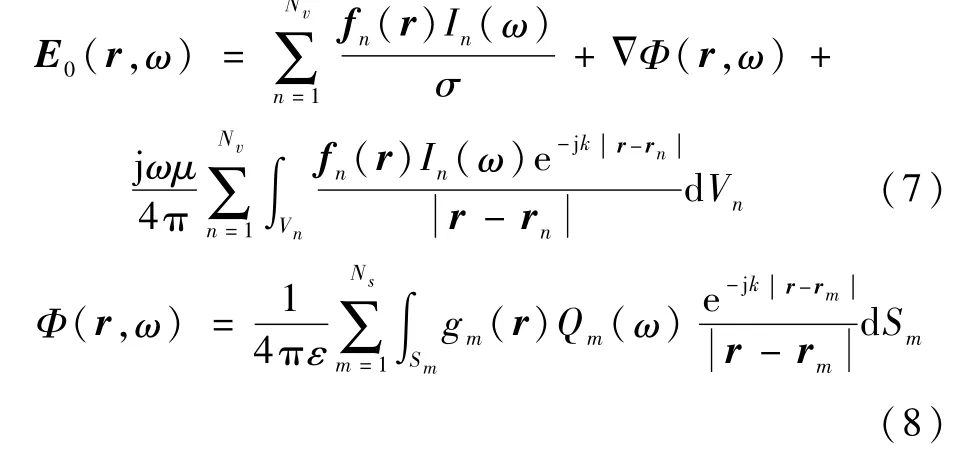
式中：rn表示第n個體積單元的中心；rm表示第m個表面單元的中心。

用Ritz-Galerkin方法，令方程(7）、方程(8）的殘差與一組加權函數正交，生成未知的加權函數In(ω）(n=1，2，…，Nv）和Qm(ω）(m=1，2，…，Ns）。

采用分段常數函數作為加權函數，將要處理的正交導體的表面離散為Ns個基本矩形片。在離散模型中，假設每個單元上未知電流和電荷密度為恒定值，則用于擴展電荷密度的基函數為

計算每個矩形片上Φ(r，ω）的平均值為

定義Plm(ω）為電勢系數，因此，Ns個矩形片上的電勢和電荷在角頻率為ω時具有如下關系：

矩陣P稱為電勢系數矩陣，與頻率有關，與位移電流Ic(ω）有如下關系：

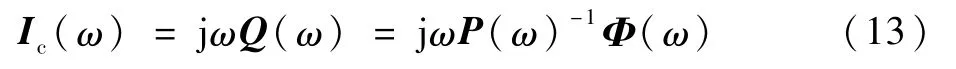
將導體的體積離散為Nv個基本正交六面體，并假設E0(r，ω）在每個體積中是均勻的，用于擴展電流密度的基函數選擇為

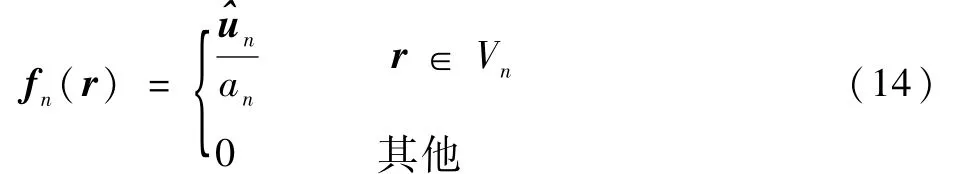
將fn(r）代入式(7），應用Ritz-Galerkin方法，計算每個體積單元E0(r，ω）的平均值為

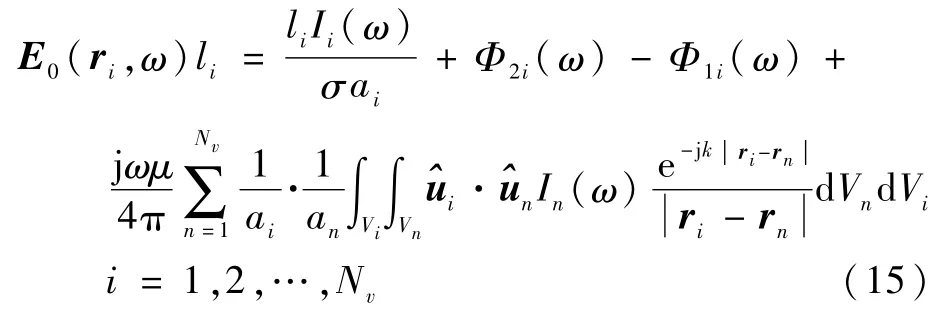
式中：Φ1i(ω）和Φ2i(ω）為體積Vi沿^ui方向的端電勢，Φ2i(ω）-Φ1i(ω）為體積Vi沿^ui方向的電勢差；li為第i個單元的長度。

定義部分電感為

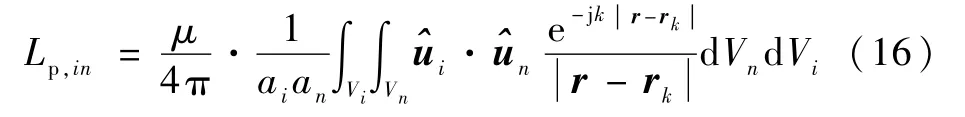
則式(15）可以寫為

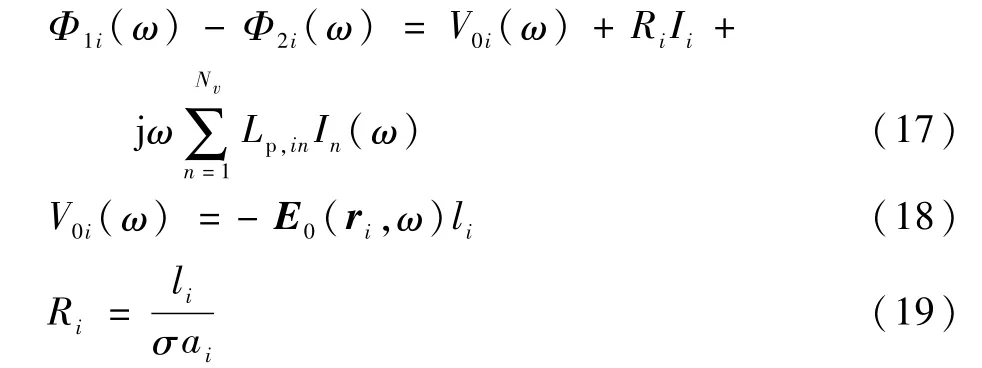
將式(17）寫成緊湊形式為

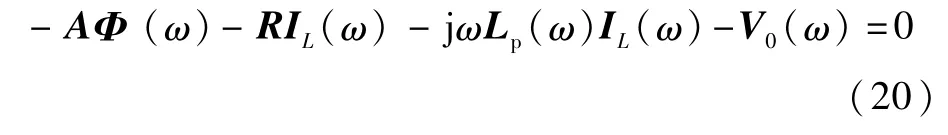
此即KVL在等效電路中的應用。式中：R為對角矩陣，表示每個基本六面體的電阻；IL為流過部分電感上的電流；Lp(ω）為描述磁場的部分電感矩陣；V0(ω）為產生的入射場分布效應的縱向電壓源和最終集總的電壓源；A為鄰接矩陣，取值為

對連續性方程積分得到

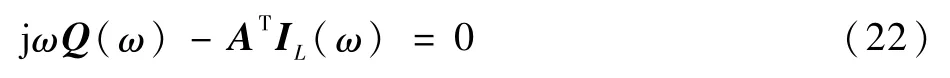
考慮外部電流源I0(ω），并將式(13）代入式(22）得

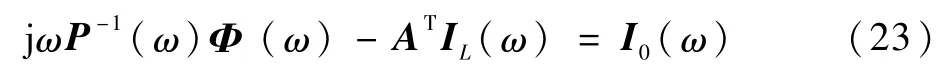
聯立式(20）、式(23）得頻域求解器為

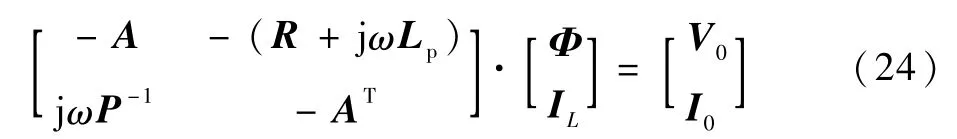
對于電介質，建模時需要考慮體積極化電流，麥克斯韋位移電流方程寫為

式中：E為電場強度；ε0為真空中的介電常數；ρF和ρB分別為自由電荷密度和束縛電荷密度。

令總電荷密度ρT=ρF+ρB，考慮極化電流后的總電流密度為JT(r，ω），寫為

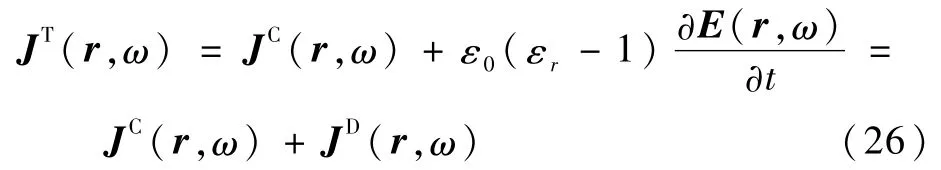
式中：JC(r，ω）為導體電流密度；JD(r，ω）為電介質的電流密度。

對于介電常數為εr的區域內任一點，電場積分方程為

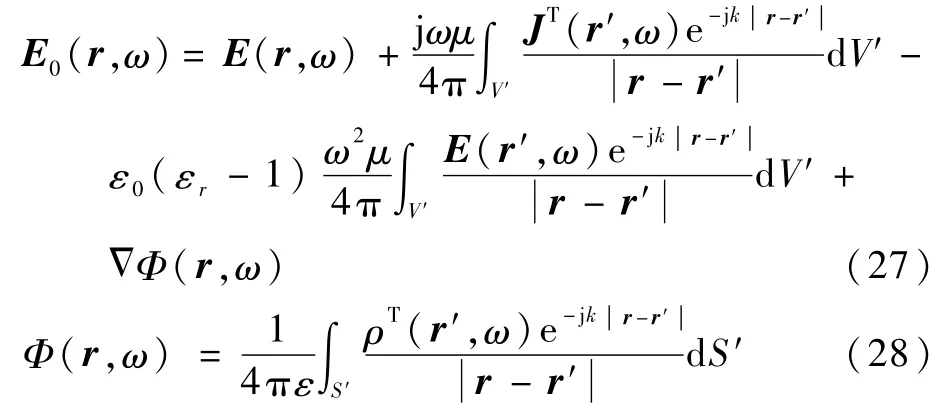
同理，由式(24）得電介質材料CFRP等效電路的頻域求解器為

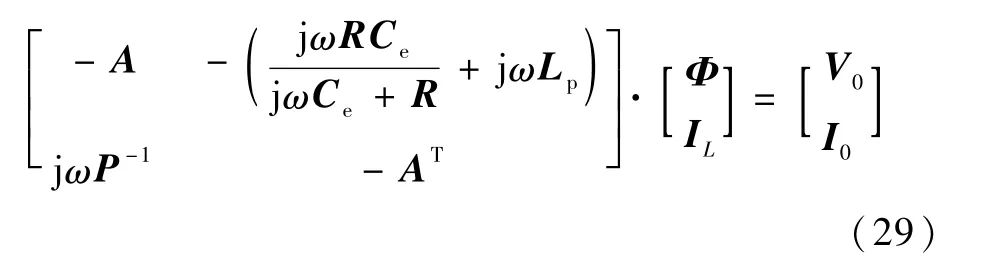
式中：Ce=ε0(εr-1）ar/lr為殘余電容，ar和lr分別為體積單元的截面積和長度。

2 接地回流網絡結構建模

2.1 復合材料飛機接地回流網絡結構模型

復合材料飛機接地回流網絡主要由金屬導軌和復合材料蒙皮搭接而成，金屬導軌由鋁制成，機身復合材料通常為CFRP。以1塊復合材料板和4根金屬導軌搭接成的接地回流網絡模型作為研究對象(見圖1），來模擬金屬導軌與復合材料蒙皮間的搭接。以導軌端口1、2間的阻抗為例，計算金屬接地回流網絡在不同參數、結構下的阻抗。

圖1中各結構材料的相關電磁參數設置如表1所示，各部件外部尺寸參數如表2所示，金屬導軌的截面積為600 mm2。

圖1 復合材料蒙皮與金屬接地回流網絡搭接模型Fig.1 Overlap model of composite material skin and metal grounded return network

表1 材料對應電磁參數Table 1 Electromagnetic parameters of materials

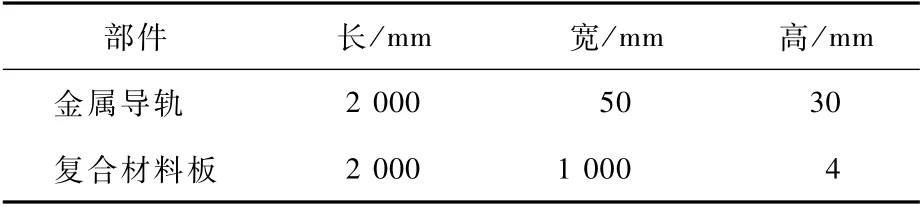
表2 部件外部尺寸Table 2 External dimensions of components

2.2 復合材料飛機接地回流網絡PEEC模型

根據體積內部剖分體單元為長方體、體積表面剖分面單元為長方形的剖分原則，進行網格劃分，針對如圖2所示的2個相鄰導體單元建立PEEC模型，根據式(23）和式(26）中各元件之間的數值關系，得到2個相鄰導體單元的部分元等效電路，如圖3所示。

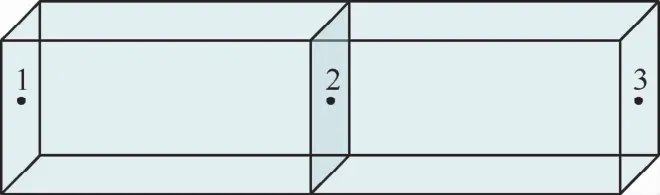
圖2 經過網格劃分后的2個相鄰導體單元示意圖Fig.2 Schematic diagram of two adjacent conductor elements after meshing

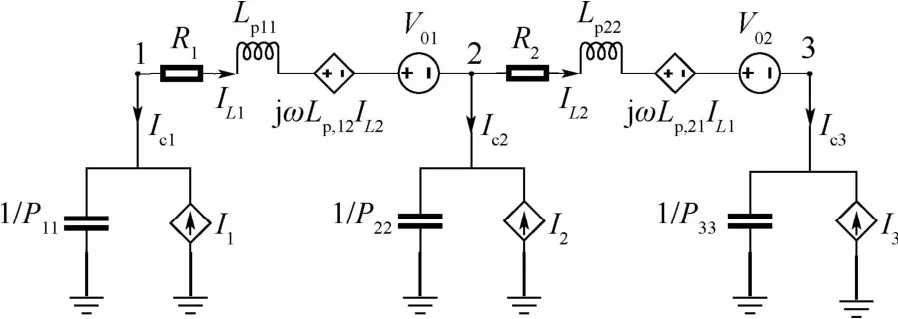
圖3 兩個相鄰導體單元的PEEC等效電路Fig.3 PEEC equivalent circuit of two adjacent conductor units

CFRP電阻率并不是特別高，不能稱為絕緣體，但能發生極化過程。考慮體積極化電流，相應的等效電路如圖4所示。

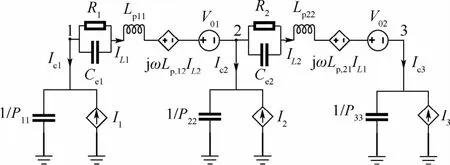
圖4 兩個相鄰電介質單元的PEEC等效電路Fig.4 PEEC equivalent circuit of two adjacent dielectric units

3 可行性驗證

以圖1中金屬鋁導軌作為驗證模型，導軌長2 m，厚度均勻，截面形狀為工字形，各部分尺寸如圖5所示。

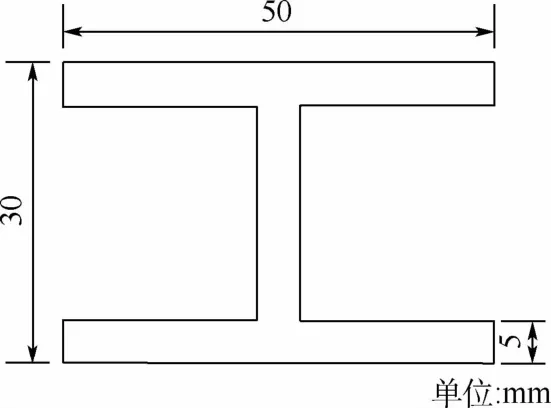
圖5 金屬導軌截面形狀及尺寸Fig.5 Cross-sectional shape and size of metal bar

對導軌進行相同的網格剖分，最高頻率設置為1 MHz，分別運用PEEC法、矩量法、有限元法3種方法計算導軌兩端的阻抗，在相同硬件條件下耗時分別為700 s、1 000 s、1 900 s，實部計算結果如圖6所示。

根據公式R=δl/s計算直流電阻值，δ、l、s分別為材料電阻率、長度、橫截面積，得其直流電阻值約為R=8.841 7×10-5Ω，該值與3種方法在頻率為0時的計算結果一致。圖6計算結果表明，在低頻段(f＜104Hz）時，3種方法的計算結果具有較好的一致性，但隨著頻率的增大，集膚效應使得導體有效截面積減小，交流阻抗值逐漸增大。PEEC法與有限元法和矩量法在高頻段的計算結果近似，但計算速度明顯較快。綜合來講，PEEC法在計算精度和速度方面具有一定的優越性。

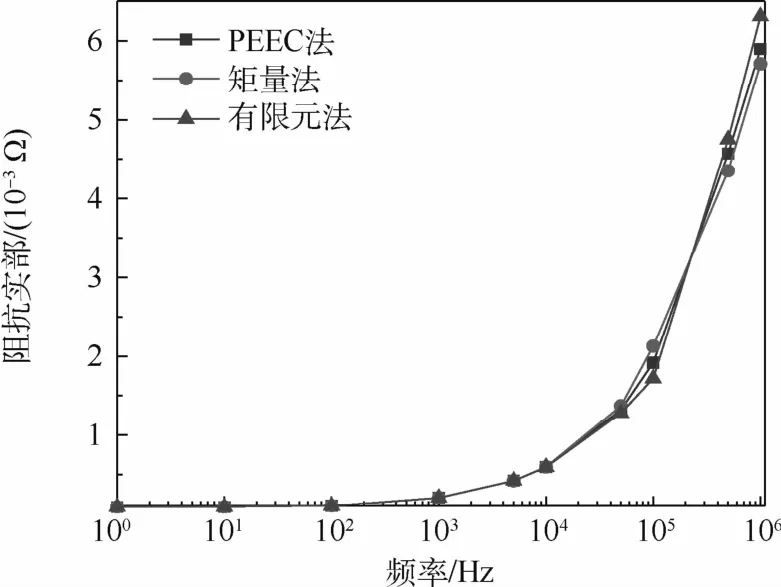
圖6 三種方法計算結果對比Fig.6 Comparison of calculation results among three methods

PEEC法計算出的金屬導軌直流電阻值、阻抗實部值、電抗值及阻抗模值分別如圖7所示。

通過將圖7中計算結果與文獻［27］進行對比，阻抗各部分計算值基本一致，驗證了方法的適用性及仿真結果的正確性。

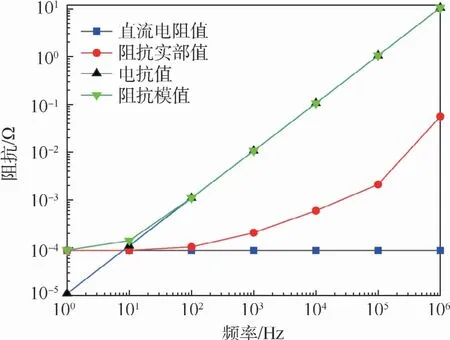
圖7 金屬導軌阻抗計算結果Fig.7 Calculation results of metal bar impedance

4 接地回流網絡阻抗計算

為了研究搭接復合材料蒙皮電導率及金屬導軌截面形狀對接地回流網絡阻抗的影響，將仿真項目分成4組，相關參數設置如表3所示。

表3 仿真項目及相關參數設置Table 3 Simulation project and related parameter setting

4.1 復合材料蒙皮對接地回流網絡阻抗的影響

對等效電路進行計算，當頻率為0時，圖1中金屬導軌接地回流網絡不搭接復合材料蒙皮時，算得導軌端口1、2間的阻抗值約為7.737×10-5Ω。根據公式R=δl/s計算直流電阻值，得導軌端口1、2間的直流電阻值為3.5R=7.736 5×10-5Ω，公式計算結果與PEEC法計算結果接近相等，且與文獻［27］中直流電阻值計算結果一致，再次驗證了方法的正確性。對比金屬導軌接地回流網絡搭接復合材料蒙皮前后相同導軌端口間的計算值，結果如圖8所示。

圖8計算結果表明，隨著頻率的升高，金屬導軌搭接復合材料蒙皮在一定程度上增大了端口間的交流電阻值，阻抗模值在金屬導軌搭接復合材料蒙皮后略有減小。

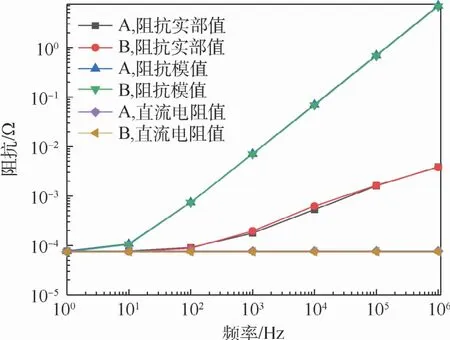
圖8 搭接復合材料蒙皮前后阻抗計算結果Fig.8 Impedance calculation results of overlapped and non-lapped composite material skin

4.2 復合材料電導率對接地回流網絡阻抗的影響

將圖3中復合材料蒙皮的電導率減小為2 000 S/m，其他條件不變，計算導軌端口1、2間的阻抗值，并于復合材料蒙皮電導率為20 000 S/m時作對比，結果如圖9所示。

圖9計算結果表明，減小搭接復合材料蒙皮的電導率，高頻時交流電阻值有所增大，阻抗模值也相應增大。

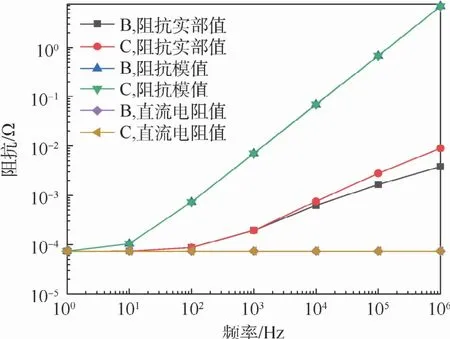
圖9 搭接不同電導率的復合材料蒙皮的阻抗計算結果Fig.9 Impedance calculation results of overlapped composite material skin with different conductivity

4.3 金屬導軌截面形狀對接地回流網絡阻抗的影響

將圖3中工字形金屬導軌截面改為同等面積的正方形，其他條件不變，計算導軌端口1、2間的阻抗值，并與工字形截面金屬導軌作對比，結果如圖10所示。

從圖10中結果可以看出，由于項目B、D中金屬導軌的截面積和搭接的復合材料蒙皮電導率相同，得到的導軌端口1、2的直流電阻值也完全一致，這與公式計算結果及相關電路原理相符合，且正方形截面的金屬導軌阻抗明顯比工字形截面大。

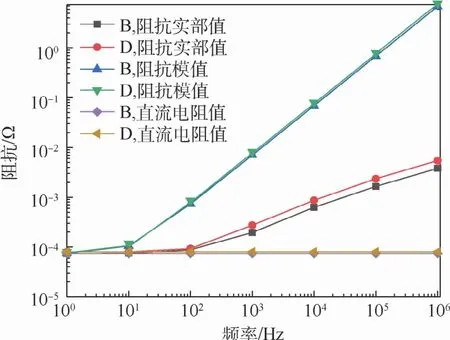
圖10 不同截面形狀金屬導軌的阻抗計算結果Fig.10 Impedance calculation results of different cross-sectional shapes of metal bar

為了更直觀地表示不同參數對接地回流網絡阻抗的影響，將頻域阻抗模值列出，如表4所示。

表4中阻抗模值的計算結果表明，金屬導軌搭接復合材料蒙皮會使接地回流網絡1、2節點間阻抗值略有減小；復合材料蒙皮電導率的減小會增大相應的阻抗值；相同條件下正方形截面導軌比工字形截面導軌的阻抗值大。

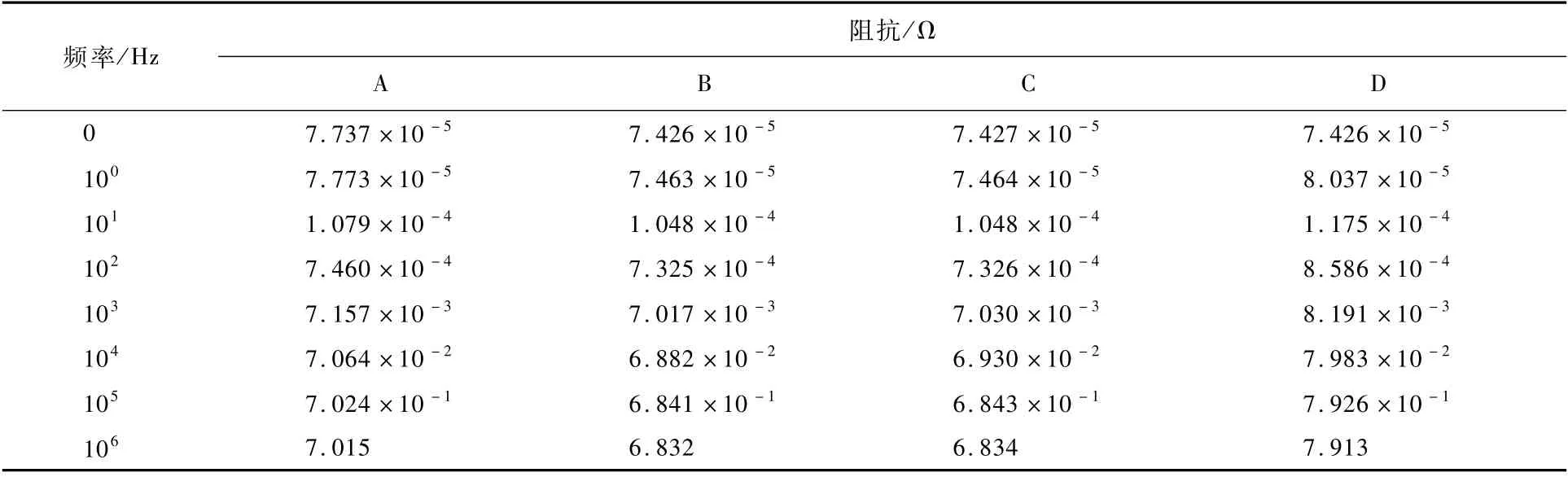
表4 不同參數設置下的節點間阻抗值Table 4 Impedance between nodes under different par ameter settings

5 接地回流網絡不同接地點間阻抗

將8塊長、寬、厚分別為20000 mm、2 000 mm、4 mm的復合材料板拼接成的筒狀結構，用來模擬飛機蒙皮的大致形狀。座艙底部鋁制接地回流網絡是由20個圖1中井字形網格拼接而成，總長為20 m，寬為4 m。其中，金屬導軌之間、復合材料蒙皮之間及金屬導軌與復合材料蒙皮之間均進行了良好的電氣連接。整體搭接模型如圖11所示。

為了清晰地表示不同節點，將圖11接地回流網絡進行編號，縱向4根長導軌分別標為a、b、c、d，橫向20根短導軌分別記為1，2，…，20。整個接地回流網絡共80個節點，每個節點均有各自的編號，如a1表示導軌a與導軌1之間相交產生的節點，b1表示導軌b與導軌1之間相交產生的節點，定義a1b1為兩節點間的阻抗。

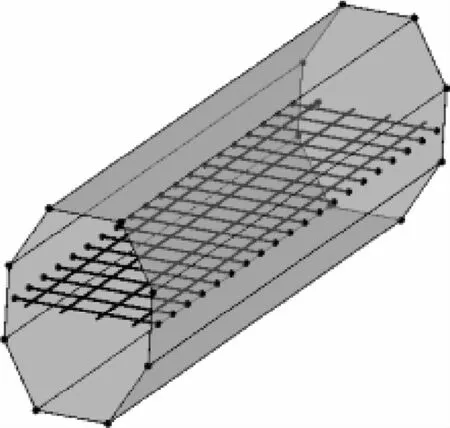
圖11 復合材料蒙皮與接地回流網絡搭接模型Fig.11 Overlap model of composite material skin and grounded return network

由于節點數量較多，在計算節點間阻抗前對其進行分類，將所有節點分為邊界節點和內部節點。如圖12所示，虛線內的節點為內部節點，虛線外的節點為邊界節點。

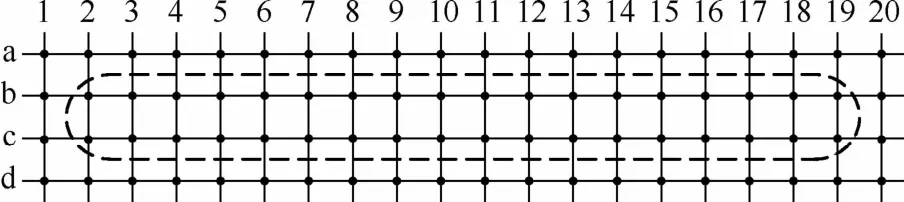
圖12 接地回流網絡平面示意圖Fig.12 Schematic diagram of grounded return network

相應的，將節點間阻抗分成3類，分別為邊界節點與邊界節點間的阻抗、邊界節點與內部節點間的阻抗、內部節點與內部節點間的阻抗。各類節點間的阻抗計算結果如圖13～圖15所示。

通過對比不同類型節點間阻抗計算結果表明，距離相當的2個節點間阻抗值，當節點均處于邊界時節點間的阻抗值最大，節點均在內部時節點間的阻抗值最小。

6 結 論

通過對復合材料飛機接地回流網絡在不同參數、結構情況下阻抗值的對比分析，以及阻抗值的影響因素分析，得到如下主要結論：

1）搭接復合材料蒙皮會在一定程度上減小接地回流網絡節點間的阻抗，當復合材料蒙皮與金屬導軌接地回流網絡處于固定搭接方式下，這種效應隨著復合材料蒙皮的電導率的增大變得更加明顯。因此，電導率更大的復合材料，對于復合材料飛機接地系統的安全性和經濟性更加有利。

2）在金屬導軌截面積不變的情況下，截面形狀對金屬接地回流網絡阻抗的影響較大。計算結果表明，截面為工字形的金屬導軌阻抗值比同等截面積的正方形導軌小。

3）在滿足安裝及工作位置的前提下，將相關電氣設備的接地點選在內部節點所處的位置上，有利于減小接地點間的阻抗。

致謝感謝航空機電系統測試與故障診斷實驗室各位老師及同學在本文理論探討、實驗仿真及寫作過程中提出的寶貴建議和提供的幫助。