結合新型邊界擴展函數的水平集醫學圖像分割方法
朱家明,許 諾,張倚天,包 清,杭 俊
(揚州大學 信息工程學院,江蘇 揚州 225127)
0 引言
隨著科技的發展,很多醫生把醫學影像作為疾病診斷的重要依據之一。由于核磁共振成像(MRI)圖像具有對含水分的軟組織較為敏感的特性,經常用于對腦部組織進行解剖結構的分析與檢測[1]。但是MRI圖像的成像也有缺點,例如由于受到設備、環境和不均勻的射頻信號影響,圖像大多存在噪聲和灰度不均的問題[2]。
在醫學圖像處理領域,圖像分割是一個重要的技術[3],其任務是從圖像中提取有診斷價值的目標,是用于醫生臨床診斷的計算機輔助系統的重要組成部分。對于圖像分割,各國學者提出了多種方法,例如:閾值法、模式識別法、區域生長法、神經網絡法、小波變換法、模糊分割法、水平集方法[4]以及遺傳算法等。其中水平集方法是曲線演化問題的一種有效的求解方法[5-7],其最初由Osher和Sethian[8]提出,用于分析火苗的外形變化過程。在1989年,Mumford和Shah[9]提出了M-S模型。Chan[10]于2001年提出了單水平集CV模型,Vese[11]于2002年提出了多水平集CV模型,Li和Xu[12]于2010年提出了距離正則化水平集模型。為了解決MRI圖像的分割問題,本文提出了一種結合閾值法預分割的水平集分割方法。考慮到MRI圖像具有的高斯噪聲,先對其作低頻濾波處理。理論分析和實驗結果都驗證了該方法的有效性。
1 頻域濾波去噪
1.1 高斯噪聲與頻域濾波
作為圖像分割的前提條件,要求對噪聲先作有效抑制。高斯噪聲是醫學圖像中廣泛存在的一種噪聲,通常是由于電子元件的敏感性以及各種外界的電磁干擾造成的。消除高斯噪聲常用的方法有空間濾波與頻域濾波。因為噪聲信號一般都是高頻信號,當采用低通濾波時,選擇合適的截止頻率就能夠濾除大部分噪聲,同時保留圖像的邊緣和細節。而采用低通濾波的前提就是先對圖像進行傅里葉變換,使之轉換成頻域模型;然后針對頻域模型設計低通濾波器進行濾波;最后對濾波后的頻域模型進行傅里葉反變換,得到去噪的圖像。
計算機處理的都是離散化的系統,一幅灰度圖像可以表示為二維的離散函數,離散函數的二維傅里葉變換與傅里葉反變換公式分別為:
(1)
(2)
1.2 低通濾波
低通濾波方法有巴特沃斯濾波、切比雪夫濾波以及理想低通濾波等。其中理想低通濾波器屬于假想的低通濾波器,對于高頻(即高于截止頻率)信號完全截止,而對于低頻信號完全無失真傳輸。由于理想低通濾波去噪的效果要優于其他低通濾波,因此本文采用理想低通濾波去除噪聲,如圖1所示。

(a) FFT頻譜

(b) FFT頻譜

(c) ButterworthLPF頻譜

(d) 理想LPF頻譜
(e) 原始圖像
(f) 噪聲圖像

(g) ButterworthLPF圖像
(h) 理想LPF圖像
2 改進的水平集分割方法
2.1 閾值法的預分割
用閾值法先預分割,即設定水平集函數初值。水平集分割法步驟:先定一個初值(初始輪廓),再按照演化方程進行演化,即不斷更新水平集函數取值。相應改變了零水平集的輪廓曲線,完成了圖像分割。當達到設定標準,就停止演化并輸出結果。因為水平集的初值會對分割結果有一定的影響,所以選取合適的初值是有必要的。本文采用閾值法預分割(定水平集初值),用整幅圖像灰度區間的黃金分割數作為閾值,即取權值α=0.382。閾值的計算公式如下:
Ith=Ilow+0.382(Ihigh-Ilow),
(3)
式中,Ith為閾值,Ilow為整幅圖像的灰度值的下限,Ihigh為灰度值的上限。其中默認目標灰度值比背景灰度值小,反之如果目標灰度值比背景灰度值大,則取α=0.618,計算公式如下:
Ith=Ilow+0.618(Ihigh-Ilow)。
(4)
閾值法確定的初始輪廓圖如圖2所示。
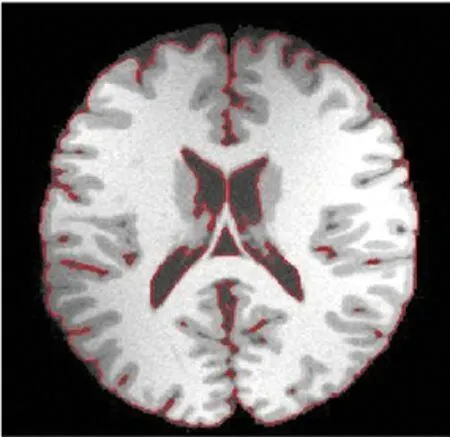
(a) α=0.382
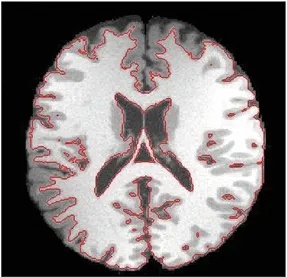
(b) α=0.618
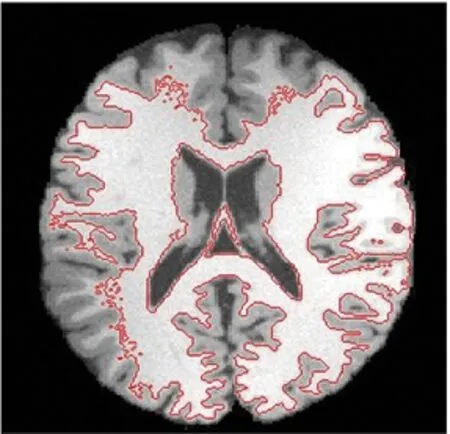
(c) α=0.85
2.2 水平集模型描述
水平集方法是依據水平集函數φ的取值將圖像劃分為目標和背景兩相。水平集函數定義為符號距離函數。即圖上一點(x,y)與目標輪廓曲線C的距離。表達式如下:
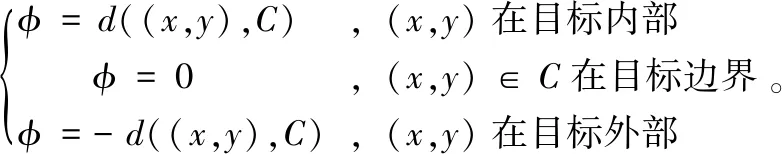
(5)
由式(5)可見,水平集函數取值為零的點的集合(零水平集)即為目標的邊緣輪廓。水平集函數原理如圖3所示,從圖中可見水平集函數φ將整個圖像分割成互不重合的兩個部分。
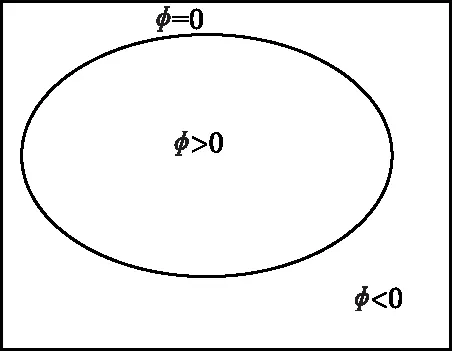
圖3 水平集區域劃分圖Fig.3 Level set area division diagram
水平集模型主要包括兩大類模型:一類是基于邊緣信息的模型,如Snake模型;另一類是基于區域信息的模型,如M-S模型、C-V模型和變分水平集等。本文考慮結合邊緣信息和區域信息的模型。
2.3 邊界擴展函數
本文設計一種新型的邊界擴展函數,并將它結合到傳統的能量函數中,用于解決目標邊界劃分細節不準確的問題。基本設想如下:在目標輪廓線附近,當目標外部灰度接近目標內部的灰度時,就使得目標輪廓線擴張,把外面這部分包含到目標內部來。該邊界擴展函數設計如下:
(1-H(φ))dxdy,
(6)
式中,u(x,y)表示目標外部某一點的灰度,cδ表示該點附近的目標局部的平均灰度。
。
(7)
水平集函數φ的演化方程為:
(8)
2.4 能量函數與演化方程
主動輪廓模型的能量泛函定義為:
E(C)=∮Ωg(|?I(C(s))|)ds。
(9)
對式(9)引入Hesviside函數,結合格林公式,可改寫成:
Es(φ)=?Ωg(x,y)‖?H(φ)‖dxdy,
(10)
式中,φ表示水平集函數,g(x,y)為反映邊緣特征的函數,表達式如下:
p≥1。
(11)
曲線演化的目標是使能量泛函取得極小值。根據E-L方程和梯度下降法,解得演化方程為:
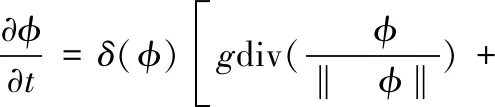
(12)
C-V模型的能量泛函定義為:
E(c)=μ·length(C)+
λ1?Ω1(u(x,y)-c1)2dxdy+
λ2?Ω2(u(x,y)-c2)2dxdy,
(13)
式中,μ、λ1、λ2為正的常數,u(x,y)為圖像灰度函數。引入Hesviside函數后能量泛函為:
Ecv(φ)=μ?Ω‖?H(φ)‖dxdy+
λ1?ΩH(φ)(u(x,y)-c1)2dxdy+
λ2?Ω(1-H(φ))(u(x,y)-c2)2dxdy,
(14)
對應的演化方程為:
(15)
將泛函(14)對c1求偏導,令它等于0可求得c1。同理可求得c2,公式如下:
(16)
(17)
為了避免在演化過程中出現重新初始化的問題[15],在能量泛函(14)中增加懲罰項Ep(φ):
(18)
式中,ν為正的常數。綜上所述,能量函數定義為:
E(φ)=Ecv(φ)+Ep(φ)+Es(φ)+Eex(φ)=
μ?Ω‖?H(φ)‖dxdy+
λ1?ΩH(φ)(u(x,y)-c1)2dxdy+
λ2?Ω(1-H(φ))(u(x,y)-c2)2dxdy+

α?Ωg(x,y)‖?H(φ)‖dxdy+
。(19)
對應的演化方程為:
λ1(u-c1)2+λ2(u-c2)2+
(20)
式中,Δ表示拉普拉斯算子。
2.5 算法流程
算法流程為:① 加載原始圖像;② 用理想低頻濾波消除噪聲;③ 用閾值法進行預分割;④ 用水平集方法進行圖像分割;⑤ 輸出分割結果圖。
3 實驗結果與分析
實驗環境:硬件Huawei MateBook X Pro,RAM 8.0 G,CPU CORE i7-8550U 1.80 GHz; 軟件 Windows10中文版,MATLAB 7.0。選取一幅腦部MRI圖像進行去噪預處理,迭代次數為200次。參數設置為:α=3,μ=5,v=1.5,λ1=λ1=10-6,采樣時間間隔Δt=0.02。分別采用C-V算法和本文算法來分割去噪后的MRI圖像,分割結果如圖4所示。由圖可見,本文的算法分割的效果優于C-V算法。
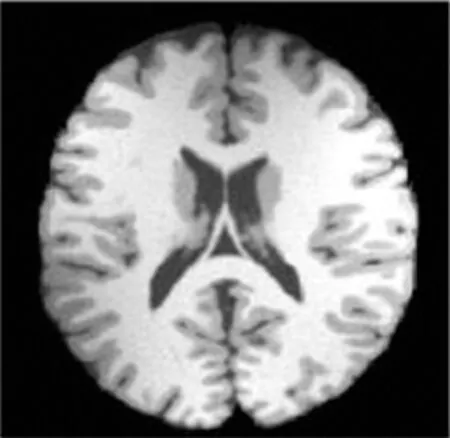
(a) 原始圖像

(b) C-V算法
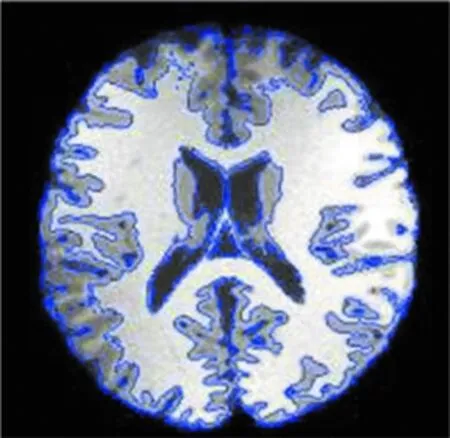
(c) LSE算法
采用Jaccard Similarity(JS)指標來對分割結果進行評價[13]:
(21)
指標值越大代表分割效果越好,表1為C-V算法與本文算法的JS指標,數據顯示本文算法的分割效果優于C-V算法。
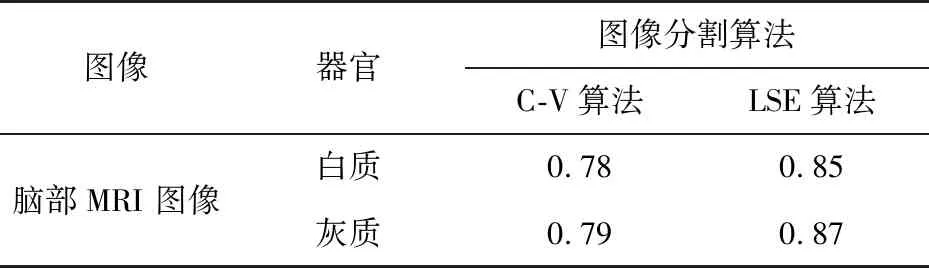
表1 兩種算法的JS指標
4 結束語
本文提出一種結合新型邊界擴展函數的水平集圖像分割方法。首先用理想低頻濾波對圖像進行去噪處理,同時兼顧去噪效果和保留細節兩個目標,然后用閾值法確定目標的初始輪廓。提出新型邊界擴展函數,并整合到能量函數中。在其中增加懲罰項,避免了在演化過程中的重新初始化。實驗結果表明,該方法能夠準確地分割含有高斯噪聲的灰度不均的MRI圖像。

