正則化與ELM結合用于光伏發電功率預測

李正剛， 王智方， 鐘建偉， 張欽惠， 程明亮

(1.國網湖北省電力有限公司巴東縣供電公司,湖北 巴東 445000；2.湖北民族大學 信息工程學院,湖北 恩施 445000)

0 引 言

傳統化石能源在枯竭，可再生能源進入人們的視線[1]。太陽能是較好的替代能源[2]，人們越來越關注光伏發電預測[3]。光伏發電受制于太陽輻射和天氣因素[4],影響了電網的運行和調度[5]。

ELM在回歸分析、分類和預測領域都有極快的學習速度[6]。該算法還可以降低陷入局部最優的可能性[7]。正則化通過約束最小化經驗誤差函數來解決逆問題的不適定性，改善用于求解數據的精度[8]。

本文提出一種使用正則化方法優化ELM數據精度的預測方法。引入正則化項改進ELM的泛化能力，避免過擬合，改善用于求解的數據的精度，提高預測的精度。采用DKA太陽能中心的實際數據以驗證預測方法提高光伏發電預測精度的能力。

1 正則化理論

正則化理論(regularization theory)在數值分析分析領域應用較多，穩定有效是該理論的特點。正則化方法包括截斷奇異值分解(truncated singular value decomposition，TSVD)方法和其他一些改進的算法。

TSVD方法以奇異值展開為基礎，k核的平均收斂展開式為:

(1)

式中:ui和vi為正交函數序列，且所有的μi≥0。其解為：

(2)

式中：(ui,g)為內積。只有當系數(ui,g)比ui更快地衰減到零時，解f才能存在。

(3)

這就是著名的皮卡德條件。

2 ELM算法

極限學習機(ELM)算法的目的就是解決基于梯度算法收斂慢和存在局部極小值等相關的問題，該算法是一種單隱層前饋神經網絡學習算法。ELM的學習速度非常快。在大多數情況下，ELM在泛化能力方面優于基于梯度的學習。

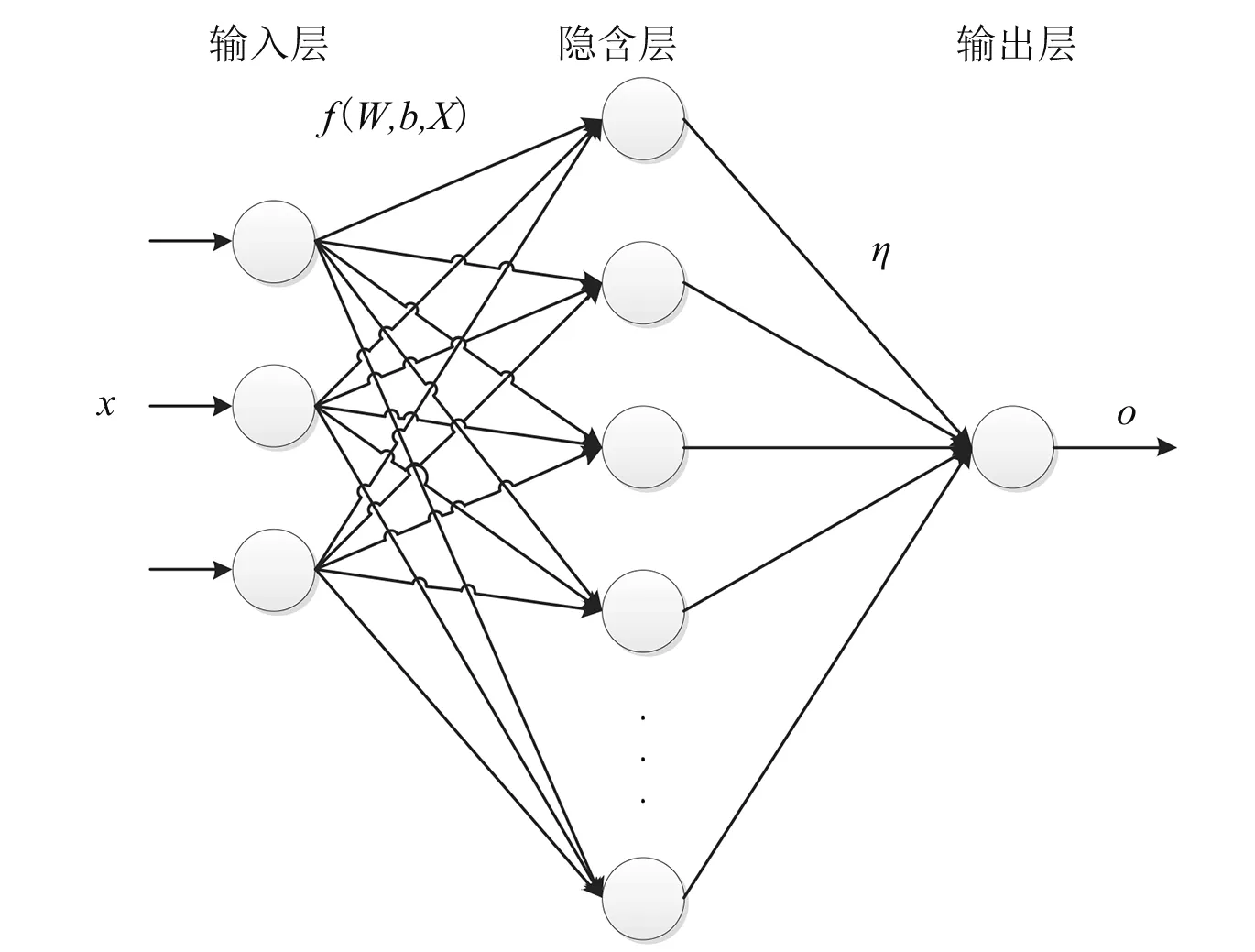
圖1 經典ELM結構圖

(4)

式中：Wj為第j個隱含層神經元與輸入向量Xi間的權值向量；bj為第j個隱含層神經元的閾值；ηj為第j個隱含層神經元與輸出層節點間的權值；oi為第i個樣本的輸出。

3 正則化優化ELM算法的光伏功率預測

3.1 預測流程

如圖2所示，首先需要整理輻照量等特征向量的時間序列，對整理出來的數據進行歸一化處理，處理后的數據劃分為訓練集和測試集。訓練集決定最優的隱含層節點數、確定正則化參數并進行正則化過程。然后，解出對應的η。最后，把得到的參數使用到測試集中進行預測。

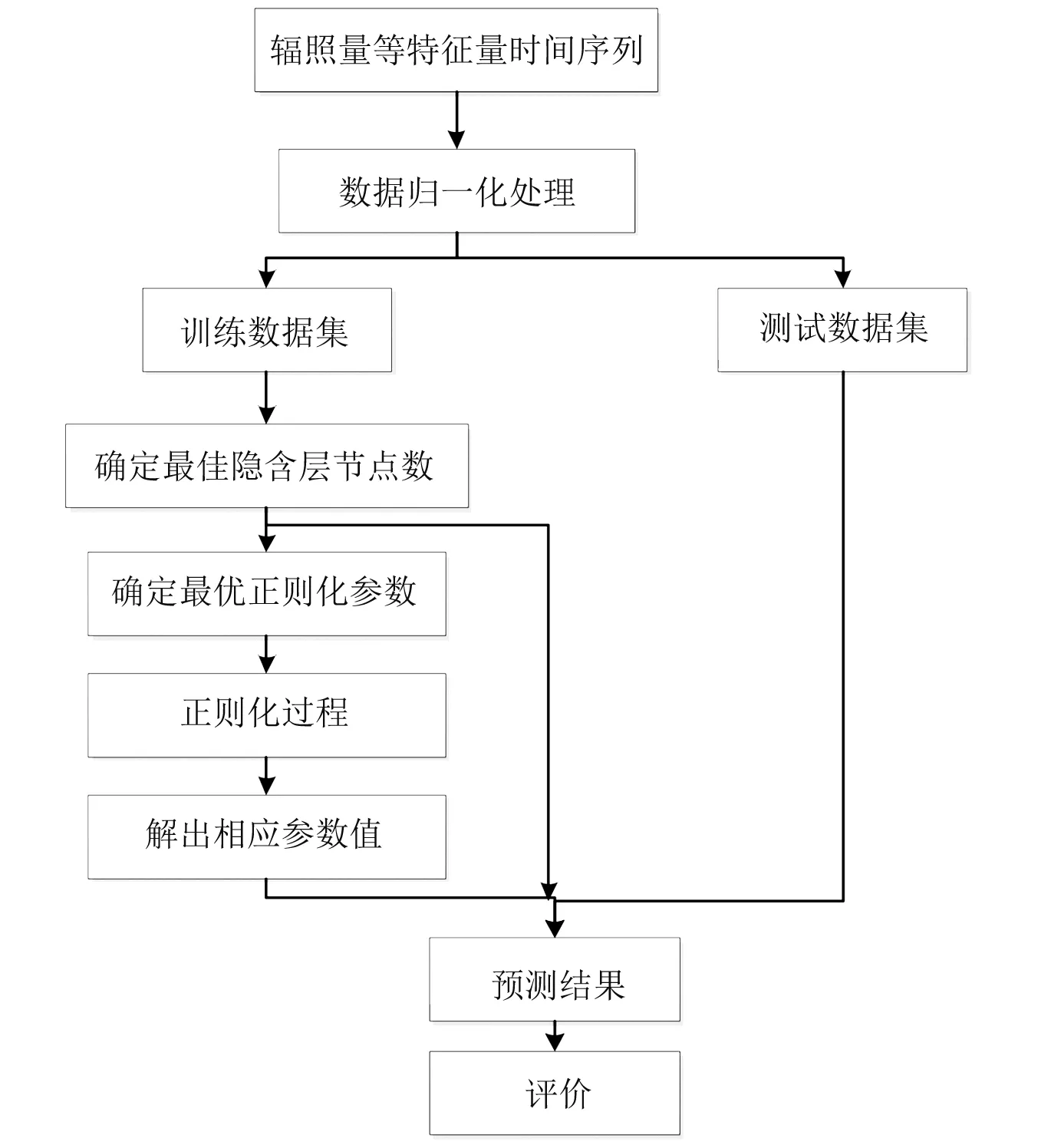
圖2 正則化優化ELM算法預測流程圖

具體為：①由于天氣因素與設備因素均對預測結果產生影響，選定歷史發電數據量、總輻射量、直射輻射、散射輻射、環境溫度、風向(力)、氣壓、相對濕度、組件的溫度和組件的電流電壓等參數為特征向量。整理輻照量等特征向量的時間序列，對整理出來的數據進行歸一化處理，把處理過的數據分成訓練集和測試集。②先通過訓練集決定最優的隱含層節點數，然后確定最優正則化參數，再進行正則化過程，最后將得到的參數使用到測試集，進行預測。③通過相關誤差系數評價預測結果的精度。

3.2 誤差評價

本文在評價仿真預測結果精度時使用均方誤差MSE與決定系數R2。

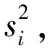
(5)

決定系數，也稱為判定系數或者是擬合優度。當R2趨近于1時，說明相關方程越值得參考；相反，趨近于0時，說明相關的方程沒有參考的意義。

在多元回歸分析中，決定系數是通徑系數的平方，其表達式為：

(6)

式中：SST為總平方和；SSR為回歸平方和；SSE為殘差平方和。SST=SSR+SSE，擬合優度越大，自變量對因變量的解釋程度越高，觀察點在回歸直線附近越密集。

決定系數:為0時，表示模型效果跟瞎猜差不多；為1時，表示模型擬合度較好；在0～1時，表示模型的好壞(針對同一批數據)；小于0時，說明數據不存在線性關系。

4 仿真分析與結果

本文數據使用的是澳大利亞DKA太陽能中心提供的某地區光伏發電站2018年1月1日至2018年12月31日的歷史數據。選取的時間間隔為5 min，選取的數據共105 230組。由于光伏發電受自然因素影響較大，尤其是輻射量、溫度、風向、風力和相對濕度。因此，綜合考慮，每組數據選定的特征向量包括：歷史發電數據量、總輻射量、直射輻射、散射輻射、環境溫度、風向(力)、氣壓、相對濕度、組件的溫度和組件的電流電壓等參數。訓練集數據為105 000組，測試集數據為230組。利用MATLAB仿真軟件進行了光伏發電功率值的仿真預測和相應的評價值計算。

4.1 仿真結果分析

圖3為正則化優化ELM預測波形與真實波形圖,圖4為ELM預測波形與真實波形圖。圖3、圖4中橫坐標為測試集樣本編號，縱坐標為光伏發電功率。通過計算得到，正則化優化ELM預測波形預測結果均方誤差為0.002 58，決定系數為0.999 97。ELM預測波形預測結果均方誤差為0.011 18，決定系數為0.999 89。

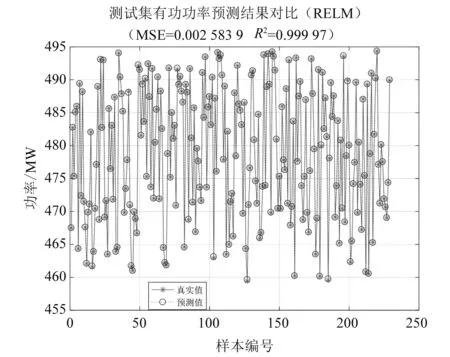
圖3 正則化優化ELM預測波形與真實波形

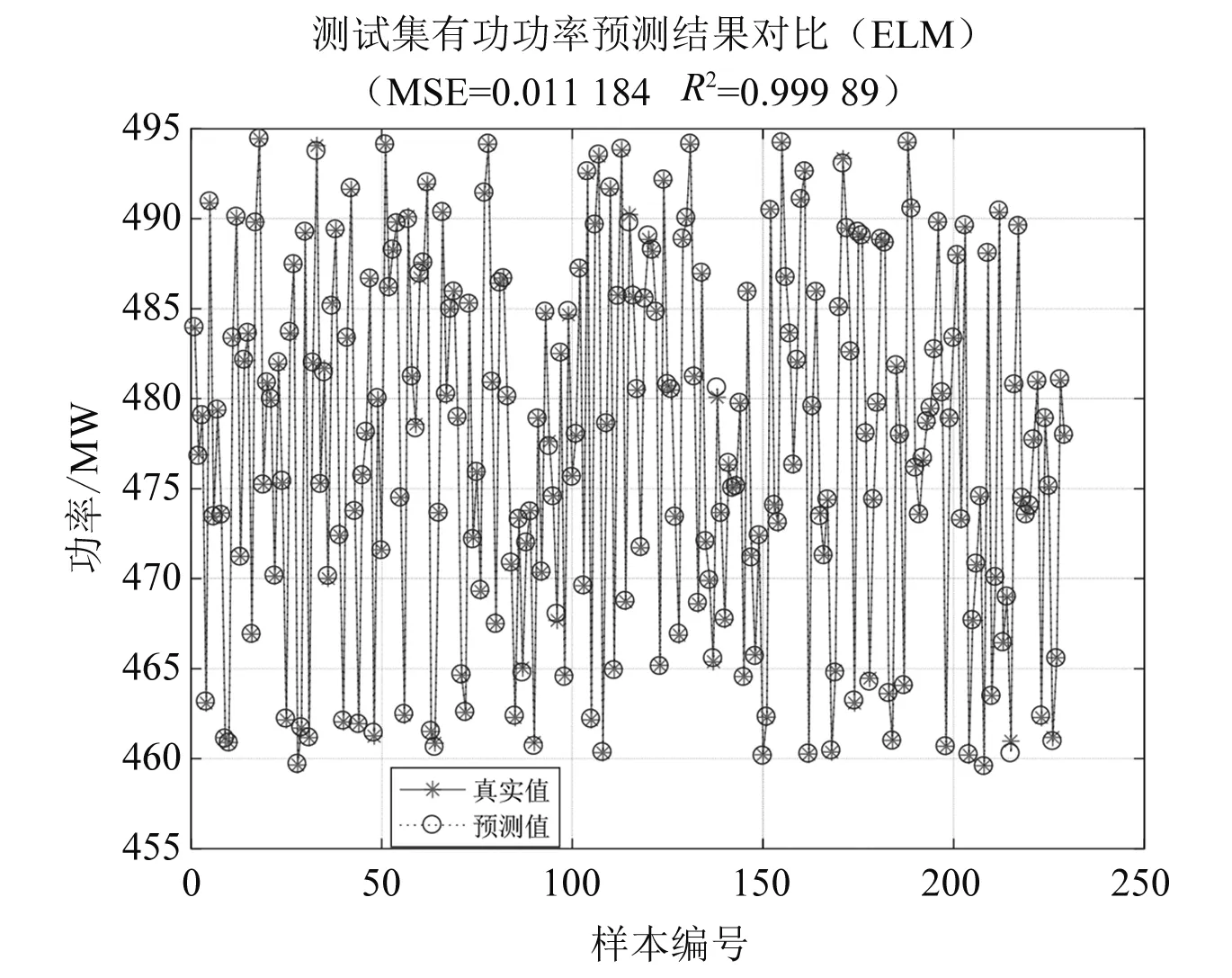
圖4 ELM預測波形與真實波形

4.2 仿真對比

對比兩種方法預測結果的評價值可知，優化前的預測結果中，均方誤差為0.011 18，決定系數為0.999 89，優化后的預測結果中，均方誤差為0.002 58，決定系數為0.999 97。均方誤差降低了0.008 6，決定系數提高了0.000 05。由仿真波形圖可知，預測的精度得到改善。

5 結束語

極限學習機(ELM)是一種前饋神經網絡，克服了傳統神經網絡學習算法(如BP算法)極易陷入局部最優、學習速度慢的缺點。利用正則項化處理數據的特點，對ELM進行優化，最終解不會過擬合，可以提高預測的精度。本文使用實際的歷史發電數據以及歷史天氣數據，以正則化優化ELM算法進行光伏發電功率預測。利用MATLAB仿真軟件進行了光伏發電功率值的仿真預測和相應的評價值計算。最后，通過仿真波形圖驗證，該方法可以改善預測的精度。