基于多機載預警雷達的機動目標融合跟蹤方法

戴 瑜，龍文佳

（湖北大學知行學院，武漢 430019）

0 引言

多機載預警雷達通過協同探測，可以實現對機動目標的精確跟蹤，獲得目標的狀態及屬性信息，形成完整的戰場態勢，奪取現代戰爭的制信息權［1］。

機動目標的跟蹤是多機載預警雷達數據融合研究中的一個難點，當前，對機動目標的跟蹤采用的主要方法為基于卡爾曼濾波的BLUE 算法和IMMPDAwoOoSM 算法［2-6］。然而，由于目標運動狀態和雜波環境的復雜性，使得傳統的卡爾曼濾波本身不足以完全解決該問題。為此，本文基于量測噪聲協方差估計設計了一種優化了的卡爾曼濾波器［7-8］，引入了協方差交集的概念，提出了一種針對多機載預警雷達數據融合中機動目標跟蹤的新方法。相比現有的方法，該方法具有更高的跟蹤精度。

1 基于量測噪聲協方差估計的優化卡爾曼濾波器設計

假設在一般情況下，對于以恒定速度直線運動的目標而言，目標速度的加速度符合高斯白噪聲特性，則可以對卡爾曼濾波器進行以下優化和調整［9-10］。目標的狀態方程模型可以表示為

其對應的噪聲協方差表示為

該協方差矩陣通常表現為高斯白噪聲協方差矩陣，現在考慮狀態矩陣的構建

從式（6）可以看出，加速度矢量被認為是一種狀態噪聲，可以通過Fk矩陣進行狀態估算。于是修改的協方差表示為

以上優化過程，僅對目標以恒定速度直線運動時的優化有效。如果目標方向發生機動或改變，則以上估計器的過程噪聲將增加，而且這種噪聲也不再是高斯白噪聲，但可以合理地將其視為測量噪聲。

實際測量向量與估計向量之間的誤差為

基于式（10），同時考慮引入的測量噪聲，則上式可表示為

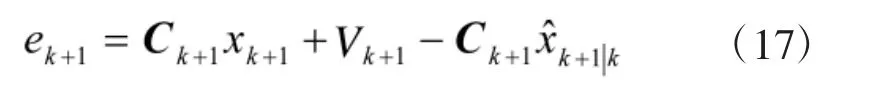
進而，由式（17）可以得到測量噪聲Vk+1的表達式

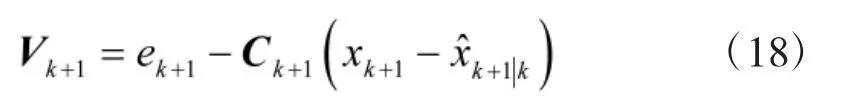
則該測量噪聲向量的協方差及其協方差矩陣Rk+1為

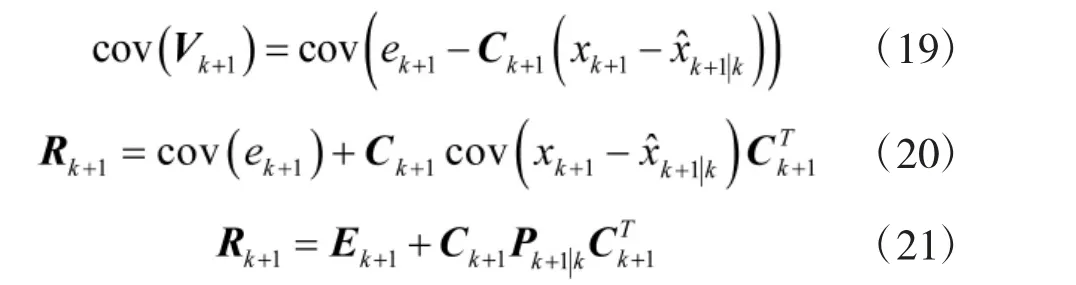
測量誤差協方差的估算可以由滑動平均濾波器實現

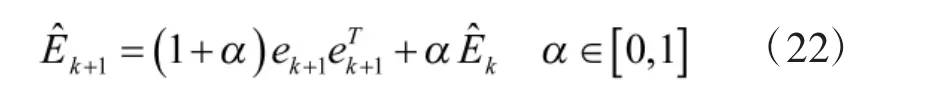
該濾波器具有統一的穩態增益，并且α 可以用滑動平均濾波器的點數n 表示為

可以重新排列，由α 找到所需的滑動平均濾波器的點數n 如下

其中，α 的值可以通過模糊邏輯方法給出最佳估計。

在檢測概率較高的情況下，由式（16）可知，強機動目標會使真實測量值與測量的預測值間的偏差變大，使式（22）所表征的不確定性增大，進而進一步使式（21）所表征的測量方差增大。根據式（13）可得，測量不確定性的增加使得濾波增益減小，從而在狀態更新中對濾波值的計算更依賴于狀態的預測，而不是最新的測量信息，此時勻速直線運動模型的設定便限制了對機動目標的跟蹤性能。但是，在本文方法中，采用了滑動平均濾波對信息協方差進行估計，通過濾波系數的自適應更新，能夠有效調整信息不確定性的大小，對機動目標給出更大的濾波增益，以此提高對機動目標的跟蹤新能。

2 滑動平均濾波器參數的估計

由式（24）可知，估計出α 的值就能確定合適的滑動平均濾波器的采樣點數n。本文采用Bellman和Zadeh 提出的模糊邏輯理論［11］，用于優化測量協方差的Fresenius 范數方差，這種方法確保了模糊目標函數和模糊約束都有同樣的約束條件。具體約束條件如下：

1）當目標發生轉向機動，噪聲是非高斯，需要最小化Frobenius 測量協方差。

2）重構前提是系統中噪聲通過小的加速條件產生。

對于測量噪聲協方差矩陣的估計Frobenius 范數的平均值，可表示如下

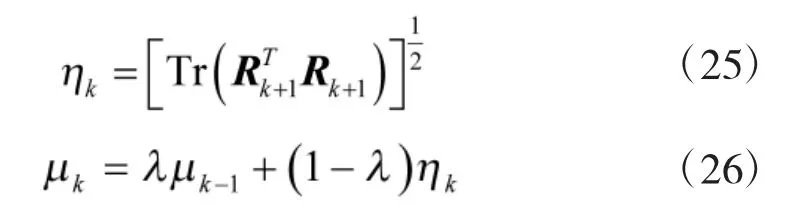
則模糊隸屬方程和精確遞歸方差由下式給出

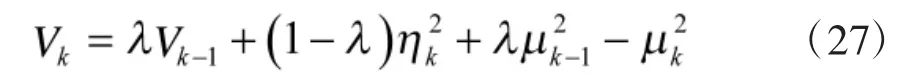
上式可以近似為

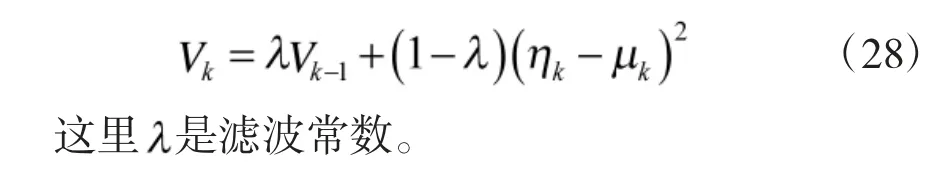
在每次迭代時，將對比當次Vk與前面最大Vmax值，如果Vk＞Vmax，則Vk用代替Vmax。然后模糊隸屬函數橫坐標刻度確定為

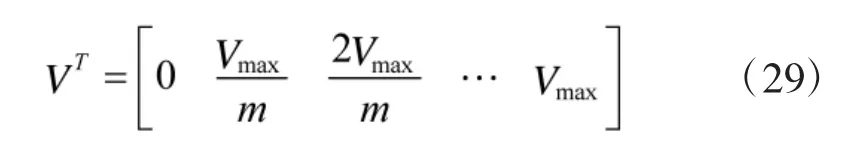
該集合將方差模糊化為隸屬度。這實際上是將模糊化與基于規則的模糊推理相結合的模糊推理。這樣，通過去模糊化處理，給出了優化的濾波系數

圖1 模糊推理隸屬函數值

圖1 給出模糊推理隸屬函數值的示意圖。這種簡單的線性組合產生可接受的性能，但需要進一步研究來調整α 和隸屬函數橫坐標。

3 多機載預警雷達數據融合

多機載預警雷達協同探測時，需要將多組跟蹤信息融合在一起，以產生一致的態勢感知，即協方差交集［12］。協方差交集采用在信息空間中表示的平均和協方差估計的凸組合［13-15］。在這種意義上，這種凸組合是一致的，即所得到的協方差超橢圓體包含在每單個估計器的所有協方差超橢圓體的外界。

下面給出了基于兩傳感器信息交集的一致協方差和平均估計值μ∈［0，1］

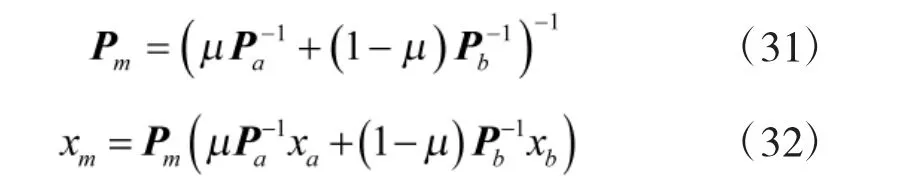
對于n 部傳感器交集，可以應用一般均勻加權方案，隨著更多信息可用及接收到的數據可靠性變化而可以相應變化。下面給出具體實現方法：

4 仿真分析

為了驗證本文方法的有效性，首先設置了具有一個目標和兩個機載預警雷達傳感器平臺的仿真環境，如圖2 所示。兩個雷達傳感器的飛行平臺分別在5 000 m 的高度以150 m/s 和100 m/s 的速度巡航。運動目標在1 000 m 高度，以200 m/s 的速度巡航。

仿真中，高斯白噪聲被傳入位置和角度零均值和方差測量分別為30 m/s2和0.1 mrd。當采納簡單卡爾曼濾波方法，這些噪聲的傳入會導致在非線性目標估計器中產生相當大的誤差。

圖2 機載預警雷達和目標的幾何位置關系圖

圖3（a）給出了目標所在區域內的飛行路線，為橢圓形跑道，圖3（b）給出了非直線段的實際航行的速度值。圖4 給出了基于常規卡爾曼濾波的目標航跡融合和跟蹤結果，可以看出，融合的位置和速度值誤差較大，融合航跡起伏較大，不平穩。圖5 給出了基于本文算法的融合結果，可以看出目標的位置和速度估算誤差小，速度誤差減小了一個數量級，使其成為位置預測的可用度量，融合航跡平滑且接近真實航跡。該算法能夠優化模糊邏輯反饋控制滑動平均濾波恒定遞歸地測量方差，并允許系統不斷適應任何性質的噪聲改變，重新計算狀態協方差矩陣和估計測量噪聲協方差矩陣。

圖3 目標的實際位置和速度

圖4 基于常規卡爾曼濾波的目標航跡跟蹤結果

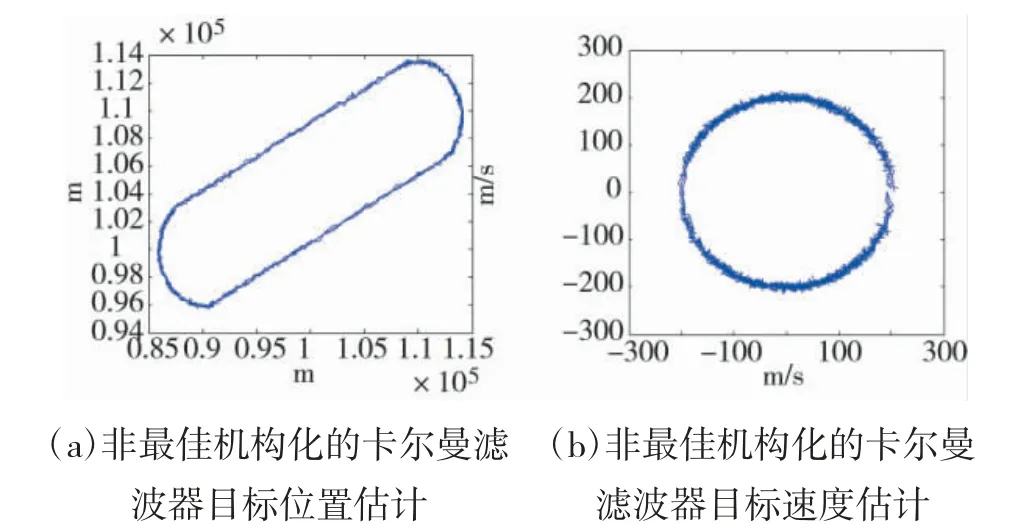
圖5 基于本文算法的目標航跡跟蹤結果

假設目標機動飛行，目標的起始位置為（120.8°E，40.1°N），飛行過程中高度始終為6 000 m，航線上有兩個機動拐彎點，分別是（119.9°E，39.9°N）和（120.3°E，40.2°N），拐彎點之間目標直線飛行，目標的機動轉彎采用常速率轉彎模型進行描述。

仿真中，設置兩部預警機，預警機航線均為直線飛行，兩者的速度均為250 m/s。其中，第1 部預警機在（118.7°E，40.2°N）和（120.2°E，40.2°N）之間勻速飛行，高度6 040 m；預警機2 在（118.7°E，39.8°N）和（120.2°E，39.8°N）之間飛行，高度6 000 m。

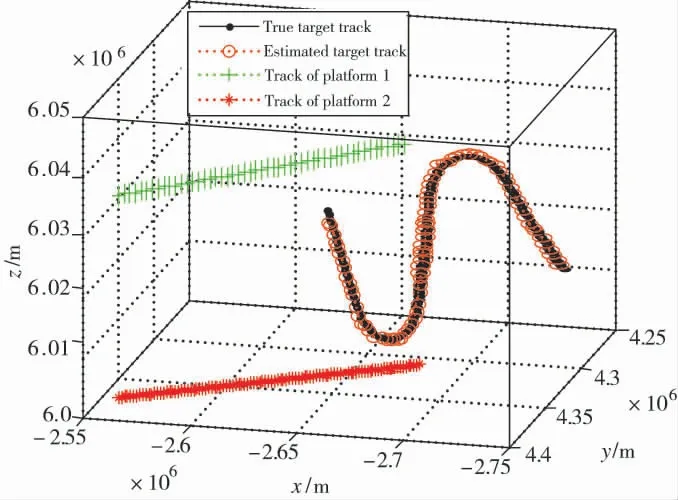
圖6 基于本文算法的融合仿真結果

圖6 給出了基于本文提出算法的目標跟蹤結果。從圖中可直觀看出，本文提出的算法成功穩定地跟蹤機動的運動目標。圖7 給出了300 次蒙特卡洛實驗的位置和速度均方根誤差（RMSE）性能比較結果，其中，包含BLUE 算法、IMMPDAwoOoSM 算法（“亂序”目標中未利用OoSM 測量的IMMPDA 算法）［3］，結果表明本文算法的誤差性能是最佳的。需要指出的是，每次仿真中均對目標和機載雷達的初始位置、初始速度加入一定的隨機擾動以模擬實際場景中的不確定性，再加上起始時刻濾波器尚未收斂，濾波誤差相對較大，因此，造成起始誤差的不同。

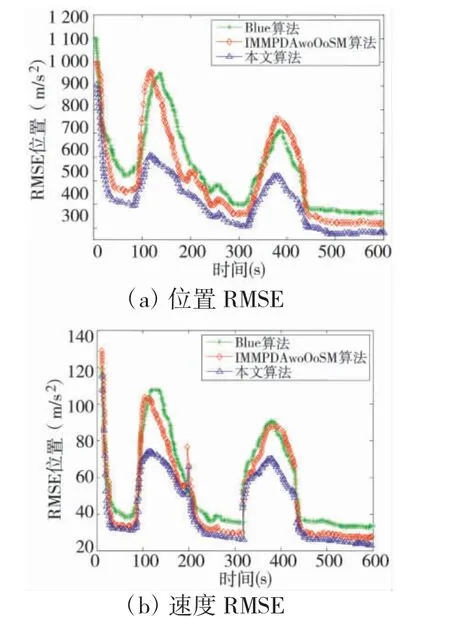
圖7 跟蹤性能比較

5 結論

針對多機載預警雷達信息融合中的機動目標跟蹤問題，本文從轉換量測Kalman 濾波角度，提出了一種多機載預警雷達平臺跟蹤機動目標的新方法。該方法通過噪聲源進行重組，簡化噪聲協方差模型狀態，從優化單系數滑動平均濾波器來估算測量噪聲協方差，通過基于優化模糊邏輯，使利用協方差矩陣估算測量的羅伯尼范數方差最小化，仿真分析表明，該方法能夠較好解決多機載預警雷達數據融合中的機動目標跟蹤問題。