兩種鋼結(jié)構(gòu)電梯井道抗震性能對比分析

曹 靖

(安徽富煌鋼構(gòu)股份有限公司，安徽 巢湖 238076)

1 概述

近些年來，社會發(fā)展迅速，人民生活的水準也隨之提高。在建筑行業(yè)發(fā)展比較落后的初期，一些修建較早的老舊住宅和小區(qū)僅有步行樓梯，對于樓上尤其是3層以上居民的生活來說，不是特別方便，再者給一部分老人的上下樓帶來很多困擾。因此，為這些僅有步行樓梯的住宅加裝一部電梯變得尤為重要。1999年，在《住宅建筑設(shè)計規(guī)范》中指出，“七層(含七層)以上應(yīng)設(shè)電梯”。2019年，為了加深在僅有建筑的外部增加電梯的工作，改善老舊小區(qū)的上下樓條件，更好的提高人們的生活水準，安徽省住房和城鄉(xiāng)建設(shè)廳、安徽省市場監(jiān)管局等聯(lián)合引發(fā)了《關(guān)于城市既有住宅增設(shè)電梯工作的指導(dǎo)意見》的通知，明確在不破壞原來的建筑物的結(jié)構(gòu)原則上，可以在主體外部加裝電梯。

加裝電梯的結(jié)構(gòu)形式主要有兩種：一種是鋼結(jié)構(gòu)，另一種是鋼筋混凝土。但鋼結(jié)構(gòu)的自重較輕，安裝也較為方便。段柏安[1-3]通過對三種結(jié)構(gòu)形式的建筑進行了模態(tài)分析等，得到了鋼結(jié)構(gòu)住宅的經(jīng)濟型和抗震特點。張鵬飛[4,5]采用midas/gen對某辦公樓實行了模態(tài)分析，得到其性能。林宏偉[6]以6層辦公樓研究了建筑加裝電梯后相互作用的影響，探討了兩者間的相互規(guī)律。唐柏鑒[7]用SAP2000對三層鋼框架用底部剪力法與手算進行分析，對結(jié)構(gòu)進行了優(yōu)化。本文通過midas/gen對直梁和弧形梁鋼框架電梯井道兩種形式的抗震特點進行了分析，最終得到了兩種形式的電梯井道的抗震特點并進行比較。

2 建立鋼結(jié)構(gòu)電梯井空間計算模型

本文使用midas/gen對該兩種鋼框架電梯井道結(jié)構(gòu)進行模擬分析。選取鋼材料為Q345，彈性模量為2.06×1011Pa，密度為7.85 g/cm3，泊松比0.3。直梁電梯井道結(jié)構(gòu)主肢為4根200 mm×200 mm×8 mm的方管，四周橫梁采用HN250 mm×125 mm×6 mm×9 mm的H型鋼，平面示意圖如圖1所示；弧形梁主肢為4根150 mm×150 mm×5 mm的方管，側(cè)面橫梁與弧形梁均采用120 mm×80 mm×4 mm的矩形鋼管，平面示意圖如圖2所示。

兩種鋼結(jié)構(gòu)電梯的安全等級為二級，重要性指數(shù)是1.0，重現(xiàn)期50年，使用荷載皆相同，如下，屋面恒載(不含自重)為0.7 kN/m2，活荷載為0.5 kN/m2，基本風壓0.40 kN/m2，基本雪壓0.60 kN/m2，地面粗糙度類別為B類，二類場地，抗震設(shè)防烈度為8度。

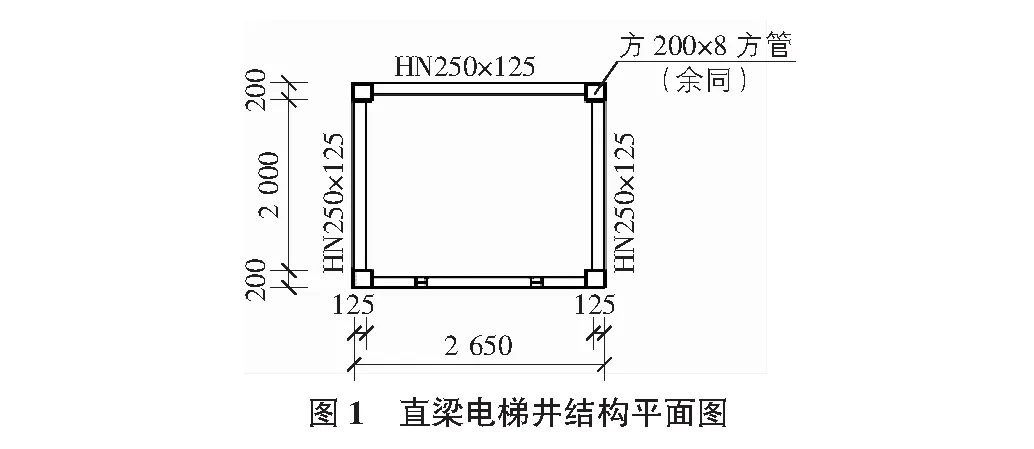
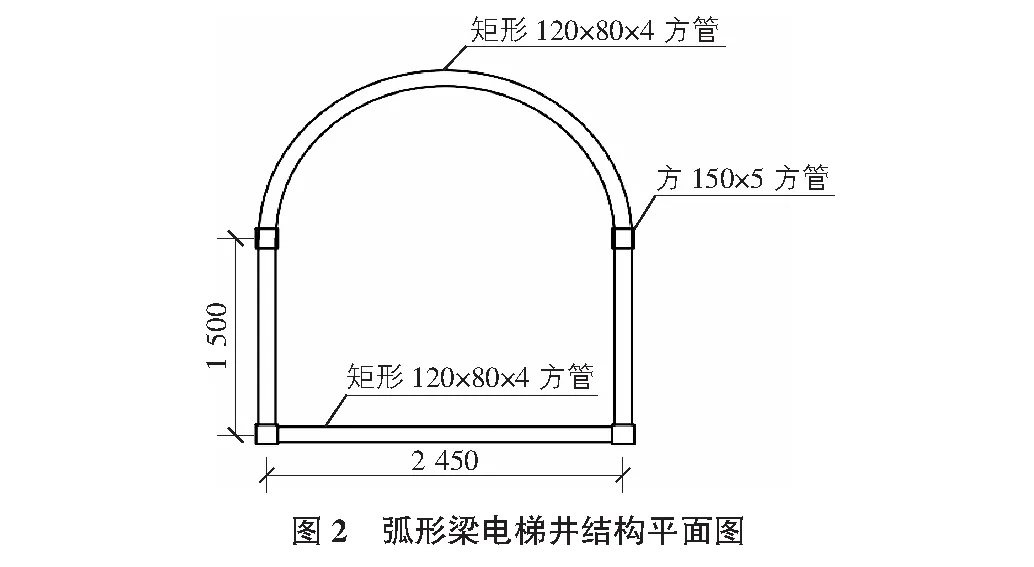
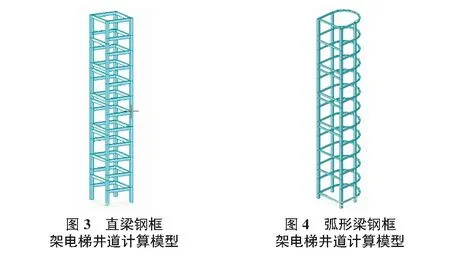
使用midas/gen有限元軟件對該兩種鋼框架電梯井道結(jié)構(gòu)進行建模，結(jié)構(gòu)所使用的梁柱皆為梁單元形式，梁柱之間的連接方式為剛性連接。得到直梁鋼框架電梯井道計算模型如圖3所示，弧形鋼框架電梯井道模型如圖4所示。

3 兩種電梯井結(jié)構(gòu)地震作用分析

在確定好此兩種電梯井的計算模型及具體信息后，對該結(jié)構(gòu)在地震作用下的抗震性能進行分析。本文根據(jù)選取相同的地理位置特征周期，抗震設(shè)防烈度，對這兩種鋼結(jié)構(gòu)電梯井道在X方向上和Y方向上的地震作用下的模態(tài)分析進行了研究，而后又在多遇地震Taft Lincoln School 69 Deg以及Taft Lincoln School 339 Deg下進行了時程分析。最終獲得了直梁和弧形梁電梯井道結(jié)構(gòu)的抗震特點與性能。

3.1 模態(tài)分析

模態(tài)分析是常用的研究結(jié)構(gòu)特性的方法之一，本文通過對該兩種鋼框架電梯井道進行模態(tài)分析，即得到這兩種電梯井道的自振頻率和振型等信息。結(jié)構(gòu)重量的計算方法為1.0恒載+0.5活載，將恒載與荷載轉(zhuǎn)化為結(jié)構(gòu)自重。最終確定這兩種結(jié)構(gòu)的特性如表1，表2所示。并選取兩種結(jié)構(gòu)前三階振型圖如圖5，圖6所示。

表1 直梁電梯井的振型參與質(zhì)量與周期 %

表2 自振周期

由表1可以看出，直梁鋼框架電梯井道質(zhì)量參與達到90%以上，弧形梁電梯井道質(zhì)量參與達到80%以上。此外，弧形梁電梯井道每一階自振周期均比直梁電梯井道的周期要長(見表2)。再根據(jù)兩者的前三階振型圖觀察了解到，第一階為結(jié)構(gòu)在X方向上的震動，第二階為結(jié)構(gòu)在Y方向上的震動，第三階為結(jié)構(gòu)的扭轉(zhuǎn)振型。根據(jù)相關(guān)規(guī)范，T3/T1=0.197/0.258=0.76(直梁鋼框架電梯井道的周期比)<0.85(規(guī)范規(guī)定限值)；T3/T1=0.305/0.568=0.54(弧形梁鋼框架電梯井道的周期比)<0.85(規(guī)范規(guī)定限值)，兩者均滿足要求。

3.2 時程分析

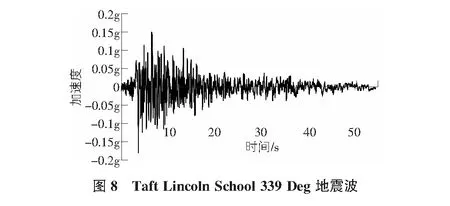
時程分析法是一種常見的研究結(jié)構(gòu)抗震的方法。現(xiàn)采用有限元軟件midas/gen對直梁和弧形梁鋼框架電梯井結(jié)構(gòu)進行時程分析。本文采用相同的場地類別，抗震設(shè)防烈度以及阻尼比等信息，后選取Taft Lincoln School 69 Deg地震波和Taft Lincoln School 339 Deg地震波對這兩種不同的鋼框架電梯井道結(jié)構(gòu)進行地震作用下的模擬分析下，從而得出兩種結(jié)構(gòu)的抗震特點。Taft Lincoln School 69 Deg地震波圖如圖7所示，Taft Lincoln School 339 Deg地震波如圖8所示。

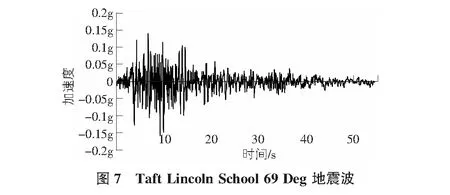
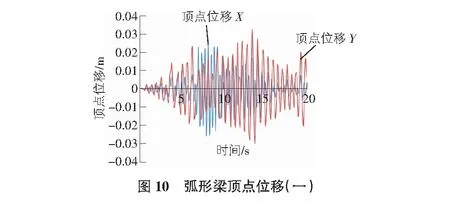
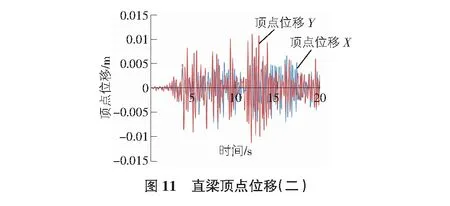
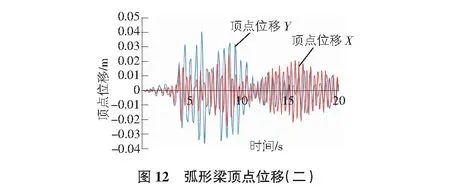
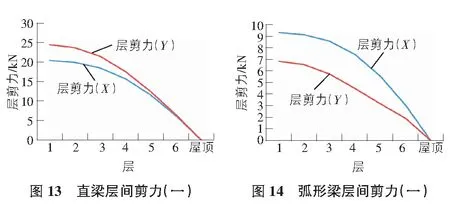
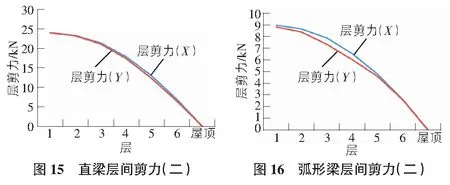
使用這兩條地震波分別對兩種鋼結(jié)構(gòu)形式進行X和Y方向上的地震作用模擬分析。最終獲得了兩種鋼框架電梯井道結(jié)構(gòu)在Taft Lincoln School 69 Deg地震波下的頂點位移如圖9，圖10所示；兩種鋼框架電梯井結(jié)構(gòu)在Taft Lincoln School 339 Deg地震波下的頂點位移圖如圖11，圖12所示。兩種電梯井道結(jié)構(gòu)在Taft Lincoln School 69 Deg地震波下的層間剪力如圖13，圖14所示，兩種電梯井道結(jié)構(gòu)在Taft Lincoln School 339 Deg地震波下的層間剪力如圖15，圖16所示。

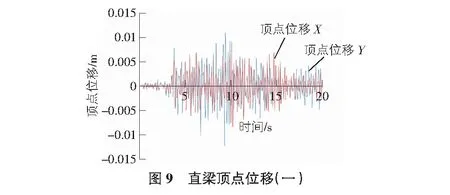
由圖9～圖12可知，在Taft Lincoln School 69 Deg地震波和Taft Lincoln School 339 Deg地震波作用下，兩種梁結(jié)構(gòu)形式的鋼框架電梯井道在X和Y方向上的頂點位移大小十分接近，此外，在Taft Lincoln School 69 Deg地震波作用下，直梁鋼框架電梯井道在X方向上頂點位移較大，而弧形梁鋼框架電梯井結(jié)構(gòu)形式在Y方向上的頂點位移較大。總體來說，在兩條地震波作用下，弧形梁在地震波作用下的頂點位移比直梁要長。再由圖13～圖16可以看出，兩種鋼框架電梯井結(jié)構(gòu)在地震波作用下的層剪力均在底層最大隨著樓層的增高逐漸遞減，此外，直梁的層剪力要比弧形梁的層剪力大。

4 分析與結(jié)論

本文在有限元軟件midas/gen中，對兩種常見的電梯結(jié)構(gòu)形式(直梁鋼框架電梯井道結(jié)構(gòu)和弧形鋼框架電梯井道結(jié)構(gòu))進行了模態(tài)分析與時程分析。在模態(tài)分析中可以了解到，弧形梁結(jié)構(gòu)形式電梯井道的自振周期要比直梁結(jié)構(gòu)形式的自振周期長一些，每階的自振周期都較為接近，二者的周期比都小于規(guī)范中規(guī)定的限值。根據(jù)時程分析的模擬結(jié)果可以了解到，在選取的兩條地震波作用下，兩種形式的鋼框架電梯井道結(jié)構(gòu)層間位移相對比較接近，直梁形式的鋼框架電梯井道結(jié)構(gòu)頂點位移較小。相比之下，傳統(tǒng)形式的直梁電梯井道結(jié)構(gòu)形式抗震性能更勝一籌，因此，在一些地震高發(fā)區(qū)建議使用直梁鋼框架電梯井道。此外，弧形梁在制作方面相比直梁也較為麻煩。