三元多項式展開式系數、冪、最短路經之間的聯系
2021-06-11 19:27:35任茜鈺王楠沈稷倫任澤慧
錦繡·下旬刊 2021年1期
任茜 鈺王楠 沈稷倫 任澤慧

摘要:雖然楊輝三角針對兩個未知數和的多次方運算說明了它與系數的相應關系及最短路徑之間的關聯,但其對于三個未知數的多次方并沒有簡便算法可以快速計算。此文在于拓展楊輝三角內容,可以做到快速拆分三個未知數多次冪的式子。
關鍵詞:楊輝三角;多次系數;三維;最短路徑
1 三元多項式及其系數的關系
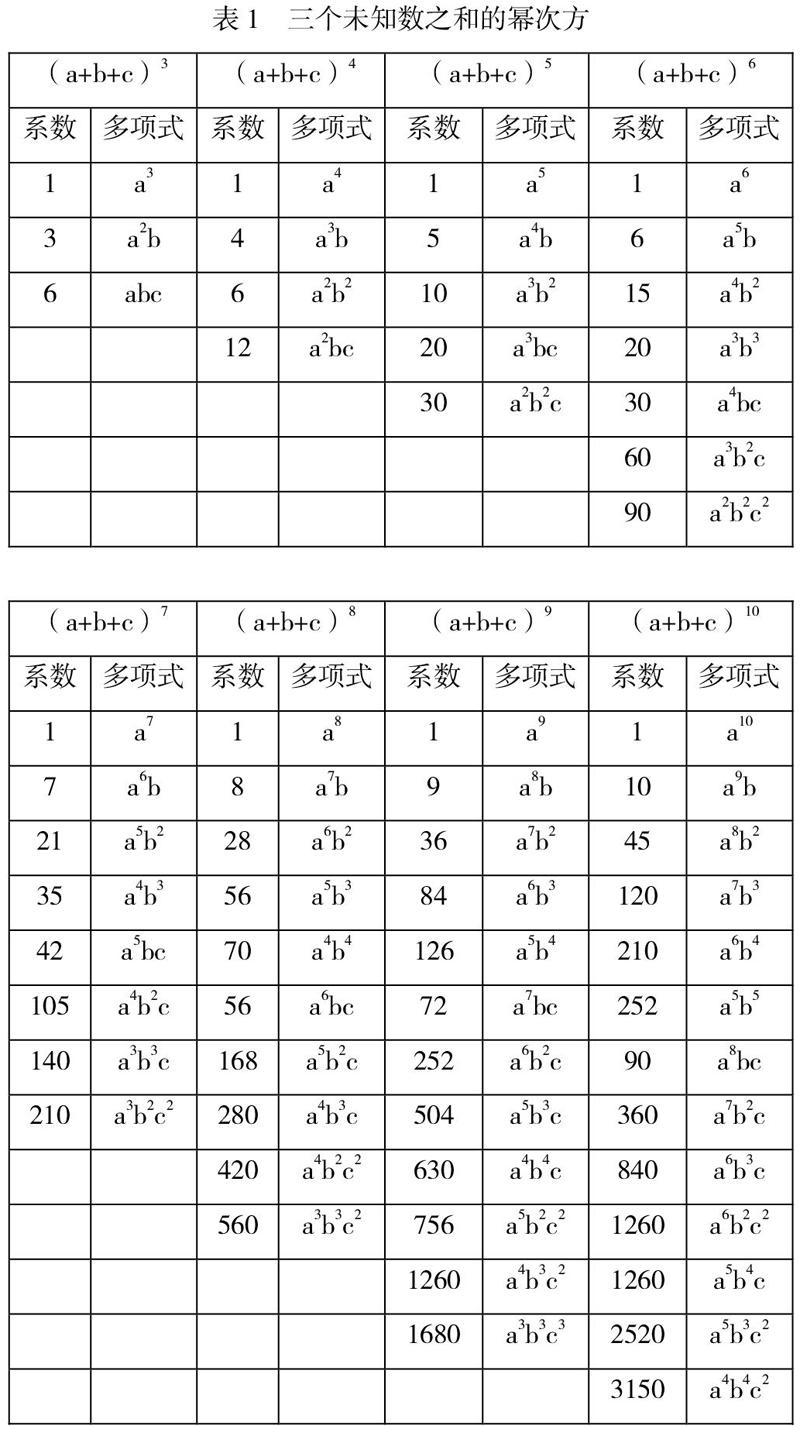
楊輝三角具有對稱性,而前人已經證明。驗算出的式子如表1所示。觀察每項未知數的指數,可以得到項的分組規律:若有m個未知數的n次方的算式,以一個未知數為一組,從最高指數n開始依次遞減,到m個未知數指數相同或相鄰為止,m個未知數便是m組,系數從小到大依次排序,且某項指數越集中到一個未知數,系數越小。
2 系數之間的關系
將兩個未知數的N次方系數取二分之一(第一行),三個未知數的N次方取三分之一(第二行),如圖1所示。
觀察圖1可得到此任式定理:
其中第一個C式為原二項式,T式本文定義為三項式增量,三元n次多項式系數開始滿足于二項式,直到n=2m為止。
3 系數與最短路徑的關系
如圖2所示,如a2bc,那么對應的坐標便是(2,1,1),則此點的最短路徑數便是系數12,在x,y,z軸上的平面仍滿足二項式定理,而三維圖形內部的數值則為與之相連的數值之和。
4 結論
本文經過推理和研究,得到了關于三元N次方系數與多項式之間的關系,通過計算后本人也發現了多元N次方同樣有此規律。
(遼寧工程技術大學軟件學院?遼寧省?興城?125105;阜新市實驗中學;3.撫順市四方高級中學)

