周期荷載激勵下覆冰輸電線的舞動特征研究

楊曙光,劉小會1,,梁浩博,蔡萌琦

(1.重慶交通大學 省部共建山區橋梁及隧道工程國家重點實驗室，重慶 400074；2.重慶交通大學 土木工程學院，重慶 400074；3.成都大學 建筑與土木工程學院，成都610106)

在如今這個信息化的時代里，電能早已成為了人們日常生活中不可或缺的一部分，因此輸電線路的安全穩定運行就十分重要。在惡劣的自然環境中，雨雪冰凍天氣容易使得輸電線覆冰，覆冰輸電線在外部風的激勵下又容易產生單個或多個半波大振幅、低頻率的舞動[1]。輸電線舞動又會產生跳閘、斷股、輸電塔倒塌等事故。為了使電力能源遠距離安全、穩定地傳輸，輸電線路的非線性舞動特征研究是十分有必要的。

早在1932年國外學者Den Hartog[2]就提出了垂直舞動機理，研究發現覆冰輸電導線舞動橫向幅值遠小于豎向幅值，表明舞動主要發生在豎直方向，并在同年提出了鄧哈托判別準則。Desai等[3]在鄧哈托判別準則的基礎上，運用有限元方法研究相鄰跨會對舞動幅值產生的影響；在此基礎上，Rega等[4]運用攝動法求解了弱激勵下的非線性偏微分方程，分析了幅頻函數圖像的多值性，然而以上論文均沒有考慮空氣動力荷載。此外，1983年，Luongo等[5]考慮彈性電纜的非線性運動學關系推導出了連續非線性方程，并研究了輸電線舞動風速和相應參數的關系及其氣動穩定性；曹化錦等[6]運用ANSYS建立了輸電塔及輸電線的有限元模型，對不同風況的輸電塔和輸電線耦合體系進行了舞動仿真，得到了舞動振幅和輸電塔的動力響應；張棟梁等[7]采用Hamilton原理建立了4自由度非線性舞動方程，提出了一種新的覆冰輸電線舞動分析的有限元模型。然而以上論文沒有考慮相鄰檔導線之間的影響。王建軍等[8]用數值方法研究了單自由度參數振動系統在外荷載激勵下多頻響應的非線性特征；黃坤等[9]研究了梁索耦合結構在高頻激勵、低頻激勵和高頻與低頻組合激勵下幅值隨激勵參數變化的規律；趙躍宇等[10]對參數激勵下斜拉索主參數共振的穩定性分析表明固有頻率和外激勵參數對斜拉索穩態解和穩定性存在直接影響。然而以上論文對于索的研究沒有考慮氣動荷載對輸電線的負阻尼影響。郝淑英等[11]建立四分裂覆冰輸電線周期振動的非線性動力學偏微分方程，揭示了輸電線在舞動過程中會出現固有頻率漂移的現象；劉海英等[12]建立了覆冰四分裂導線連續體非線性動力學模型，運用數值模擬和理論分析發現非線性因素會使得振幅對頻率產生影響。然而以上論文研究了輸電線在氣動荷載的舞動特征，并未同時考慮周期激勵和氣動荷載對輸電線的影響。

長期以來，科研工作者對輸電線舞動做了深入的研究，然而對于考慮動態風對覆冰輸電線的作用和考慮相鄰檔對舞動檔的影響是比較少的。本文考慮覆冰輸電線由于受到動態風與相鄰檔的影響存在周期激勵的一般性，將施加有空氣動力荷載和周期激勵的覆冰輸電線作為研究對象，運用多尺度法求出該系統的解析解；對解析解和數值解進行精確度比較，并且分析風速、張力、彈性模量的變化對覆冰輸電線幅頻曲線的影響。

1 輸電線舞動力學模型

對于平原地區的覆冰輸電線，大部分檔的導線可視為等高差輸電線，因此本文選取兩端固定支座的等高差單檔輸電線作為研究對象。通常風都是不穩定的，本文在靜態風的基礎上添加周期激勵，將覆冰輸電線看作受到一個有動態影響的風荷載；并且選取最危險工況認為風沿水平方向且與導線的軸向垂直，所建立的單檔導線舞動的力學模型如圖1所示。(x，y)為平面直角坐標系，s表示曲線的自然坐標。覆冰輸電線檔距為L，其變形可分為兩個階段進行描述：(1)僅在重力作用下的靜止狀態時，平衡狀態的構形為ξ1，垂度為d。(2)輸電線覆冰后，在風的激勵下，輸電線在O-xy平面發生豎向振動，由初始構形ξ1經過一段時間后變化為ξ2（僅考慮豎直向振動）；由此豎向振動所引起的x、y方向上的動位移可分別表示為函數u(s，t)，v(s，t)，p*cos(Ωt)為自激-受迫系統中的受迫激勵項，將受迫項中的激勵幅值p*考慮成施加在覆冰輸電線豎直方向的均布荷載，并且本文取圖1中微段ds作為輸電線在靜止狀態下的研究對象。

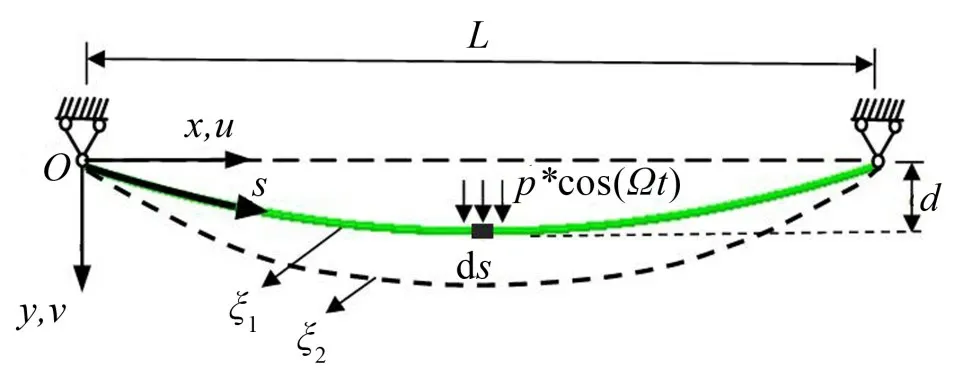
圖1 輸電線平面圖

如圖2所示，輸電線覆冰后，其橫截面形狀從原有的圓形變成了新月形。選取圖1中覆冰導線微段ds的橫斷面作為研究對象，以未產生振動時微段的質心平衡位置作為參考坐標系O1-zy，且振動中心為O1；其中O1z為水平軸，p*cos(Ωt)為受迫激勵項。平均風U作用在覆冰輸電線上會產生向上的升力Fy=ρU2hCy/2，豎直向的空氣動力系數可擬合為Cy=A′α+B′α3，其中代表運動狀態變化的攻角α=/U，表示水平風作用于覆冰輸電線產生的豎直向振動速度，并且A′和B′表示豎直向空氣動力擬合系數，則升力Fy[13]：

圖2 輸電導線橫截面圖

式中參數分別為

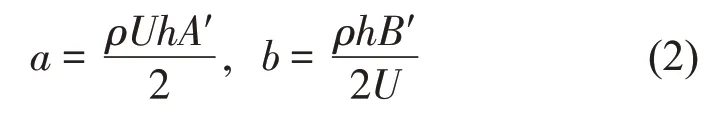
式中：ρ表示空氣密度，h表示輸電線的直徑。

輸電線屬于大跨度的柔性索結構，針對這種類型的結構，可做出如下假設：

(1)在靜止狀態下，輸電線的重力平衡曲線可以通過拋物線y=4d[x/l-(x/l)2]來描述。

(2)假設H為導線靜態下初始張力的水平分量。

對于研究的小弧垂輸電線，結合圖1只考慮靜態風作用下輸電線豎直方向運動的控制方程為[4]

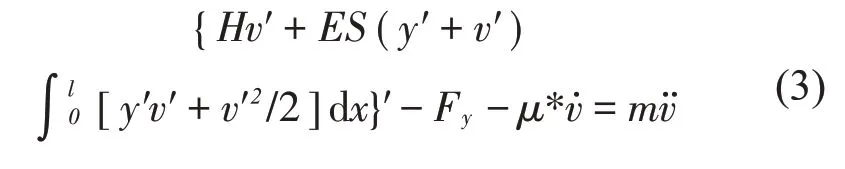
式中：E表示輸電線的彈性模量，S表示輸電線的橫截面積，m表示單位長度的質量，μ表示結構阻尼，y′表示拋物線方程對x的一次導數，v′表示豎直方向運動函數對x的一次偏導，表示豎直方向運動函數對時間t的一次導數，表示豎直方向運動函數對時間t的二次導數。

輸電線在自然環境下，受到自然風作用下也會產生舞動。式(3)模型的建立主要是針對靜態風U，而自然風可以表示成平均風U和脈動風(t)的疊加。在工程分析中，可以采用諧波疊加法進行脈動風荷載模擬，利用譜分解和三角級數疊加來模擬脈動風的隨機過程，將隨機信號通過傅里葉分析變換得到一系列不同頻率和幅值的正弦波或其他諧波[14]，即可以表示出自然風對覆冰輸電線的氣動力表達式：

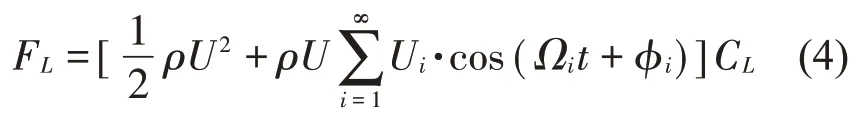
式中：Ui為每個諧波成分對應的幅值，Ωi和φi為脈動風變換后對應諧波項的圓頻率和相位差，并且忽略了氣動力的高階小量。自然風中穩定的部分使得輸電線產生自激振動，不穩定的部分會引起外部激勵[15]。自然風對輸電線的氣動力如式(4)所示。其中存在諧波激勵項，因此可以在傳統穩定風作用下的輸電線舞動方程基礎上添加周期激勵來模擬動態氣動荷載對輸電線的作用。此外，如果考慮相鄰檔導線的影響，則相鄰檔導線也會給舞動檔導線施加一個周期激勵，如圖3所示。

圖3 輸電線平面圖

圖3中Δx是相鄰導線運動導致的端部位移，ξ3原始導線的構型，ξ4為運動后導線的構型。忽略輸電線橫向變形及幾何非線性引起的附加彈性動張力，可以容易給出上述導線的運動控制方程：

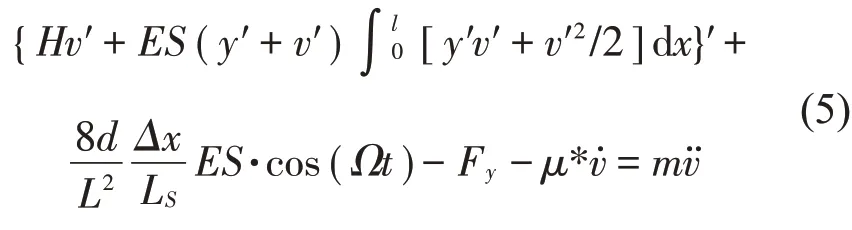
式中：8dESΔx·cos(Ωt)/(L2LS)表示端部周期位移的激勵項，該端部位移是相鄰檔導線舞動所產生的[16]，其中Ω為端部位移激勵的圓頻率，Ls=L[1+8(d/L)2]為考慮垂度的輸電線長度。

自然風對輸電線的作用，自然風中的平均風使得覆冰輸電線發生自激振動，脈動風使得覆冰輸電線發生受迫振動；結合脈動風與相鄰檔對舞動檔的影響來考慮，將原有空氣動力荷載和周期激勵組合來進行模擬。在本文中為了使公式具有一般意義，主要研究外部激勵的參數變化對舞動特征的影響。那么對式(3)添加如圖2中的簡諧激勵p*cos(Ωt)后得到自激-受迫系統的控制方程：

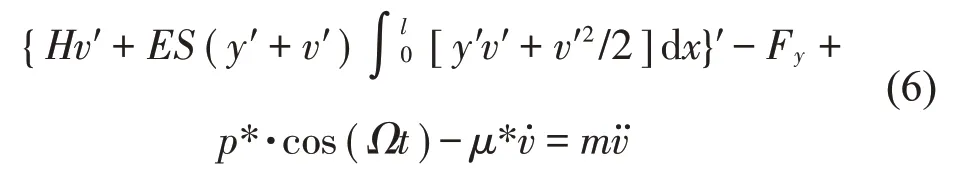
采用模態疊加法將v(x,t)表示為模態函數f(x)和時間函數q(t)的乘積：

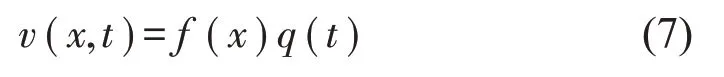
將式(7)代入式(6)后可得到一個非線性常微分方程，則豎直向運動函數對x和時間的導數分別為，其中模態函數為f(x)=sin(nπx/L)，令n=1，即以研究1階陣型為主。為了使方程便于計算，采用Galerkin方法將方程化簡得到覆冰導線舞動的振動動力學方程：

式中的參數分別為

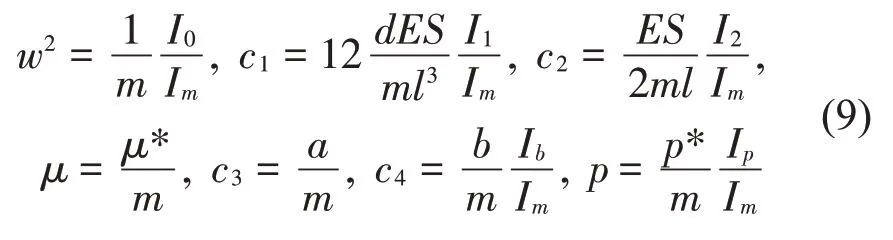
對于式(9)，參數w為輸電線系統的固有頻率；由于p*考慮成豎直方向的均布荷載，因此受迫項的模態函數f1(x)=1，I的值取決于模態函數f(x)，其定義如下：

在式(8)中，針對弱非線性系統，對振幅進行限制，可以對阻尼項和非線性項作如下轉換：

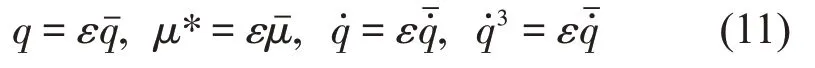
式中：ε是與時間有關的小量為系統新變量，為了公式簡潔，后文仍用q、μ、來表示。將式(11)代入式(8)中可得弱激勵下接近共振的自激系統：

2 非線性舞動方程解析解求解

2.1 弱激勵下的自激系統

對于弱非線性系統式(12)，即為接近共振的受迫振動，取ε=0.1，偏微分算子符號、受迫項頻率以及振幅可以劃分為

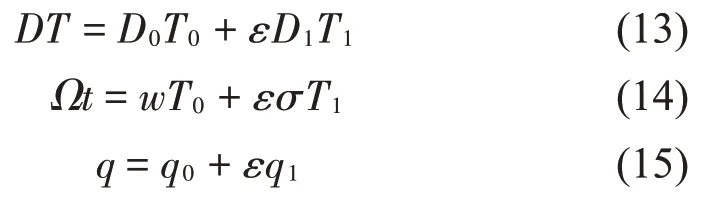
式中：σ為激勵頻率的調諧參數，將式(13)、式(14)和式(15)代入式(12)后，比較ε同次冪系數后得到一組關于εn(n=0，1)線性偏微分方程：

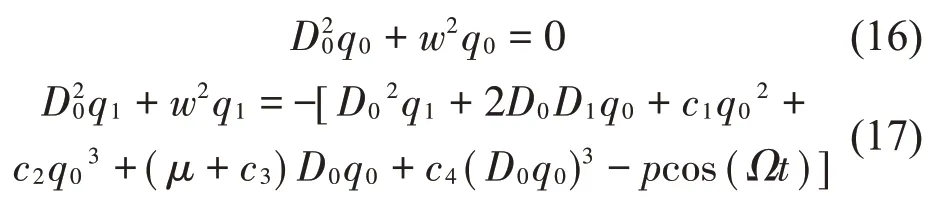
式中：Dk表示對Tk求偏導數，求解式(16)得到：

式中：A可定義為

將式(18)和式(19)代入式(17)，分離久期項得到對應的1階微分算子，然后再分離微分算子的實部和虛部可得到系統振幅和相位的變化率方程：

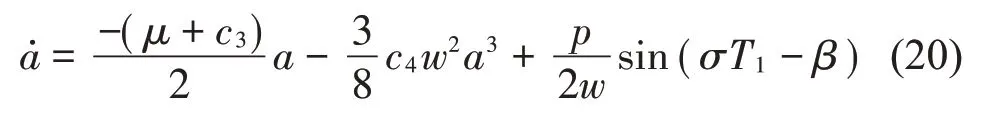
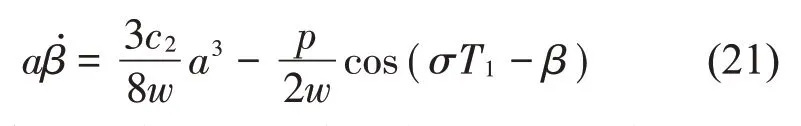
為了確定穩態運動定常解的振幅和相位，引入γ=σT1-β,令D1A=0，然后消掉γ得到幅頻響應方程：

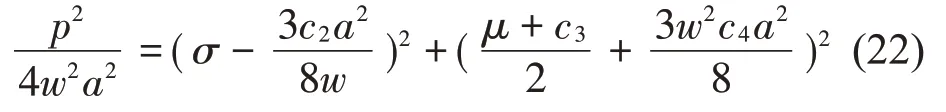
2.2 強激勵下的自激系統

將式(12)改寫為遠離共振的受迫振動，則舞動方程為

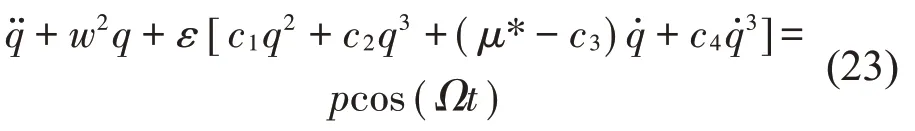
將式(13)、式(14)和式(15)代入式(23)，其中式(23)Ωt=ξT0+εσT1，然后按照相應小量階次進行劃分可得到一組關于εn(n=0,1)線性偏微分方程：

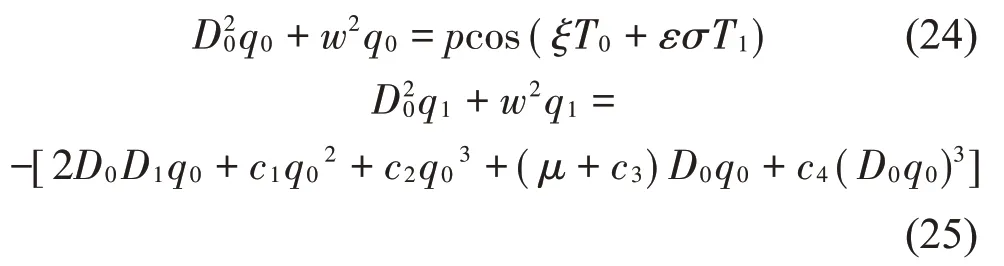
式中：Dk表示對Tk求偏導數，式(24)的解為

式(26)中A和B可分別表示為

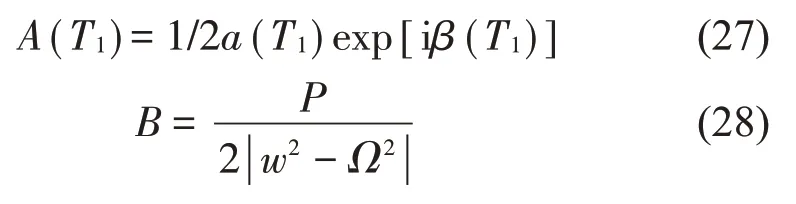
將式(26)代入式(25)得到：

限于文章篇幅，對于式(29)，先不考慮諧波共振，因此為了防止產生超諧波和次諧波共振項，取Ω=w/4。結合式(27)、式(28)和式(29)分離久期項得到對應的1階微分算子，然后再分離微分算子的實部和虛部可得到系統振幅和相位的變化率方程：

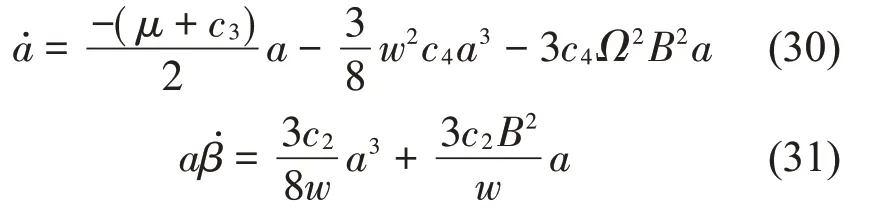
對式(31)進行時間積分后可得到：

對于幅值函數a(t)的表達式，其中m和n取決于輸電線的物理結構參數和氣動參數，并且m決定了振幅的變化趨勢。

當外激勵比較弱時，自激-受迫系統中存在有自激振動，即滿足存在自激振動的充分必要條件為

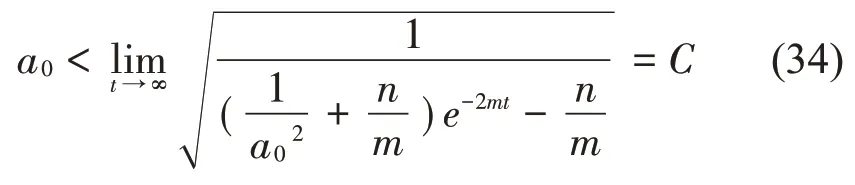
此時滿足參數m＞0，那么式(32)即為收斂的情況，激勵幅值滿足式(34)的條件，此時系統仍然可以形成自激振動，不會破壞自激振動的條件，系統的穩態運動就由自激振動和受迫振動疊加而成。

當外激勵比較強時，m＜0，即破壞自激振動的條件為

激勵幅值不滿足式(34)的條件，那么自激振動振動幅值隨著時間變化趨近于0，激勵幅值符合式(35)的條件，則無法形成自激振動，表明此時自激-受迫系統中不存在自激振動。式(32)、式(34)和式(35)中各參數分別為

3 數值解與解析解分析

輸電線覆冰后，冰型對氣動力也存在很大的影響，因此選用具有代表性的新月形作為研究對象。為了便于分析比較，選用文獻[17]的幾何參數、材料參數和相應的氣動力參數如表1所示。

空氣動力荷載作用下的覆冰輸電線，經過物理建模和數學分析得到運動狀態下的偏微分控制方程，運用模態疊加法和Galerkin法得到舞動常微分方程式(8)。如圖4所示。使用表1的數據并且給輸電線施加豎向的初始擾動后，令初值豎向擾動q(0)=0.01 m，并且將激勵幅值p*=0.186 8 N/m代入式(8)中，計算的步長取1/10，用MATLAB求解式(8)得到覆冰輸電線舞動時中點的豎向位移時程圖像。在1 725 s后振動幅值趨于穩定；局部放大圖為幅值穩定后2 000 s～2 020 s的時程位移曲線。從圖4中可以看出，施加受迫激勵幅值穩定后的時程位移圖，其幅值隨時間變化會產生向上或者向下不規則的抖動，主要是由于周期激勵項的頻率與系統固有頻率不一致而造成的。

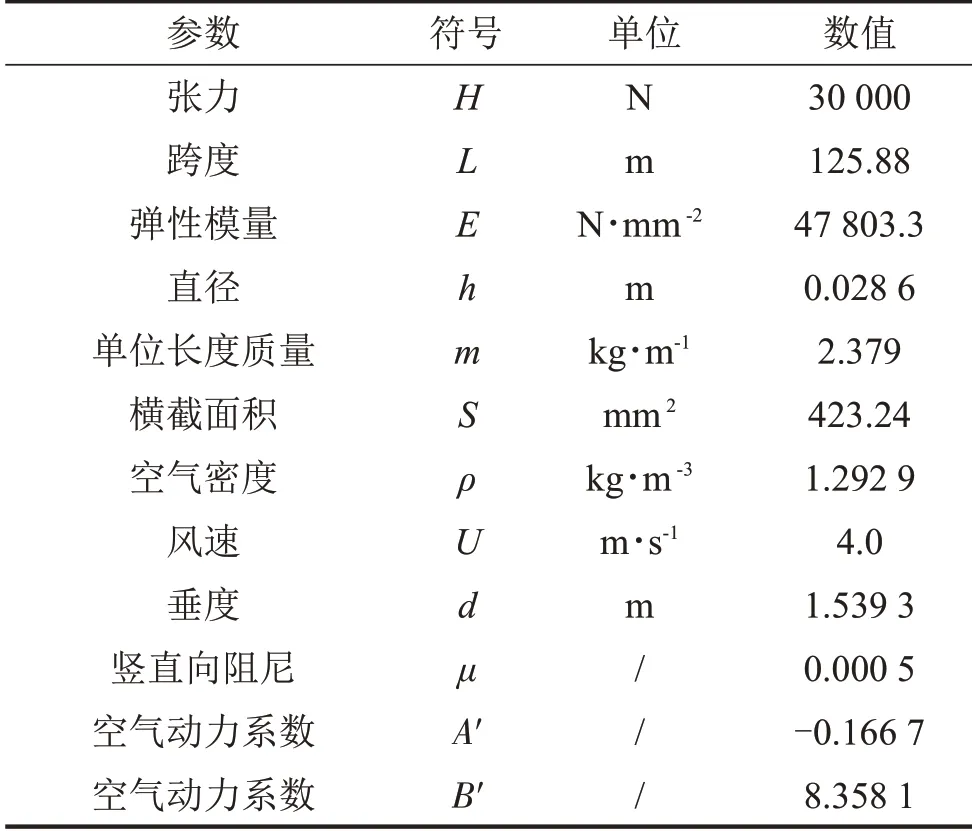
表1 覆冰輸電線線路物理參數

圖4 位移時程圖

在自激-受迫振動系統中，既存在平均風的氣動荷載激勵，又存在脈動風與相鄰檔影響的周期激勵。圖5是使用Maple軟件繪制自激-受迫系統的振幅解析解式(32)得到的，其中曲線b、c、d、e分別對應激勵幅值p*=0.934、3.736、9.343、14.948 N/m中自激振動的幅值變化；激勵幅值增大，使得空氣動力荷載下覆冰輸電線的自激振動的幅值越來越小；隨著激勵幅值的增大，自激振動幅值曲線達到穩定的時間也不斷延長；圖5中曲線b、c、d即在判別式(34)的范圍內，曲線e在判別式(34)的范圍外，隨著激勵幅值p*=0.934 N/m對應的曲線b增加到p*=9.343 N/m對應的曲線d，響應幅值從點ab下降到點ad；當激勵幅值p*=14.948 N/m時，響應幅值趨緊于0，即表現為該自激-受迫系統中不存在自激振動的形式。

圖5 受激勵幅值影響的自激振動幅值曲線

隨著激勵幅值的增加，氣動荷載激勵下的覆冰輸電線自激振動條件被受迫激勵所破壞，這種現象稱為猝息。

對于施加受迫激勵的自激系統，多采用幅頻和相頻響應曲線進行分析。為了驗證本文幅頻響應關系式推導結果的正確性，令激勵頻率Ω等于系統固有頻率w，調諧參數σ=-0.8、0、0.8，用數學軟件Maple繪出式(22)的幅頻響應曲線。運用MATLAB求解式(8)得到激勵幅值p*=3.736、7.472、11.210、14.948、18.68 N/m時的時程位移圖，分別得到穩定時的振幅幅值如圖6中的點a1、a2、a3、a4、a5。如圖6所示。MATLAB求得的數值解和運用多尺度求得的幅頻響應函數曲線吻合較好；并且發現σ=0.8時，隨著激勵幅值的變化，響應幅值會發生跳躍和多值現象；當響應幅值大于2時，幅頻響應曲線的精確度也會隨著激勵幅值的增大而降低。

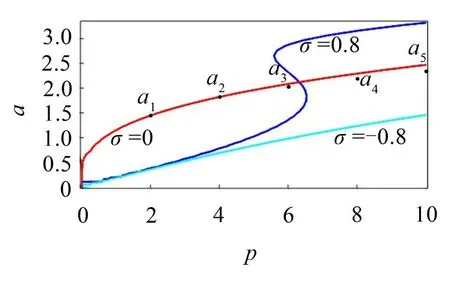
圖6 激勵幅值-響應幅值曲線

4 線路參數分析

風速對覆冰輸電線舞動有非常大的影響，甚至可以決定覆冰輸電線形成自激振動的條件。對于施加弱激勵的自激系統，為了研究其非線性共振特性，用Maple數學軟件繪出方程式(22)的函數曲線。激勵幅值p*=0.186 8 N/m，風速U=4，8，12，16，20 m/s時系統的幅頻響應曲線如圖7所示。實線表示穩定，虛線表示不穩定。隨著風速的不斷增大，響應幅值也不斷增大，從風速U=4 m/s的點p4增加到U=20 m/s的點p20；穩態解的不穩定區域也逐漸變大，從風速U=8 m/s的r1區域依此變化到U=12，16，20 m/s的r2，r3，r4區域；并且導致非線性也不斷增強，自激-受迫系統呈現硬彈簧特性更加明顯。

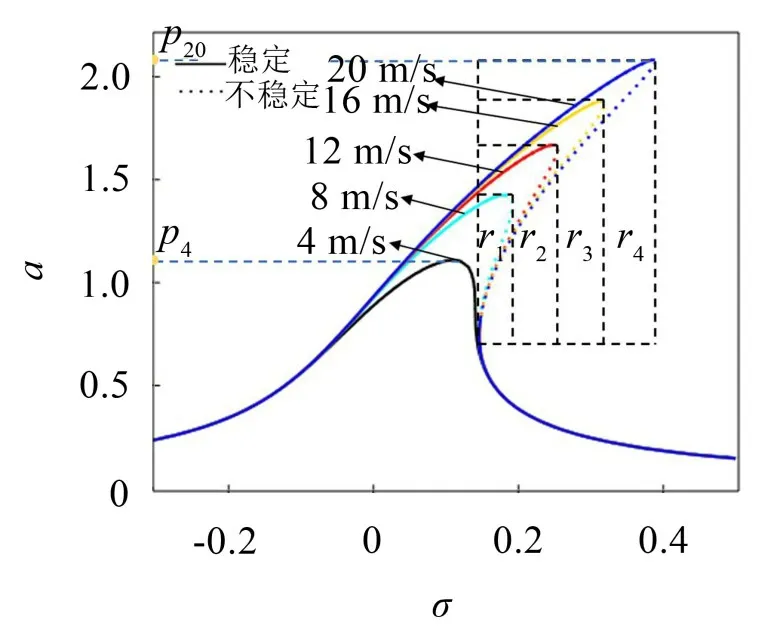
圖7 不同風速的幅頻響應曲線

為了弄清楚激勵幅值對自激振動的影響，令式(22)的激勵幅值p*=1.121、2.802、5.604、14.944 N/m，風速U=4 m/s，受迫激勵項的頻率Ω=w，并且運用Maple得到圖8。

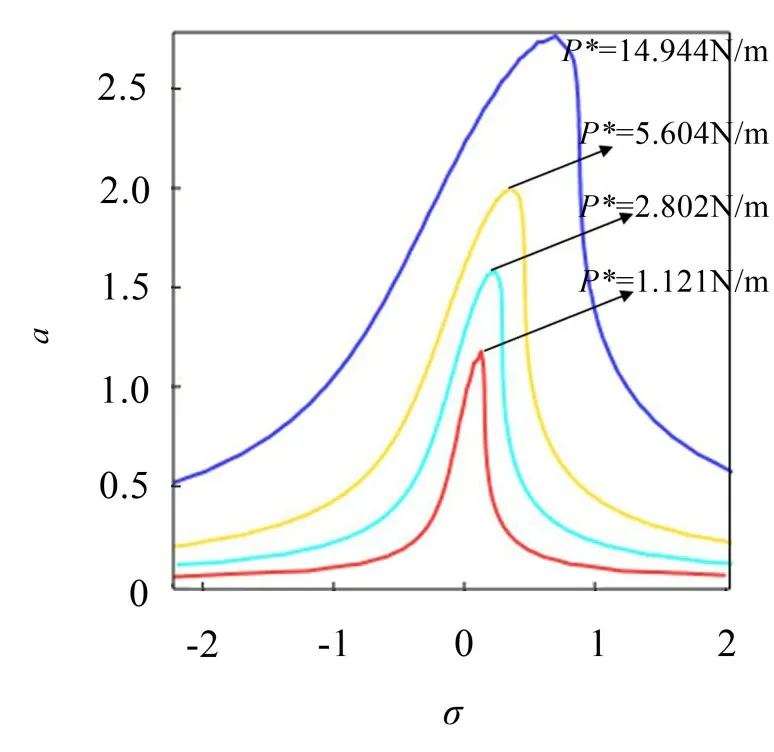
圖8 不同激勵幅值對應的幅頻響應曲線

如圖7所示。隨著激勵幅值增大，系統的響應幅值也逐漸增大，也就表明周期荷載激勵項對響應幅值有著直接的影響。

風速和激勵幅值的增大，都能使得響應幅值增大；由于風速表現為非線性舞動方程中負阻尼項，因此風速的增加又使得覆冰輸電線舞動的非線性特征增強。

為了分析在相同線路參數和相同氣動荷載情況下張力和垂度對覆冰輸電線舞動特征的影響。取激勵幅值p*=0.934 N/m，風速U=4 m/s；引用文獻[18-19]中垂度與張力之間的公式d=mgl2/8H，取張力分別為H=15 000、20 000、25 000、30 000、40 000、50 000、60 000、70 000 N，分別對應于圖9中A、B、C、D、E、F、G和H幅頻曲線。使用MAPLE繪出式(22)的函數曲線，得到不同張力對應的幅頻響應圖。如圖9(a)所示，隨著張力從15 000 N增大到30 000 N，響應幅值從a15增加到a30；如圖9(b)所示，隨著張力從30 000 N增大到70 000 N，響應幅值a30從減小到a70；張力由小變大，垂度不斷變小，自激-受迫系統的響應幅值出現先增大，后減小的現象，因此在工程應用中，適當增加輸電線的張力可以減小覆冰輸電線的舞動幅值。

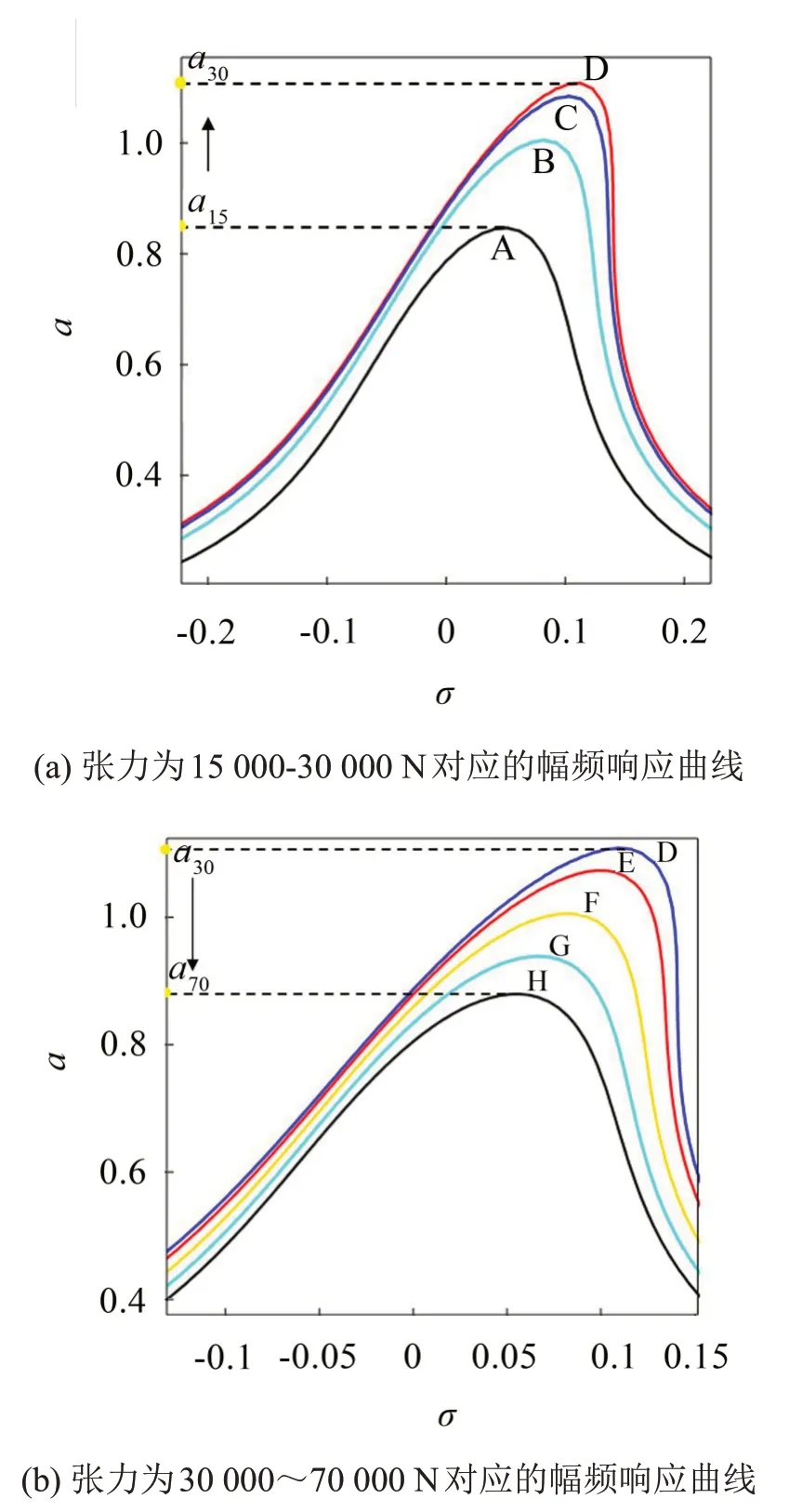
圖9 不同張力對應的幅頻響應曲線

為了分析輸電線彈性模量變化對弱激勵下自激系統的非線性特征影響，對于幅頻函數式(22)，取張力H=30 000 N，垂度d=1.539 3 m，激勵幅值p*=0.934 N/m，風速U=4 m/s；彈性模量為：E=9 560.7、47 803.3、239 016.5、478 033、2 390 165 N/mm2，分別對應著圖10中A、B、C、D、E曲線。如圖10(a)所示，彈性模量由小變大，輸電線結構剛度不斷增加，輸電線舞動的幅值逐漸減小，使得自激-受迫系統非線性增強趨向于硬彈簧特征；隨著彈性模量增大到239 016.5 N/mm2即曲線C時，系統的非線性特性隨即開始減弱，幅值也隨著變小，然而響應幅值產生跳躍、多值和不穩定現象。

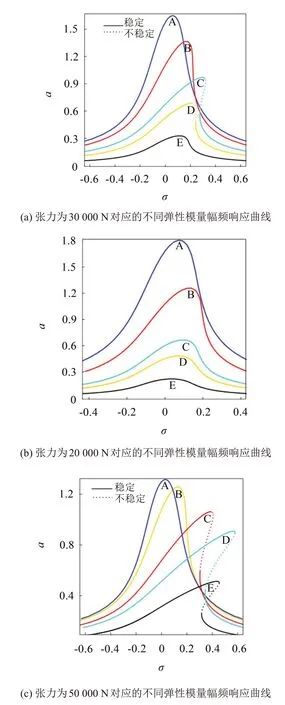
圖10 不同彈性模量和張力對應的幅頻響應曲線

為了弄清楚輸電線不同張力情況下，彈性模量變化對自激-受迫系統非線性特征的影響，如圖10(b)，取張力H=20 000 N，d=2.309 0 m；如圖10(c)，取張力H=50 000 N，垂度d=0.923 6 m。彈性模量E=9 560.7 N/mm2對應圖10中曲線A的共振峰值，其中圖10(b)的共振峰值最大，圖10(c)的峰值最小；彈性模量E=478 033 N/mm2對應圖10中曲線D的共振峰值，然而圖10(c)的共振峰值最大，圖10(b)的共振峰值最小；則表明在相同的線路參數、環境參數、以及相同彈性模量范圍內，張力越大，響應幅值變化幅度越小。

從圖10中也可以看出，從張力為20 000 N的圖10(b)到張力為30 000 N的圖10(a)，再到張力為50 000 N的圖10(c)，隨著彈性模量的增加，自激-受迫系統的硬彈簧特性也更加明顯，響應幅值產生跳躍、多值和不穩定的現象增加。

彈性模量的增大能有效降低輸電線舞動的共振幅值；增大彈性模量，同時增大輸電線的張力，也能降低輸電線舞動的共振幅值，然而隨著張力的增大，自激-受迫系統的響應幅值出現了跳躍、多值和不穩定的現象。

5 結語

(1)當自激-受迫系統中激勵幅值不斷增大，其中自激振動幅值會越來越小甚至消失出現猝息現象，自激-受迫系統由自激振動和受迫振動疊加的振動形式轉變為受氣動荷載負阻尼影響的受迫振動。

(2)對于自激-受迫系統，風速的不斷增大，使得系統呈現硬彈簧特性，并且導致系統非線性也不斷增強，不穩定區域也逐漸變大；輸電線張力和彈性模量同時由小變大，輸電線結構剛度不斷增加，也能有效地減小輸電線舞動共振幅值，然而該系統也伴隨著非線性特征的出現；因此適當增加輸電線張力和彈性模量有利于減小輸電線舞動的共振幅值。