基于遺傳算法的電磁分流阻尼參數優化

李戈，毛崎波，吳彬

（1.南昌航空大學，南昌 330063；2.中國科學院 力學研究所，北京 100190）

電磁分流阻尼技術是利用機電能量轉換特性來耗散被控對象的機械能的控制方法[1-2]，其原理是當被控對象發生振動時，線圈與永磁鐵存在相對速度，根據法拉第電磁感應定律，線圈內會產生感應電流以及感應磁場，永磁鐵與線圈之間會產生電磁力以阻礙這種相對運動[3]。電磁線圈外接分流電路構成電磁分流阻尼，電磁分流阻尼通過分流電路耗散由主系統的機械能轉化而來的電能[3-4]，常見的分流電路有RL電路，RL-C電路[5]。RL電路常用于控制低頻率的振動，因為隨著頻率增加，感抗隨之增加，電流分量隨之減小，無功功率增加，導致控制效果減弱。而加入電容組成LCR分流電路是因為電容上的電壓相位與電感上的相位相反，而LCR串聯諧振電路可以通過調節電容的大小來降低電路無源阻抗，從而降低無功功率。相比較之下LCR分流電路能獲得更好的控制效果。電磁分流阻尼技術可以應用于多種結構，單自由度的LCR電磁分流電路優化是其理論基礎，因此將電磁分流阻尼用于控制單自由度系統振動的研究值得重視。

利用定點理論求解隔振器或者動力吸振器的最優化問題也稱H∞優化[6-16]，不但可以推導出動力吸振器的最優設計，而且還可以用來推導出電磁分流阻尼的最優設計參數。定點理論的缺點在于只能針對主系統無阻尼的情況來進行優化，而主系統阻尼比不為零，則位移放大因子的曲線將不會相交于兩個定點[7]。對于含有電磁分流阻尼的隔振器或者調諧質量阻尼器(TMD)，應用定點理論設計最優參數，若考慮主系統阻尼,使用定點理論同樣不具有可行性。當主系統被作用于電磁分流阻尼時，位移放大因子隨頻率比變化的曲線存在多個極值點，因此需要使用一種不容易陷入局部優化的算法，而遺傳算法作為一種內在啟發式隨機搜索算法，在搜索的最優解的過程中不容易陷入局部最優[8-16]。因此本文使用遺傳算法求解考慮主系統阻尼比時電磁分流阻尼的最優設計參數。Nariman等[8]使用多目標遺傳算法優化了5自由度車輛振動模型，并得到了pareto解；Esen等[9]使用遺傳算法優化了針對的槍管筒體式動力吸振器的參數；Lee等[10]使用遺傳算法優化了多重動力吸振器的設計參數。國內的付江華等[11]基于H∞優化的目標函數，使用了包括遺傳算法在內的多種進化學習算法，求得了當位移放大因子含有主系統阻尼比時的傳統動力吸振器的最優阻尼比、最優調諧比。李學斌[12]利用多目標遺傳算法求出了動力吸振器(DVA)的最優參數的pareto解。Xu等[13]使用遺傳算法對精密平臺隔振系統參數進行了優化。故考慮主系統阻尼比時，在求解電磁分流阻尼的優化問題時，本文嘗試使用遺傳算法。

1 電磁分流阻尼模型

1.1 無量綱位移放大因子

本文以LCR串聯分流電路為例，如圖1所示。該系統由主系統質量、阻尼、剛度，以及電磁分流阻尼器構成，可以將音圈電機作為電磁分流阻尼器[15]。

作用于線圈的洛倫茲力為f=φi，該力的方向與音圈電機線圈運動方向相反，并作為一個抑制主系統振動的力與系統的慣性力方向相反，且與電流i的大小成正比。

電磁分流阻尼的力-電耦合方程方程由LCR振蕩電路方程以及主系統運動微分方程所組成。該系統的力-電耦合方程如下：

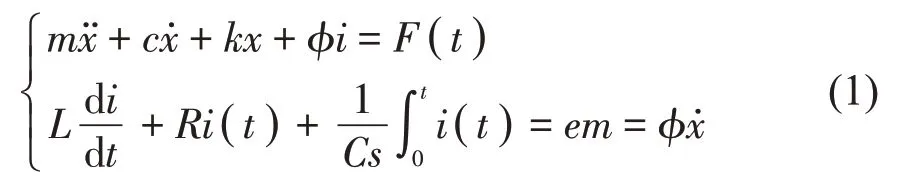
式中：m為主系統質量，c為主系統阻尼，k為主系統剛度，em為感應電動勢，L為線圈電感，R為電磁分流阻尼線路的電阻，Cs為諧振電容；φ為電磁系數，與線圈的匝數、永磁鐵磁場強度、線圈長度有關[5]。

對作復展開，求得幅值為

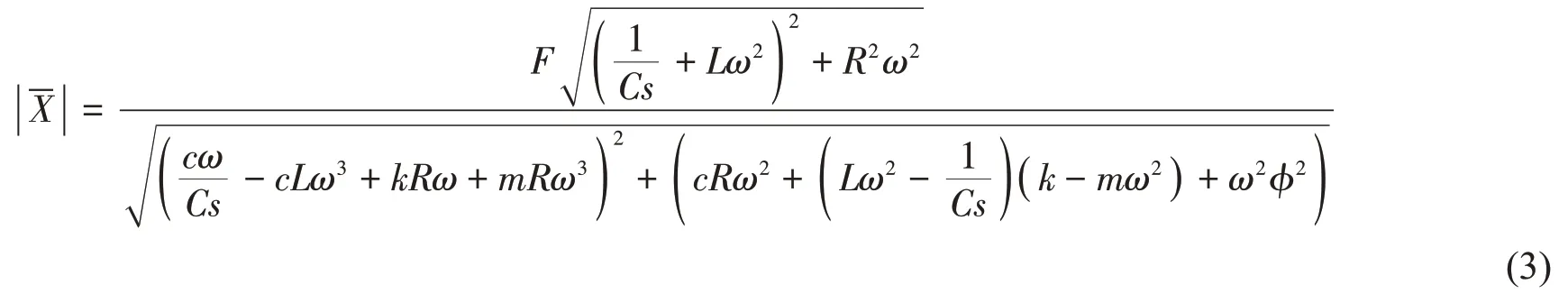
因此位移放大因子的平方根隨激勵力頻率變化表達式為

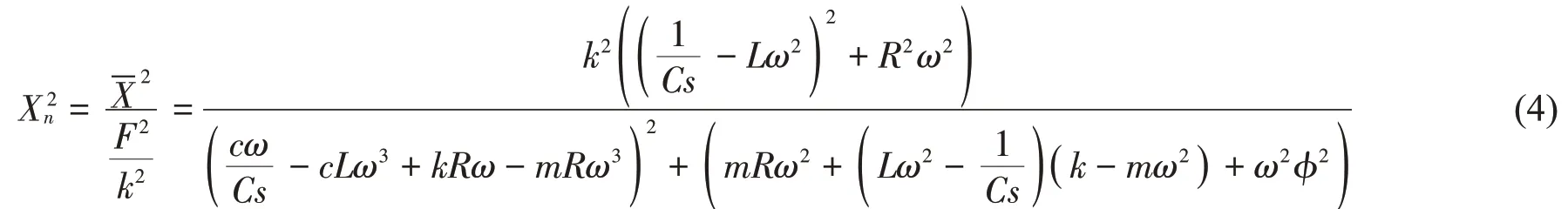
主系統阻尼比為Z=C/2mω0，對式(4)上下同時除以k4L2并再乘以m2，得到無量綱形式的位移放大因子的表達式如下：

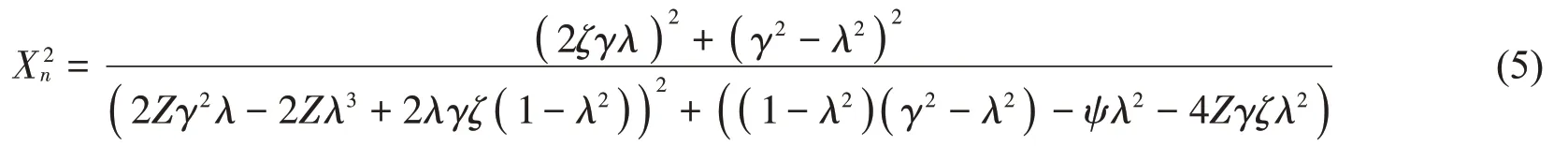
1.2 基于定點理論的最優同調以及最優阻尼條件

令式(5)中主系統阻尼比Z=0得到無阻尼時的位移放大因子表達式如下：

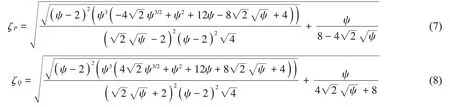
取最優阻尼比ζopt=(ζP+ζQ)/2；將γopt代入γ2=可得到最優電容Copt=由ζopt=可得Ropt=。

2 遺傳算法優化電磁分流阻尼

通過分析PQ定點優化的位移放大因子曲線可知，參數為最優時，曲線上會有兩個極大值點，且兩個極大值點處的高度相同，而當參數不為最優時，兩個峰值一大一小，根據H∞優化的原理，即使得位移放大因子的最大值最小[14]，故設計目標函數以獲取第k次迭代的最大值點，并在種群迭代歷史中搜索最小的那個最大值，對應的調諧比γ，阻尼比ζ即是最優同調條件以及最優阻尼比，因此，可以把目標函數設計為

優化變量的范圍為0≤ζ≤1,0≤γ≤1，用MATLAB編寫優化程序時，首先將頻率比λ在區間0.2＜λ＜1.7離散為數組{λ1λ2,…,λm}，其中離散步長取0.000 5。由于最終是要尋找最小值，因此適應度函數是在數組{γ,ζ,{λ1λ2,…λm}}取的最大值的負數，即適應度函數為

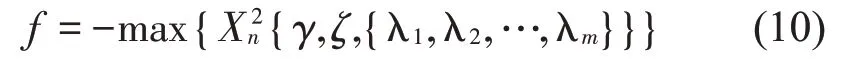
用MATLAB結合遺傳算法優化電磁分流阻尼的步驟為

(1)設定精度為0.000 001，生成0～1隨機數，對調諧比γ、阻尼比ζ的染色體進行隨機編碼，長度為20，初始種群大小設置為500。

(2)對染色體進行解碼，根據式(10)計算適應度值。

圖1 電磁分流阻尼用于控制單自由度振動

(3)對各個染色體的適應度值進行輪盤賭操作，得到個體被選定的概率，并計算累計概率，然后產生一個[0，1]的隨機數來決定哪個染色體可以參與后續的交配[16]，將選中的染色體復制，重復這樣的操作500次，組成新的種群S1。

(4)按交叉率Pc所決定的參加交叉的染色體數c，從種群S1中隨機選定c個染色體，配對并進行交叉，然后將得到的染色體代替原染色體，得種群S2。

(5)根據變異概率Pm確定變異次數m，從S2中隨機選定m個染色體，做變異操作，并用產生的染色體代替原染色體，得到種群S3。

至此，遺傳算法完成了第一代操作流程得到了新的種群，將新的種群作以上同樣的操作，不斷將產生的新種群循環地不斷進行迭代，直到達到預先設定的迭代次數為止，然后輸出最優解以及最優參數如下圖所示。利用遺傳算法優化電磁分流阻尼的流程圖如2圖所示。

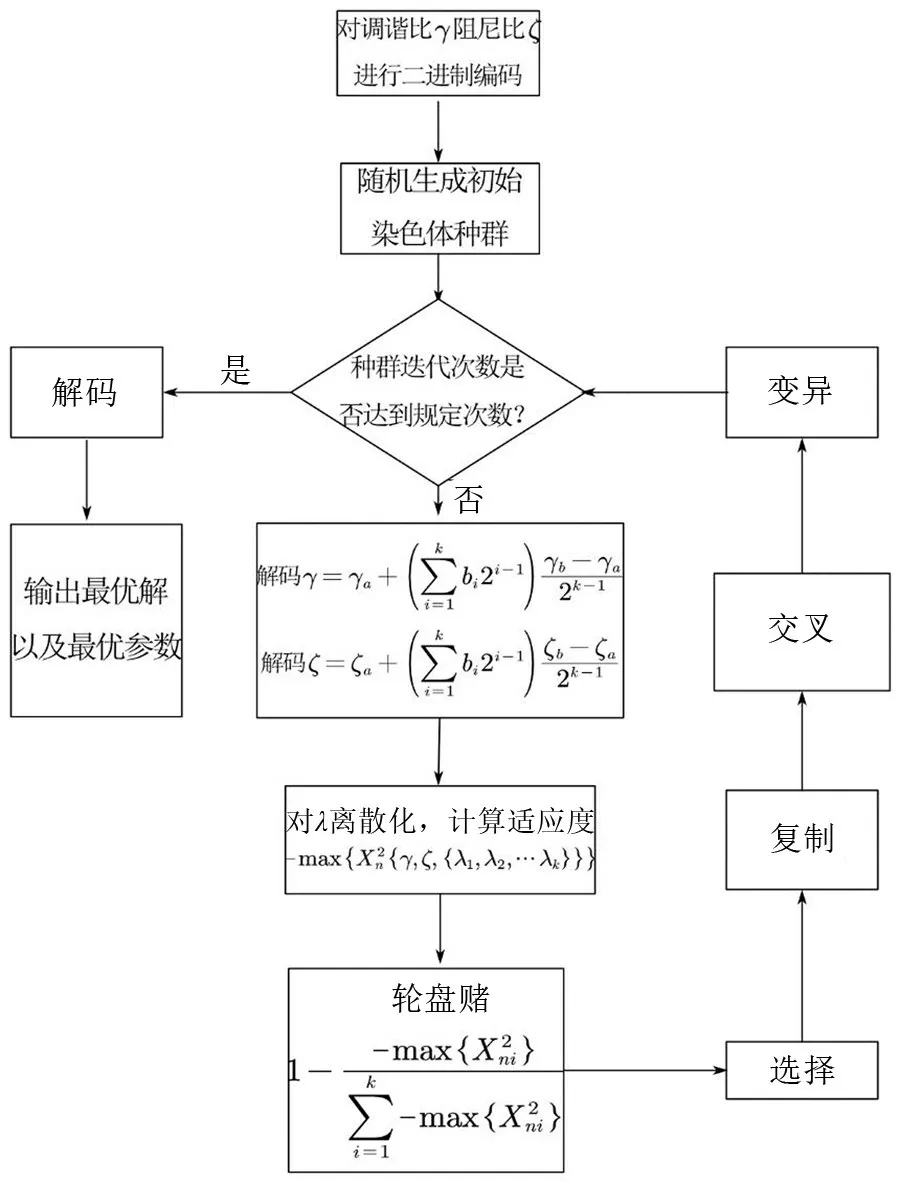
圖2 遺傳算法優化電磁分流阻尼電路的流程圖

3 數值計算

3.1 PQ定點優化電磁分流阻尼

根據參考文獻[5]的數據，對電磁分流阻尼優化所用到的參數的物理意義以及具體數值，如表1所示。

表1 電磁分流阻尼參數

表1中，等效電阻R，與電路電容Cs為待優化變量。根據表1并結合1.2節的結論可以計算出基于定點理論優化最優電容Cs以及最優電阻R分別為Copt=0.020 9 F，Ropt=0.998 54 Ω。

3.2 遺傳算法優化電磁分流阻尼

首先分析遺傳算法優化主系統阻尼比為零時的電磁分流阻尼，再與定點理論優化的電磁分流阻尼進行比較。當主系統阻尼比Z=0，用MATLAB編寫遺傳算法程序計算出,最優阻尼比以及最優調諧比分別為ζGA=0.635 65，γGA=0.816 32；進一步得到遺傳算法優化后的電容Cga=0.020 9 F，Rga=1.058 4 Ω。運行程序可以得到最優個體的適應值隨種群迭代次數變化曲線如圖3所示。

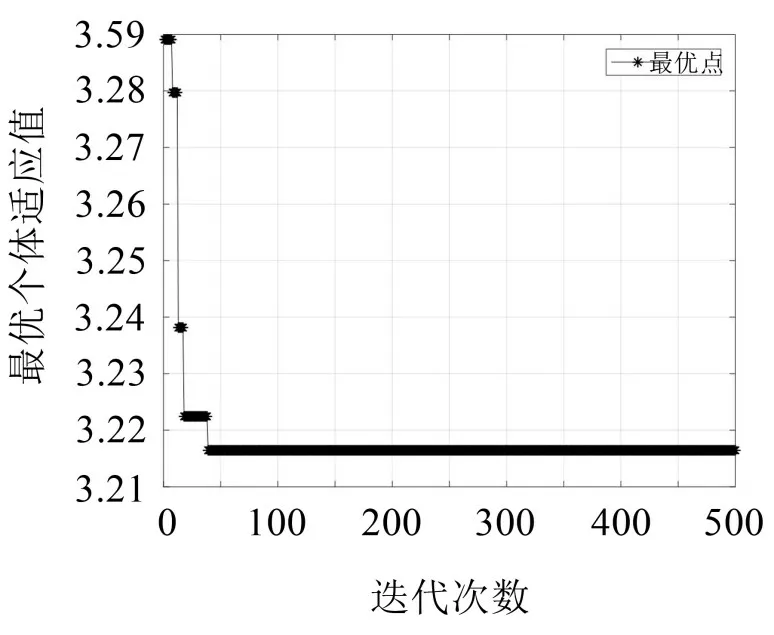
圖3 最優個體適應值隨種群迭代次數的變化趨勢

用MATLAB繪制Xn的響應曲線，并與3.1節計算的PQ定點優化的Xn曲線對比，如圖4所示。

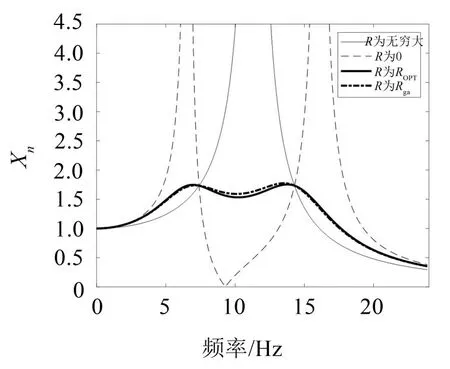
圖4 主系統無阻尼時Rga對應的位移放大因子曲線

分析可知：當主系統阻尼比Z取0時，經過遺傳算法優化后的位移放大因子Xn的曲線與PQ定點優化的曲線存在微弱的差距，這是由于ζopt是取PQ兩點處的阻尼比的平均值，其位移放大因子Xn的兩個極值點并不與PQ定點重合，但是非常靠近，而針對遺傳算法所設計的目標函數是搜索關于位移放大因子Xn的平方根的最大值集合中的最小的最大值，因此才造成這樣的差距。

由于定點理論的缺點是無法針對主系統存在阻尼時對位移放大因子Xn進行優化，因此嘗試使用遺傳算法優化Xn曲線。當主系統阻尼比Z分別為0.01、0.02、0.03時，通過對目標函數的Z值分別進行賦值，運行程序，得到各自的主系統阻尼比所對應的最優調諧比以及最優阻尼比，根據這些參數結合1.2節以及表1的數據，可分別得到主系統阻尼比不同時位移放大因子曲線，如圖5所示。

結合圖5以及表1數據可以得到遺傳算法優化的最優電容Cga以及最優電阻Rga，如表2所示：

圖5 遺傳算法優化阻尼比不同時的位移放大因子

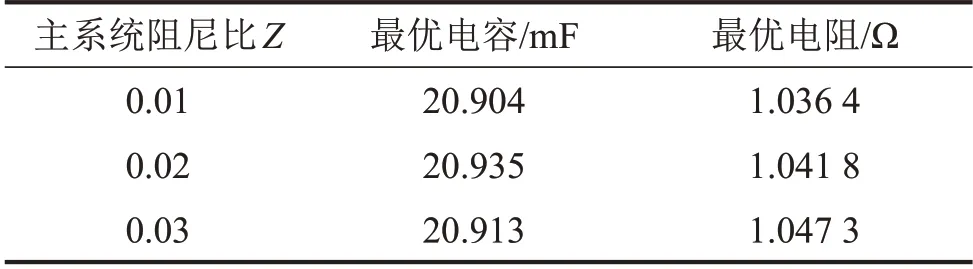
表2 遺傳算法優化后的電容與電阻大小

考慮主系統阻尼后，最優電容Cga幾乎不發生變化即最優調諧比不變，而最優電阻會略微增加，因此相對應的最優阻尼比會增加。

綜合圖4與圖5可知，遺傳算法以編碼方式進行數值計算，不對參數本身進行操作，而定點理論的計算首先要通過解方程的方式求得最優同調條件(即定點等高)，求解最優阻尼比的理論推導過于復雜，因此遺傳算法相對于定點理論具有良好的操作性；而且能考慮主系統的阻尼比，相對于定點理論更能接近實際情況。

為了對比阻尼比取不同值時，遺傳算法的控制效果，令電阻R=109歐姆，則分流電路即可視為斷路，即為控制前的效果。控制效果如圖6所示。

分析圖6可知：未用電磁分流阻尼控制前，位移放大因子Xn的幅值會隨著主系統阻尼比增加而降低；基于遺傳算法優化的電磁分流阻尼設計對降低主系統振動具有良好效果；遺傳算法能解決考慮主系統存在阻尼時，電磁分流阻尼的最優電路參數，目標函數與適應度函數都不用改變，其可操作性更強，并且其控制效果更接近實際情況，因此相比于定點理論具有優越性。

圖6 主系統阻尼比取不同值時，遺傳算法的控制效果

4 結語

本文針對電磁分流阻尼，使用遺傳算法優化所得到的結果基本理想，與定點理論優化的位移放大因子曲線基本吻合，并通過使用遺傳算法解決了定點理論不能優化主系統有阻尼時的電磁分流阻尼電路參數的問題。在應用遺傳算法搜索位移放大因子的最大值時，沒有陷入局部最優，這說明了遺傳算法用于對電磁分流阻尼以及其他含有電磁阻尼的有阻尼動力吸振器的最優設計具有很高的可靠性，且遺傳算法的目標函數以及適應度函數仍然不用改變，這是其便利所在。