非自由聲場中目標聲源粒子速度場的重構

周達仁，肖永雄，盧奐采

（浙江工業大學 機械工程學院，杭州 310023）

近場聲全息技術[1-3]使用布置在聲源近場的全息測量面獲取的聲場信息，重構出結構表面和三維聲場中的聲壓、介質粒子速度和聲強等聲學量的分布，為結構噪聲源的識別定位提供了強大的技術支撐。近場聲全息技術的一般思路是利用齊次Helmholtz方程在各類坐標系下的基本解，即自由空間的格林函數建立結構表面聲學量與場點聲學量、以及各場點聲學量之間的關聯，并建立相應的聲場模型，再通過求解逆問題，將全息測量面上的聲學量映射到重構面。相應地，在具體實施時，聲源則必須置于開放的自由聲場或全消聲的環境中[1]。這一要求使得近場聲全息的實施受到一定程度的限制。為了解決這一問題，研究者在各類近場聲全息技術的基礎上，發展出了相應的聲波分離方法[4-18]。

在建立同時包含目標聲源和干擾聲源輻射的非自由聲場數學模型時，聲波分離方法使用兩組基函數分別對目標聲場和干擾聲場進行建模。相應地，則需使用兩組全息測量值作為算法的輸入量，以求解出兩組基函數系數。常用的測量前端有雙層聲壓測量面[4-8]、雙層粒子速度測量面[9-11]或者單層聲壓-粒子速度聯合測量面[7-8,11-15]。也有研究者使用單層聲壓測量面[16-18]作為測量前端，重構目標聲源的聲壓場，在特定的聲場模型下，獲得了較高的重構精度。

在對非自由聲場中目標聲源輻射重構的研究中，所重構的聲學量多為聲壓標量，而對介質粒子速度矢量的重構則相對較少。相對于聲壓場，粒子速度場包含了更為豐富的聲場信息。然而，粒子速度重構的傳遞矩陣的病態性也更大[19]。因此，對粒子速度的重構相比于對聲壓的重構更具有挑戰性。Jacobsen等[8,11]以統計最優近場聲全息技術為基礎，對非自由聲場中目標聲源的粒子速度場進行了重構，并對比了以雙層聲壓測量面、雙層粒子速度測量面和單層聲壓-粒子速度聯合測量面作為測量前端時的重構精度。Langrenne等[15]提出了基于逆邊界元法的聲波分離方法，對置于剛性反射邊界附近的目標聲源的粒子速度場進行了重構。Hu等[6,9-10,12]基于等效源法，對目標聲源的粒子速度場進行了重構，并對比了雙層聲壓測量面和雙層粒子速度測量面得到的重構結果[9-10]。基于傅里葉聲學法，Hu等[4]對非自由聲場中平面聲源輻射的粒子速度場進行了重構。

基于球面波函數疊加的近場聲全息方法所使用的全息測量面可以為不規則的、非封閉的幾何形狀，相比于傅里葉聲學法、統計最優法和逆邊界元法，其實施更為靈活[1,19]。另外，隨著P-U探頭[20]技術的不斷發展，在實施全息測量時，直接獲取聲場中的粒子速度變得容易。因此，本文在基于球面波函數疊加的近場聲全息方法的基礎上，輔以單層的粒子速度測量面作為前端，對非自由聲場中目標聲源輻射的粒子速度場進行重構。

本文的第1節介紹粒子速度重構的數學模型；第2節通過數值仿真對所提方法加以驗證；第3節對所提方法進行消聲室內的實驗驗證；第4節是對全文的總結。

1 數學建模

1.1 自由聲場中粒子速度的建模

自由聲場中任意場點處的聲壓可表述為有限項的球面波函數的疊加[19]。當聲場為穩態時，忽略時間變量t的相關項e-iωt，其中：i=，ω為聲波角頻率，場點x的聲壓p(x;ω)的表達式為

其中：ψj(x;ω)為球面波基函數，cj(ω)為基函數系數，j為基函數項序數，J為基函數總項數。使用球面坐標(r,θ,φ)，ψj(x;ω)可表示為[19]

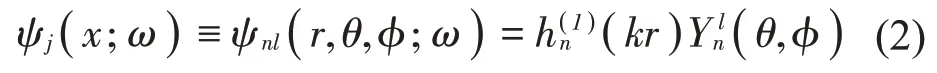
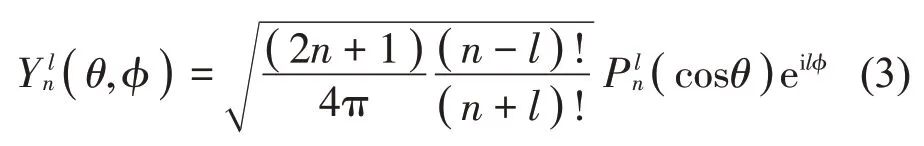
在自由聲場中，場點x處的聲壓p(x;ω)與粒子速度v(x;ω)通過歐拉方程建立聯系：

其中：Δ為梯度算子。將式(4)代入式(1)中，可得到場點x處的，在單位法向矢量n方向的粒子速度分量：

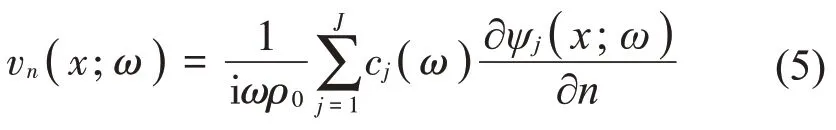
若在聲場中布置傳感器采集一組場點的聲壓或法向粒子速度，則由式(1)和式(5)分別可得：

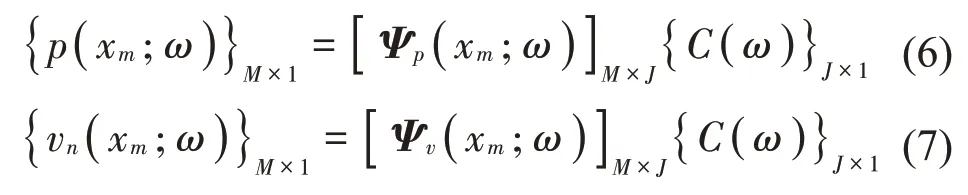
其中：C(ω)為基函數系數列向量，m=1,…,M，M為采樣點數，聲壓展開矩陣Ψp(xm;ω)與粒子速度展開矩陣Ψv(xm;ω)滿足關系式：

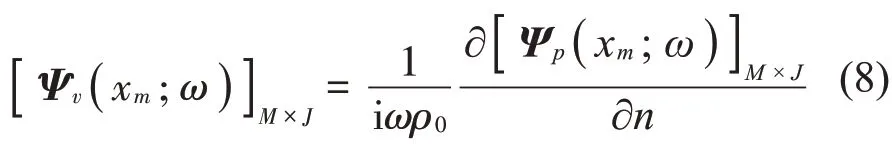
使用包含M個粒子速度測點的全息測量面采集測量面法向的粒子速度分量，通過對式(7)求逆，可求出基函數系數向量：

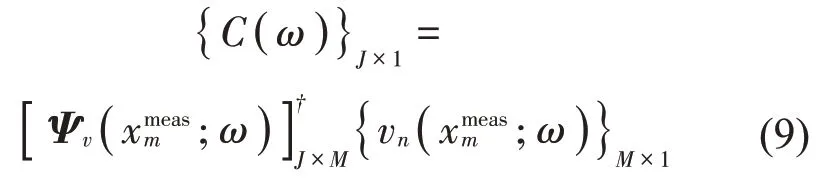
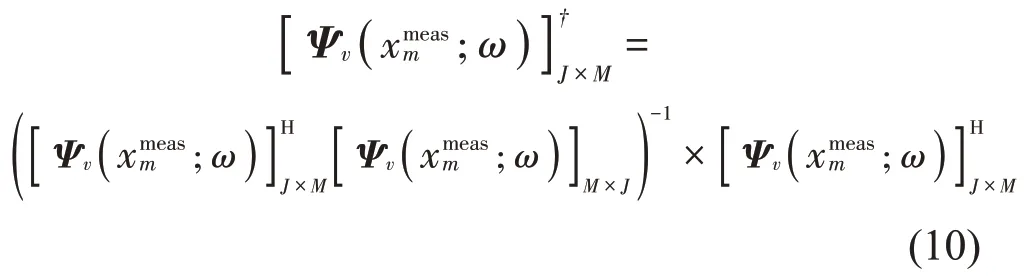
其中：上標H表示共軛轉置。當基函數系數C(ω)求得之后，在聲源表面或空間的場點處的法向粒子速度可由下式重構得到：

其中：s=1,…,S，S為重構點數為重構點處的法向粒子速度的展開矩陣。

1.2 非自由聲場中粒子速度的重構

如圖1所示，當粒子速度測量面另一側存在干擾聲源時，第1.1節中所述的方法不再適用于目標聲源的輻射粒子速度場的重構，因為，測量面所處的聲場為非自由聲場。

圖1 目標聲源和干擾聲源輻射的非自由聲場

以目標聲源的幾何中心O1和干擾聲源的幾何中心O2為原點建立局部坐標系，在第m個測點處，目標聲源和干擾聲源的法向粒子速度的貢獻可分別表示為

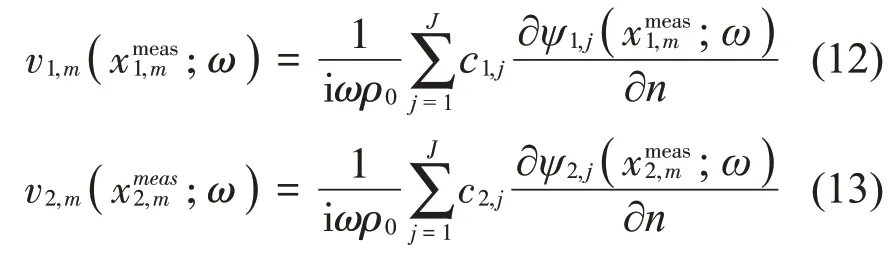
其中：

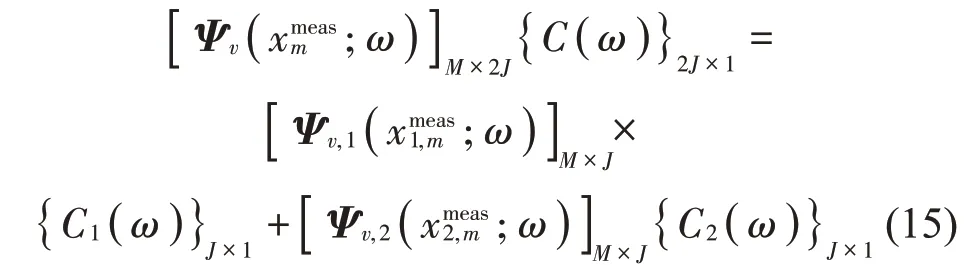
其中：上標T表示向量的轉置。式(15)右邊的兩疊加項的物理意義分別為源于坐標原點O1和O2的外行波。求解式(14)，可得系數向量為

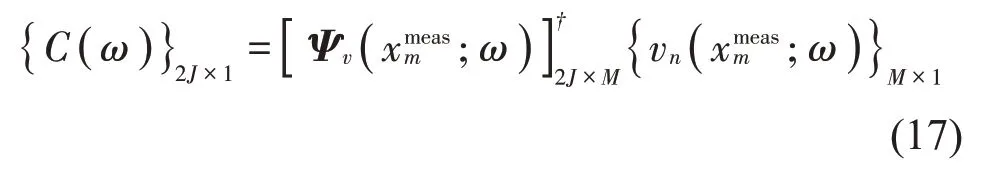
在求解系數向量之前，需要確定最優展開項數Jopt。將重構的粒子速度與采集的粒子速度進行對比，計算出相對誤差的2-范數，遍歷不同的展開項數重復上述過程，將最小誤差2-范數的對應的展開項數定為最優展開項數Jopt。在數學上，最優項數選取準則可表示為[21]

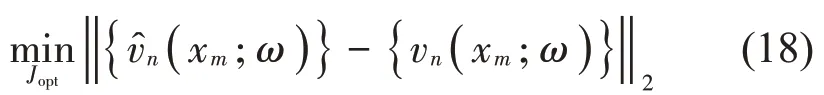
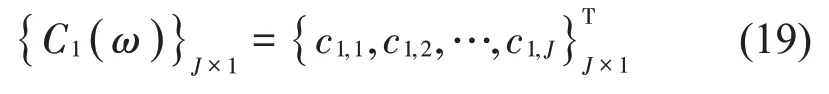
再結合式(11)即可重構出目標聲源輻射的粒子速度場。

2 數值仿真

在本節中，選取脈動球、剛性擺動球和點激勵簡支板，這3類輻射粒子速度場具有解析解的聲源，對所提方法進行仿真驗證。空氣密度和聲速分別設為1.29kg/m3和340m/s。為了對重構精度量化評估，定義重構面上的相對重構誤差為[16]

2.1 脈動球和剛性擺動球輻射的非自由聲場

圖2所示為目標聲源、干擾聲源和粒子速度傳感器陣列組成的仿真聲場。定義全局坐標系Oxyz以描述兩聲源和陣列之間的相對位置關系，O1和O2分別為兩組球面波函數的局部坐標原點，各自位于兩個聲源的幾何中心。使用脈動球和剛性擺動球分別作為目標聲源和干擾聲源。脈動球半徑為0.05m，球心坐標為(0.06m,0m,0m)，球面質點徑向振動速度為0.011m/s。剛性擺動球聲源半徑為0.05m，球心坐標為(0.06m,0m,0.4m)，球體沿z軸方向擺動速度為0.016m/s。平面粒子速度傳感器陣列的孔徑為0.2m×0.2m，其上包含36個測點，相鄰測點間距為0.04m，使得在頻率f=1500Hz時，一個聲波波長包含6個測點；陣列面幾何中心位于z軸，與x-y平面平行，兩者距離為0.1m。為了便于描述重構結果，對36個粒子速度測點編號，如圖3所示。

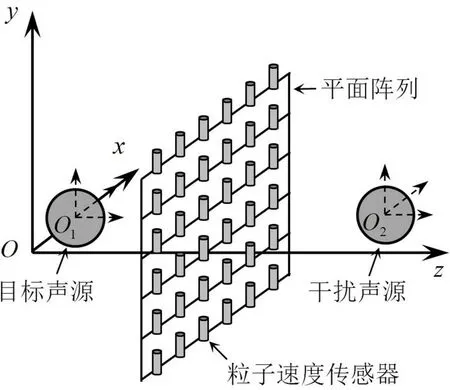
圖2 脈動球、剛性擺動球以及粒子速度傳感器陣列組成的仿真聲場模型

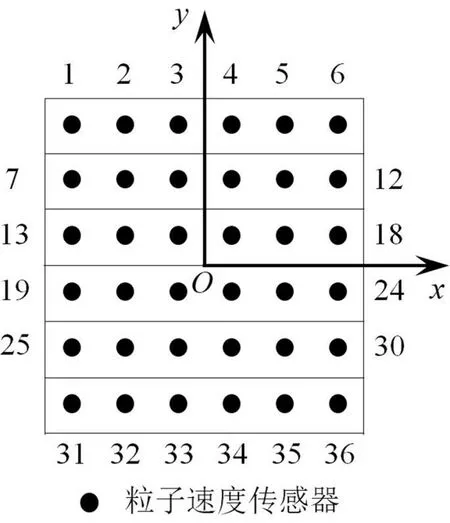
圖3 陣列上傳感器的分布和編號規則

其中，第1號測點坐標為(-0.1m,0.1m,0.1m)，第36號測點坐標為(0.1m,-0.1m,0.1m)。需要說明的是，平面陣列并非本方法的最優陣列形狀。與目標聲源幾何結構共形或者近似共形的陣列更有利于均勻地采集目標聲源的聲場信息，得到更高的對目標聲源輻射粒子速度的重構精度[17]。然而，在仿真和實驗中，均使用平面陣列采集粒子速度信息，目的在于檢驗所提方法對陣列拓撲結構的魯棒性。對陣列的測量值施加信噪比為30 dB的高斯白噪聲，以模擬測量誤差的影響。

使用本文所提方法重構出脈動球輻射在陣列各測點處的法向粒子速度。結果顯示，最優展開項數為Jopt=3，相對重構誤差為ε=2.54%。圖4(a)和圖4(b)給出了各測點處的法向粒子速度幅值和相位的分布，包括兩聲源輻射的疊加值、目標聲源輻射的重構值和理論值。從圖中可知，由于受到干擾的剛性擺動球輻射的影響，無論是幅值還是相位，兩聲源的疊加值相對于理論值均存在一定的偏差。使用本文所提出的粒子速度重構方法后，重構值與理論值能夠很好地吻合。結果表明，該方法能以很高的精度抑制剛性擺動球輻射的影響，重構出脈動球聲源輻射的粒子速度場。

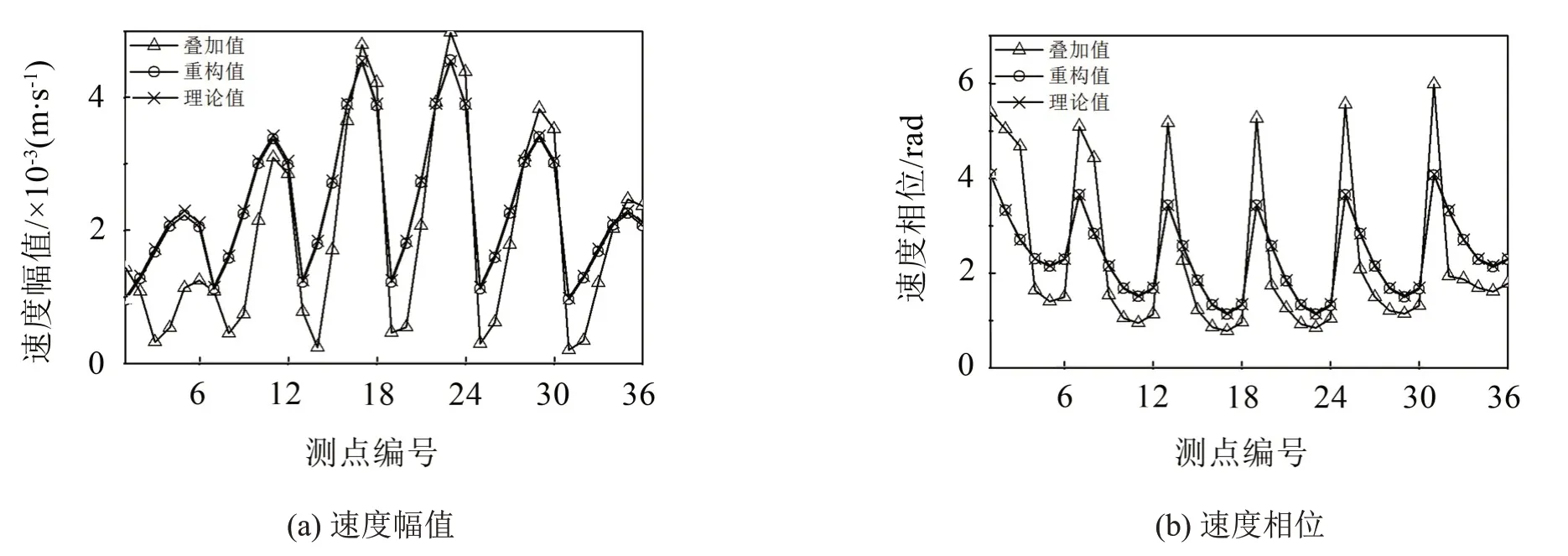
圖4 粒子速度在陣列各測點處的分布曲線，包含兩聲源輻射疊加值、脈動球輻射的重構值和理論值

2.2 剛性擺動球和點激勵簡支板輻射的非自由聲場

在上一算例中，目標聲源和干擾聲源均為理想的球形聲源，使用低階的球面波函數即可對其輻射聲場精確描述，因而獲得很高的重構精度。在本算例中，選用剛性擺動球作為目標聲源，選用在工程應用中更為常見的板聲源作為干擾聲源，對該方法進行進一步驗證。

仿真聲場模型如圖5所示。剛性擺動球半徑為0.04m，沿z軸方向的擺動速度為0.05m/s，球心O1，即描述其輻射聲場的球面波函數的局部坐標系原點的全局坐標為(0.08m,0m,0m)。方形簡支板的邊長為0.16m，板的振動表面與x-y平面平行，其幾何中心位于(0m,0m,0.5m)。板的其它參數為：楊氏模量，2.06×1011Pa；泊松比，0.3；厚度，0.001m；密度，7 850kg/m3。對板施加幅值為25N的簡諧激勵，施力點坐標為(0.05m,0m,0.5m)，并假定在板所在的平面上，其外部區域為剛性障板，即表面振動速度為零，此時，板表面的速度分布可由模態疊加法計算得到。在得到表面速度分布之后，板輻射粒子速度場可由瑞利第一積分聯同歐拉方程計算得到。在本算例中，選取簡支板振動的前25階模態計算其表面速度分布。根據文獻[21]，將描述板輻射聲場的球面波函數的局部坐標原點O2設置在(0m,0m,0.58m)處。平面粒子速度傳感器陣列的孔徑、測點數、相鄰測點間距以及測點坐標等參數與上一算例相同。對陣列的測量值施加信噪比為30dB的高斯白噪聲。

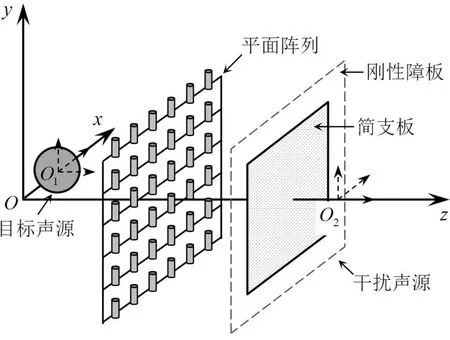
圖5 剛性擺動球、簡支板以及粒子速度傳感器陣列組成的仿真聲場模型

使用本文所提方法重構出剛性擺動球聲源在陣列各測點處的法向粒子速度。結果顯示，最優展開項數為Jopt=12，相對重構誤差為ε=14.67%。圖6(a)和圖6(b)給出了各測點處的法向粒子速度幅值和相位的分布，包括兩聲源輻射的疊加值、目標聲源輻射的重構值和理論值。

從圖6(a)中可知，由于受到板聲源的輻射的影響，在大多數測點處，兩聲源疊加的幅值相對于理論值均明顯偏大，并且，兩者在各測點分布趨勢明顯不同。使用本文所提出粒子速度重構方法后，重構幅值與理論幅值能夠較好地吻合，誤差較大的測點多分布在陣列邊緣的測點處，因為在使用球面波函數描述板聲源聲場時，對陣列中心附近場點的描述精度要高于對邊緣場點的描述精度。在圖6(b)所示的速度相位分布中，也能觀察到類似的現象。結果表明，該方法能以一定的精度抑制板輻射的影響，重構出剛性擺動球輻射的粒子速度場。

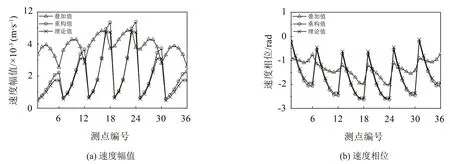
圖6 粒子速度在陣列各測點處的分布曲線，包含兩聲源輻射疊加值、剛性擺動球輻射的重構值和理論值

3 實驗驗證

在本底噪聲低于18 dB(A)的全消聲室中，對本文所提方法進行了實驗驗證，主要的實驗設備布置如圖7所示。在實驗中，使用兩個直徑約為0.05m的同型號揚聲器作為目標聲源和干擾聲源，聲源紙盆中心坐標分別為(0m,0m,0m)和(0m,0m,0.2m)。使用的粒子速度采集前端為Microflown公司生產的手持式P-U探頭陣列。該陣列為平面陣列，孔徑為0.225m×0.150m，其上均勻分布12個探頭，測點間距為0.075m。陣列面與x-y平面平行，距離為0.05m。對12個測點進行編號，如圖8所示。

圖7 主要實驗設備的布置

圖8 陣列上P-U探頭的分布和編號規則

在實驗數據采集過程中，首先同時驅動兩個揚聲器以相同頻率發聲，使用P-U探頭陣列采集聲場粒子速度，得到粒子速度的疊加值；然后，關閉干擾聲源，在相同參數下驅動目標聲源發聲，采集得到目標聲源輻射的理論值。設置第9號測點處采得的聲壓信號作為參考信號。12個通道采集的粒子速度信號與參考信號進行互功率譜計算，得到各測點法向粒子速度的相位信息；12個通道采集的粒子速度信號進行自功率譜計算，得到各自的幅值信息。然后，將各測點處的法向粒子速度的頻域值輸入重構算法，對測量面上各測點處的粒子速度進行重構，得到目標聲源輻射的重構值。

給出頻率為f=1500Hz時的重構結果。當f=1 500Hz時，最優展開項數為Jopt=11，相對重構誤差為ε=8.67%。圖9(a)和圖9(b)給出了各測點處的法向粒子速度幅值和相位的分布，包括兩聲源輻射的疊加值、目標揚聲器聲源輻射的重構值和理論值。觀察圖9發現，由于受到干擾揚聲器輻射的影響，兩聲源的疊加的速度分布遠遠偏離于目標揚聲器輻射的理論分布。使用本文所提出的粒子速度重構方法后，重構值與理論值能夠較好地吻合，這說明干擾揚聲器聲源的輻射所造成的影響被較好地抑制。實驗結果驗證了本文所提方法在存在干擾聲源輻射影響的情況下，對目標聲源輻射粒子速度場的重構效果。

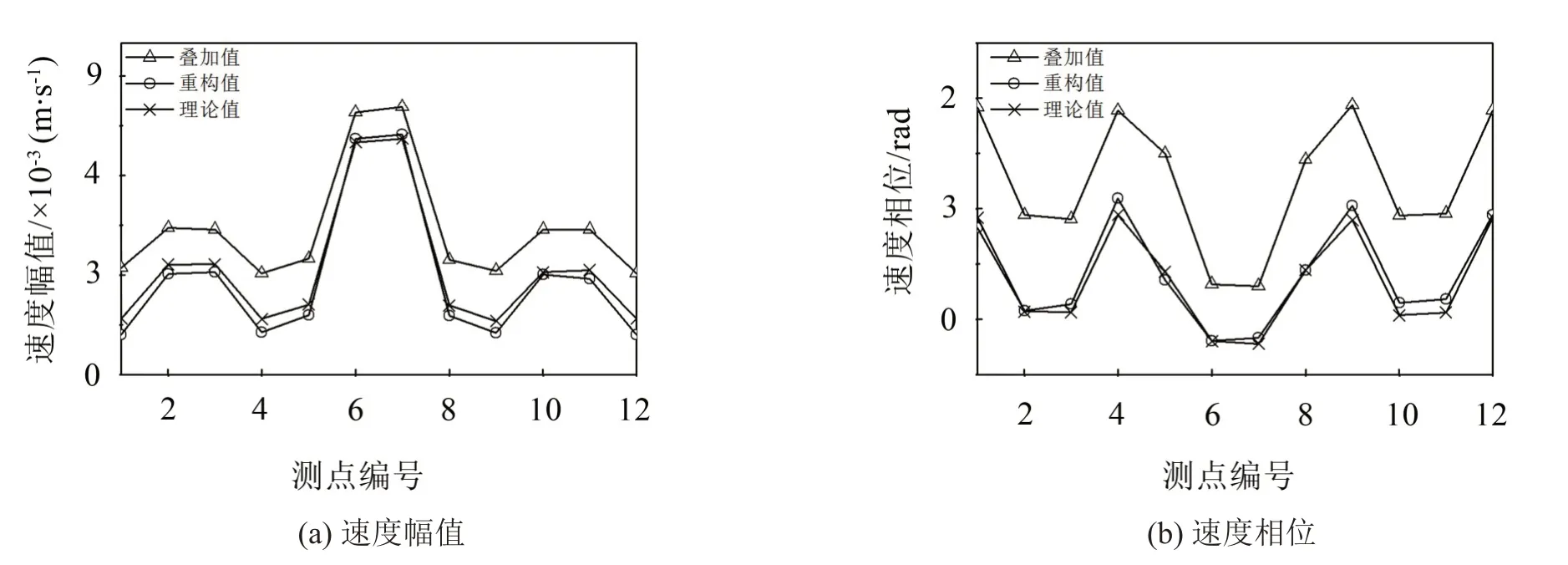
圖9 粒子速度在陣列各測點處的分布曲線，包含兩揚聲器輻射疊加值、目標揚聲器輻射的重構值和理論值

將實驗的重構誤差與兩個仿真算例的重構誤差進行對比分析。第2.1節中以剛性擺動球作為干擾聲源時的重構誤差最低，第2.2節中以點激勵簡支板作為干擾聲源時的重構誤差最高，實驗所得的重構誤差介于兩者之間。這是因為，在所建的聲場模型中，以兩組球面波擴展函數分別描述目標聲源和干擾聲源的輻射粒子速度場，從而，該模型對球形聲源輻射粒子速度場的描述精度高于對板形聲源的描述精度。所以，在仿真算例中，以球形聲源作為干擾聲源時的重構精度遠高于以板形聲源作為干擾聲源時的重構精度。對于實驗而言，一方面，由于揚聲器聲源輻射聲場接近于雙極子聲場，球面波擴展函數對其輻射聲場的描述精度高于對板形聲源的描述精度，使得重構誤差比第2.2節的重構誤差為低；另一方面，實驗的聲場環境較仿真而言更為復雜，使得重構誤差比第2.1節中以理想的球形聲源作為干擾聲源時的重構誤差為高。另外，由于實驗所用到的P-U探頭陣列為商業化產品，其測點間距、測點個數和測量孔徑等參數為固定值，且并非該聲場條件下的最優化陣列參數。如果適當減小測點間距、增大測點數目，可以更為充分地采集聲場信息，實驗有望獲得更高的對目標聲源輻射粒子速度的重構精度。

4 結語

本文提出了一種基于單層粒子速度測量面作為測量前端的非自由聲場中目標聲源輻射粒子速度場的重構方法。該方法使用兩組球面波擴展函數分別對目標聲源和干擾聲源的輻射粒子速度場進行建模，以兩組基函數的線性疊加來匹配全息測量面上測得的粒子速度場，通過求解兩組基函數的系數，重構出目標聲源單獨輻射的粒子速度場。

在數值仿真中，以球形聲源和板形聲源作為干擾聲源，對球形目標聲源的輻射粒子速度場進行了重構，結果表明，所提方法均能以較高的精度重構出目標聲源的輻射粒子速度場，其中，當干擾聲源為球形聲源時的重構精度高于當干擾聲源為板形聲源時的重構精度。在消聲室內，使用兩個揚聲器聲源作為目標聲源和干擾聲源，以較好的精度重構出目標揚聲器單獨輻射的粒子速度場，對所提方法給予了實驗驗證。該方法為實際復雜聲場環境中，目標聲源的輻射粒子速度場的重構提供了解決方案。