風機散熱電機支撐系統模態分析與結構優化

邊蘊宇，續秀忠，霍明莉，顧憲成

（1.上海海事大學 物流工程學院，上海 201306；2.敏泰液壓技術有限公司，上海 201299）

出于我國對綠色能源的大力推廣，風力發電在新能源中所占的比重日益增大[1]。風力發電機存在溫升快、散熱難的問題，制約著風力發電機的發展。作為風力發電機的重要部件，散熱系統能有效地對發電機進行快速冷卻，避免材料損耗，影響使用壽命，并有效減少事故的發生。現行的散熱系統設計主要采用空冷和液冷兩種方式，其中空冷需要安裝散熱電機使冷空氣作用于發電機冷卻風道或者電機關鍵部件進行對流冷卻[2]。散熱系統的電機支撐系統出現異常振動，不僅會產生噪聲，還可能對電機結構造成損傷，影響電機的使用壽命，進而對整個機組造成影響[3]。

國內外對于電機系統的振動控制技術已經有了一定的研究成果。在國外，Bogh等[4]研究了引起電機振動的物理方面的原因并提出了減小振動的方法；Gu等[5]通過仿真與實驗相結合的方法計算了電機的固有頻率，并驗證了模型的有效性；Liang等[6]利用Labview建立了試驗系統，采集電機振動信號進行分析，對電機振動進行了檢測與分析。在國內，張俊林[7]用有限元法，對牽引電機的靜、動態特性和疲勞壽命進行了分析，并通過實驗驗證，對電機結構做出了改進；張宇[8]綜合考慮了電磁力和外界荷載，利用有限元法進行仿真，對電機定子、機殼、支座等結構進行了優化設計；王強等[9]從機械和電磁兩方面進行研究，得出了籠型三相異步電動機的振動故障特征和預防措施。然而，多數的研究更加側重于電機運轉時產生的電磁場對電機振動造成的影響，而忽略了電機系統本身物理特性對振動造成的影響。

因此，本文對散熱系統的電機支撐系統進行了動力學分析和有限元建模，對模型的簡化和約束做出了處理，并通過實驗進行驗證。該研究提供了一種減小電機支撐系統振動的方法，并對支撐系統的設計提供了動力學方面的借鑒。

1 電機支撐系統理論模型

由牛頓第二定律建立電機系統的振動微分方程[10]為

為了得到電機的固有頻率，忽略阻尼的影響，并且忽略外部激勵，即在f(t)=0的情況下，得到系統自由振動的動力微分方程：

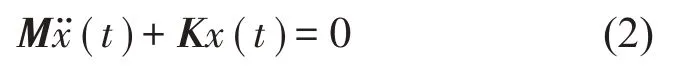
運用高等數學的方法解該常系數微分方程，設其特解為x=φejωt，將其代入上式，可得：

該方程有非零解的充要條件是其系數行列式為零，即：

由此得到：

2 電機支撐系統振動試驗

為了找出支撐系統異常振動的原因，在現場進行了振動測試與分析。現場測試的流程圖如圖1所示。

圖1 現場測試的流程

2.1 實驗設備

測試硬件主要包括FD23550Y系列散熱器連接總成一套、加速度傳感器8個、東方所采集儀一套、計算機等。數據采集與分析軟件采用DASP V11，采集儀為東方所8通道信號采集分析儀。

2.2 測試方案

采樣頻率設置為1 024 Hz[11]。現場測試如圖2所示。在現場發現，電機的水平方向振動明顯，鉛垂方向沒有明顯的振動。測點應該布置在對結構振動較為敏感的位置，同時也應該能夠對結構的整體狀況進行清晰的觀測，所以電機和支架均有布置測點。由于電機輸出軸無法布置測點，所以支架測點設在靠近電機輸出軸位置。具體測點分布1～3為電機上部斷面圓周方向的3個點；4～6為電機下部斷面圓周方向的3個點、7～8為支撐板水平側向靠近電機輸出軸位置2個測試點。測點布置如圖3所示。

圖2 現場測試

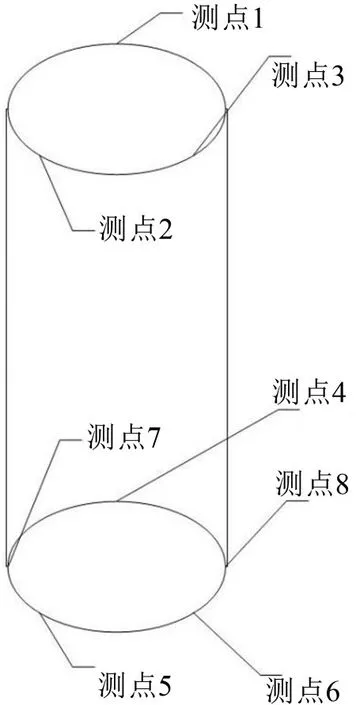
圖3 測點布置圖

加速度傳感器采用膠接的方式布置在測點上，傳感器線纜則盡可能與電機自身的線纜固定在一起，以減小環境噪聲的干擾。

每組采用8個通道采集數據，并將數據導入到DASP V11軟件進行自譜分析（FFT變換）。在自譜圖中，采用峰值拾取法讀出振動測試結果，第一個波峰代表的就是結構的1階模態，讀出波峰的橫坐標即為結構的1階頻率，2階、3階頻率以此類推，得到電機系統的振動測試結果。

2.3 實驗結果

測試分3組進行：

(1)采用工作狀態激勵，電機低速運行（轉速720 r/min）；

(2)采用工作狀態激勵，電機高速運行（轉速1 440 r/min）；

(3)采用錘擊法進行激勵，電機處于未運行狀態。

測得的頻率結果如表1。

表1 實驗測得的頻率結果

測得外部激勵頻率為1階12 Hz，2階24 Hz，電機支撐系統固有頻率為1階13 Hz，2階25 Hz，電機支撐系統的固有頻率和外部激勵頻率過于接近，電機的異常振動是由于共振引起的。

3 電機支撐系統有限元仿真

3.1 支撐系統建模

散熱電機型號為AKD132M型三相異步電動機，由外殼、定子、支架、轉子、線圈等組成，電機支撐系統如圖4所示。

圖4 電機支撐系統

由于轉子、線圈等質量占比不大，而且建模比較復雜，所以在建模時，參照文獻[8]的處理，未給出實體模型，只考慮其質量的影響。對于一些微小且復雜的結構，如連接結構、凸臺等也做簡化處理。在Solidworks 2014中進行建模，對電機的復雜外殼進行了簡化，用一個空心的圓柱代替，定子的槽型為平行槽。對于電機定子，由于在實際制作中是用硅鋼片堆疊而成，其上纏繞線圈等各種零部件，零部件之間具有復雜的連接屬性，所以在仿真中無法準確得知材料的參數。參照文獻[8]對材料參數的處理，將其定義為各向異性材料，結合前人的經驗并利用模型修正法[12]，對仿真模型的材料參數確定如表2。按照表2將不同的材料參數分別賦予支架、外殼和定子。

表2 仿真模型的材料參數

為了使計算結果精確，限制體單元網格尺寸為20 mm，并對螺栓孔處的網格進行了細化，細化系數為1。為了模擬實際安裝情況，給支座的8個螺栓孔添加固定約束，引入重力因素，Z方向加速度為9 806.6 mm/s2，用BEAM單元模擬螺栓連接來連接電機和支架。

3.2 模態分析

將建立的模型導入modal模塊進行模態分析，得到電機的前3階固有頻率及其對應的振型如圖5所示。

圖5 電機有限元分析前3階振型

3.3 支架結構優化

利用有限元仿真來對支架結構進行優化。電機支架厚度為6 mm，翼緣板高度為40 mm，仿真將通過調整支架的厚度和翼緣板高度來進行。

支架翼緣板高度以30 mm為初始值，以5 mm為梯度，增加至50 mm；支架的厚度以6 mm為初值，以2 mm為梯度，增加至14 mm。10組仿真模型在有限元軟件ANSYS workbench中進行求解，所得前3階頻率結果如表3，圖6為仿真結果折線圖。

由表3和圖6可以得出：增加支架翼緣板的高度和增加支架的厚度，固有頻率都有不同程度的增加。仿真結果表明通過調整支架尺寸從而對電機結構的固有頻率進行調整是可行的。由圖6可以看出：增加支架厚度對電機系統固有頻率的調整效果要優于增加支架翼緣板高度，但是兩種方案都是可行的。

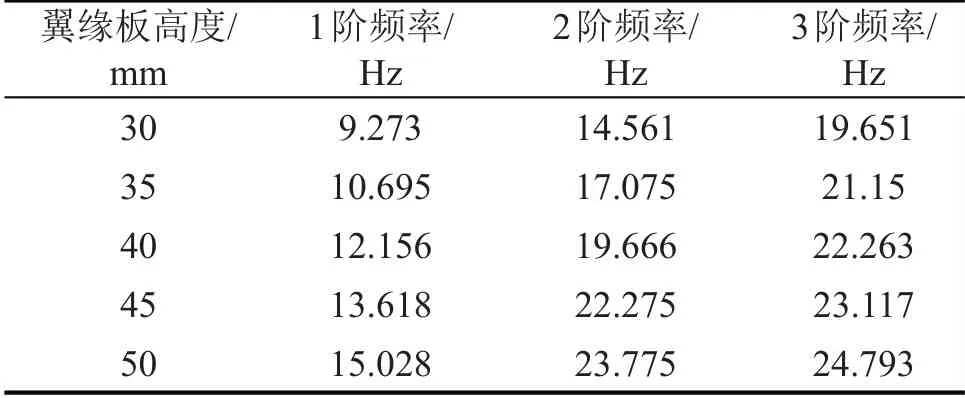
表3 -a調整翼緣板高度的前3階頻率

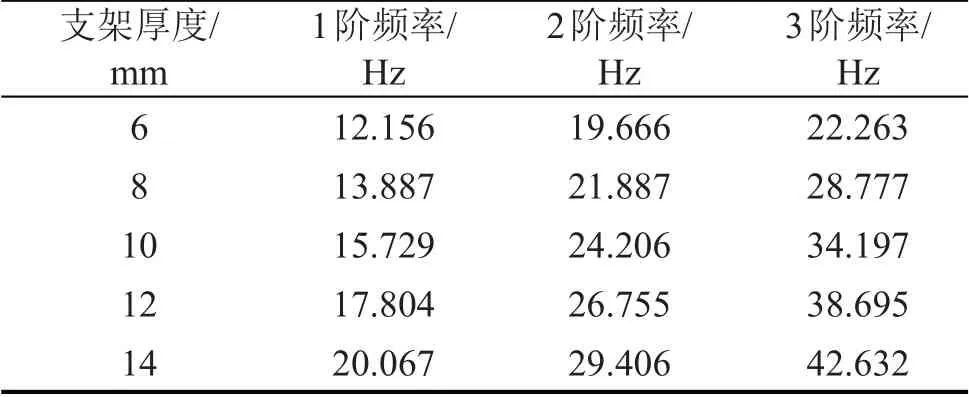
表3 -b調整支架厚度的前3階頻率

減小翼緣板高度，對支架結構造成了削弱，可能導致支架的強度剛度下降，產生結構損傷；過度增加支架的厚度或增加翼緣板高度會使結構的3階頻率增大，但是會造成材料的浪費和裝配的不便。

4 優化結果實驗驗證

為了對支撐系統結構優化的效果進行驗證，在現場制作了翼緣板厚度為50 mm的支架，并安裝在電機上，對新的支撐系統進行模態測試。測試方法與章節2相同，模態測試結果如表4所示。對未加厚翼緣板電機系統與加厚翼緣板電機系統的低速運行過程進行測試所得的自譜分析圖如圖7所示。由圖7可以看到：支架翼緣板加厚后，電機振動頻率的幅值明顯變小。

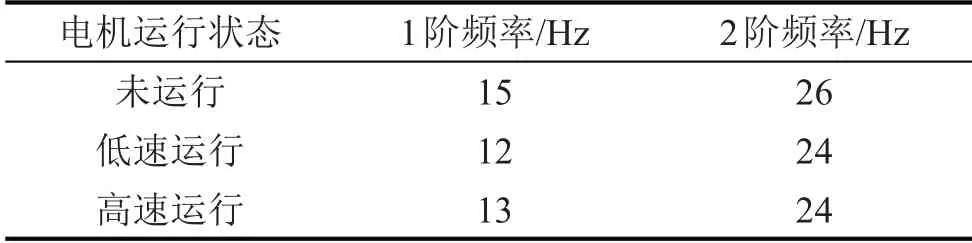
表4 實驗測得的頻率結果

由表4可以得出：隨著翼緣板厚度的增加，整個電機系統的各階固有頻率增加，1階由13 Hz增加到15 Hz，2階由25 Hz增加到26 Hz。外部激勵頻率為12 Hz、24 Hz，處于共振帶寬范圍之外[13]，可以有效避免共振的發生，減小電機結構的振動。

本文提出的方法可以對電機系統的固有頻率進行有效的調整。利用該方法，工程實際中可以通過調整翼緣板厚度來調整電機的固有頻率，從而避開共振區，減小電機的振動。

圖6 仿真結果折線圖

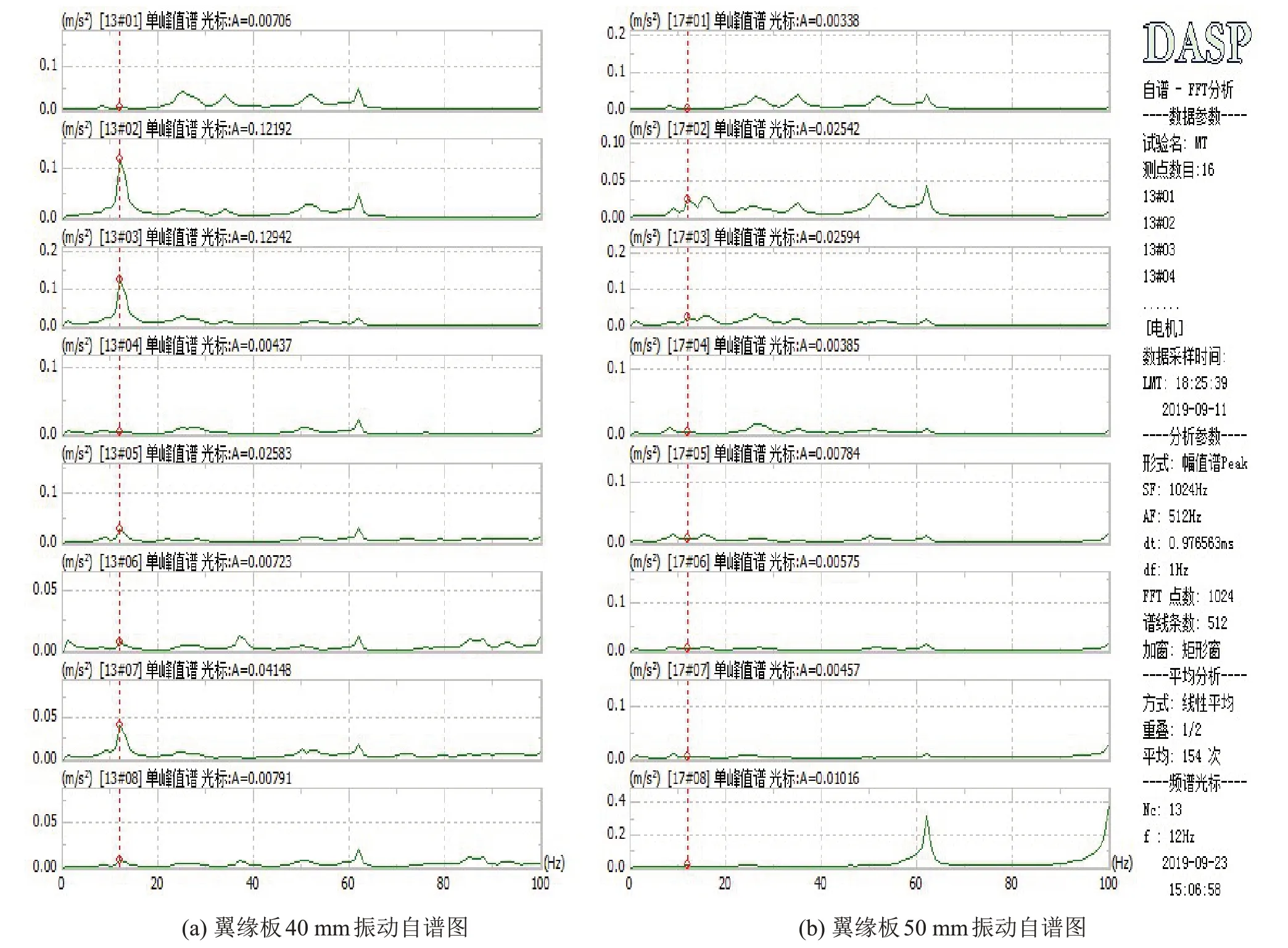
圖7 電機低速運行狀態下翼緣板優化前后結構振動自譜圖

5 結語

對于電機支撐系統異常振動的控制，有別于傳統的電磁場分析，筆者從電機本身的結構出發，通過模態測試得到異常振動是由共振引起的，并用有限元方法進行建模和結構優化，給出了通過調整支架尺寸來調整頻率的方法，之后的優化結構模態試驗證明了該方法是可行的、有效的。由于本方法的簡便易行，可以將本方法應用于工程實際和電機系統的動態設計中，對于減小電機支撐系統振動提供了一種可行易操作的方法。

在工程實際中，可以先進行模態試驗得出電機的固有頻率和激勵頻率，若兩者接近，則可以增加電機支架翼緣板的高度來調節電機的固有頻率。

本文采用的方法取得了較為理想的結果，對電機的建模仿真和結構優化提供了一定的借鑒，對于工程結構的仿真與優化提供了參考，該方法也可用于電機系統的動態設計。