基于鍵相信號截取的整周期采樣方法

張燁

（西安紫星電子科技有限公司，陜西西安，710072）

0 引言

在進行轉子動平衡分析時，需要準確測量轉子基頻振動信號的幅值A和相位θ。對于采樣序列x(1)、、x(2)、…x(N)，基頻振動的幅值A和相位θ與FFT基頻幅值A1和相位θ1存在關系：A= 2A1/N,θ=θ1，其中N為采樣點數（滿足N= 2n，n為正整數的條件），因此一般都是通過對振動信號進行FFT來計算A和θ。根據數字信號處理理論可知，對N點采樣序列進行傅立葉變換后，如果序列為非整周期截斷，則會因為譜泄漏造成FFT幅值和相位的失真[1]，從而不能準確得到基頻振動的幅值和相位。解決這個問題的有效辦法就是采用整周期采樣。

常用的整周期采樣方法是通過數字鎖相環[2]來實現的。其基本原理是在鎖相環和計數器的共同配合下，鍵相信號在鎖相環輸入端產生一個脈沖信號，輸出端就會輸出N個脈沖信號觸發A/D轉換，實現N倍頻的整周期采樣。由于當前采樣脈沖輸出頻率是根據上一周期得出的，如果轉速波動引起周期變化較大，那么這種方法也并不能真正實現整周期采樣。此外，鎖相環的時基分辨率對于采樣也有較大影響[3]。因此該方法適用于轉速較低、波動較小的場合。某型航空發動機轉速高、速度波動較大，不適宜采用鎖相環來進行整周期采樣。針對這個情況，本文利用軟件方法，通過鍵相信號作為振動信號整周期截取的依據[4]，實現了整周期采樣。

所謂鍵相信號，是由安裝在轉軸上的渦流傳感器在轉軸每轉一圈時產生的脈沖，它的每一個脈沖唯一對應于轉子周向一固定點，可以用于確定轉子上其它徑向振動量信號的相位，該脈沖能為振動信號提供轉軸每轉一圈時的參考標準。由鍵相信號產生采樣觸發信號，即作為振動信號整周期采集的外觸發脈沖，同時一通過兩個鍵相信號之間的時間間隔來換算轉換記錄實時轉速值，鍵相信號也可以用于確定轉子上其它徑向振動量信號的相位。

根據頻譜分析的要求，必須對振動量進行整周期采樣以避免傅立葉離散變換時的泄漏效應與柵欄效應。因此，要求振動量采樣的觸發脈沖頻率必須能跟隨機組轉速的變化而相應變化。另外轉速自身作為進行振動分析的一個極其重要的參數,也要求能夠準確及時地獲得。這些問題，都可通過對轉子的鍵相信號進行實時處理而解決。

鍵相信號可以用光電式、渦流式、磁電式傳感器對轉子上的標志區或鍵槽進行檢測來拾取。通常我們用渦流式傳感器來檢測鍵相信號，要得到好的信號,關鍵是鍵槽的形狀、尺寸及在轉子上開槽的位置以及傳感器安裝的位置，鍵槽及傳感器的安裝。

旋轉機械振動測試中，一般是通過在旋轉機械的軸上開一鍵槽，然后裝上振動信號傳感器，便可以測得原始鍵相信號，該鍵相信號是用來對旋轉機械進行測速與振動信號整周期采樣的基準信號。

1 依據鍵相信號的整周期截取

■1.1 整周期截取原理

在旋轉機械動平衡時，一般都需要采用鍵相信號作為計算相位的參考基準。在發動機轉子前端的整流罩上貼上反光貼片，光電傳感器對準整流罩，當反光貼片轉到光電傳感器位置時，產生一個鍵相脈沖。兩個鍵相脈沖之間轉子必然正好旋轉了一周，兩個鍵相脈沖的時間間隔也必然為信號的周期，因此可以考慮采用鍵相脈沖作為信號整周期截取的依據。

采用固定采樣率連續同時采集若干時間內的鍵相信號和振動信號（這里采集時間長度t至少應該大于1個周期以便截取數據），如圖1所示，兩個鍵相脈沖上升沿之間的時間間隔即為信號周期T，所采集的N個點也必為1個整周期的數據，從而實現了對信號的整周期截取。

圖1 鍵相信號整周期截取原理

由于采用鍵相信號而不是實現設定好的固定點數作為整周期截取的依據，當周期變大時，截取數據點數會相應增多，當周期減小時，截取數據點數會相應減小，始終保證是整周期截取，從而避免了轉速變化的影響。

■1.2 采樣率的確定

由于需要根據兩個鍵相信號的上升沿來確定信號的周期T和實際采樣點數N，能否及時捕捉到鍵相信號的上升沿對于決定能否對信號實現整周期采樣具有重要意義。如果鍵相信號捕捉不及時，則必然引起周期測量誤差，從而造成非整周期截斷。

設信號周期為T，在該周期內的采樣點數為N，采樣間隔時間，則通過采集兩個鍵相脈沖測出的周期誤差將不大于，相對誤差為。本文對信號在不同的整周期截斷相對誤差條件下進行了仿真分析，結果如表1所示。從表2中可以看出當每周期只采集10個點時，幅度誤差達到0.169，相位誤差更是接近了18°，而當每周期采集200個點時，幅度誤差僅為0.0001，相位誤差也不超過1°。可見每周期采樣點數越多，周期測量越準確，越接近于整周期截斷，幅值和相位誤差也越小。

綜合考慮周期的波動和每周期所需的最小采樣點數，則系統的采樣率應該要滿足：

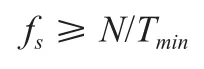
其中Tmin為轉子的最小周期。

表2 采樣點數對分析結果的影響

■1.3 反光貼片的影響

為了保證每個周期內都能捕捉到鍵相信號，還必須滿足采樣時間間隔必須Δt小于鍵相脈沖寬度τ，即T/N＜τ。設反光貼片寬度為w,轉子半徑為r，又有τ/T=w/(2πr)，則結合兩式可以推得w>2πr/N。反光貼片寬度w和轉子半徑r以及采樣點數N必須要滿足w>2πr/N的條件才能保證鍵相信號的采集。

2 鍵相信號誤差分析

鍵相信號的誤差分為頻率誤差和相位誤差。

■2.1 頻率誤差

因時鐘源采用石英晶體振蕩器，時鐘頻率f誤差極小，可認為是0。周期誤差就是兩個鍵相脈沖的時間間隔t和計數器N所代表時間之間的差值。

假定任一時鐘脈沖為時間原點，并把其后的脈沖按順序標記為1,2,3…,兩個相鄰的鍵信號到來的時間分別為t1和t2，緊隨其后的時鐘脈沖分別為n1和n2。

可知：n1=[t1×f]+1；n2=[t2×f]+1

f：時針分期后f：時針分期后f：時針分期后f：時針分期后f：時針分期后頻率f=f?/64

[]表示取整函數，這樣鍵信號周期的絕對誤差：

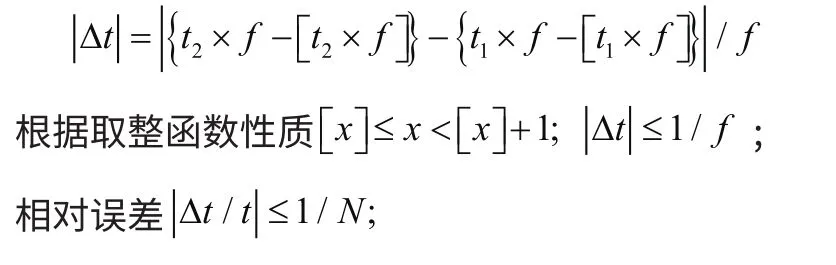
N:計算器的計數值

尤其可得出兩個結論：（1）提高時鐘頻率可減小誤差；（2）當轉子轉速越高測量誤差越小。

■2.2 相位誤差

針對傳感器對軸的徑向位移進行整周期采樣，要求采樣點在軸上均勻，且每一次采樣的位置固定。這樣才能從采樣數據中分離出正確的相位信息。一般用產生鍵相位的槽作為起點，其他的點均分布在軸上。但是由于安裝等各種原因，并不能做到每次采樣的位置固定。采樣點與這些固定點的偏差即為相位誤差。

相位可分為初始誤差和累計誤差兩部分。相位初始誤差為第一個采樣脈沖和鍵相信號之間的相位差，相位積累誤差是由于采樣脈沖和鍵相信號之間的頻率不一致導致的，即：

3 信號的插值重構

采用上述方法得到的采樣點數N往往都不能滿足N= 2n(n為正整數）的條件，不便于進行FFT變換。為此再對采集的N個數據進行插值，重構出能夠直接進行FFT變換的N′個點[5]。

插值[6]的方法有多種，本文采用分段二次插值來重構信號。對于任意一個子區間（對應三個節點tk?1,tk,tk+1），均可構造一個二次插值多項式

其中tk?1≤t≤tk+1。為盡可能減小插值誤差，插值節點的選擇應滿足如下條件：

設在周期T時間內采N個信號x1,x2,x3…xN′'，其對應的采樣時間分別為

t1= 0 ,t2=?t,t3=2 ?t, … ,tN′?1= (N? 1 )?t， 其 中 ?t=T/N為實際的采樣間隔時間。今需要在周期T內插值重構N′個點，則重構的N′個點對應的采樣時間分別為：

=其 中 ?t′=T T/N′為 重 構 的采樣間隔時間。分別以為插值點，根據（1）式即可計算出重構后的信號

4 平均處理

不平衡振動量是與轉速密切相關的，因此利用不同周期內的數據計算出的振動幅度和相位可能都不同。可以將多個周期內的振動幅度和相位分別進行平均，得到平均狀態下的振動幅度和相位以用于指導動平衡。此外，多周期的平均處理也有利于消除隨機噪聲的影響。

5 結論

（1）采用鍵相信號作為整周期截取的依據可以有效避免轉速波動的影響，克服了鎖相環觸發整周期采樣的缺點。

（2）采樣率對于計算結果具有重要影響。采樣率越高，越接近于整周期采樣。此外提高采樣率也有利于減小信號插值重構的誤差。

（3）對多個周期內的幅值和相位進行平均處理以減小隨機干擾。

鍵相信號作為輸入提供給分析診斷系統用于描述轉子的相位，還可提供給偏心測量模塊鍵相信號，用于偏心值的計算，該信號是偏心值計算所必需的。因此鍵相信號的測量在機組保護監測系統中起著相當重要的作用。

實際轉子振動除了基頻分量以外，還可能有多次諧波和次諧波分量。對于以不平衡故障為主的轉子振動而言，其基頻分量占優，諧波分量很小，對整周期截取后譜泄漏的影響很小。當轉子存在其它故障時，諧波分量特別是非整數倍諧波分量較大時，按基頻信號進行整周期截取后，諧波分量并未能被整周期截取，仍然會造成譜泄漏，影響到基頻信號的幅值和相位。因此若存在較大的諧波分量時，可以考慮將其濾掉，以免影響基頻信號的分析結果。