西南電網異步聯網后的負荷預測及頻率波動抑制

羅衛華,余銳,蘭強,吳京馳,王民昆,肖嵩

(1. 國家電網有限公司西南分部,四川 成都 610041；2. 西南交通大學電氣工程學院,四川 成都 611756)

0 引言

電力系統負荷是電力系統穩定分析的重要指標之一,代表系統中所有用電設備瞬時消耗功率的總和。由于電力系統中電能儲存量有限,發電量與負荷量需實時保持供需平衡。2014年12月29日,四川、重慶電網分別脫離華中電網與原西藏電網,組成了西南電網。2019年6月19日,隨著渝鄂直流工程全部投運,西南電網與華中電網脫離交流同步互聯,兩大電網的交流輸電線路全部斷開。依靠背靠背直流輸電工程,西南電網互聯格局由交直流混聯變為直流異步互聯。電網的異步互聯意味著兩端電網旋轉轉動慣量相互分隔,各電網的頻率穩定性能下降,增加了頻率失穩風險。

西南電網異步互聯工程啟用以來,西南電網頻率波動加劇,頻率波動越過動作頻率界限的情況頻發,直流頻率控制(frequency control,FC)裝置動作頻繁。電力系統有功瞬時不平衡將導致頻率波動,由于西南電網的異步運行,有功不平衡對頻率造成的影響將擴大,頻率波動也隨之加劇。因此,有效準確地預測有功出力及制定發電計劃對頻率偏差控制具有重大意義[1—4]。

隨著現代人工智能技術的發展,機器學習方法被逐漸用于電力系統負荷預測[5—8],如經典時間序列預測法、人工神經網絡方法、支持向量回歸(support vector regression,SVR)等。其中時間序列預測法建模簡單、預測速度快,但對于波動性大的負荷,預測精度較低。文獻[9]采用雙鏈馬爾科夫方法預測負荷,達到了預期精度,但預測結果較為固定,無法跟隨預測日的實際工況改變預測趨勢。文獻[10—11]使用長短期記憶網絡(long short term memory,LSTM)進行負荷預測,該方法基于時間序列進行預測,未考慮多方面因素影響,故精度較低。人工神經網絡預測精度高、優化潛力大,但存在一定問題,如收斂速度慢、難以確定網絡結構和易陷入局部最優等。文獻[11]使用反向傳播(back propagation,BP)神經網絡對某電力系統的負荷進行預測,考慮了氣溫對預測結果的影響,取得了一定效果。文獻[12]所述的雙層隨機森林算法也取得了較好的效果。通常SVR算法只能進行單步預測,對于存在大量雜散干擾的數據,預測誤差較大且預測效果滯后[13]。文獻[14]使用基于氣象綜合因素指數和關聯分析加權的最小二乘支持向量機(least squares support vector machine,LSSVM)算法,建立組合預測模型,氣象綜合指數僅表達了氣象對人體的影響程度,無法客觀反映氣象對負荷的影響程度。

為提高負荷預測精度并彌補上述算法的缺陷,文中結合BP神經網絡與SVR各自的優點,提出一種新型混合算法模型。使用預測精度較高的BP神經網絡對系統負荷水平進行預測,使用不易陷入局部最優的SVR預測最終負荷值。其中,BP神經網絡利用訓練集的氣象數據預測當日最大負荷,確定當日負荷水平。基于所得負荷水平,使用當日一段已知的負荷數據確定訓練集權重并訓練SVR模型,進而預測當日剩余時間的負荷曲線。該混合算法模型每隔一段時間根據最新的已知負荷重新訓練模型,實現滾動預測,可適應突發工況。為了應對西南電網異步互聯后的頻率問題,使用BPA仿真將預測的負荷跟蹤系統的有功出力,結果表明預測方法相較于未考慮負荷分布特性的傳統預測方法,頻率偏移抑制效果更佳。文中所提模型及方法對未來電網發電計劃制定以及電力系統頻率穩定性提升具有重要意義。

1 西南電網異步運行現存頻率問題分析

西南電網異步運行后與西北、華中和華東電網之間的輸電新格局如圖1所示。異步運行的啟動,意味著西南電網與華中電網的頻率異步,依靠有功聯絡線輸送功率。頻率的變動規律與異步互聯前有所變化。

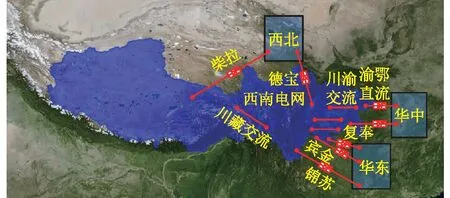
圖1 西南電網與各大電網間的輸電新格局Fig.1 New transmission pattern between Southwest Power Grid and other major power grids

西南電網異步運行前后相鄰兩周同一工作日的頻率見圖2。系統頻率由相量測量單元(pha-sor measurement unit,PMU)測得。

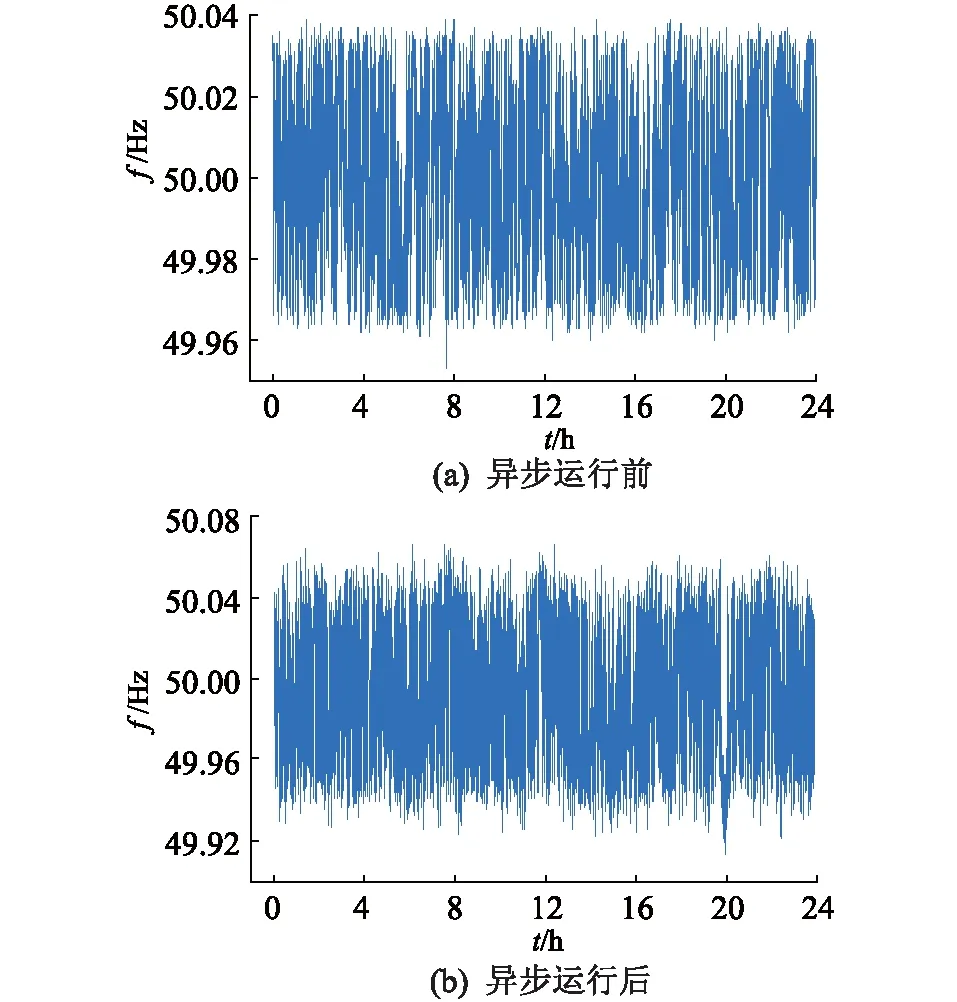
圖2 西南電網異步運行前后的系統量測頻率Fig.2 Measured system frequency of Southwest Power Grid before and after asynchronous operation

西南電網異步運行前后,t-1到t+12共14 d的頻率波動量超過±0.07 Hz,對期間直流FC動作次數進行統計,如表1所示。其中,t為異步運行啟動當日,t-1為異步運行前一日,t+1為異步運行后一日,以此類推。

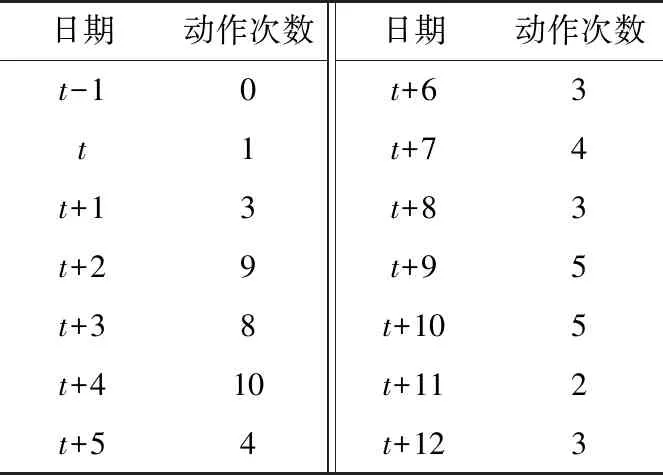
表1 直流FC動作次數Table 1 Action times of direct current FC

結合圖2與表1可知,西南電網異步運行后,系統頻率較異步運行前波動加劇,直流FC動作較為頻繁。

結合數據與轉子運動方程的理論分析可知,西南電網異步運行后系統的總慣量下降。當系統有功功率與負荷不匹配時,頻率波動幅度加劇。因此,負荷預測可以預先把控有功平衡、提前制定發電計劃、實施自動發電控制(automatic generation control,AGC)超前控制等,從負荷端抑制頻率波動。

西南電網異步運行前后共14 d的負荷曲線見圖3。圖中,14 d的最大、最小負荷分別為47 422 MW,27 840 MW。由圖3可知,西南電網的負荷呈周期性,負荷變化特征受異步互聯影響有限。異步互聯工程的啟用通常對負荷影響很小,電力負荷具有明顯的日周期特性。負荷存在極大值和極小值點,在極大值點,每日的負荷變化趨勢總體一致。但由于每日的負荷受生活習慣、氣象等因素影響,相同時間點的實時負荷存在一定差值。

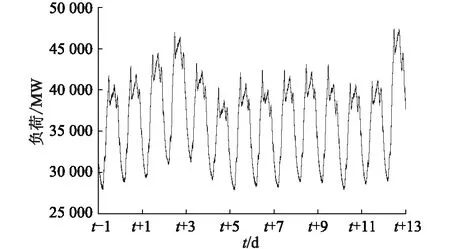
圖3 西南電網異步運行前后14 d的負荷曲線Fig.3 14-day load curve before and after asyn- chronous operation of Southwest Power Grid

西南地區分別以1 s,1 min為時間尺度的負荷波動幅值概率分布如圖4所示。可以看出,1 s時間尺度下,負荷波動范圍限制在100 MW以內,波動大于60 MW的概率不足1%,波動比較平緩。1 min時間尺度下,負荷波動主要集中在200 MW以內,波動變化在200 MW以上的概率不足1%。文中將秒級與分鐘級的負荷波動概率納入負荷預測過程,提高負荷預測精度。

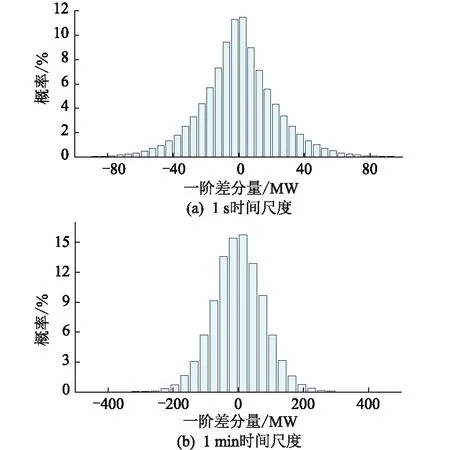
圖4 西南地區負荷波動幅值概率分布Fig.4 Probability distribution of load fluctuation amplitude in Southwest China

2 預測算法原理

根據西南電網負荷特點,文中提出一種新型混合算法對負荷進行預測。該算法在BP神經網絡預測日負荷水平的基礎上,使用SVR算法預測負荷曲線,并將待預測日已知的一段負荷數據與歷史相同時間節點的負荷數據進行比較,調整訓練集的權重。根據歷史數據的負荷波動幅值概率分布修正預測結果,提高模型預測精度及可靠性。

2.1 SVR原理

SVR算法分為ε-SVR模型和v-SVR模型[15]。ε-SVR模型的初始參數優化較為困難,v-SVR模型使用改進網格搜索算法可以得到較好的初始參數[16],文中所述SVR算法采用v-SVR模型。

對于訓練數據x=[x1,x2,…,xi,…,xn],對應的訓練目標為y,二者之間存在從特征集到目標集的映射關系f,即求解目標函數f(x) =wΦ(x) +b。其中Φ(x)為非線性函數；w,b為權值矩陣和對應偏置。SVR可訓練f(x)的風險函數最小化,即最大化分隔超平面。SVR訓練過程如圖5所示。

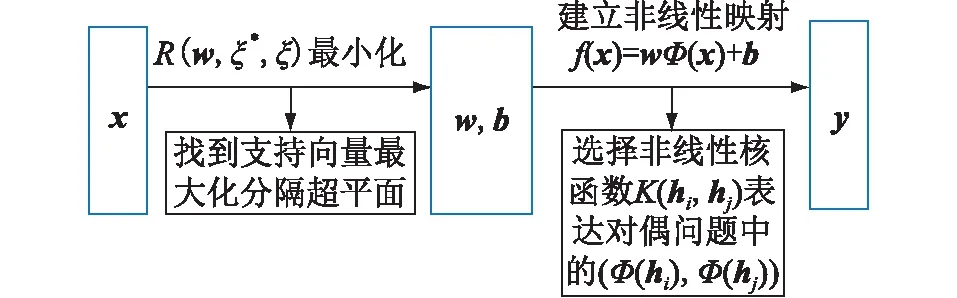
圖5 SVR模型訓練原理Fig.5 Training principle of SVR model

風險函數可表示為：

(1)

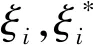
約束條件為：

(2)

式中：ε為線性不敏感損失函數。

構建拉格朗日函數為：

(3)

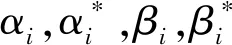
考慮Karush Kuhn Tucker(KKT)邊界條件和對偶問題,最優對偶變量和約束的乘積為0。

(4)

線性函數逼近式可表示為：

(5)

式中：K(x,xi)為SVR的核函數；b可由式(5)求得。

核函數通常分為4類。

(1) 線性核函數。

K(hi,hj)=〈hi·hj〉

(6)

式中：hi,hj為樣本集向量；〈hi·hj〉為hi和hj的內積。

(2) 多項式核函數。

K(hi,hj)=(〈hi·hj〉+1)d

(7)

式中：d為多項式的次數。

(3) 徑向基核函數。

K(hi,hj)=e-‖hi-hj‖2/(2σ2)

(8)

式中：σ為徑向基核函數的帶寬。

(4) Sigmoid核函數。

K(hi,hj)=tanh(a〈hi,hj〉+c)

(9)

式中：tanh(·)為雙曲正切函數；a,c為相關參數。

2.2 基于相關影響因素的最大負荷值預測

文獻[17—20]指出,電力系統的負荷與負荷日的類型相關。考慮天氣及是否工作日等因素,針對每日預測的最大負荷值,選取相關特征如表2所示。

表2 影響負荷的相關特征Table 2 Related features affecting load

上述每個相關特征都對應BP神經網絡的特征,將每個參數歸一化處理后,輸入BP神經網絡進行訓練。對于西南地區,每個小地區同一日的氣候數據通常不同。收集到的氣象數據僅代表局部區域特點,不能很好地反映整個區域的氣象水平。針對西南大區域的負荷預測,采集到每個小區域的氣象數據后,大區域的總體氣象特征可以表示為：

(10)

式中：xij為小區域j中特征量i的氣象特征；Sj為小區域j的面積；N為區域數量。

針對該類型問題,通常使用神經網絡方法進行預測。神經網絡具有反饋調節網絡權值的能力,對于非線性回歸問題有較好的預測效果。基于表2中的特征,以每日最大負荷為目標訓練BP神經網絡,然后對目標進行預測。BP神經網絡訓練結構示意如圖6所示。

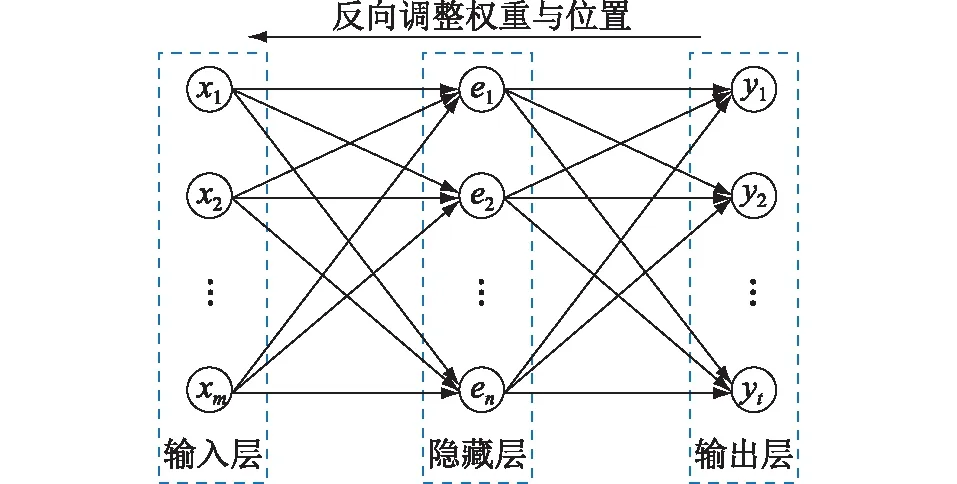
圖6 BP神經網絡訓練結構Fig.6 Training structure of BP neural network

訓練神經網絡可使特征量以各自的權重表達當日最大負荷值,使預測值與實際值的誤差在訓練集基礎上達到總體最小。模型訓練完成后可以根據待預測日的天氣預測最大負荷值,為后續模型的準確預測提供基礎。

2.3 新型混合算法

負荷量通常會根據工作日、休息日、節假日等特殊日期發生相應變化。目前已有研究將該類特殊日期作為特征值對模型進行訓練[3,21]。同類型日期的負荷數據通常具有較高的重復度,不同類型日期的負荷數據通常差異較大。

實際電網運行中,特征值的選擇不限于表2,還可能存在國民經濟提升、產業結構改變、自然天氣突變等不可預知因素。這些因素特征不穩定且提取困難。文中提出一種新型混合算法,將SVR算法和BP神經網絡算法相結合。基于氣象數據采用BP神經網絡預測負荷水平,利用所得負荷水平作為SVR算法訓練集的選取依據。從歷史數據中選取接近該日預測負荷最大值的數據作為SVR的訓練集。模型訓練過程中使用搜索網格算法優化SVR的參數與核函數。獲得混合算法模型的預測結果后,通過西南地區歷史負荷波動幅值概率分布修正SVR結果并滾動更新負荷預測結果,使預測結果能更適應西南地區的負荷特點。具體模型訓練流程如圖7所示。

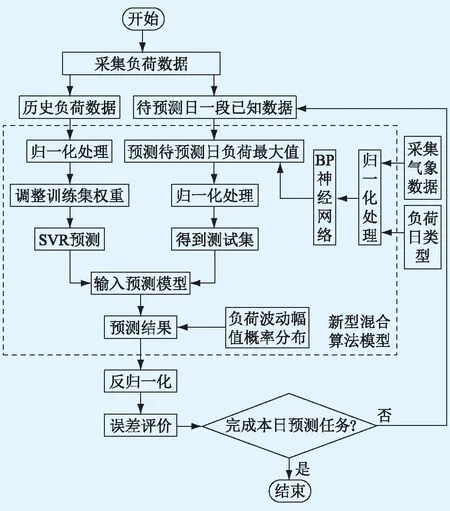
圖7 新型混合算法模型訓練流程Fig.7 Training process of novel hybrid algorithm model

SVR模型的訓練從訓練集選取待預測日已知的一段時間負荷數據作為測試樣本的特征集,用于輸入模型預測整日的負荷曲線。訓練集的選取通過歷史日負荷峰值與當日預測峰值的差異調整訓練集的權重,差異較小的權重大,差異較大的權重小。目標集選取剩下時間段待預測的負荷。將當日已知一段時間的負荷測試樣本輸入模型,預測當日剩余時間的負荷。并隨著時間推移,對當日負荷進行滾動預測。訓練SVR的數據劃分方式見圖8。

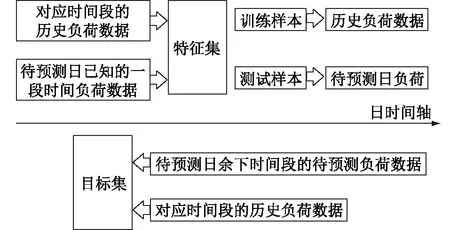
圖8 訓練SVR的數據具體劃分方式Fig.8 The specific division of data for training SVR

2.4 誤差評價標準

誤差評價標準是用于比較預測值與實際值之間誤差的指標。用平均絕對百分比誤差(mean absolute percentage error,MAPE)和均方根誤差(root mean square error,RMSE)表示短期負荷Pl的預測誤差。MAPE用來衡量預測值與實際值之間的相對誤差大小,RMSE用來衡量預測值與實際值之間誤差的離散程度。

(11)

(12)

式中：M為誤差評價的樣本數；Pl,pre,Pl,real分別為負荷預測值和實際值。

3 負荷預測算例

算例選取西南區域電網異步運行后一個月的歷史負荷作為新型混合算法模型的訓練集數據庫,同時采集對應時間段的相關氣象數據作為特征預測當日最大負荷值。

3.1 工作日負荷預測結果分析

此次預測選擇周一至周五任意工作日作為測試樣本。將已知待預測日負荷的前30 min數據作為測試樣本的特征集,后23.5 h的數據作為測試樣本的目標集。采用圖7的訓練流程,模型訓練完成后,使用測試集進行檢驗。使用新型混合算法所得的第1次負荷預測結果及絕對誤差(預測值與實際值之差的絕對值)如圖9所示。

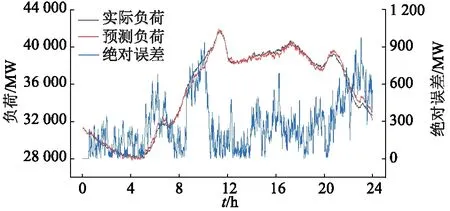
圖9 工作日第1次預測結果及絕對誤差Fig.9 The first forecasting result and absolute error on weekdays

第1次負荷預測的eMAPE為0.940 9%,eRMSE為348.46 MW。預測間隔選取30 min,該日一共進行47次滾動預測,從當日00:30開始,每次時間步進30 min,將實時獲得的每30 min負荷數據作為SVR的特征集,進而預測后續負荷,每次預測誤差如圖10所示。

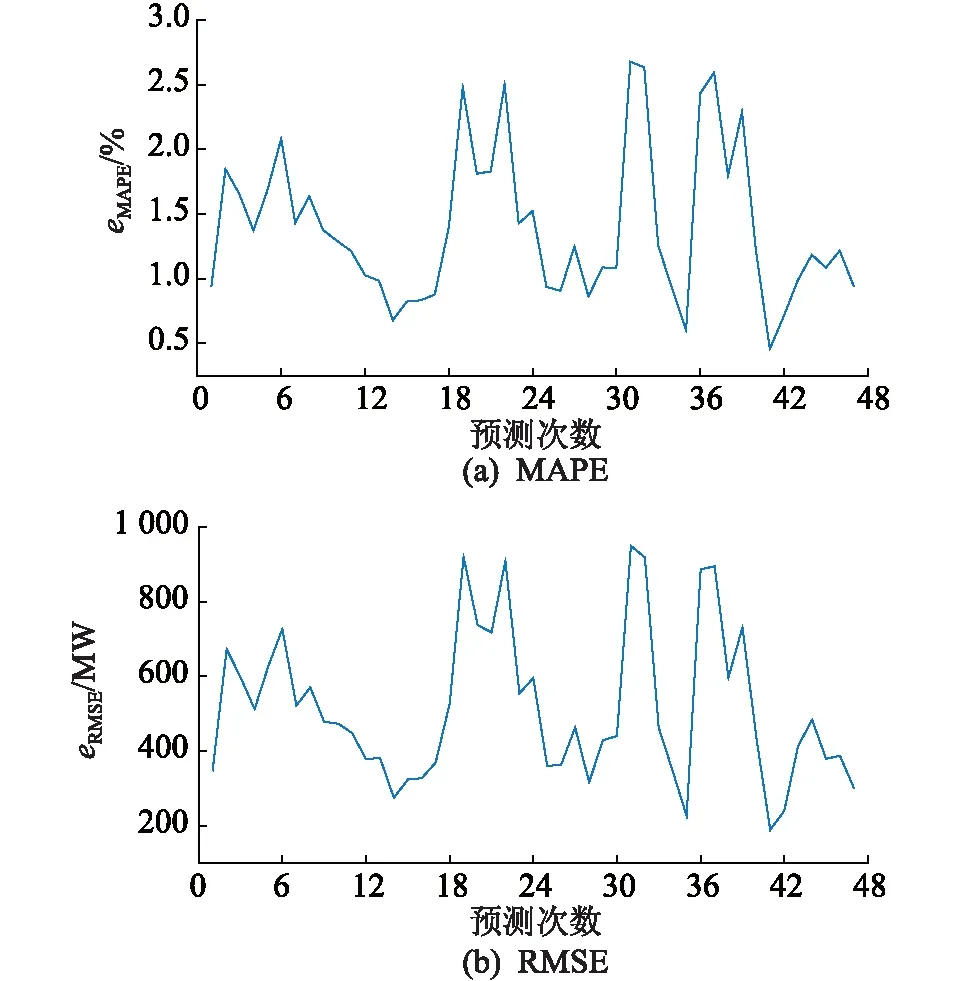
圖10 工作日負荷預測誤差Fig.10 Load forecasting error on weekdays

由圖10可知,工作日負荷預測eMAPE均處于2.7%以下,eMAPE的平均值為1.401 2%,eRMSE均處于950 MW以下。

3.2 休息日負荷預測結果分析

與工作日預測方法相似,休息日同樣選取30 min作為模型更新步長,第1次預測將前30 min作為測試樣本特征集,后23.5 h為目標集。第1次預測結果如圖11所示。

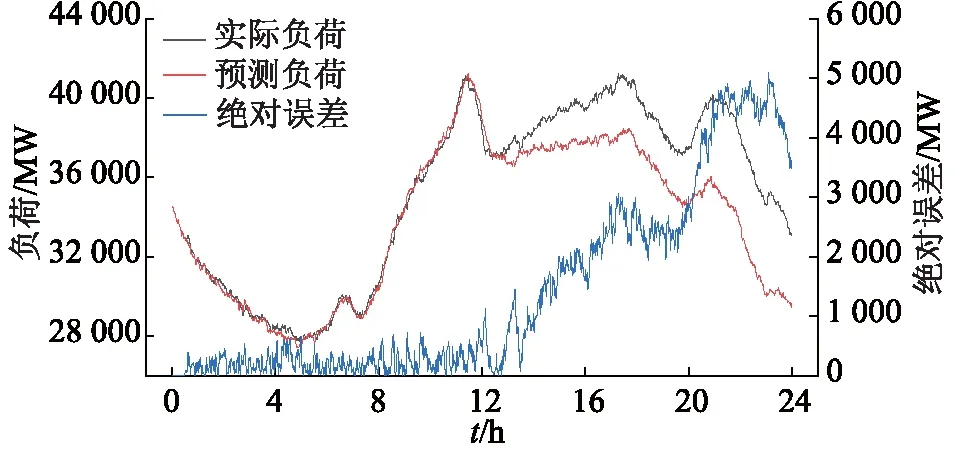
圖11 休息日第1次預測結果及絕對誤差Fig.11 The first forecasting result and absolute error on weekends

由圖11可知,當對休息日進行預測時,混合模型對前半日的預測較為準確,后半日預測誤差較大。隨著待預測日時間的推移,模型將進行多次預測,每次步長30 min,當進行第27次預測時,模型受實時負荷影響,不斷修正預測結果,如圖12所示。

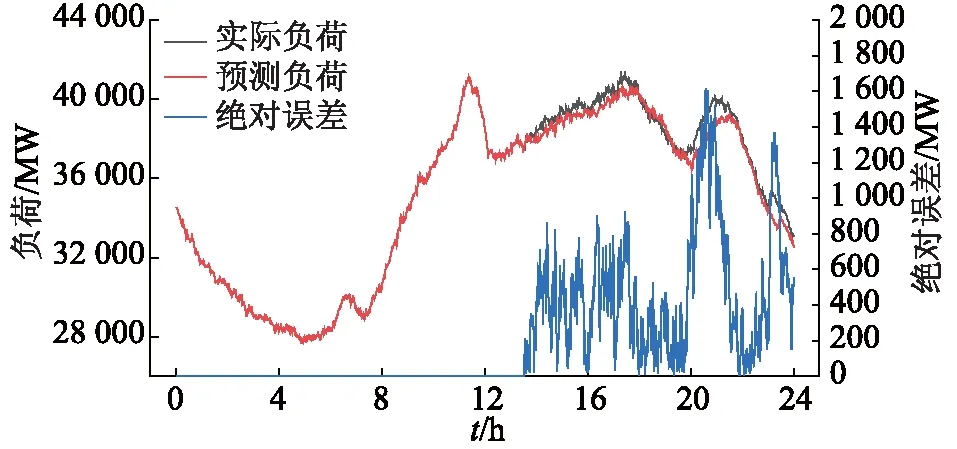
圖12 休息日第27次預測結果及絕對誤差Fig.12 The 27th forecasting result and absolute error on weekends

隨著預測日當天時間的推移,不斷會有當天的實際負荷數據生成,這些數據比歷史數據更有意義。每隔30 min,模型將最近30 min的實時負荷數據作為模型的輸入,預測當日的后續負荷。當突發事件發生時,模型會根據實時數據滾動更新后續預測結果。該新型混合預測算法選定的時間步長為30 min,每經過30 min,訓練模型會拋棄預測當天相對久遠的數據,使用新數據作為SVR測試集特征,回歸預測當日剩余時間的負荷,每日一共滾動預測47次。使用此方法可以一定程度減小隨機事件造成的誤差。預測日共47次預測誤差如圖13所示。

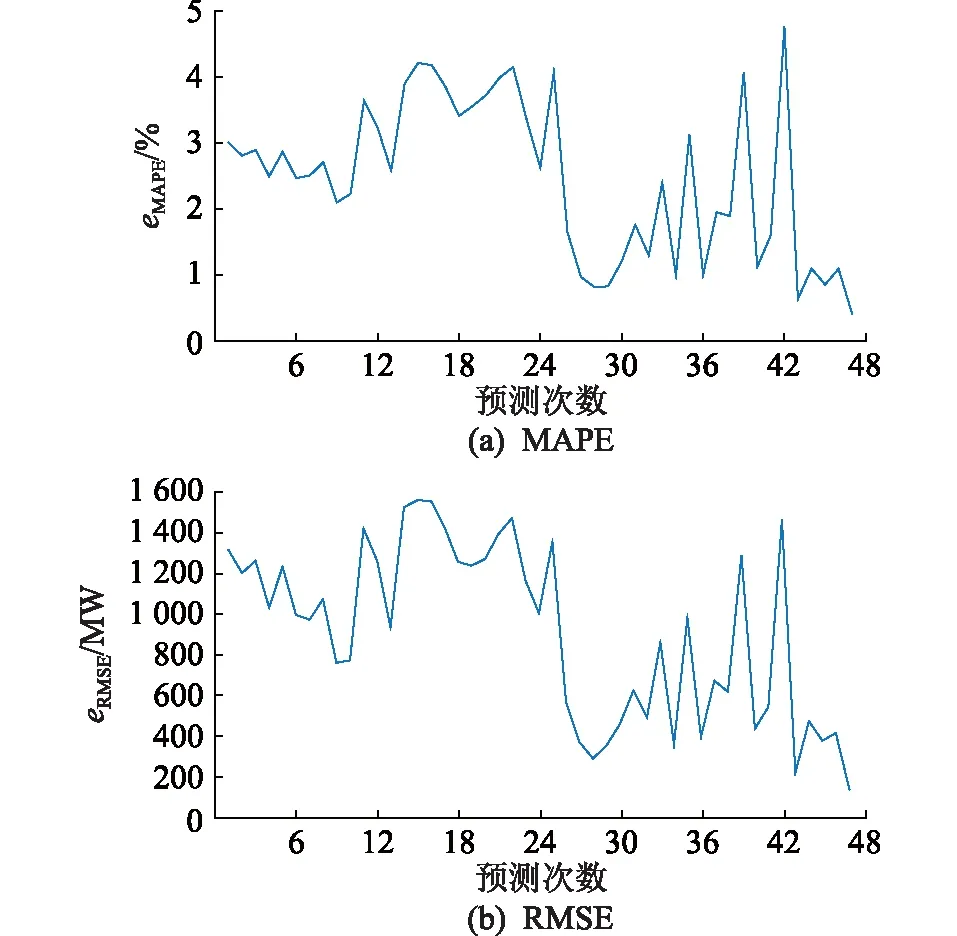
圖13 休息日負荷預測誤差Fig.13 Load forecasting error on weekends

由圖13可知,當待預測日為休息日時,使用模型進行第1次預測,結果顯示該日后半段負荷預測誤差較大。經過27次預測后,實際負荷參與混合模型訓練,可對預測結果進行調整。待預測日的后半段預測結果與實際負荷誤差減小,預測精度提升。從第27次預測開始,eMAPE和eRMSE減小,可見實時負荷數據的更新可對模型進行修正。

3.3 負荷預測誤差比較

為體現BP神經網絡對負荷預測結果的影響,基于預測和實際負荷分別對模型進行訓練,14 d的eMAPE平均值分別為1.67%,1.55%。可見,BP神經網絡的預測精度與實際情況的誤差較小,即精度較高。

使用文中所提新型混合算法與文獻[10—11]所述的LSTM、文獻[22]所述的雙層隨機森林算法進行比較,eMAPE結果如表3所示。

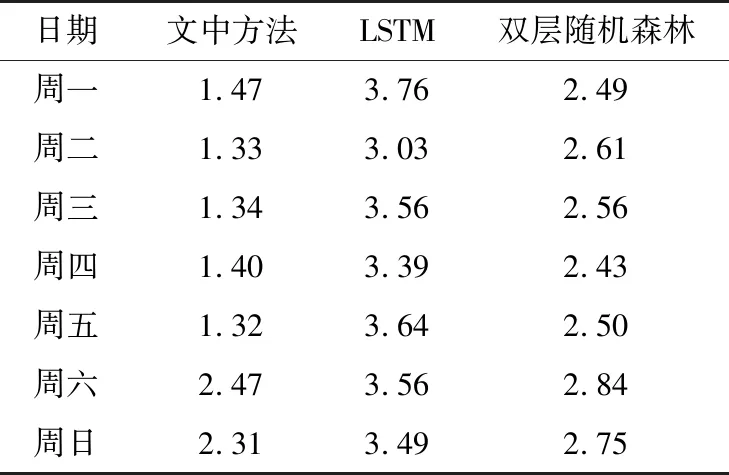
表3 3種機器學習方法的eMAPE比較Table 3 eMAPE comparison of three machine learning methods %

4 基于負荷預測結果的頻率仿真

為驗證負荷預測結果對西南電網的頻率控制效果,基于幾種機器學習方法的負荷預測結果,利用BPA仿真軟件對負荷波動下的西南電網頻率響應進行仿真。仿真模型基于西南異步后的系統,選取真實系統平衡運行時某一時刻的潮流作為潮流仿真數據,選取該時間節點后15 min的負荷數據進行頻率響應仿真。實際及預測負荷如圖14所示,圖中選取與文中預測精度更接近的雙層隨機森林算法進行比較。

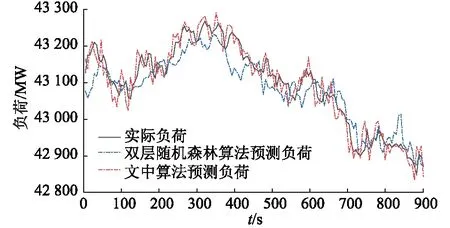
圖14 實際負荷及兩種算法的負荷預測結果Fig.14 Actual load and load forecasting results of two algorithms

仿真過程中,設置負荷波動為：

ΔPL(i)=PL(i+1)-PL(i)

(13)

式中：PL(i)為當前時刻的實際負荷；PL(i+1)為下一仿真時刻的實際負荷；ΔPL(i)為仿真設置的負荷變化量。

根據算法預測結果,可提前安排有功功率。設置系統有功增量為：

ΔPG(i)=PG(i+1)-PG(i)

(14)

式中：PG(i)為當前時刻的系統有功發出值；PG(i+1)為下一仿真時刻的負荷預測值；ΔPG(i)為仿真設置的有功變化量。

仿真基于實際西南電網簡化后的模型,包括282臺發電機,1 825條母線。模型考慮了發電機的勵磁系統、系統穩定器、調速器等數學模型。設置仿真步長為0.01 s,總時長為900 s,負荷類型為40%恒功率負荷及60%恒阻抗負荷。負荷每隔6 s產生一次擾動,負荷擾動曲線如圖15所示。

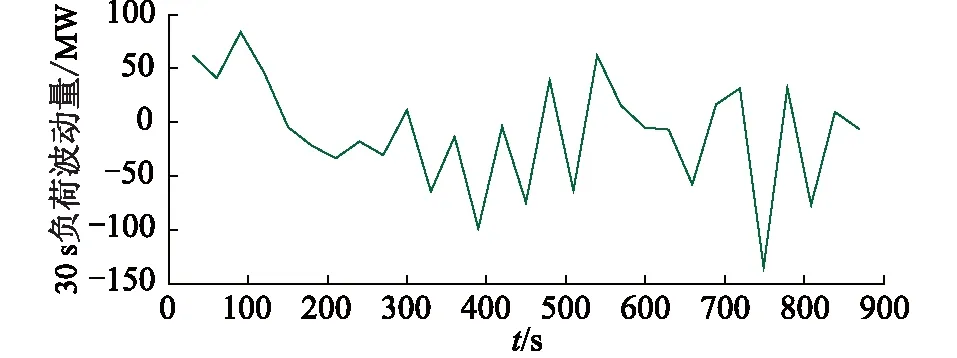
圖15 負荷擾動曲線Fig.15 Load disturbance curve

作為典型含高比例水電的電網,西南電網水電裝機總容量突破8 000萬kW,水電容量占比70%以上,頻率穩定需要網內機組一次調頻與AGC相互配合動作。調頻主要依靠水電機組完成,由于水電機組水錘效應,初始功率變化與導葉開度變化相反,造成水輪機環節相位滯后,高比例水電系統調頻過程中小干擾穩定問題突出。大型水電機組的AGC信號傳輸延遲大約20 s,AGC控制調節到位的時間則需按照爬坡速率折算(1 min可調整裝機容量的15%～20%,即8 000 MW/min)。由圖15可知,15 min內的負荷波動在200 MW以內,故AGC控制在2 s內自動調用發電機旋轉備用容量。算例負荷數據選取該時間節點后15 min的負荷進行仿真,西南電網各電站可根據30 s時段負荷預測結果調整發電出力。故在15 min內,AGC控制可根據負荷預測結果實時調整發電計劃約30次。對西南電網一次調頻下該段負荷的頻率響應進行仿真,不同負荷預測算法的頻率響應結果如圖16所示。

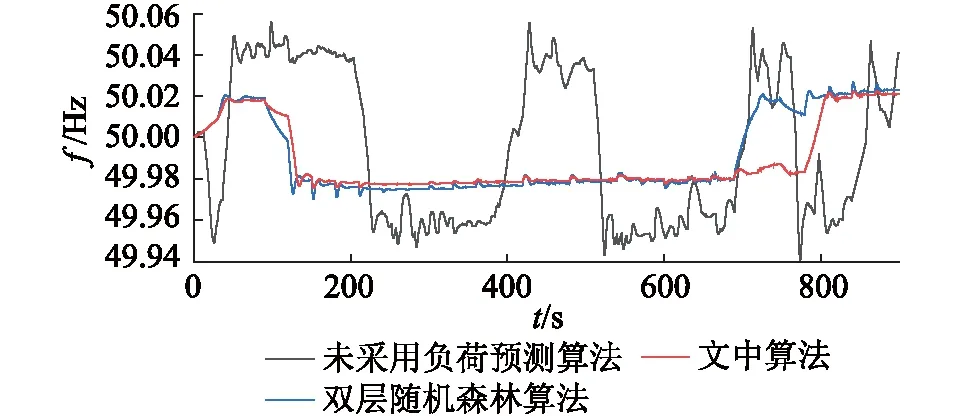
圖16 不同算法預測的西南電網一次調頻頻率波動Fig.16 Frequency fluctuation of primary frequency modulation in Southwest Power Grid predicted by different algorithms

由圖16可知,在一次調頻作用下,相對未采用負荷預測算法(實際的頻率波動)而言,根據負荷預測結果制定的發電計劃可極大抑制頻率波動最大值,且在電網一次調頻作用下,系統頻率波動有所減緩。采用文中新型混合算法、雙層隨機森林算法、未采用負荷預測算法的頻率響應eRMSE分別為0.022 7 Hz,0.026 0 Hz,0.037 1 Hz。相較雙層隨機森林算法的預測結果,使用文中提出的新型混合算法的預測結果對系統進行一次調頻,頻率波動更小。

5 結語

西南電網異步運行后,有功不平衡導致頻率問題突出、直流FC裝置動作頻繁。為解決有功不平衡導致的頻率問題,文中提出了采用組合BP神經網絡和SVR算法的新型混合算法用于電力系統負荷預測。基于氣象數據、電力系統歷史數據以及預測日當天已有數據,采用BP神經網絡對當日最大負荷進行預測,從歷史數據選擇與最大負荷最相近的訓練樣本建立模型。采用當日一段已知數據作為SVR模型的輸入,結合BP神經網絡劃分的訓練集訓練模型,預測當日剩余時間的負荷。誤差分析結果表明,新型混合算法所得結果滿足負荷預測需求。同時,基于新型混合算法所得負荷預測結果制定的發電計劃對頻率控制有著積極作用,可極大改善系統頻率偏移與波動程度。

下一步可從如下方面開展研究：基于豐富的歷史數據庫建立考慮多特征的預測模型；優化預測模型結構、核心算法等,如選擇預測精度更高的人工智能網絡。旨在進一步提高電力系統負荷預測精度,有效制定發電計劃,抑制電網頻率波動。