基于峰值補償的連續變量量子密鑰分發方案*

毛宜鈺 王一軍 郭迎 毛堉昊 黃文體

1) (中南大學自動化學院， 長沙 410083)

2) (中南大學商學院， 長沙 410083)

3) (湖南航天建筑工程有限公司， 長沙 410205)

4) (中南大學計算機學院， 長沙 410083)

在實際的連續變量量子密鑰分發系統中， 接收端模數轉換器的有限采樣帶寬會導致脈沖峰值采樣結果不準確， 從而使參數估計過程產生誤差， 給竊聽者留下了安全性漏洞.針對這個問題， 本文提出一種基于峰值補償的連續變量量子密鑰分發方案， 利用高斯脈沖的基本特性來估計每個脈沖的最大采樣值與脈沖峰值之間的偏差， 從而對該采樣值進行峰值補償， 使系統得到正確的采樣結果.本文詳細分析了有限采樣帶寬對系統安全性的影響， 闡述了峰值補償的具體步驟， 并討論了峰值補償前后系統估計的過噪聲差別， 及其在高斯集體攻擊下的安全性.仿真實驗結果表明， 該方案能準確找到每個脈沖的峰值， 糾正系統的參數估計誤差.與不采用峰值補償的方案相比， 本方案消除了系統重復頻率對密鑰比特率的限制， 具有更長的安全傳輸距離和更高的密鑰比特率.

1 引 言

量子密鑰分發是量子技術的一項重要應用， 它能使遠距離的通信雙方在不安全的環境中建立一串無條件安全的密鑰， 且這種無條件安全性是由量子力學的基本定律保證的.近年來， 量子密鑰分發技術取得了很大的進展， 主要可以分為離散變量量子 密 鑰 分 發[1-3](discrete-variable quantum key distribution， DVQKD)和連續變量量子密鑰分發(continuous-variable quantum key distribution，CVQKD)兩大類[4，5].相比于DVQKD， CVQKD將密鑰編碼在光場的連續正則分量上， 一般以相干激光作為光源， 并采用平衡零差探測器進行探測，具有更高的密鑰率， 且能更好地與現有的光通信系統相結合[6，7].利用連續變量進行密鑰分發的概念在1999年由澳大利亞學者Ralph[8]首次提出， 受到了量子保密通信研究者們的廣泛關注.2002年，Grosshans和Grangier[9]創造性地提出了一種基于弱相干態高斯調制和零差檢測的CVQKD協議，即著名的GG02協議.該協議充分體現了CVQKD的優勢， 具有重大的實際意義， 但它使用的正向協商方法使協議受到3 dB傳輸損耗的限制.為了解決這個問題， Grosshans等[10]在2003年又提出了反向協商方案， 該方案可以突破3 dB損耗限制，并且具有更高的密鑰率.此后， 在GG02的基礎上，研究者們提出了大量改進方案， 推動了CVQKD的迅速發展.例如， Weedbrook等[11]在2004年提出一種基于外差檢測的no-switching協議， 使接收方能同時測量相干態的兩個正則分量來提取密鑰.2008年， Pirandola等[12]提出一種雙路方案來提升協議的性能.2009年， Leverrier和Grangier[13]提出了具有更遠安全距離的離散調制方案， 并證明了其在線性量子信道條件下的安全性.2012年，Weedbrook等[14]提出以熱態或加噪相干態為光源的 CVQKD 方案， 并分析了其在微波頻段的可行性.2015年， Vladyslav等[15]提出了一維調制CVQKD方案， 通過只調制一個正則分量來簡化系統的實現過程.隨著協議的不斷改進和發展， 其相應的安全性證明也在持續跟進.2004年， Grosshans和Cerf[16]證明了CVQKD在單體攻擊下的安全性.兩年后，Navascués等[17]又發現了高斯攻擊是針對高斯調制相干態CVQKD協議的最優攻擊， 同年， García-Patrón等[18]也用另一種方法進一步證明了高斯攻擊的最優性.2009年， Renner等[19]利用de Finetti定理證明了相干攻擊和集體攻擊對DVQKD和CVQKD而言都是等價的， 使得大部分CVQKD協議都可以基于簡單的高斯集體攻擊來進行安全性分析.2010年， Leverrier等[20]在CVQKD協議的理論安全性分析中考慮了有限長效應的影響， 并且在2015年完成了高斯調制相干態CVQKD協議的組合安全性證明[21].

盡管高斯調制相干態CVQKD協議可以保證理論上的無條件安全， 但在實際實現的過程中， 器件的不完美或噪聲等因素都可能會被竊聽者Eve利用來獲取信息， 使系統的無條件安全性受到影響.目前已經提出的幾種針對實際CVQKD系統的攻擊方案有: 特洛伊木馬攻擊[22]、校準攻擊[23]、本振光抖動攻擊[24]、波長攻擊[25-27]、飽和攻擊[28]、零差探測器致盲攻擊[29]、種子光注入攻擊[30]、不完美的態制備問題[31]及有限采樣帶寬影響[32]等.其中， 有限采樣帶寬影響是指接收端的模數轉換器(analog-to-digital converter， ADC)的有限采樣帶寬會降低密鑰率的下界并限制密鑰率和系統重復頻率之間的關系， 從而被竊聽者利用來隱藏其攻擊.為了解決有限采樣帶寬的影響， 研究者們也提出了相應的應對措施.例如， Wang等[32]提出了一種雙采樣檢測方案， 用兩個由同一電路觸發的ADC同時對零差探測器的輸出和本振光進行采樣， 來使散粒噪聲方差的測量值與量子態正則分量的測量值相對應， 從而保證接收方Bob能估計到正確的信道參數.但由于光電二極管(positive intrinsicnegative， PIN)和其他的光電因素之間存在差異，可能會使一個ADC的峰值與非峰值之比與另一個之間存在非線性， 從而對參數估計結果造成影響.Li等[33]利用一個動態時延調節模塊和統計功率反饋控制算法來消除有限采樣帶寬的影響， 使Bob總是能采到脈沖的峰值.但這種方法需要進行多步時延調節才能取得較好的效果， 可能會導致大量密鑰的浪費， 也增加了系統運行的時間成本.

針對實際CVQKD系統的有限采樣帶寬問題，本文提出了一種峰值補償方案， 通過對接收端的采樣結果的分析來判斷采樣值是否為峰值， 并在未采到峰值時對采樣結果進行補償， 使通信雙方在后處理過程中能夠正確估計信道參數， 消除由有限采樣帶寬影響導致的安全性漏洞.這種方法可以直接在采樣后的數據處理階段完成， 不需要增加任何額外的設備， 相比之前提出的雙采樣方案和動態時延調節方案， 具有更高的準確性.本文第2節簡要介紹ADC的有限采樣帶寬對高斯調制相干態CVQKD系統的影響和峰值補償的主要步驟; 第3節詳細地討論峰值補償后的參數估計過程及系統在集體攻擊下的安全性; 第4節對全文進行總結.

2 實際CVQKD系統的峰值補償方案

2.1 有限采樣帶寬影響

在高斯調制相干態CVQKD協議中， 發送方Alice選擇兩組均值為0， 方差為VX=VAN0的服從高斯分布的隨機數， 用振幅調制器和相位調制器將這兩組數據分別編碼在信號光脈沖的正則分量XA和PA上， 得到相干態|XA+iPA〉， 并將它們同本振光一起通過偏振復用和時分復用發送給接收方Bob.Bob使用的接收裝置如圖1所示， 偏振分束器將接收到的信號光和本振光分離出來， 本振光接著被一個10∶90的分束器分離成兩部分， 一部分連接光電二極管用于監測本振光強度， 另一部分與信號光干涉進行零差探測.本振光路上的相位調制器隨機將相位調整為0或 π /2 來選擇測量基.最后，ADC以頻率fsamp對零差探測器的輸出結果采樣，采樣后的數據保存到Bob的電腦中進行后處理.在這個過程中， Bob測量到的相干態的正則分量值由零差探測器輸出電脈沖的峰值決定[33].當ADC的采樣頻率無限大時， Bob總是能準確采到脈沖的峰值得到信號光的正則分量， 從而估計到正確的信道參數.但在實際系統中， ADC的采樣帶寬是有限的， 這使得采樣值可能與脈沖的峰值之間存在偏差， 如圖2所示.

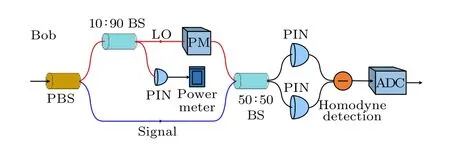
圖1 CVQKD系統的接收端設備結構圖.PBS為偏振分束器， BS為光分束器， PM為相位調制器， PIN為光電二極管， ADC為模數轉換器Fig.1.Structure of receiver’s apparatus of a CVQKD system.PBS， polarization beam splitter; BS， beam splitter;PM， phase modulator; PIN， positive intrinsic-negative;ADC， analog-to-digital converter.

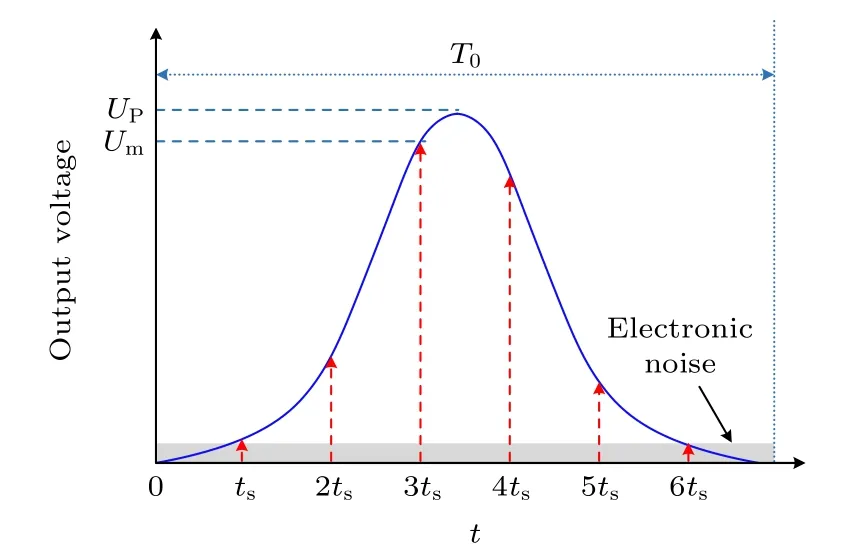
圖2 零差探測器輸出脈沖的時域波形， 箭頭表示采樣位置.ts 為 采 樣 間 隔， U p 為 脈 沖 的 峰 值， U m 為 最 大 測 量 值，T0為脈沖持續時間Fig.2.Time-domain shape of an output pulse from the balanced homodyne detector.ts ， sampling interval; U p ， peak value of the pulse; U m ， maximal measurement value; T 0 ，duration of each pulse.

通常， 對于一個高斯調制相干態CVQKD系統，零差探測器的帶寬遠遠大于系統重復頻率frep[34，35]，因此能保證零差探測器工作在其線性區域， 且探測器的響應相對于輸入光場的正則分量是線性的.在這種情況下， 探測前后的脈沖信號一般為高斯分布， 波形函數為[32，33，36]

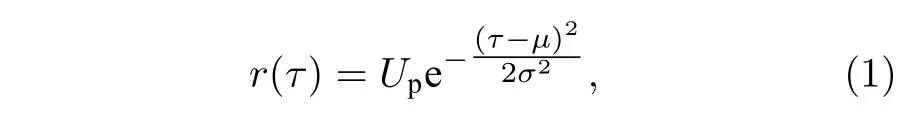
其中，Up為高斯脈沖的峰值，μ和σ2分別代表均值和方差.為了簡單起見， 我們選擇μ=T0/2 ，σ2=T0/8 ，T0=1/frep為脈沖持續時間.如圖2所示， 在一個脈沖時間T0內， ADC進行了多次采樣， 采樣間隔為ts=1/fsamp， 由于受到有限采樣帶寬的影響， 最大采樣值Um和Up之間存在偏差， 定義為

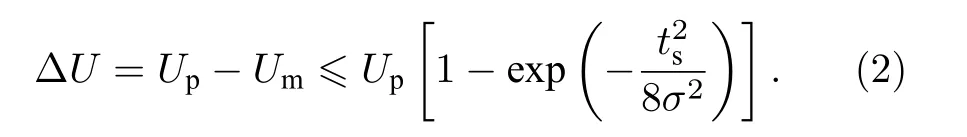
因此， 我們可以得到Um和Up之比為

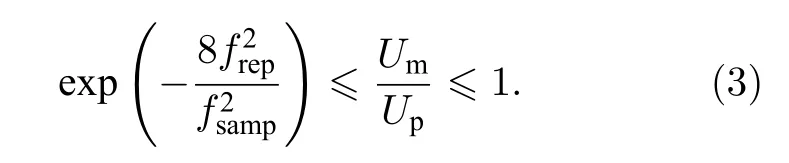
在這種情況下， Alice和Bob會錯誤地估計信道參數t和ε， 得到[32]

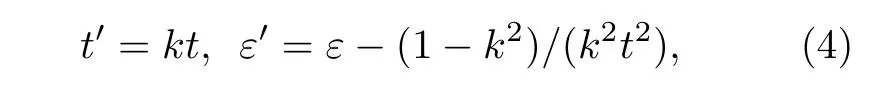
其中:k=Um/Up;t=ηT，η為零差探測器的探測效率，T為信道透射比;ε為系統的過噪聲;t′和ε′分別表示t和ε的估計值.因此， 在沒有采到脈沖的峰值時， Alice和Bob會錯誤地估計系統的過噪聲， 給竊聽者留下安全漏洞.

2.2 峰值補償

為了消除由ADC的有限采樣帶寬引入的安全性漏洞， 我們在圖1的ADC后引入一個峰值補償模塊， 以實現峰值監測與補償.以圖2為例， 我們的峰值補償方案包括以下幾個步驟.1)對于一個脈沖時間T0內的所有采樣值{U1，U2，U3，U4，U5，U6}，找出其最大值點Um=U3以及與Um相鄰的兩個采樣值U2和U4.2)當U2=U4時， 可以判斷Um為峰值點; 當U24時， 可以判斷Um＜Up， 且根據高斯脈沖的性質， ΔU可由(5)式得到:

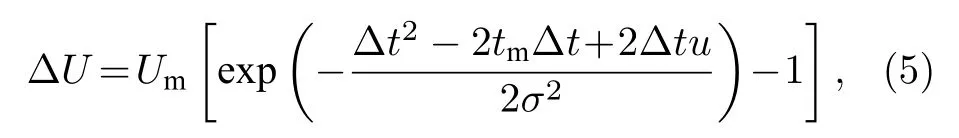
其中，tm=3ts為最大采樣值對應的采樣時間;Δt=tm-tp，tp為脈沖峰值對應的采樣時間.在已知U2和U4的前提下， 可得

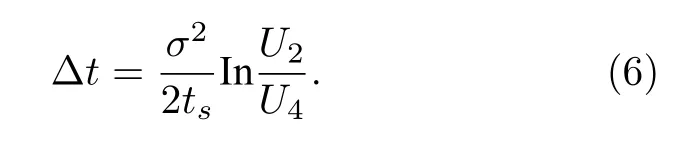
3)用得到的ΔU補償Um， 可得正確的脈沖峰值Up.

圖3(a)是在系統重復率為120 MHz、采樣頻率為1 GHz時一串高斯脈沖的被采樣情況， 在這種情況下每個脈沖的最大采樣值都不是脈沖的峰值點.圖3(b)是對最大采樣值進行峰值補償之后的采樣情況， 我們發現補償后的值剛好是每個脈沖的峰值點， 證明了提出的峰值補償方案的有效性.

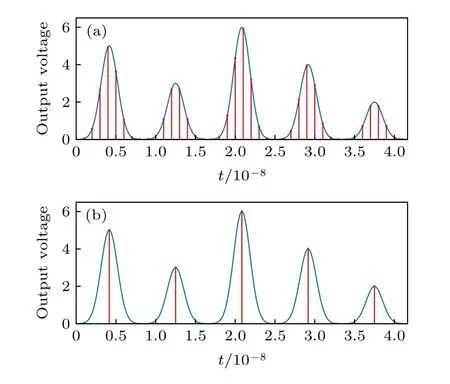
圖3 (a)有限采樣帶寬影響下的高斯脈沖時域采樣情況;(b)峰值補償后的采樣值.其中藍色線表示脈沖時域波形，紅色圓點代表采樣值Fig.3.(a) Sampling positions of Gaussian pulses effected by finite-sampling bandwidth; (b) sampling values after peak compensation.The blue line represents the time-domain shape of the pulses， and the red dots represent the sampled values.

3 基于峰值補償的CVQKD系統的安全性分析

3.1 參數估計

2.1 節分析了在有限采樣帶寬影響下， Alice和Bob估計的信道過噪聲ε會小于其真實值， 從而高估系統的密鑰率.本節分析峰值補償后系統對信道參數的估計.

在量子傳輸過程結束后， Alice和Bob共享兩個相關向量x=(x1，x2，···，xN) 和y=(y1，y2，···，yN)， 其中N表示傳輸的脈沖數目.它們之間的關系可以表示為[37]

其中，z表示系統的總噪聲， 服從均值為0， 方差為的高斯分布.N0表示系統的散粒噪聲，Vel=velN0表示零差探測器的電噪聲，ξ=εN0表示信道過噪聲， 這些參數都以它們各自的單位表示.在不采取峰值補償時，x，y與系統參數之間的關系可以表示為

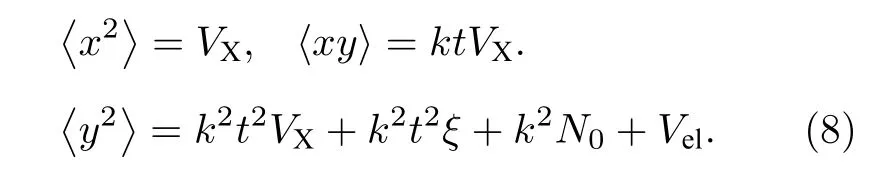
從而估計的信道參數如(4)式所示.在采取峰值補償時， 由于補償后的， 使得k=1 ， 因此估計的信道參數

圖4給出了在不同信道過噪聲下的估計過噪聲隨系統重復率的變化情況.從上到下的曲線分別代表ε=0.04，ε=0.02，ε=0.01 時的結果.顯然， 在不進行峰值補償時， 估計的過噪聲會隨系統重復率的增加而減小， 這意味著系統重復率越高， Eve越容易隱藏自己; 而在進行峰值補償后， 估計的過噪聲在不同系統重復率下都保持恒定.

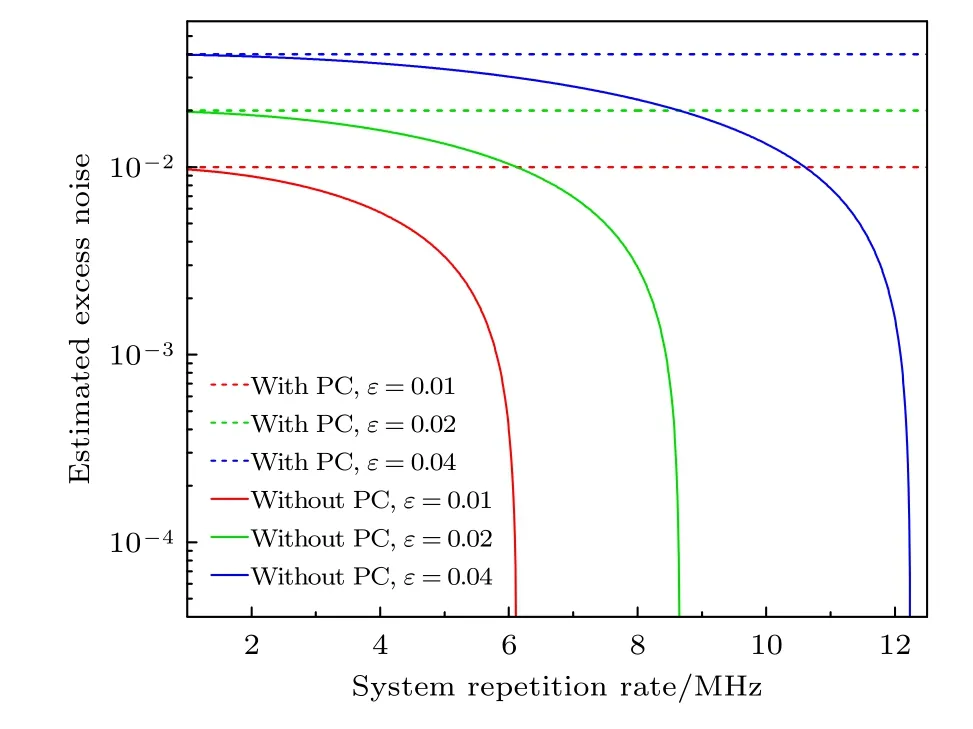
圖4 不同信道過噪聲情況下的估計過噪聲隨系統重復率的變化.圖中PC表示峰值補償(peak-compensation， PC)Fig.4.The estimated excess noise as a function of the system repetition rate under different channel excess noise.PC in the figure represents peak-compensation.

3.2 集體攻擊下的密鑰率

對于一個CVQKD系統， 給定參數VA，T，ε，η和vel， Alice和Bob可以計算出他們共享的信息量IAB和Eve可獲得的最大信息量χBE.因此， 在集體攻擊下， Alice和Bob可獲得的安全密鑰率為

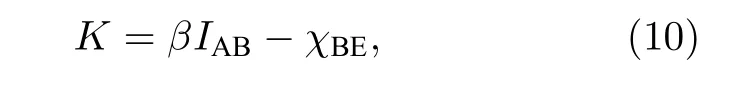
其中，β表示反向協商效率.且

其 中:V=VA+1 ;χtot=χline+χhom/T表 示 系 統的總噪聲，χline=T-1+ε-1 是信道輸入過噪聲，χhom=[(1-η)+vel]/η是零差探測器的等效輸入過 噪 聲;G(x)=(x+1)ln(x+1)-xlnx;λi是 表示量子系統的協方差矩陣的辛本征值， 其中λ1，2為λ3，4為

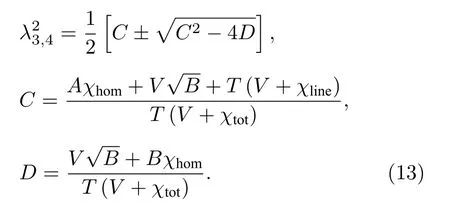
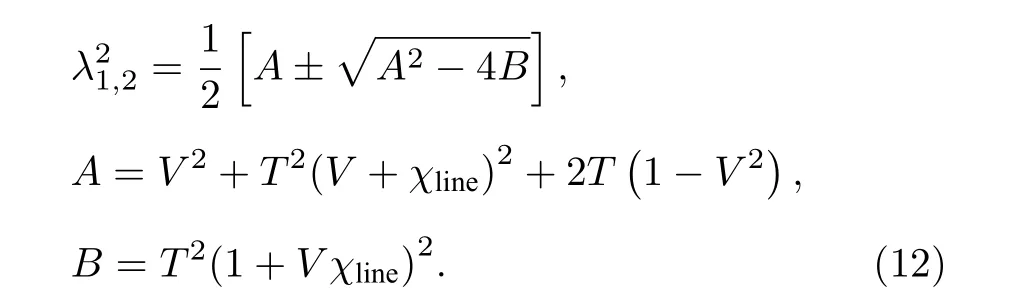
λ5=1.根據得到的安全密鑰率， 可求出系統的密鑰比特率為

在不進行峰值補償的情況下， 當系統估計的過噪聲為ε′時， 實際的過噪聲為

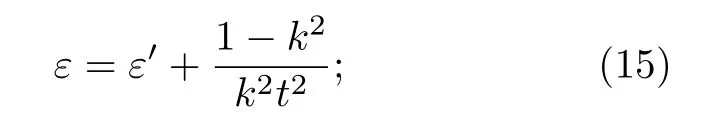
在進行峰值補償的情況下， 實際的過噪聲等于估計的過噪聲.圖5(a)給出了不同系統重復率frep=2，5，8MHz 的安全密鑰率隨傳輸距離的變化， 從圖中可知， 峰值補償后系統的密鑰率和傳輸距離不受系統重復率的影響， 且此時的安全傳輸距離大于不進行峰值補償時的情況.圖5(b)給出了不同傳輸距離L=30，40，50km 的密鑰比特率隨系統重復率的變化， 顯然， 在進行峰值補償后， 系統的密鑰比特率隨系統重復率的增加而呈正比持續增加; 而在不采取峰值補償時， 密鑰比特率隨系統重復率的增加呈現先增加后減小的趨勢.因此， 本文提出的峰值補償方案不僅增加了系統的安全性， 消除了由于有限采樣帶寬引入的安全性漏洞， 也解除了系統重復頻率對密鑰比特率的限制.在計算密鑰率的過程中，涉 及 的 系 統 參 數 分 別 設 置 為VA=20 ，vel= 0.01 ，β=0.95 ，η=0.6 ，fsamp=1 GHz.

4 結 論

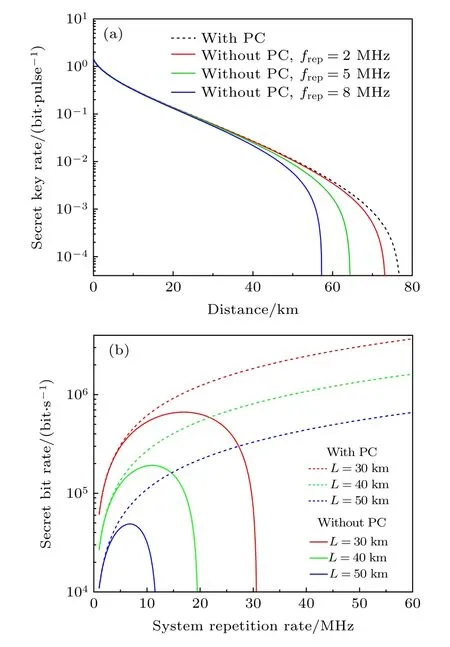
圖5 (a)不同系統重復率下的密鑰率隨傳輸距離的變化;(b)不同傳輸距離下的密鑰比特率隨系統重復率的變化Fig.5.(a) The secret key rate as a function of the transmission distance under different system repetition rate; (b) the secret bit rate as a function of the system repetition rate under different transmission distance.

本文提出了一種基于峰值補償的連續變量量子密鑰分發方案， 通過在接收端的ADC后增加一個峰值補償模塊， 來解決由ADC的有限采樣帶寬引入的安全性問題.詳細介紹了有限采樣帶寬對系統安全性的影響， 描述了峰值補償的具體步驟， 并基于仿真實驗證明了該方案的有效性.此外， 也針對采用峰值補償和不采用峰值補償兩種情況， 分別分析了系統在集體攻擊下的漸近安全性.結果表明， 經過峰值補償后， 系統能正確估計信道過噪聲，從而具有更長的安全傳輸距離， 其密鑰比特率也不再受到系統重復率的限制， 隨重復率的增加而呈正比持續增加.

值得注意的是， 該方案是基于一個脈沖內的三個采樣值來實施峰值補償， 因此ADC的采樣頻率必須大于三倍系統重復率， 這要求系統的重復率不能太高.對目前的CVQKD系統而言， ADC的采樣頻率通常在GHz級別， 而系統重復率通常在MHz級別， 這遠遠滿足三倍重復率的要求.在今后的研究工作中， 會進一步考慮這一要求對系統的影響， 以提高CVQKD系統的性能.