一對多交互式在線客戶服務排隊模型

戴 韜,趙 星

(東華大學 旭日工商管理學院,上海 200051)

隨著移動互聯網技術和社會化媒體的發展,人們悄然改變的溝通習慣已經影響到客服中心,語音熱線來話量逐步下降成為普遍趨勢,企業和客戶之間的聯系不再是以電話交流為主的方式,客戶通過微信、QQ、阿里旺旺等移動即時通訊軟件以在線聊天的方式與企業交流、溝通。相應地,企業傳統的電話呼叫中心升級為以在線溝通為主要渠道的在線客戶服務中心。

從客戶角度,在線客服中心能照顧更多客戶感受：“反應慢”的客戶有了足夠的思考時間,靦腆的客戶有了獨立的提問環境；截屏、語音、文字等溝通方式更多樣,能更快地解決問題；可以根據自身的情形控制溝通的節奏,忙時不用立刻回復；滿足了新生代用戶不喜歡語音交流的緊迫感和某些場合的隱私性要求。從企業角度,在線客服中心提供了更多的便利：效率高、節約人力資源,一名客服人員可以同時服務多名客戶,平均每位坐席可以接待5～15名客戶；在線客服系統可為客戶生動地提供服務選項,給足客戶思考時間,更準確地了解客戶需求,從而做到準確分流,讓服務更細分化；基于移動互聯網的在線客服對硬件及坐席的環境要求較低,可以更加容易地吸引兼職人員進行遠程服務,為自由從業客服和云客服的發展提供了可能。

以排隊論的觀點,在線客服中心與傳統電話客服中心的關鍵區別是客服與顧客間的交互模式發生了根本性改變：一個在線客服可同時為多個顧客提供服務(簡稱“一對多”),而在電話客服中心,一個客服同時僅能為一個客戶提供服務(簡稱“一對一”),如圖1所示。

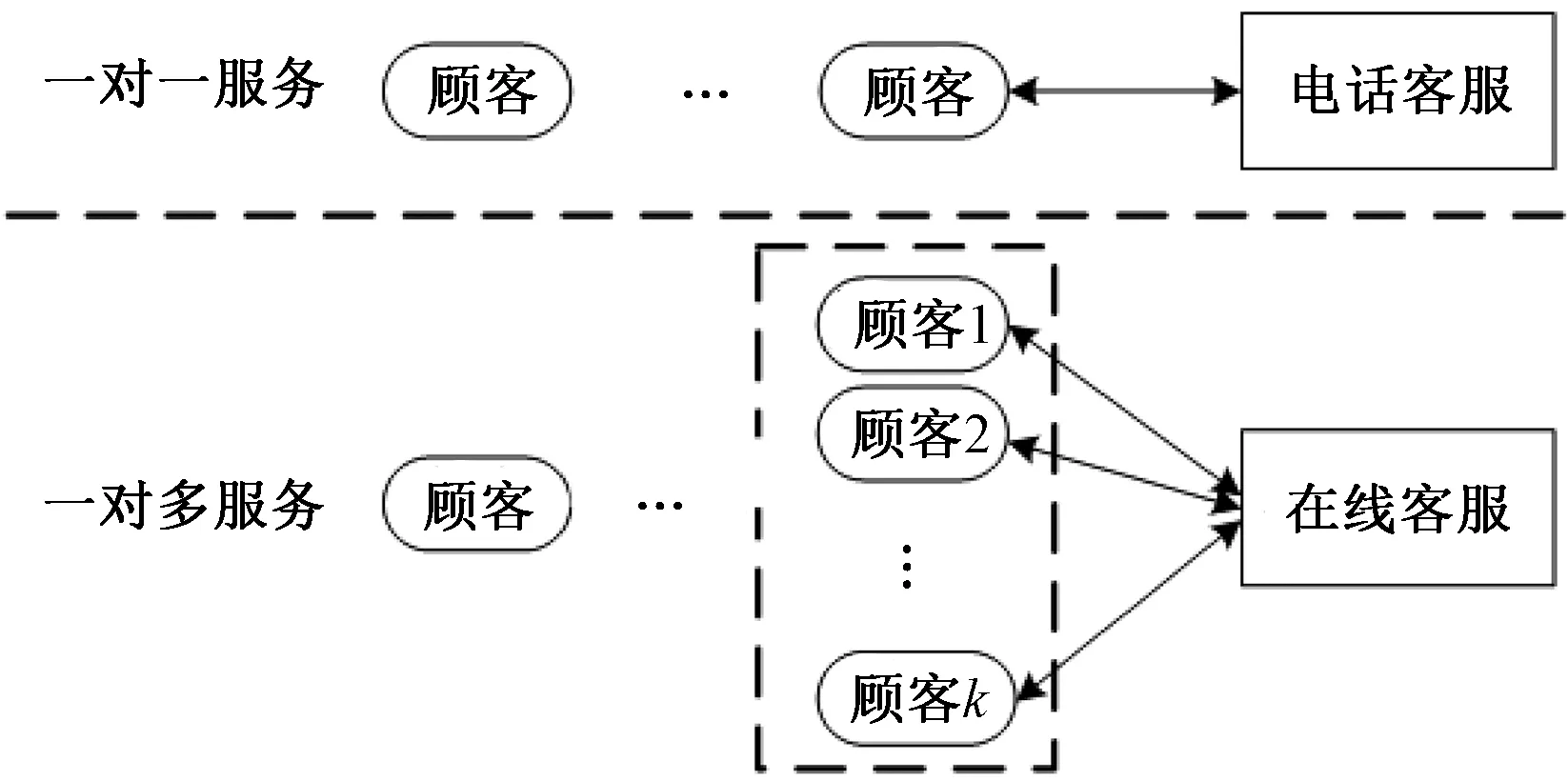
圖1 兩種服務模式對比

與傳統客服中心一樣,顧客的服務滿意度與員工的工作滿意度都影響著企業的服務拓展與運營績效[1],因此,運營經理需要平衡顧客服務水平(一般用顧客的平均等待時間來衡量)與運營成本(員工的繁忙程度)之間的矛盾,將客戶需求量轉化為客服人員需求量是在線客服中心運營的關鍵步驟。基本的排隊論公式是在“一對一”服務模式下推導得出的,無法直接用于在線客服“一對多”的服務模式,故本文分析“一對多”服務模式的排隊特點,提出描述排隊狀況的性能指標,并建立相應的雙層排隊模型來計算指標,為在線客服的運營管理提供理論支撐。

1 文獻綜述

在傳統的客服人力資源配置研究中,各種排隊模型已經被廣泛研究,其基本思路是將顧客到達視為泊松流,各個時段相互獨立且客服服務時間服從負指數分布,Green等[2]將該方法稱為SIPP方法。在SIPP方法假設下,可以采用基于M/M/N的Erlang-C公式計算在滿足一定服務水平下所需的客服人數。吳佳驥等[3]在求解多技能呼叫中心人力需求時,利用經典的Erlang-C 模型求出各技能在各個時段的人力需求。雖然Erlang-C公式是目前在客服中心中應用最廣泛的,但大量的文獻也提到該模型存在的諸多局限性,如顧客不愿意等待而離開,不同時段之間有相關性等。Yom-Tov等[4]分析了顧客重復進入系統的Erlang-R模型。Jouini等[5]對有等待信息告知、多等級顧客以及顧客耐心有限的服務排隊過程構建了相應的模型,并提出了基于馬爾科夫鏈的預計等待時間的估計方法。于淼等[6]研究了帶有排隊信息提示的M/M/N+M排隊模型,給出了穩態系統下的性能指標計算公式,并設計了基于二分法和固定點法的求解方法。

綜合現有研究不難發現,經典的Erlang-C 模型以及相關的衍生排隊模型都基于客服與顧客間“一對一”的交互模式。在線客服與顧客“一對多”的交互模式下,單個顧客在得到客服的一次回復后可能繼續留在系統并發出下一條咨詢,每個客服在回復完一條咨詢后會繼續回復其他顧客的咨詢。因此,在“一對多”的交互模式下的排隊問題不再是標準的排隊問題,也無法使用現有“一對一”模式下的排隊模型。目前,在線客服的相關研究主要集中于服務模式及服務質量的定性分析：萬君等[7]對電子商務網站在線客服彈出窗口對用戶行為的干擾問題做了實證分析；劉順忠[8]利用實證分析研究了網絡購物中顧客購買意向受在線客服溝通方式和商品特征的影響機制。

國內有少量研究將排隊論和在線客服相結合：江小云[9]為了確定合理的客服數量將M/M/C/∞/∞排隊理論應用于網絡實時溝通服務系統；吳賢佑[10]在對某在線客服系統優化時將M/M/C/∞排隊模型應用到系統中來求解系統的性能指標。但這種不考慮客服與顧客“一對多”的交互模式而直接簡化為標準的排隊模型,導致計算出的服務水平和真實的服務水平存在較大差距,嚴重影響最終客服排班結果的準確性,本文3.2節仿真結果也證明了這一點。還有學者對在線客服的新特點下的運營問題展開了研究：Luo等[13]研究了不考慮顧客的不耐煩性,如何配置最優數量的在線客服人員數量；Tezcan等[14]在Luo等的基礎上進行了研究,將模型成果擴展到存在不耐煩顧客的場景。與本文相比,這兩篇文章的重點是在線客服的人員數量配置,為了實現其研究目的,兩篇文章都將其中的基礎因素——單個坐席對不同數量顧客的服務速度作為已知參數。然而,現實中的客服中心僅能夠已知客服回復單條消息的速度,其表現出的服務速率是跟客服與顧客的回復速度及顧客數量等有關的函數,而關于這個函數的具體解析式,這兩篇論文均未討論。Legros等[15]也研究了在線客服的運營問題,其主要關注點是當坐席人員數量確定時,如何在不同坐席之間進行客戶需求的分配。與本文最為相近的是Campello等[16]的研究,他們將醫療服務、在線客服與社區咨詢等排隊問題均抽象為基于“Case Manager”的排隊模型,并提出了主要排隊指標的解析公式,本文與其最大不同是排隊對長與排隊時間的計算邏輯,具體比較詳見3.3節。

綜上所述,比起大量的“一對一”排隊的研究,“一對多”排隊模式下的研究較少,少數的研究也因為關注點的不同,對于最基礎的單客服排隊模型反而缺少深入研究。因此,本文根據現實有可能直接獲取的參數作為已知參數,并提出該模式下的關鍵排隊指標,通過建立雙層排隊模型推導關鍵指標的解析公式。最后,通過與仿真結果的對比驗證解析公式的準確性。

2 排隊模型及解析公式

本文研究一個客服人員服務多個顧客的基礎模型,實際中N個客服的問題既可以近似地將顧客平均分配給各個客服,變成N個互相獨立的“一對多”基礎模型,也可以在本文的基礎模型上,考慮不同的負載之上的客服服務速率,實現最優的人員配置與負載分配[13-15]。因此,單服務臺的“一對多”排隊模型是在線客服的運營優化的基礎模型。

2.1 符號設定

參考文獻中對顧客到達時間和客服服務時間分布的研究[11-12],以及總結了天貓平臺上多個店鋪使用旺旺工具對顧客提供服務的實際場景。對在線客服服務過程的相關參數做出如下假設：

(1)顧客到達是一個參數為λ的泊松過程,其間隔時間服從均值為1/λ的指數分布。

(2)顧客發出每條咨詢消息所需時間服從均值為θ的指數分布。

(3)客服回復顧客每條消息所需時間服從均值為μ的指數分布。

(4)考慮到客服回復壓力以及回復質量,客服最大同時接待的人數為k,系統中的顧客總數超過k人后,顧客進入一個容量無限的空間進行排隊,并根據FCFS的原則,如果一旦有一個顧客完成服務,隊列中排在最前面的顧客進入到服務隊列中與其他k-1個顧客同時接受客服服務。

(5)顧客咨詢i條的概率為p(i),則顧客平均咨詢條數的期望為：E[I]=∑ip(i)=A。極端情況,如果系統中只有1個顧客,客服進行“一對一”服務,則平均總服務時間為

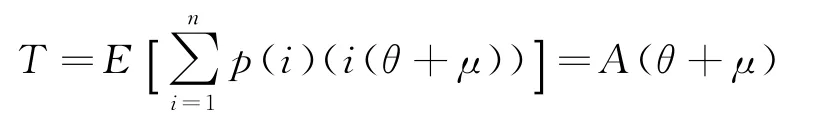
(6)顧客與客服之間是嚴格的“一來一往”交互過程,即一方只有收到對方的應答消息后才會繼續回復。

(7)顧客喜歡在線客服的原因之一是其沒有電話客服中的緊迫感,能夠在處理其他事務的同時進行相關咨詢,所以大部分顧客對在線客服的回復速率有較為寬容的期待,即顧客的耐心指數較高。為了簡化問題,關注其他重要因素,假設顧客能在系統中耐心等待,不考慮顧客的中途放棄。這是符合顧客到達率較小的實際情況的,而對于顧客到達率較大的情況,將其作為系統的平穩條件進行考慮。

上述(2)、(3)和(5)的設定是本文與文獻[13-14]的最大不同。因為根據本文對實際在線客服中心的調研分析,現實中能直接獲得的與服務速率相關的參數僅僅是客服回復單條消息的時間分布,最后表現出的客服服務速率(單位時間服務的顧客人數)跟顧客的單條消息回復速度及顧客與客服之間的交互次數、當時的顧客數量等因素有關,所以不能簡單地給出不同顧客數量下客服的服務速率,否則既掩蓋了一些關鍵的變動性質,在實際應用中也是比較難測定的。

2.2 模型構建

在線客服工作時,顧客通過發送文字消息的方式跟客服人員進行溝通,顧客需要一定的時間來輸入消息(服從均值為θ的指數分布),顧客等待發生在兩個階段：①剛剛到達時等待被接入到合適的客服；②在與客服溝通的交互過程中,顧客發出了消息等待客服回復。顧客通過在整個服務過程中等待時間的長短,衡量本次服務在響應性維度上的滿意度。因此,傳統的排隊模型中的排隊隊長和等待時間兩個指標不足以描述在線客服的排隊狀況,而本文則以完成整個咨詢服務的時間和顧客發出消息后收到客服的平均等待時間來評價系統的績效。

雖然從表面上看,一個客服可以服務多個顧客,但在任何一個時間點上,每個客服只能回復一個顧客的消息(類似于操作系統中CPU 服務各個進程的并發運行),因此,顧客已發出的待回復消息可以抽象為等待的“一對一”單服務臺排隊隊列,每一位顧客只會在其所有問題咨詢完后再離開。根據此特點,將在線客服的排隊模型分為消息層模型和顧客層模型,雙層模型的邏輯圖如圖2所示。

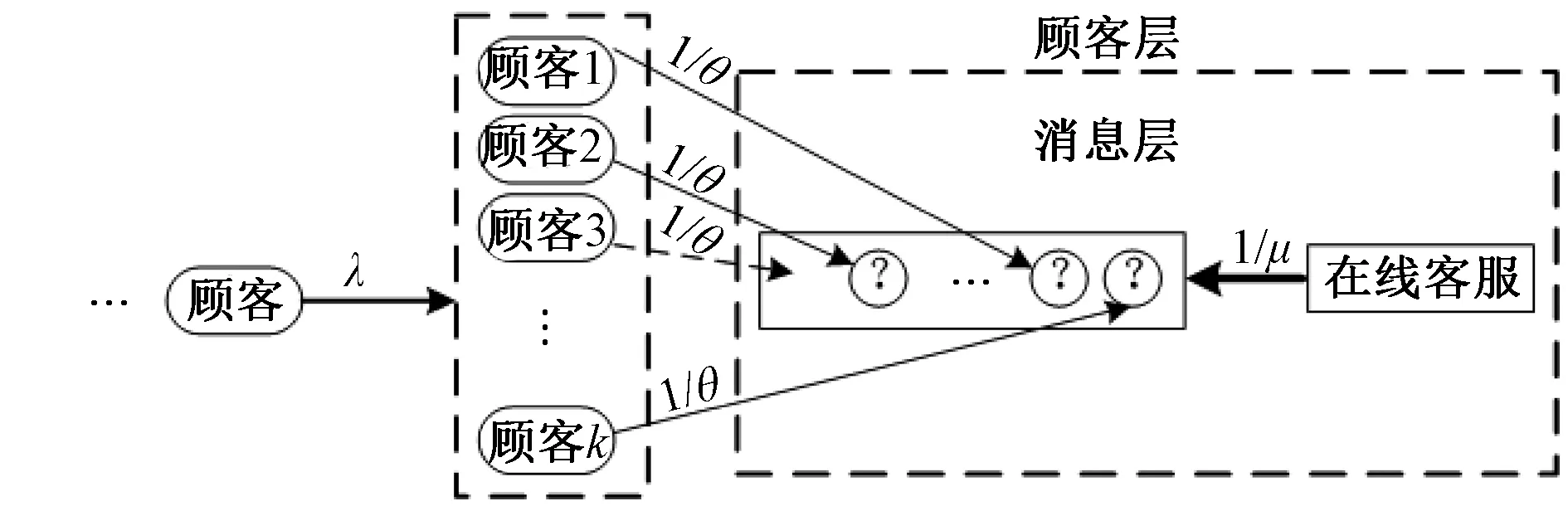
圖2 在線客服雙層排隊模型邏輯圖

其中,消息層模型是確定客服在同時接待m個顧客時,即沒有新顧客到達和離開的假定下,顧客的每條咨詢在得到客服的回復之前的平均等待時間,進而確定在客服同時接待m個顧客時,顧客在系統的平均逗留時間。顧客平均逗留時間將用作顧客層模型的服務速率的計算,同時在顧客層模型考慮客服的最大同時接待能力,最終推導出“一對多”交互模式下排隊模型的相關性能指標。本文提出的雙層模型的最大優點是將一個“一對多”的排隊問題拆分為兩個層次上的排隊問題,而這兩個層次上的排隊都是“一對一”模式的,這樣就可以用典型的生滅過程來描述其狀態變化過程,較容易進行排隊公式的推導。

2.3 消息層排隊模型

因為系統中有m個顧客,所以等待客服回復的消息條數為0～m條之間,假定某時刻系統有i條消息待客服回復,則剩余m-i個顧客發出消息的速率為(m-i)/θ,此時的系統可近似為單服務臺顧客源有限的排隊模型[17],記為M/M/1/m/m,其穩態系統的狀態轉移圖如圖3所示。

圖3 消息層模型狀態轉移圖

圖3中的狀態p(i)表示消息隊列中有i條消息待回復的概率,根據狀態轉移圖可以列出如下K氏方程：

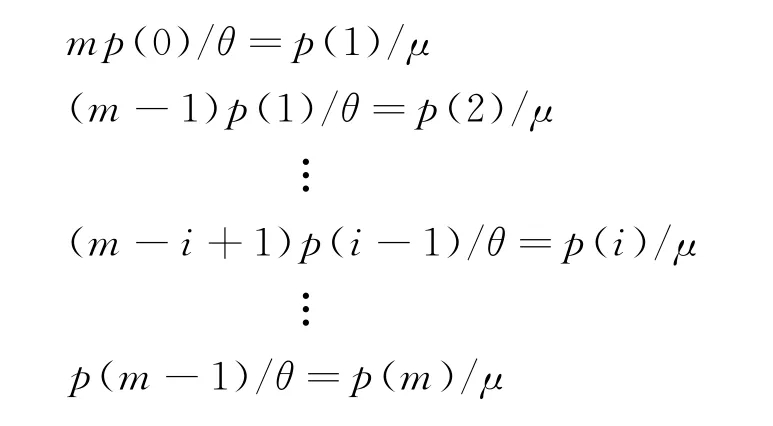
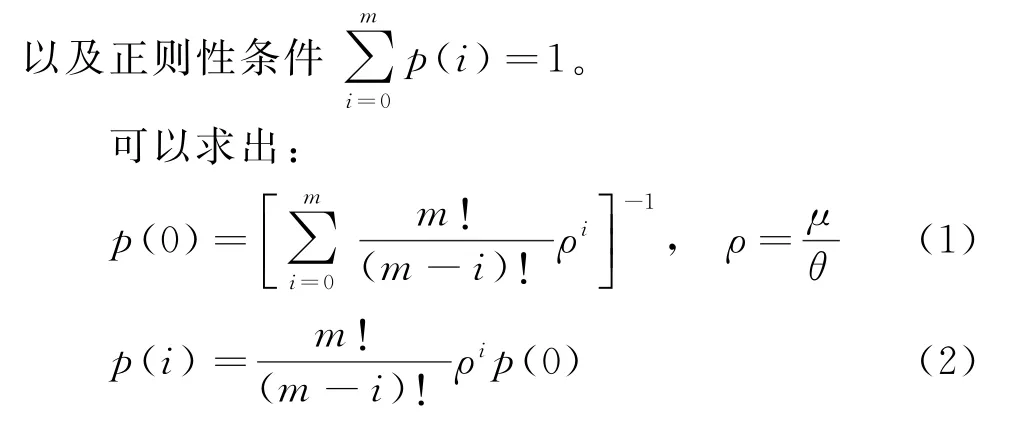
令c為系統中總的平均待客服回復的消息條數,則還未發出消息的顧客為m-c人,記新消息的到達速率為有效到達率,即

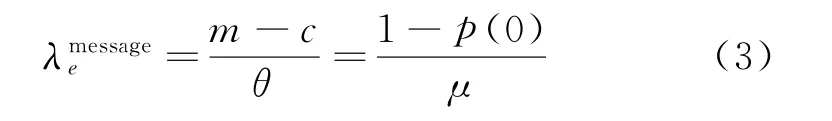
系統中等待客服回復的平均咨詢條數為

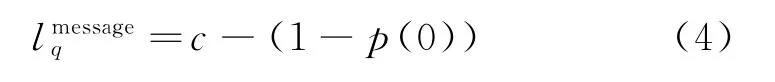
結合式(3)可得

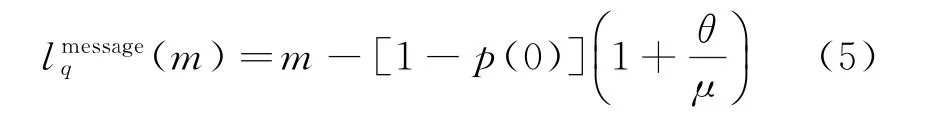
因此,根據Little’s Law,可以得到當系統中有m個顧客時,顧客每條咨詢被回復需要的平均等待時間為

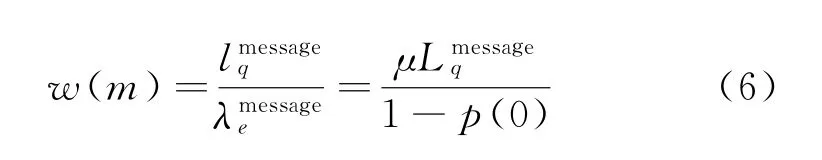
將式(5)代入式(6),得

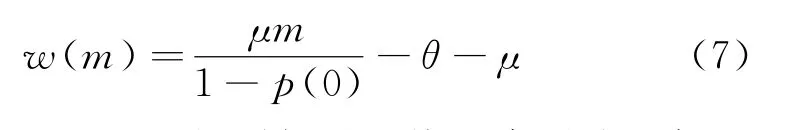
根據式(7),可以得到如果系統一直平穩地保證剛好有m個顧客,每個顧客在系統中平均逗留時間為

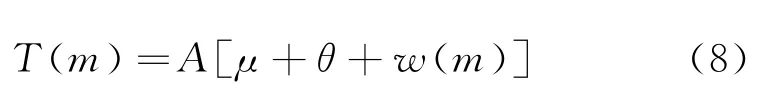
2.4 顧客層排隊模型

2.3 節中顧客的平均服務時間T(m)是在系統中剛好有m個顧客的假設下得到的,從整個客服接待過程看,客服接待的人數會隨著新顧客到達和顧客接受完服務離開系統而不斷變化,故需將2.3節得到的消息層平均服務時間T(m)引入到第2層排隊網絡中,繼續考慮顧客人數不斷變化的顧客層排隊模型。

考慮最一般化的在線客服系統,假定該系統的最大容量為n,客服最大同時可接待人數為k,顧客到達系統的到達率為λ。當系統中顧客人數m＜k時,客服服務速率為m/T(m)；當m＞k時,剩余部分顧客耐心等待,系統的服務速率為各階段狀態轉移圖如圖4所示。

圖4 顧客層狀態轉移圖

圖4描述的是顧客無限到達的變服務速率的排隊過程,為了方便求出各個狀態的概率pp(i),進而求出總的服務時間,將k～n狀態視為子過程1,該過程的各狀態下,客服均全負荷工作,服務速率保持不變,各個狀態的概率分別為pp′(k)…pp′(n),根據圖4列出子過程1的k氏方程如下：

結合全過程的正則性條件：

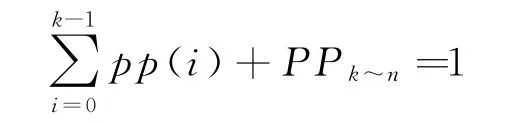
以及全過程中k-1～k狀態的狀態轉移方程

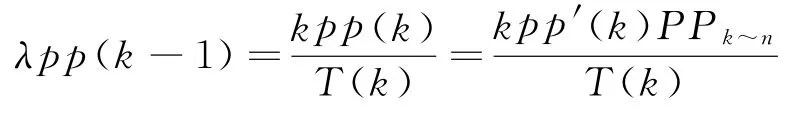
因此可求得

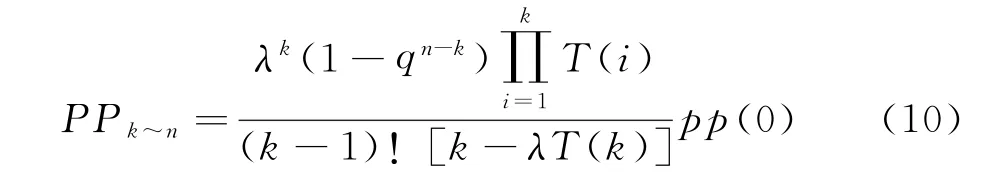
式中,

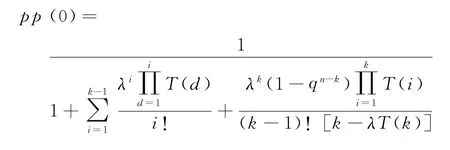
全過程各狀態概率為當i≥k時：

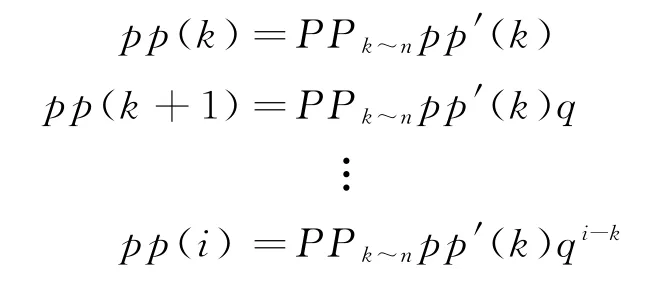
當i＜k時,

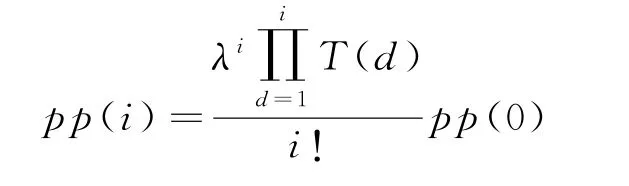
可得到在系統顧客人數不斷變動的情況下,顧客平均逗留時間為

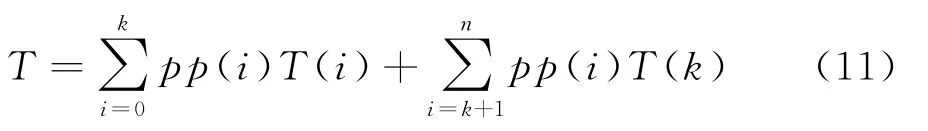
系統中平均顧客人數即系統平均隊長為

系統中顧客平均等待回復時間為

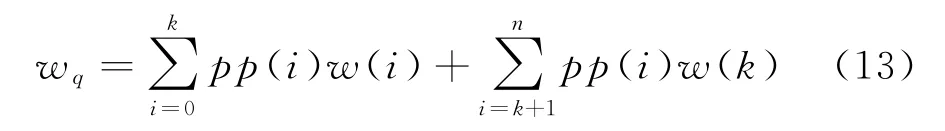
由此,可通過雙層模型得到3個關鍵指標,即系統平均逗留時間、系統中平均客戶數量和每條消息平均等待回復時間的解析公式(見式(11)～(13)),其中狀態概率pp(i)由n個獨立的方程組確定。在實際使用過程中,僅需給出已知參數A、μ、θ、λ、n和k,就可使用常用求解軟件得到關鍵的排隊指標。

因此,在應用模型時,可以將n→∞當作排隊容量有限的特殊情況(事實上,所有的客服中心排隊容量都是有限的),選擇一個較大的n值進行近似即可。如在第3節算例中的情形,當選擇n=20時,在最大穩態保證的到達率下,

即對于n＞20的概率,完全可以忽略不計。

3 數值仿真

本仿真算例的數值來自2016年天貓商城某服裝品牌的旺旺客服數據,本文統計了其16個客服2天的實際數據,得到如下已知參數：顧客發出每條消息所需時間服從θ=50 s的指數分布,客服回復每條消息所需時間服從μ=35 s的指數分布,客服最大接待顧客人數k=10人,系統能接受的顧客總數不限,根據第2節最后的討論,用n=20進行近似,顧客的咨詢條數數學期望A=3.09條。

算例中的方程求解使用Lingo軟件進行,仿真結果通過使用同樣的輸入數據在Flexsim 軟件中建模得到。

3.1 穩態接待能力分析

為了確保系統處于穩態狀態,即在顧客層需要保證q＜1,即λ＜k/T(k),因此可得不同k值(單客服最大服務人數)下,系統能夠接受的最大到達率。

在本算例中,當A、θ和μ這3個參數已知時,k/T(k)即系統能接受的最大到達率,得到最大可接受到達率與最大服務人數之間的關系如圖5所示。

由圖5可知,根據現實的管理要求,該客服中心的單人同時最大的接待人數取k=10,可以得到最大到達率λ=0.009 239 312 人/s,即為了維持穩態系統,需要保證分配給每個客服的顧客到達的平均時間間隔最小為108.2 332 s。

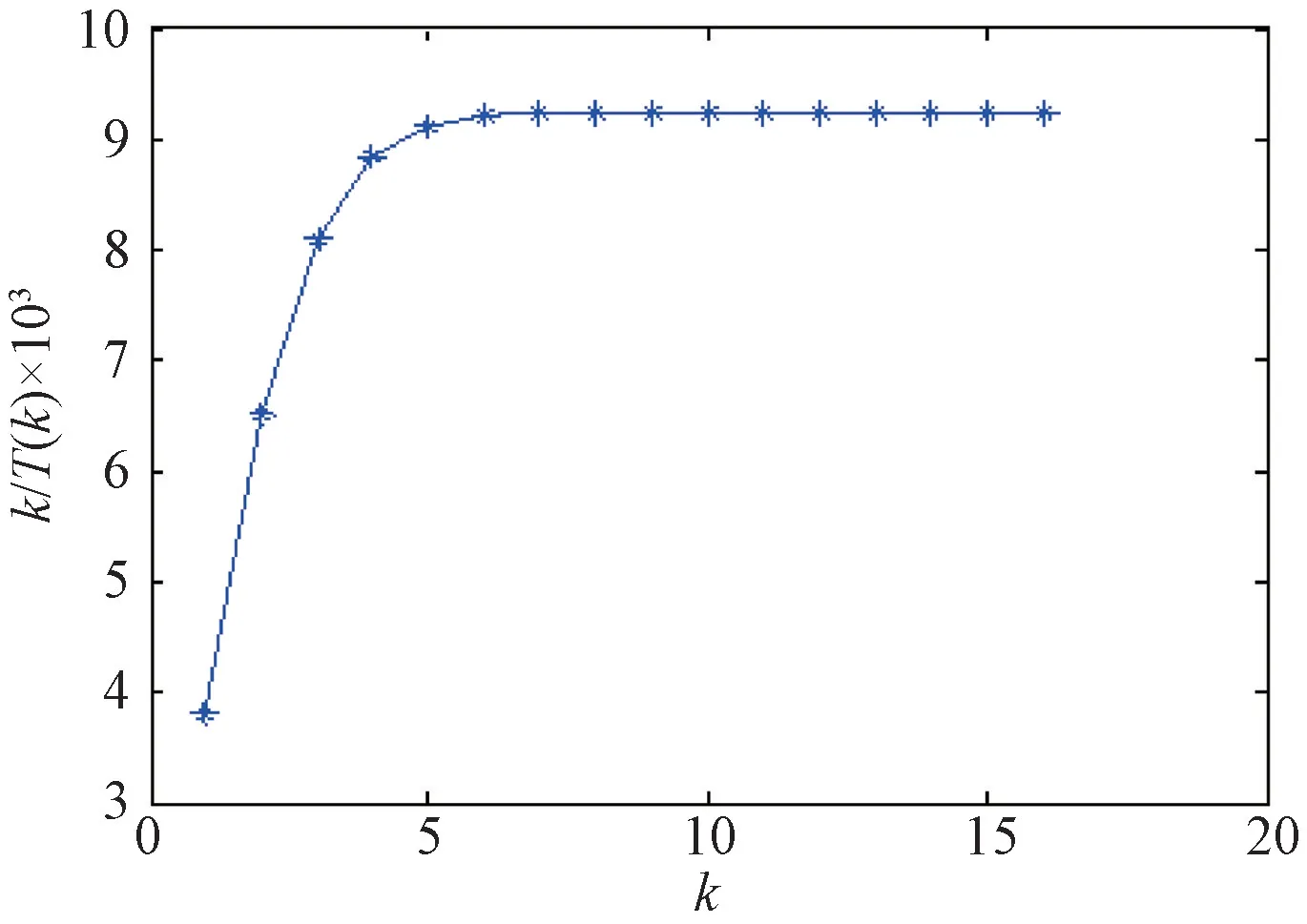
圖5 最大可接受到達率分析

3.2 數值結果對比

為了驗證解析模型的準確性,保證基本運營參數不變,調整顧客到達率λ得到一系列解析公式值和仿真值。其中,顧客到達率的變化區間為[0.004 167,0.01](人/s),即顧客到達平均時間間隔為[100,240](s)。

分別計算第2節提出的3個關鍵排隊指標：平均服務時間、每條消息平均等待回復時間和系統平均客戶數量,數值對比如圖6所示。

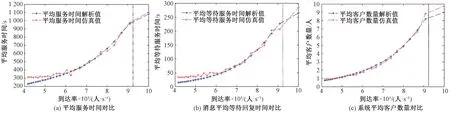
圖6 關鍵排隊指標數值對比圖

分析圖6的結果,當到達率較小時,圖中的虛線左側部分,解析公式值與仿真值均有較好的貼合,其中的誤差是因為解析值僅能給出一個均值,而仿真結果由于是根據參數隨機產生驅動事件,其值會在解析值的上下波動,說明本文構建的雙層排隊模型能僅利用“客服回復消息時間”“顧客回復消息時間”及“顧客的平均交互次數”這3個輸入參數,很好地計算平均服務時間、每條消息平均等待回復時間和系統平均客戶數這3個關鍵指標,并且解析過程的計算時間遠遠小于仿真模型的時間。

算例中的仿真時長設為28 800 s,表示一天中的8 個小時,進行10 次仿真后求平均值得到。Flexsim 軟件的基本運行機理是：根據到達率隨機生成顧客,每個顧客獨立在仿真模型中停留,最后統計得到該到達率下排隊系統的關鍵指標。由于Flexsim 軟件的仿真特性,每次仿真均產生了數目龐大的獨立顧客,使得最后統計值的變動方差比較小,并且,隨著到達率變大,每次仿真產生的獨立顧客數量越多,變動方差更是降低,故仿真值具有“較窄”的置信空間。表1所示為以平均服務時間指標為例,給出了幾個典型到達率下的仿真置信空間。

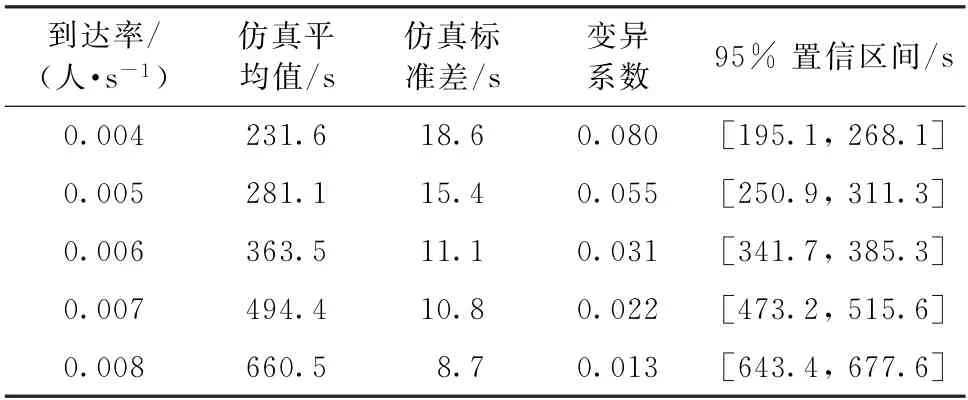
表1 部分典型到達率下平均服務時間仿真值置信區間

解析值與仿真值的主要差距出現在到達率不斷變大的過程中,在圖6中為虛線的右側部分。虛線表示到達率0.009 2個/s,即在給定參數下的系統最大可接受到達率,說明本文提出的模型僅適合應用于穩態系統,當系統處于不穩定狀態(即顧客排隊會無限增長),解析公式的解會急劇惡化。造成該現象的原因是,本文模型在推導中未考慮顧客的不耐煩性,而在現實的排隊過程中,如果因為過高的到達率使得顧客陷入長時間的等待,理性的顧客會選擇中途退出,或者在排隊初期就不會進入咨詢隊列。

3.3 與其他近似模型對比

對于本文關注的在線客服的特別問題,部分學者曾提出可以將“一對多”交互式服務近似為N可變的M/M/N多服務臺排隊模型[10]。本文比較其近似方法與本文模型的效果。

將近似模型的服務速率設置為1/A(μ+θ),考慮不同的顧客到達率下,選取不同的近似服務臺數,計算出相應的平均服務時間,并與本文得到的雙層排隊模型解析解和仿真解進行對比,如圖7所示。

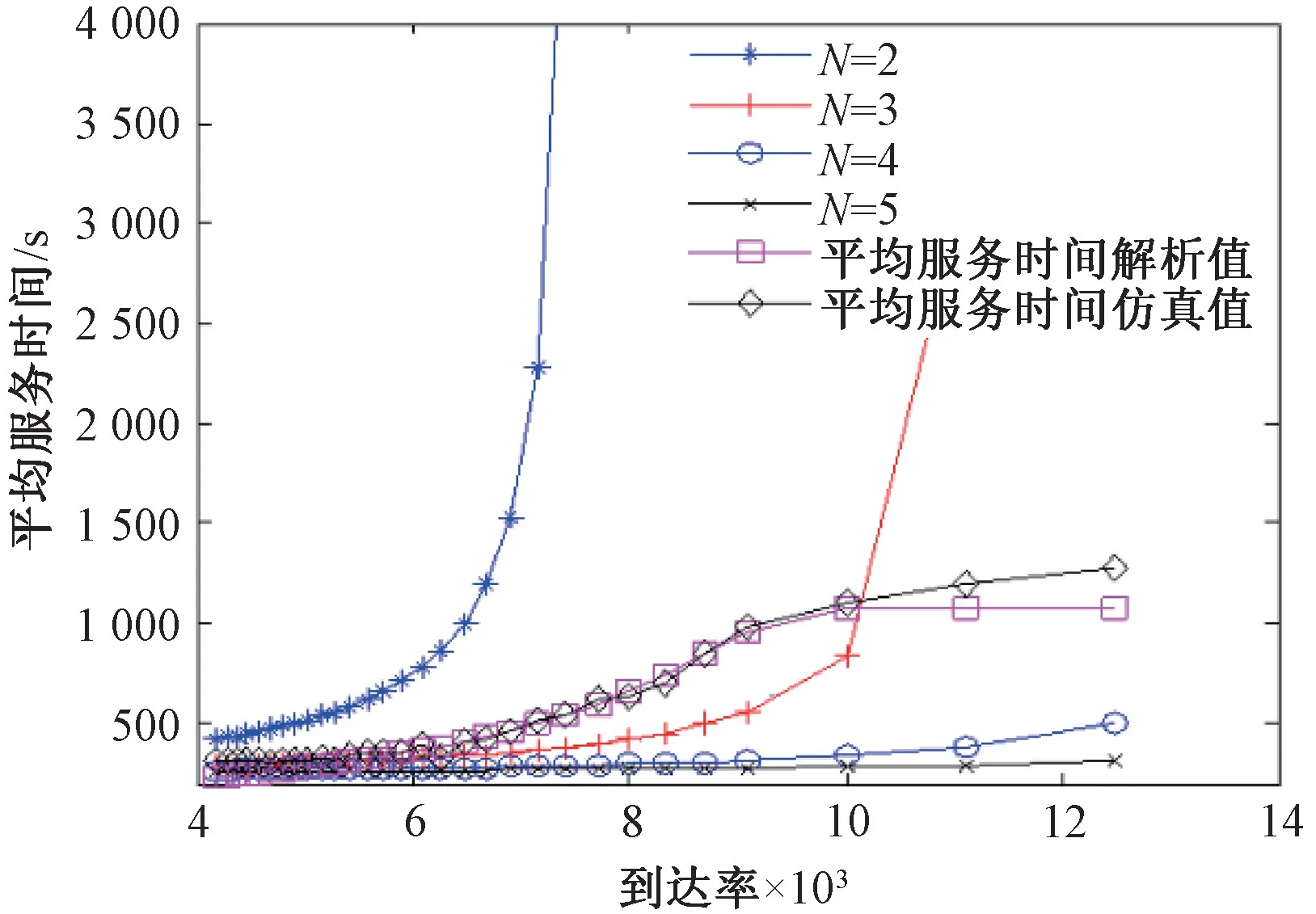
圖7 與M/M/N 排隊模型對比

通過對比發現,隨著N的增加,平均服務時間逐漸趨于定值,但無論N取哪個值,平均總服務時間與仿真模型的結果始終有較大的偏差；而本文提出的雙層模型卻能一直與仿真值較好地貼合,表明利用近似M/M/N模型無法較準確近似“一對多”交互式排隊模型。

Campello模型[16]是與本文最為相近的一個研究,該文提出了多客服“一對多”服務的排隊指標近似模型,根據客戶需求在多客服之間的不同分配原則,提出了T、R、B和P等4個模型,但其研究思路與本文是不同的,他們分別用近似模型計算了開始服務后每一次交互的等待時間(等待消息長度)和客服首次響應前平均等待時間(等待隊伍長度)。

在單客服場景下,Campello等[16]提出的4個模型是完全一致的,其用單服務臺K個有限顧客的排隊近似與客戶之間的交互過程,用客服滿負荷工作速率乘以繁忙程度近似客服實際工作速率,為了獲取繁忙程度的指標,其必須將平均消息條數(No.of visits to server,1/γ)作為已知參數。而本文的思路是,參數1/γ在現實中很難獲取,故可直接將客服與顧客交互過程(消息層排隊)得到的服務速率直接代入顧客層排隊模型進行計算。本文模型與Campello模型在單客服下的結果比較如表2所示,表2中仿真均值的獲得過程與前文一致,其置信區間同表1。

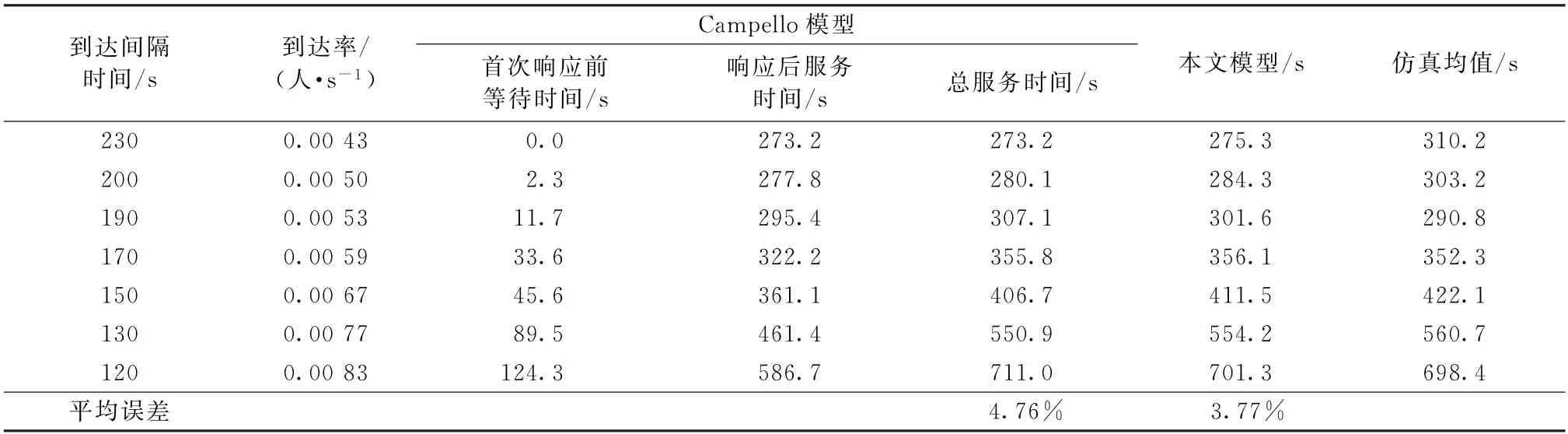
表2 單客服場景下與Campello模型對比結果

通過分析發現,在單客服場景下,雖然Campello模型能分別計算客服首次響應前等待時間和客服首次響應后等待時間,但是由于其做了2次近似,本文模型在平均服務時間指標上的計算準確度上有更大的優勢。

將本文模型在多客服場景下拓展。現實中常以JSC(Join-the-Smallest-Caseload)策略進行多客服之間的工作量分配。JSC策略將新到達的客戶分配給目前工作負荷最輕的客服,以保證每個客服工作量盡量平均,即在同一時刻,最繁忙與最空閑客服的顧客差1人。本文以完全平均的方式近似JSC 策略,即假設顧客完全平均分配在多個客服中。使用Campello等[16]Table 2給出的數據,用本文模型進行計算并與Campello模型進行對比。由于對參數定義的不同,將Campello數據轉化為本文的數據：

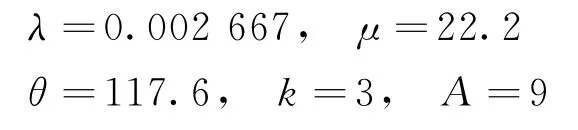
其中,本文模型不需要參數1/γ。對比結果如表3所示。

根據表3,發現本文模型無法單獨計算預分配等待時間和服務中等待時間,而是直接得到了總等待時間。與Campello模型[16]一樣,本文模型的結果也比仿真結果略偏小,本文模型在多客服場景上利用JSC 策略的擴展更接近于Campello 的B 模型,在多客服場景下表現不如Campello模型的原因是,本文假設每個客服的工作量、客戶數量等指標是完全一致的,這在JSC 策略下由于服務速率的不確定性影響,是不可能達到的。因此,如果為了提高本模型擴展到多客服場景下的準確性,需要在路由分配時對每個客服進行獨立計算并匯總。

表3 多客服場景下與Campello模型對比結果

4 結語

本文在對我國在線客服中心實際情況進行抽象假設的基礎上,提出了在線客服中心排隊系統的3個關鍵排隊指標：平均服務時間、消息回復等待時間和系統平均顧客人數,并通過構建兩層排隊模型,將“一對多”服務模式下的排隊問題變成兩個層次上的“一對一”排隊問題,通過生滅過程分析推導了3個關鍵指標的解析公式,同時給出了系統處于穩定狀態的條件。通過將解析值與仿真值及M/M/N 近似模型進行對比,驗證了解析公式的準確性。將本文模型與Campello 模型[16]對比發現,雖然Campello模型能應用于多客服的排隊績效計算,并且其模型能分別給出進入服務前等待時間與開始服務后的系統逗留時間,但是在單客服的場景下,本文模型得到的平均服務時間指標更加準確,且無需已知平均消息條數。而在多客服的場景下,本文模型的簡單擴展不如Campello模型準確。因此,在以本文模型為基礎進行多客服場景的擴展時,需要獨立計算每個客服的排隊指標再進行匯總,本文模型對于更加準確地計算在線客服中心的排隊績效是有理論與實際意義的。