地埋垃圾站縱梁彎曲變形分析

向 偉，馮子剛，胡興新，趙佳樂，岳凱凱，曾繁榮

（重慶科技學院，重慶 401331）

0 引言

相比于傳統地面垃圾站，地埋式垃圾站有著更好的環境效益與經濟效益。在科技進步、人們對生活質量要求越來越高的現在，地埋式垃圾站將成為環衛行業的一重要發展方向，而其中縱梁又在地埋站內起著支撐及運移垃圾車箱的重要作用。

某地埋式垃圾站內的縱梁在自身桁架結構及壓縮機和垃圾車廂的力學作用下，產生了彈性變形，且梁上垃圾車廂在轉移過程中由于沖擊或振動會引起縱梁共振，造成疲勞破壞。考慮到縱梁在地埋垃圾站中的重要性，有必要對其正常工作時的應力應變分析及模態進行分析。

1 縱梁基本受力情況

1.1 力學模型簡化

在地埋垃圾站中縱梁主要起到支撐作用，整體結構主要由兩根材料為Q345 的背對背22 號槽鋼和中間焊接的橫向同型號槽鋼組成。在實際情況中，縱梁通過立柱支撐著地埋站的整體桁架結構，導軌上放置垃圾車箱，縱梁兩端下方有兩根支撐橫梁。工作時轉運垃圾箱的勾臂車會將車箱勾起，車箱后輪沿著導軌滾動，直至車箱拖離縱梁。

縱梁正常工作時一般只承受靜壓力，只有在垃圾裝滿、車箱運移時才涉及動力學理論。為了簡化縱梁的力學模型，主要針對縱梁跨中承受車箱重量時進行力學分析，因此可將縱梁考慮成普通簡支梁分析其受力狀況。當垃圾車廂位于跨中時簡化后的模型如圖1 所示。

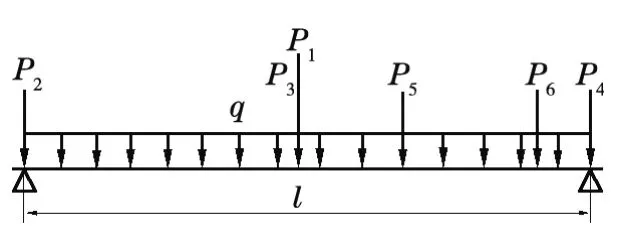
圖1 簡化后縱梁力學模型

其中，P1為垃圾車廂在縱梁上的重力，為55 000 N，方向豎直向下；P2、P3、P4為縱梁上方架構所作用的重力，均為3300 N，方向豎直向下；P5、P6為垃圾壓縮機的重力，均為7500 N，方向豎直向下；q為縱梁自身重量產生的均布載荷，為1364.5 Pa；l 為縱梁理論跨度，長度為6000 mm。

1.2 縱梁彎曲變形基本理論計算

根據縱梁受力的實際情況來看，在滿足胡克定律的情況下可采用疊加法計算縱梁的彎曲變形[1]。在縱梁的簡化模型中，縱梁主要受均布載荷和集中載荷的作用。

有均布載荷撓度計算公式[2]：

式中 ω——撓度

q——均布載荷，Pa

l——縱梁跨度，mm

E——材料彈性模量

I——截面慣性矩

不位于跨中的集中載荷的撓度計算公式：

式中 P——集中載荷，N

b——集中載荷與右端點距離，mm

x1——所計算撓度產生位置，mm

經計算后各均布載荷及產生的撓度的絕對值為ωq=0.82 mm，ωP1=8.83 mm，ωP3=0.53 mm，ωP5=0.98 mm，ωP6=0.25 mm。則總彈性形變的理論值由疊加法算得ω總=11.41 mm。

在縱梁彈性形變基本理論計算過程中，采用的是簡化后的簡支梁模型，沒有考慮縱梁的具體結構組成。根據實際情況來看，縱梁中間的槽鋼能夠增大縱梁的截面慣性矩，因此理論計算值應大于實際值。

從現場測量的結果來看，跨中位置彎曲變形量為6 mm，小于理論計算值，符合實際情況。同時也說明，可以通過增加縱梁關鍵部位的截面慣性矩，從而增強縱梁的抗彎剛度，提升縱梁的整體抗彎性能。為進一步驗證縱梁的變形情況和固有頻率，還應該對實際的縱梁結構進行有限元分析。

2 縱梁有限元分析

2.1 三維模型建立

縱梁的三維模型是通過三維建模軟件Inventor 建立的，包括其整體的兩根縱向的22 號槽鋼結構以及中間間隔布置的橫向同型號槽鋼，槽鋼上方有鋼板和小車的移運軌道。

2.2 有限元網格劃分

縱梁的有限元分析工作采用ANSYS 軟件下的子軟件Workbench 進行分析，將三維模型導入到軟件中的Static structural 模塊后，從軟件得材料庫中選擇縱梁材料為Q345，隨即對縱梁的模型進行網格劃分。針對縱梁較為復雜的幾何結構，采用適應性較好的自由網格劃分方法對縱梁進行網格劃分，能夠保證網格的整體精度質量，使求解結果盡量準確[3]。劃分完成的整個模型的單元為253 433 個，節點數為496 957 個。

2.3 約束及載荷的施加

根據實際情況，縱梁下方放置于站底橫梁上方，所以對縱梁下方于底橫梁的接觸表面施加固定約束。

縱梁受到的整體框架結構的重力，由3 根支柱作用到縱梁上方，每處大小均為3300 N，方向豎直朝下，即載荷A、載荷B、載荷C。同時，垃圾壓縮機的重力同樣通過另外的支柱作用于縱梁上，每處大小均為7500 N，方向豎直朝下，即載荷D 和載荷E。載荷F 為垃圾車廂作用在縱梁軌道跨中時的重量，大小為55 000 N，方向豎直向下。

2.4 有限元分析結果

縱梁的最大等效應變發生在縱梁跨中軌道下方槽鋼處，為4.93 mm，縱梁跨中的應力為150 MPa，而最大等效應力為280 MPa，位于縱梁下方與橫梁接觸處。這是由于縱梁施加固定約束是將固定約束部分當做剛體不能退讓，所以會使得縱梁向下彎曲變形時約束區域自身的邊緣產生擠壓，因此容易產生應力集中。事實上，在各個載荷的作用下，縱梁產生最大應力與應變的位置應處于縱梁的跨中。從跨中的應力應變結果來看，縱梁材料Q345 的強度滿足需求，符合實際情況。

靜力學分析的結果表明，雖然縱梁在垃圾車箱處于跨中時會產生彈性變形，但跨中產生的最大應力值仍在縱梁材料的允許范圍內。

3 縱梁模態分析

有限元模態分析能夠計算出縱梁的固有頻率和固有振型，了解縱梁的固有振動頻率，不僅能夠預防其受到垃圾車廂沖擊而產生共振引起的疲勞破壞，還可以盡量避免或減小工作時縱梁受到的影響，延長縱梁的使用壽命。

（1）縱梁的1 階模態固有振型反映了縱梁的橫向收縮振動，頻率為37.85 Hz；2 階固有振型反映了縱梁的垂向彎曲振動，頻率為40.49 Hz。

（2）縱梁的3 階模態固有振型反映了縱梁的扭轉振動，頻率為95.83 Hz；4 階固有振型反映了縱梁的2 階垂直彎曲振動，頻率為103.53 Hz。

（3）縱梁的5 階模態固有振型反映了縱梁的橫向扭轉拉伸振動，頻率為115.13 Hz；6 階固有振型反映了縱梁的局部拉伸振動，頻率為149.84 Hz。

模態分析結果得到了縱梁各階的固有頻率，所以在實際工作時，操作人員應盡量避免車箱運移時，垃圾車箱輪子滾動產生相近頻率的振動，防止引發縱梁共振、造成縱梁疲勞破壞，進而延長縱梁的使用壽命。

4 結論

（1）通過理論計算與有限元應力分析，得到縱梁的應力與應變狀態，由疊加法計算和有限元分析的結果顯示，在最大撓度的跨中地方縱梁所受應力滿足材料強度要求。針對出現的縱梁應力集中的兩端與坑底橫梁接觸的地方，可以適當增加縱梁截面積，增加縱梁截面慣性矩，增強縱梁的抗彎性能，如可通過加腹板的方式增加局部強度等。

（2）通過有限元模態分析，得到了引起縱梁共振的各階頻率大小，為了盡量避免環衛工作人員轉運垃圾車箱的操作過程中引發縱梁共振，在后續應該進行進一步進行試驗研究，測量和驗證車箱在不同拖移速度下的激勵振動對實際縱梁各階頻率的響應結果。

總體來說，本次針對縱梁的靜力學分析計算與模態分析，可以為今后縱梁的結構優化設計提供理論基礎和依據。