基于改進全階滑模觀測器變頻空調電動機轉速辨識研究*

珠海格力電器股份有限公司 陳萬興 梅正茂 方小斌 唐海洋

0 引言

相比傳統空調用電動機運行抖振頻率±3.0 Hz滿足恒溫調濕要求，變頻空調在降低出風含濕量的同時控制出風溫度，其方案如圖1所示。相比于風冷散熱，風冷和水冷散熱相配合可減小冷凝換熱溫差，從而達到降低系統冷凝溫度的目的，提高性能系數，全工況滿足出風含濕量≤8.0 g/kg、溫度16～30 ℃可調。變頻電動機調節制冷劑流量，按需輸入除濕量，雙冷凝器并聯，通過雙電子膨脹閥調節制冷劑流量配比，按需輸出再熱量，減少機組能耗，因此電動機運行抖振頻率精度嚴重制約高效恒溫除濕性能。

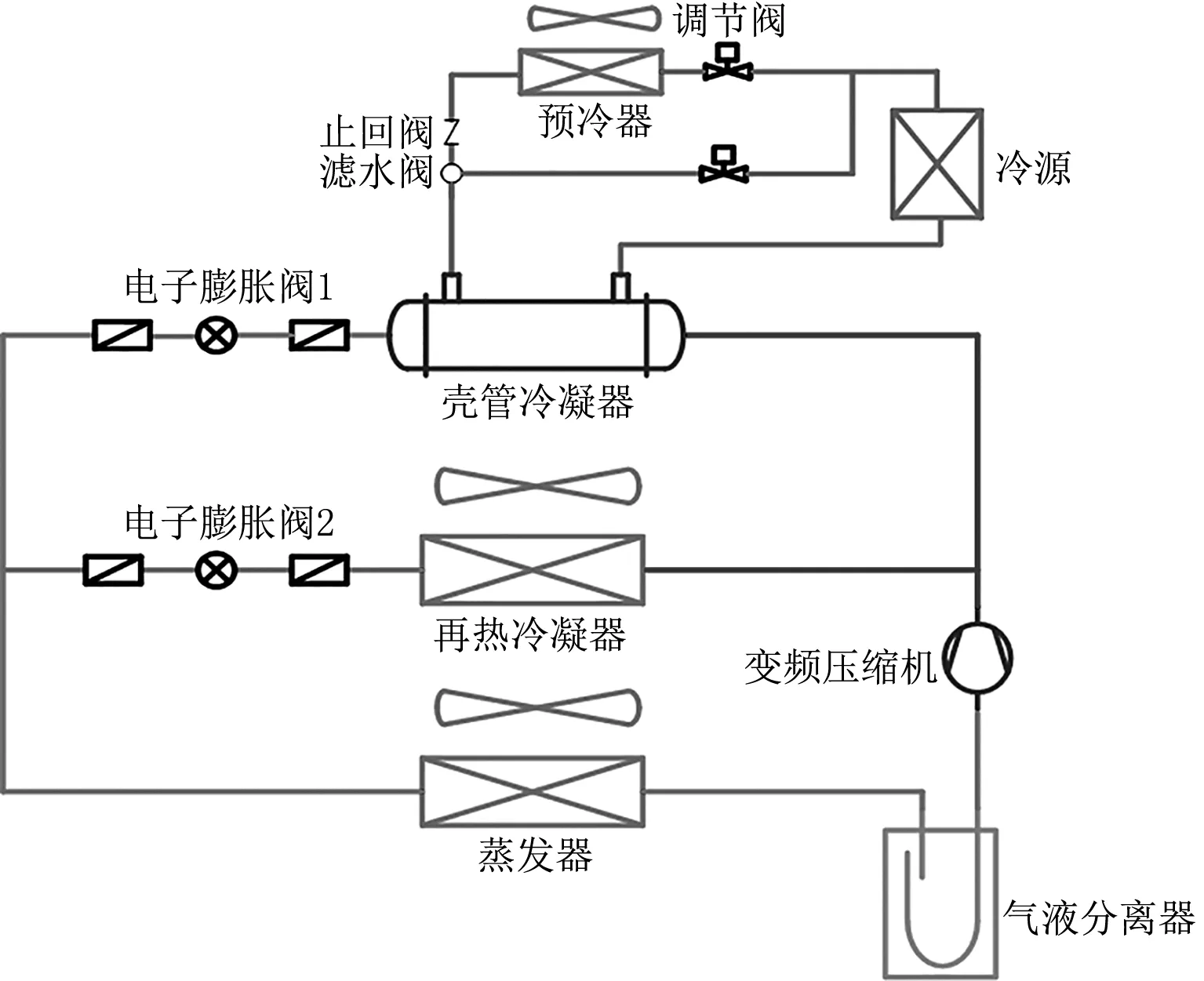
圖1 變頻空調雙冷源水冷方案

為了減小變頻空調頻率抖振幅度，提升電動機轉子頻率精度，精準控制新風出風溫度和含濕量。在常用運行轉速時，滿足變頻風機轉頻的2～8次諧波頻率不落在風機的固有頻率上，風機轉速2 600 r/min，離心風機轉頻43.32 Hz，葉頻(葉片數×轉頻)216.51 Hz，結構七階模態頻率249.39 Hz的要求。

本文分析了傳統的滑模觀測器方程，引入反電動勢作為狀態變量，構建了全階滑模觀測器，分析反電動勢的狀態表達，去除了低通濾波器環節，避免濾波器帶來的相位延遲和補償不準確的問題。構建變增益的切換函數，改善了系統抖振問題。實驗表明，本文所提出的方案可以更準確地辨識電動機位置，轉速辨識具有較好的穩態特性。實現頻率精度控制在0.2 Hz以內，保證其運行時的高效恒溫除濕性能。

1 傳統滑模觀測器速度辨識問題分析

通過滑模觀測器的觀測電流和實際測量電流構建滑模面，經過濾波處理后得到反電動勢，再由反電動勢計算出電動機位置和轉速，代替速度傳感器。

根據永磁同步電動機的數學建模方程，可以列出在靜止坐標系下電動機的電壓方程：

(1)

式中U、E分別為定子電壓和反電動勢電壓，V；Rs為定子電阻，Ω；p為微分因子；L為定子電感，mH；ωe為轉速，r/s；I為電流，A；下標α、β、d、q分別代表α軸、β軸、d軸和q軸。

可以得到反電動勢的表達式：

(2)

式中θe為轉子角度，°；Eex為反電動勢幅值，V。

根據式(1)、(2)可以得到以電流為狀態變量的狀態方程：

(3)

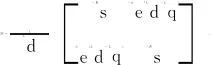
Z為由滑模面估算的反電動勢，其表達式如下：

(4)

按照式(3)、(4)構建的滑模觀測器系統如圖2所示。

圖2 反電動勢觀測器

(5)

(6)

滑模觀測器結構簡單、魯棒性強、系統易收斂，但是傳統的切換函數滑模面存在高頻抖動的問題，因此，在觀測的反電動勢上需要增加低通濾波器，通過觀測轉速去補償低通濾波器帶來的相位延遲。電流誤差開關量中包含了相對較低頻率的反電動勢信號，但同時包含了開關函數引起的高頻切換信號，所以需要將這部分高頻信號濾除掉，只保留有用的反電動勢信號，可以選擇使用低通濾波器來實現。低通濾波器的傳遞函數如下式所示：

(7)

式中s為拉普拉斯算子；ωc為低通濾波器的截止角頻率。

2 全階滑模觀測器設計

2.1 全階滑模觀測器狀態方程

全階滑模觀測器系統如圖3所示。

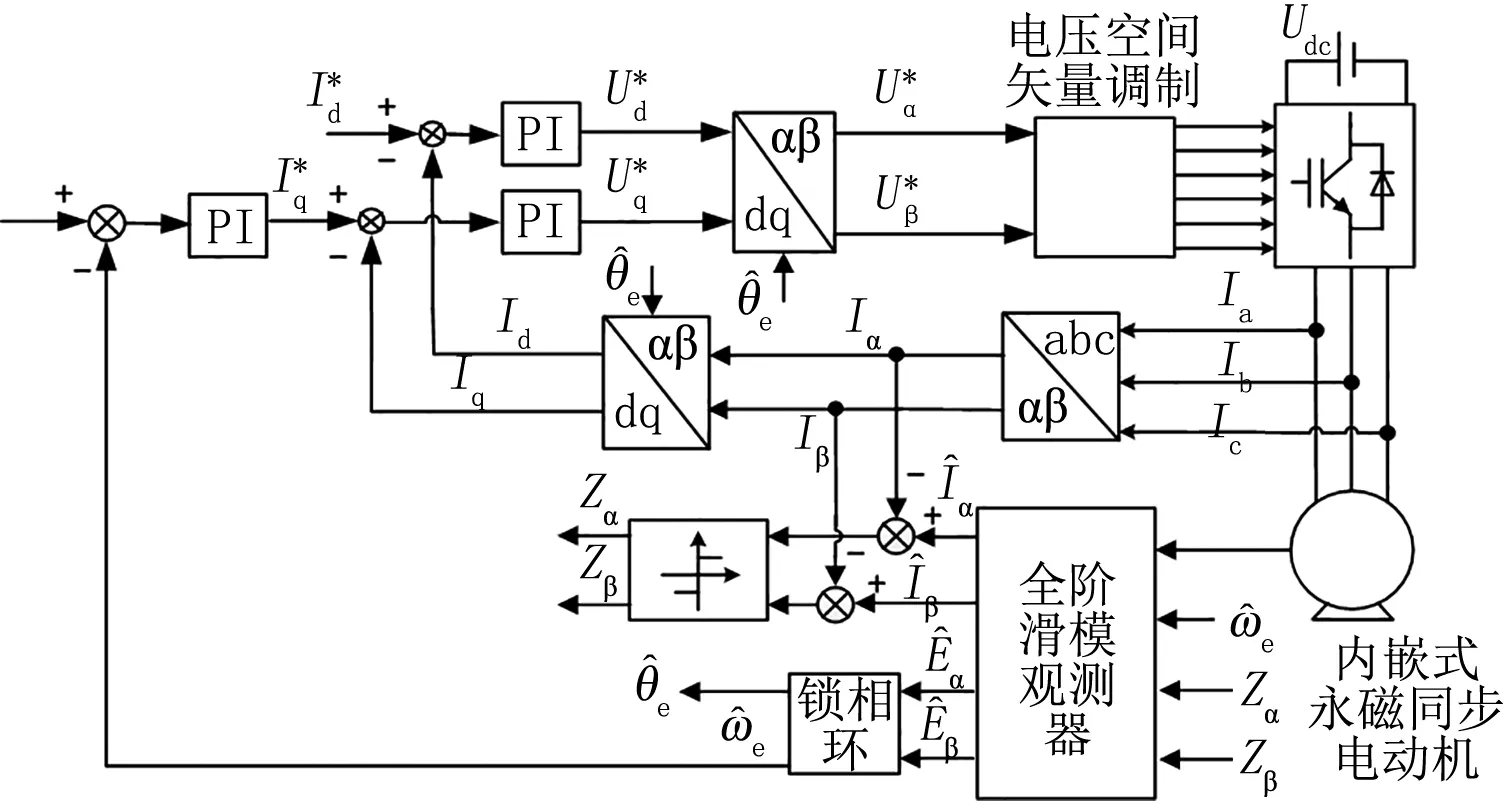
圖3 基于全階滑模觀測器的速度辨識系統框圖

在電動機控制系統中，轉速的變化率比起電流的變化率要慢很多，所以轉速的變化率近似為0，電動機反電動勢的變化率表達式如下：

(8)

將電流、反電動勢作為觀測變量，并以計算出的電動機電角速度代替真實電動機電角速度，得到下面的觀測方程：

(9)

式中I′為觀測的電流；E′為觀測的反電動勢。

其中

A′計算式中ω′e為觀測的電角速度。

由于反電動勢的測量比較困難，所以無法作為校正反饋項。定子電流的采樣測量是電動機控制器中的重要部分，其測量精度較高，很適合作為狀態觀測器的校正反饋項，根據自動控制理論中的全階狀態觀測器的誤差補償理論，在上面的觀測矩陣的基礎上，采用定子電流誤差構成的滑模面來作為校正項(誤差補償器)。

那么系統狀態方程就變成：

(10)

式中G為補償矩陣。

(11)

電流誤差構成的滑模面為

(12)

由于轉速的波動相對于電動機的電磁時間系數較低，可以近似為恒定值，得到觀測反電動勢與實際反電動勢的誤差方程表達式如下：

(13)

式中E*為靜止坐標系下的反電動勢誤差。

當系統進入滑模面時，觀測電流很接近真實電流，電流的觀測誤差為0，根據狀態觀測矩陣，反電動勢的誤差值可以表示為

(14)

得到反電動勢的誤差方程為

(15)

從上述表達式可以看出，反電動勢已經包含了卡爾曼濾波器中的預測和校正環節，所以不需要再對觀測的反電動勢進行額外的濾波，從而消除了對相位的補償。

2.2 自適應反饋矩陣系數設計

反饋矩陣的值決定了系統是否收斂，并且決定了收斂的速度，那么利用小信號分析理論的知識，可以對全階滑模狀態觀測器進一步分析，得到反饋矩陣選值的范圍及規律。

基于滑模面在靜止坐標系α軸系下的電流方程：

(Uα-E′α)+[-KZ(I′α-Iα)]}

(16)

觀測電流和實際采樣電流的跟蹤關系是分析電流方程中的重要環節。因此，可以將電流誤差值作為正定表達式：

V=(I′α-Iα)

(17)

忽略其中的電阻項，并假設靜止坐標系β軸系下的電流估算與實際電流一致：

(18)

已知，系統如要收斂，正定表達式的要求為

(19)

那么系數K需滿足：

K>|Eα-E′α|

(20)

再分析反電動勢的觀測方程：

(21)

將上式重寫成狀態函數如下所示：

(22)

(23)

化簡歸一后，得到如下方程：

(24)

從式(24)可以看出，其基本結構與標準的二階振蕩方程很接近，所以在工程上，可以采用二階振蕩的特性來近似，標準二階振蕩方程的表達形式如下：

(25)

式中ξ為阻尼比；ωn為自然振蕩角頻率。

(26)

(27)

(28)

經過以上理論分析，可以得到反饋矩陣系數的取值趨勢，傳統的取值方案是取較大的值覆蓋各種工況要求，保證系統的收斂性及穩定性。

圖4顯示了系統在滑模面上運動的軌跡，可知，當切換系數很大時，系統每次都會離滑模面較遠，下次再穿越滑模面去到另一邊，這會帶來較大的高頻抖振。

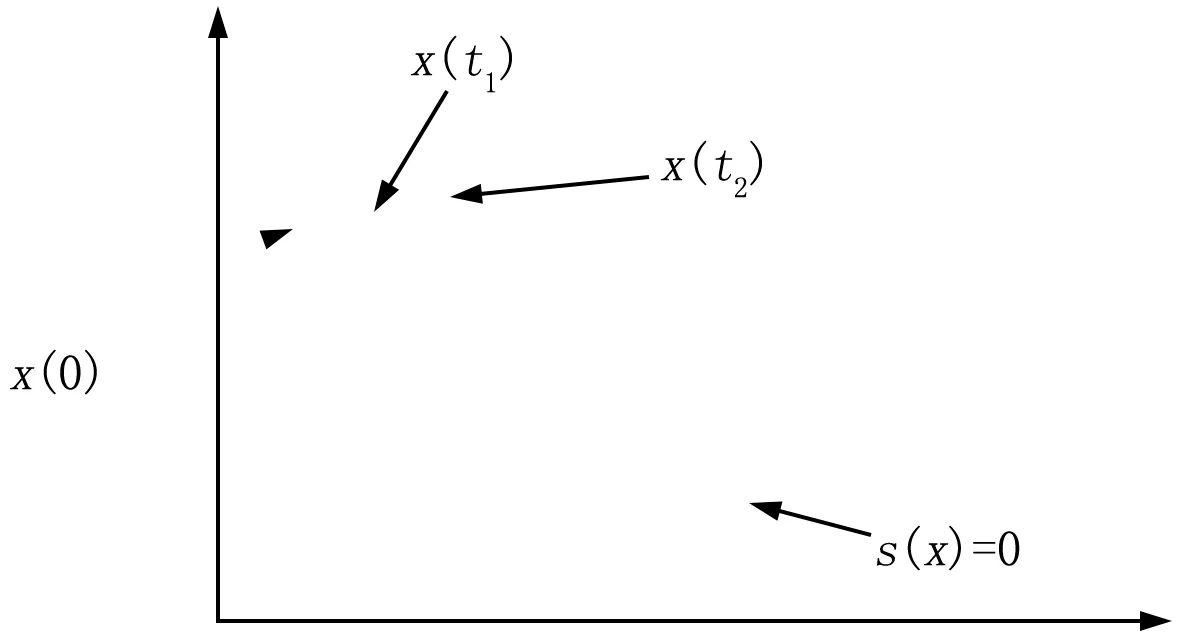
圖4 系統切換函數x(t)在滑模面上運行的軌跡

本文在保證系統收斂的前提下，通過上述分析，設計了一個反饋系數自由化。當系統剛啟動時，由于觀測的反電動勢還未跟蹤上真實的反電動勢，所以其誤差較大，需要較大的K值使系統穩定(K=K0)，在系統穩定后(時間t>t0)，觀測器觀測的反電動勢已經跟蹤上實際的反電動勢，此時可以降低K值(K=K1)。但是為了系統依舊收斂，同時考慮電流誤差的影響，當電流誤差較小時，系統收斂較好，觀測器跟蹤較好，所以此時可以使用較小K值(K=K2)來減小系統抖振；當電流誤差較大時，系統觀測效果差，可能會發生不收斂，所以采用較大K值(K=K3)來使系統穩定。最終的K值選取這2種取值中的大值，并且K值的變化都需要考慮切換的順滑性，切換示意如圖5、6所示。

圖5 K隨時間t的變化

圖6 K隨電流誤差Eer的變化

再利用觀測的轉速來實時更新系數K，使得系統工作在最佳欠阻尼狀態，提高了系統的魯棒性及穩定性。

3 實驗驗證

為驗證減小系統頻率抖振技術理論的正確性和利用優化滑模面切換函數、三階正交鎖相環設計等技術的有效性，通過MATLAB仿真和實物平臺聯合調試等技術手段驗證電動機反電動勢相位跟蹤誤差、頻率辨識精度、系統頻率抖振幅值大小的控制效果。采用GLDE-F80電動機設計了一套變頻空調控制系統，其主要參數見表1。

表1 變頻空調控制系統參數

傳統的二階滑模算法雖然可以辨識轉速及電動機轉子位置，但是其觀測的轉速波動較大(±10 r/min)，觀測反電動勢需要進行濾波，會帶來相位延遲(相位誤差為4°)。從上面的仿真結果可以看出，傳統滑模觀測器的觀測轉速波動較大，由于低通濾波器的原因，觀測的轉子位置存在較大相位誤差，并且誤差值隨轉速變化而變化，結果如圖7～9所示。

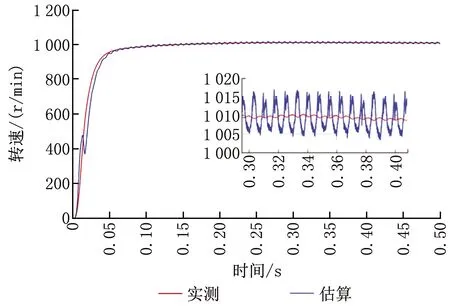
圖7 基于傳統的二階滑模算法的實測與估算轉速

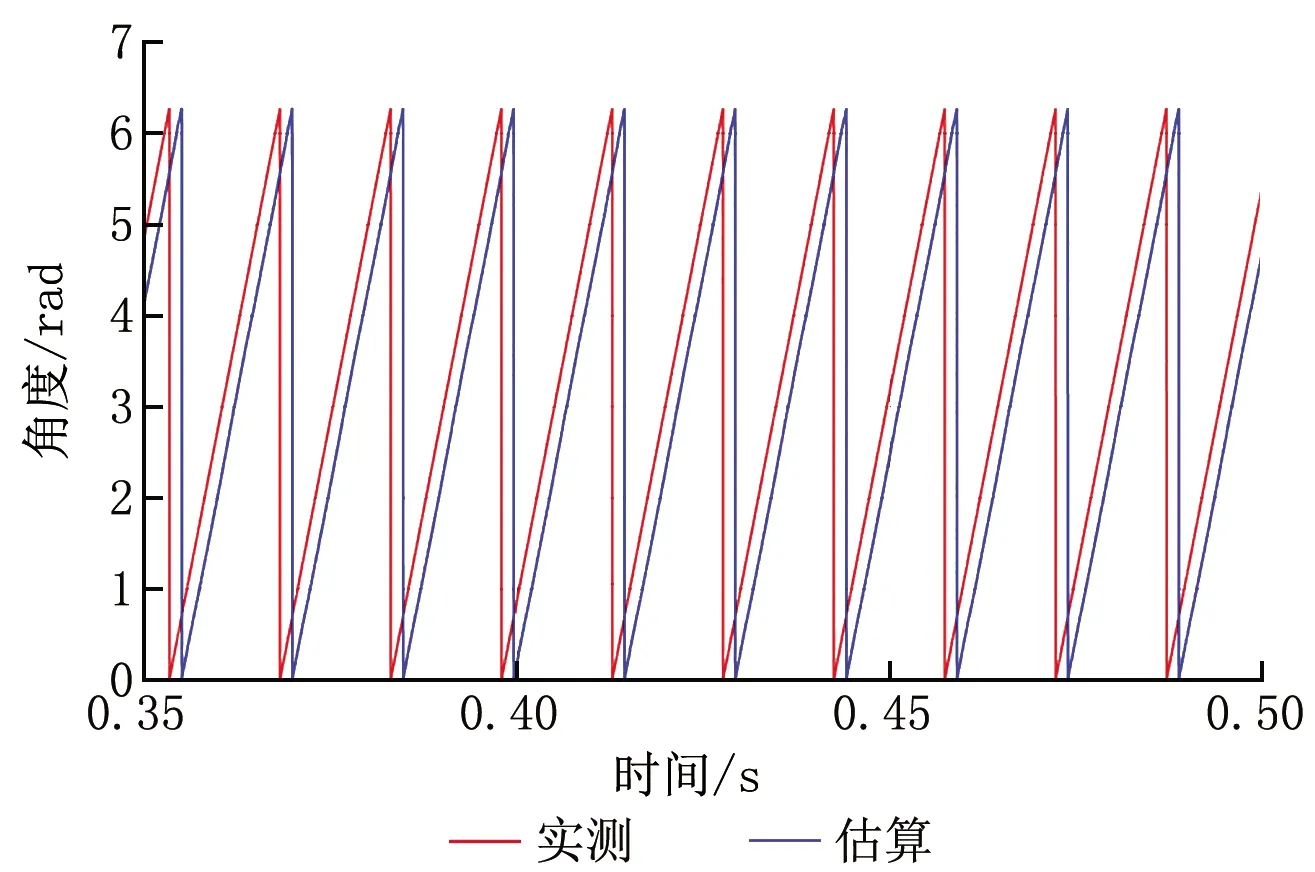
圖8 基于傳統的二階滑模算法的實測與估算角度

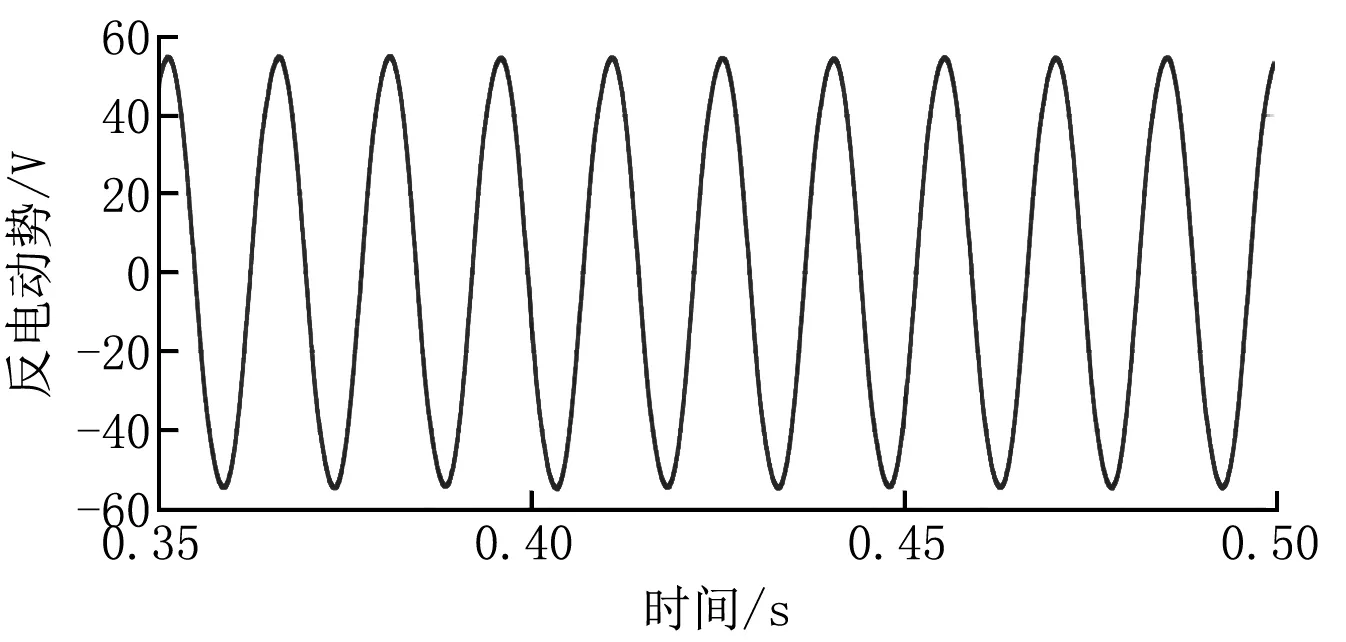
圖9 傳統的二階滑模算法的觀測反電動勢Eα

全階滑模觀測器的仿真結果如圖10～12所示，可以較好地提高觀測轉速性能。

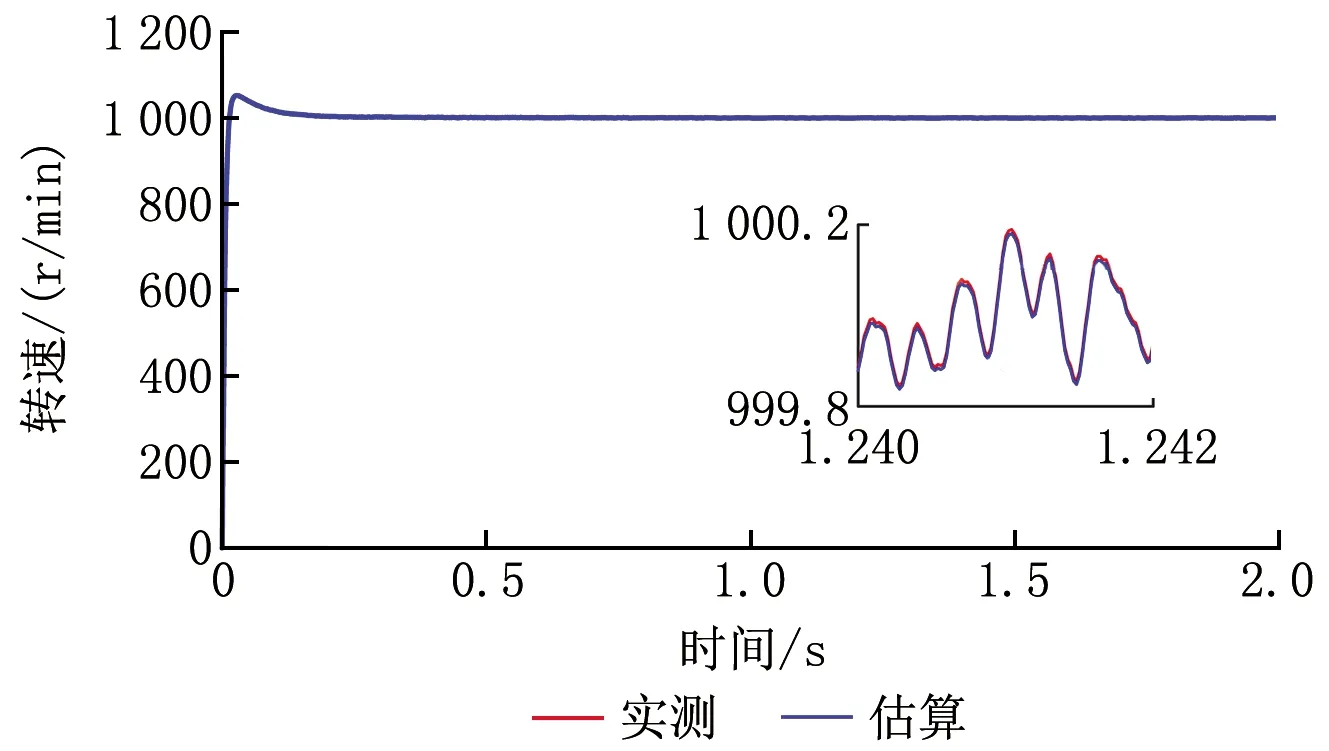
圖10 基于全階滑模觀測器算法的實測與估算轉速

由上述實驗波形可見，采用變增益滑模切換函數三階鎖相環通帶頻率的電動機反電動勢相位偏差減小至0，抖振頻率偏差精度控制在±0.2 Hz以內，實現了恒溫17.6 ℃、調濕5.4 g/kg的控制效果。

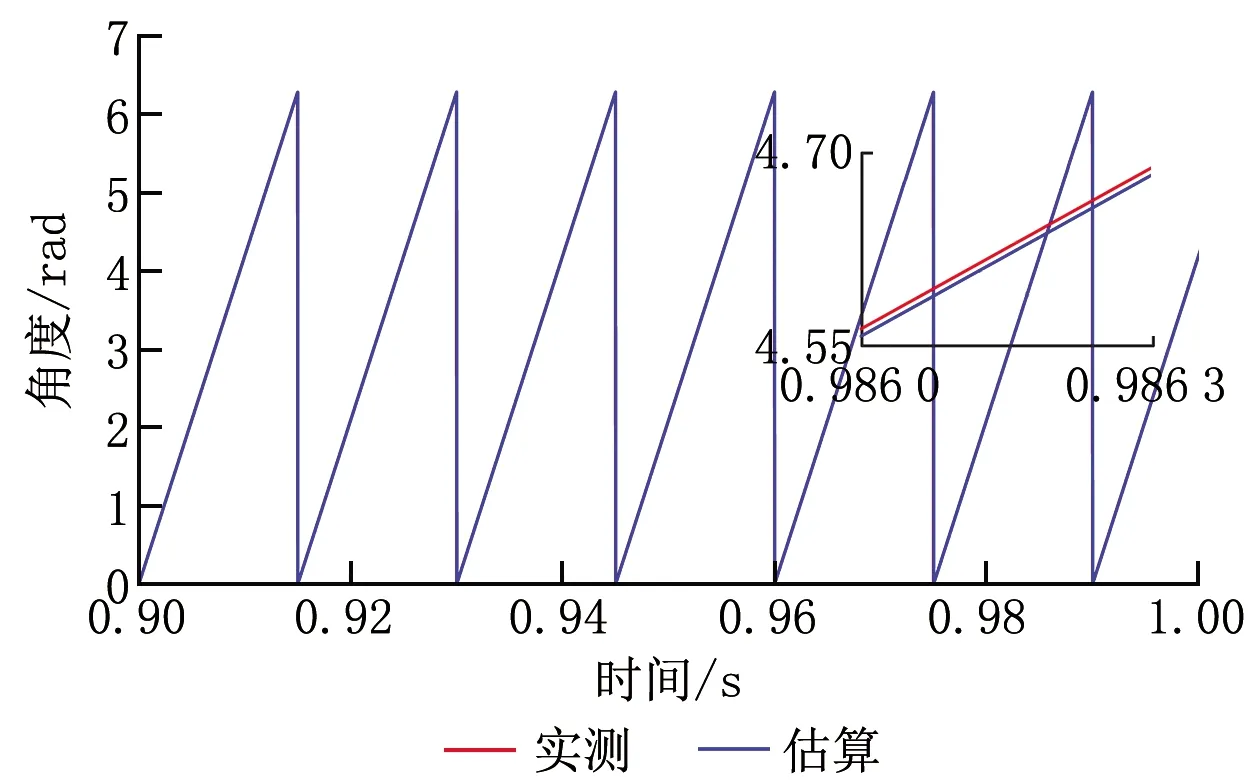
圖11 基于全階滑模觀測器算法的實測與估算角度

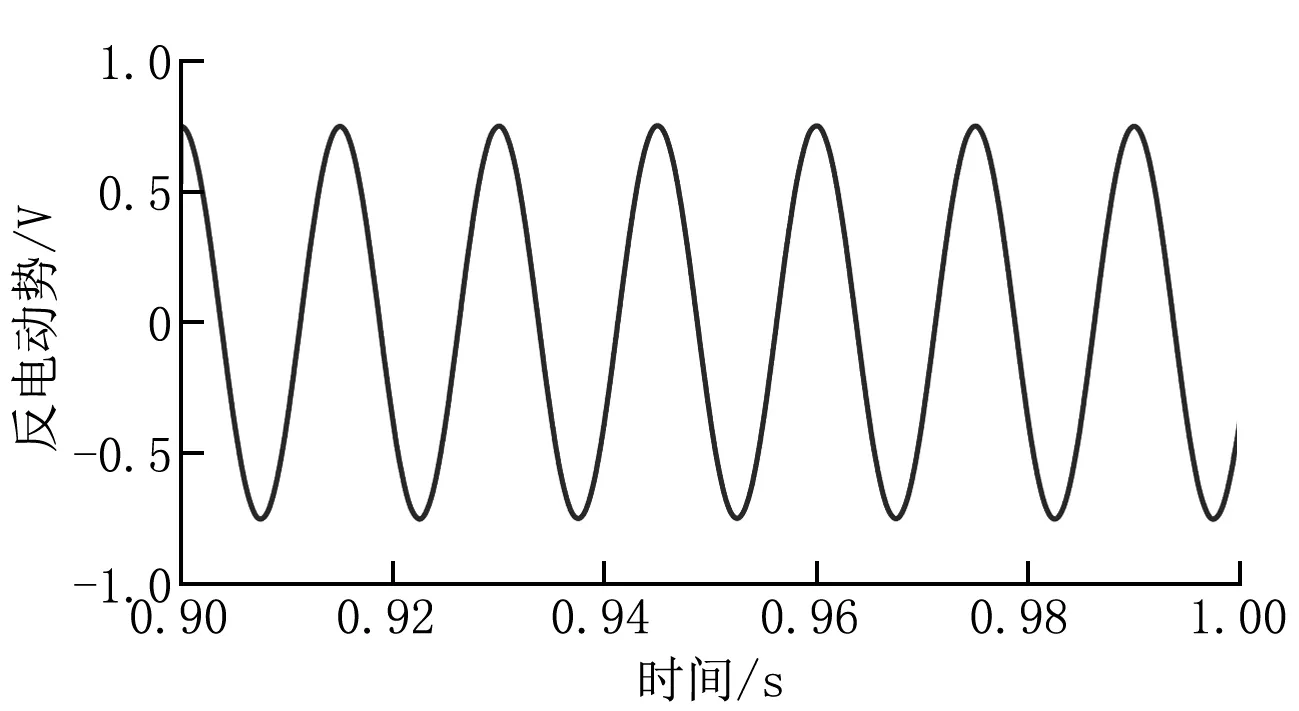
圖12 基于全階滑模觀測器算法的觀測反電動勢Eα

4 結語

針對改進全階滑模觀測器進行了研究，減小了變頻空調頻率抖振，實現了電動機反電動勢相位準確實時追蹤，并設計了變增益滑模切換函數，降低了系統頻率抖振幅值，利用三階鎖相環設計通帶頻率，降低了高頻部分的干擾，提高了電動機頻率辨識精度。保證了空調系統高效、恒溫及除濕性能，從而大幅提升變頻空調的能源利用效率。