借力轉化思維 增長學生智慧

文|鄭桂元

思維是借助語言、表象或動作，實現對客觀事物的概括和間接認識，是大腦一種復雜而高級的認知活動,它是人們思考認識問題的最重要方式。衡量人的思維能力高低的主要標志是人的思維的個性特征。數學作為一門基礎性、工具性學科，對學生思維能力培養具有十分積極的促進作用。在小學階段，需要培養的思維方式有很多，其中轉化思維是小學生需要掌握的最重要的思維方式之一。培養學生的轉化思維，有益于學生更好地學好數學、用好數學、增長智慧。其實我國古代就有許多運用轉化思維解決問題的經典故事，比如“圍魏救趙”“曹沖稱象”“司馬光砸缸”等，他們都是巧妙地運用轉化思維，創造性地解決了問題。可見，運用轉化思維往往是創新的一種體現。

一、運用轉化思維實現未知向已知轉化，化新為舊

小學數學教學中有許多新知識的教學都是引導學生通過將未知的新知識轉化為已知的舊知識，從而達到學習掌握新知識的目的。我們在教學這些知識時，不僅要引導學生能夠通過將未知轉化為已知，理解掌握新知。同時，我們還要借助學習新知的過程，引導學生反思感悟轉化的思維方式，并逐步養成遇到未知，能夠自覺運用轉化思維將未知轉化為新知解決問題的習慣，并逐步達到在日常生活中遇到未見過或未學過的新問題時，能夠有意識地運用轉化思維，尋找解決問題的途徑和方法，創造性地解決問題。

例如在教學《平行四邊形的面積》時，我們都是引導學生運用轉化思維將平行四邊形轉化為長方形，根據長方形的面積公式推導出平行四邊形的面積計算方法。在此基礎上，我們還應該引導學生思考，在遇到求平行四邊形的面積這個新問題時，我們是如何思考的，使學生感悟到運用轉化思維將它轉化成已經學過的長方形，尋找到解決問題的辦法。這個過程給你什么啟示？我們在以后如果遇到新問題時，可以怎么辦？從而使學生在掌握平行四邊形的面積的計算方法這個新知識的同時，領悟轉化思維這一重要的思維方式，為以后學生運用轉化思維解決問題奠定良好的基礎。后面學生在學習三角形的面積、梯形的面積、圓的面積等知識時就會自覺地嘗試運用轉化思維將新知轉化為舊知來解決問題。

二、運用轉化思維推動繁瑣向簡單轉化，化繁為簡

在小學數學教學中有時我們會遇到一些比較繁瑣的問題，解答起來比較困難。這時我們可以引導學生通過對問題的觀察分析，找到解決問題的突破口，運用轉化思維將繁瑣的問題轉化為簡單的問題，從而巧妙地解決問題。

例如在學習了《數的整除》這一部分內容后，我們可以讓學生嘗試解決這樣的問題：請為11338×25593=（ ）選擇合適的答案。

A.290133434 B.290173434

C.290163434 D.290153434

這道題看起來是一道計算題，如果我們通過計算出結果后，再選擇答案，那將是十分繁瑣的。應該如何來解決此題呢？我們可以啟發學生運用轉化思維，將這道計算題轉化為其他問題。可以引導學生這樣思考：在11338和25593這兩個數中，有沒有3的倍數？學生根據3的倍數的特征，發現11338這個數中1+1+3+3+8=16，16不是3的倍數，因此可以得出11338不是3的倍數。同時，因為25593這個數中2+5+5+9+3=24，24是3的倍數，因此可以得出25593是3的倍數。接著進一步引導學生思考一個3的倍數和一個不是3的倍數的數相乘，得到的積是不是3的倍數？為什么？從而得出它們的積一定是3的倍數。最后讓學生判斷四個給出的選項中哪個數是3的倍數？經過判斷可以快速得出只有選項B中290173434這個數各個數位上的數相加是3的倍數，因此只有290173434是3的倍數，符合要求，應該選擇選項B。這樣，我們就輕松地將一個十分繁瑣的計算題目，運用轉化思維將它轉化為簡單的判斷3的倍數的問題，真正實現了化繁為簡的目的。當然，我們在此基礎上還要引導學生進行深刻的反思，在以后解決一些看起來比較繁瑣的問題時，可以運用轉化思維，尋找到解決問題的捷徑，將它們轉化成其他比較簡單的問題，從而巧妙地解決問題。

三、運用轉化思維促使正向向逆向轉化，化正為逆

數學學習中有一些問題，如果從正方向去思考，有時解決起來比較困難，找不到解決問題的思路和方法，這時如果我們能夠打破思維定勢，嘗試使用轉化思維由正向思考向逆向思考轉化，很多時候能夠另辟蹊徑，出奇制勝，找到解決問題的方法，達到柳暗花明的效果。

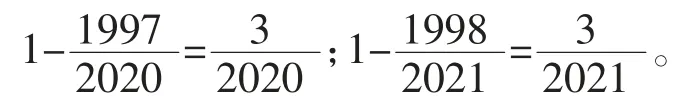
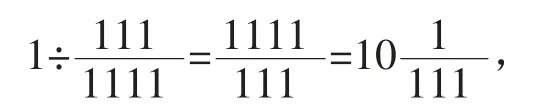
讓學生結合上面這兩個例子反思，通過解決這兩個問題給我們什么啟發？引導學生感悟當遇到一些運用正向思維很難解決的問題時，可以運用轉化思維，從問題的相反方向去考慮，往往能迎刃而解。其實“司馬光砸缸”故事運用的就是轉化思維，當因年齡和力氣比較小，無法實現讓人離開水時，司馬光機智地運用轉化思維，將正向轉化為逆向，讓水離開人，創造性地解決了問題。解答具體數學問題時可以運用轉化的思維化正為逆幫助我們解決問題。

四、運用轉化思維促成繁難向容易轉化，化難為易

小學數學教學中有些問題的解決需要綜合運用各種知識才能解決，并且解答過程非常復雜，給學生的解答帶來了很大的困難。當我們遇到這樣的問題時，可以運用轉化思維從宏觀思考，巧妙地將繁難的問題轉化為較容易的問題，從而實現問題的解決。

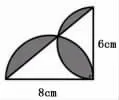
例如求上圖中陰影部分的面積。

這道題以直角三角形的兩條邊為直徑分別畫兩個半圓，計算陰影部分的面積。此題三個陰影部分均為不規則形狀，如果要通過直接計算的方式求陰影部分的面積將是十分困難的。我們可以引導學生通過有機整合，跳出常規思路，尋找出一條新的求陰影部分面積的方法。為了方便說明解題過程，我們可以先給圖中的每個獨立的部分分別命名為①～⑤。根據圖中各部分面積之間的關系，我們可以得出：

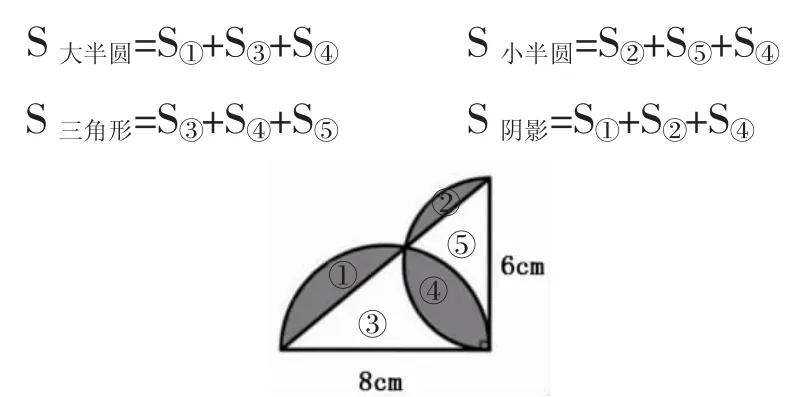
經過對比我們可以發現：

根據以上分析，解答過程如下：

S大半圓=3.14×（8÷2）2÷2=25.12（cm2）

S小半圓=3.14×（6÷2）2÷2=14.13（cm2）

S三角形=6×8÷2=24（cm2）

S陰影=25.12+14.13－24=15.25（cm2）

借助圖形各部分之間的關系，我們就把一個繁難的問題巧妙地解決了。在此基礎上引導學生思考，通過解決這個問題我們有什么感悟？學生通過深入思考可以發現，這其實就是運用轉化思維，將求陰影部分面積轉化為尋找大半圓、小半圓、三角形和陰影部分的面積之間的關系，從而化難為易，解決了問題。這時可以進一步引導學生反思，通過這種解決問題的方式，給你哪些啟示？使學生感受到當我們在解決問題的過程中遇到困難時，不要囿于常規的解決問題方法，而是要嘗試運用轉化思維換一個角度尋求解決問題的途徑，找到更簡捷的解決問題的方法。

四、運用轉化思維達到由數向形轉化，見微知著

著名數學家華羅庚曾說過：“數缺形時少直觀，形少數時難入微；數形結合百般好，隔離分家萬事休。”可見數與形之間存在密切的聯系，在解決問題時我們可以根據需要將二者之間相互轉化。在教學中當我們遇到一些認識和理解比較困難的問題時，我們可以運用轉化思維在數與形之間進行轉化，從而達到“以數解形”或“以形顯數”的目的。

例如在教學《近似數》一課時，學生對如何確定一個大數的近似數掌握起來比較困難，這時我們可以借助“形”這個工具來幫助學生理解。首先，我們可以提出以下問題讓學生嘗試解答：

1.猜一猜：12875寫成近似數，接近多少萬？

2.說一說：學生說明自己的想法。你是怎樣想的？

3.看一看：送你一個工具，出示數軸。請在數軸上找到12875的位置在哪里？請觀察12875是離10000近，還是離20000近？

4.想一想：12875寫成近似數，接近多少萬？

（12875≈1000012875≈1萬）

接著引導學生思考：你還能找出哪些整數寫成近似數是1萬？這些數有什么共同特點？分別在數軸的什么地方？學生通過思考后得出5001～14999之間的整數寫成近似數后都是1萬。想一想，有沒有例外的數？你能找出來嗎？學生很快就能找出是10000，因為它等于1萬。

然后再讓學生思考：哪些整數寫成近似數是2萬？最大的數是多少？最小的數是多少？在此基礎上引導學生總結概括求近似數的方法“四舍五入”就水到渠成了。這樣，借助轉化思維將數轉化成形，學生對四舍五入的理解就不再是抽象的概念，而是學生頭腦中形象直觀的區間了，使學生對近似數的相關知識的理解也變得直觀形象了。

轉化思維是一種重要的思維方式，它能起到化新為舊、化繁為簡、化正為逆、化難為易、見微知著的作用。運用轉化思維往往能夠達到“山窮水盡疑無路，柳暗花明又一村”的效果。轉化思維的培養，不僅能幫助學生解決學習中遇到的難題，還可以幫助學生解決生活中遇到的實際問題。更重要的是使學生增長了智慧，使學生思考問題時有了新的途徑和方法。在很多時候，轉化思維表現出的就是創新的思想。因此，在小學數學課堂教學中我們要結合不同的教學內容，有意識地培養和發展學生的轉化思維，從而不斷提升和發展學生的數學素養，增長學生的智慧。