病態乘性誤差模型的加權最小二乘正則化迭代解法及精度評定

王樂洋，陳 濤，鄒傳義,2

1. 東華理工大學測繪工程學院，江西 南昌 330013； 2. 武漢大學測繪學院，湖北 武漢 430079

在大地測量數據處理領域中，若觀測誤差隨觀測量的大小或物理信號的強弱而變化，則該類誤差為乘性誤差[1]。例如，現代觀測手段中的合成孔徑雷達SAR觀測值的隨機誤差表現為乘性誤差[2-3]，光電測距EDM(electronic distance measurement)和全球定位系統GPS的觀測誤差表現為乘性誤差或者加乘性混合誤差[4-5]。目前，在大地測量領域中關于乘性誤差模型參數估計和精度評定的研究成果相對較少[6-9]，且其中尚無文獻針對乘性誤差模型中存在的病態問題進行研究，因此如何對病態乘性誤差模型進行參數估計和精度評定是值得研究的問題。

病態問題廣泛存在于測繪數據處理中，模型的病態性會造成參數解的不穩定，甚至嚴重偏離真值[10]。已有的總體最小二乘病態問題[11]、大地測量反演的病態問題[12]和控制網平差的病態問題[13]等都是基于加性誤差模型建立的，而對于乘性誤差模型的病態問題尚未發現研究成果。乘性誤差模型的最小二乘解法最早由文獻[6]提出，文獻[7]在文獻[6]的基礎上，總結了乘性誤差模型的最小二乘、加權最小二乘和偏差改正加權最小二乘方法，并推導了參數估計的精度評定公式。若直接采用文獻[7]中的3種方法處理病態乘性誤差模型，而不考慮系數矩陣的病態性，會使參數估值產生偏差且不穩定。文獻[4]為避免系數矩陣病態，將模擬點集中在數字地面模型(digital terrain model,DTM)中的峰值處，其他的點均勻分布，這僅可用來處理模擬數據，無法適用于真實的觀測數據。系數矩陣病態會使得系數矩陣的列向量之間存在復共線性，進而引起法方程條件數過大，導致解不穩定[10]。目前，處理病態問題的方法主要有Tikhonov正則化法[14-16]和虛擬觀測值解法[17]等。正則化參數的確定方法，主要有廣義交叉核實法[18]、嶺跡法[19]和L曲線法[20-22]等。廣義交叉核實法難以獲得最優解，適用性弱；嶺跡法雖然計算簡單，但有一定的主觀性；L曲線法適用性強，并且能獲得較為合理的正則化參數，被廣泛用于正則化參數的選取，可以很好地用于本文算法中正則化參數的選取。

經分析發現，使用加權最小二乘正則化法求解病態乘性誤差模型時，參數估值是觀測值的非線性函數，而觀測值的協因數陣是參數估值的非線性函數，并且在逐步迭代的過程中參數的每一步估值都具有隨機性，使得最終的參數估值與觀測值為復雜的非線性關系，只能使用數值方法迭代求解，無法得到解析解。因此本文引入無需求導、無需獲取非線性函數具體表達式的SUT法[23-24]對病態乘性誤差模型進行精度評定。

綜上所述，針對已有文獻未考慮乘性誤差模型的病態性，本文首先利用Tikhonov正則化方法導出病態乘性誤差模型的加權最小二乘正則化解，其次通過SUT法對病態乘性誤差模型進行精度評定；最后通過兩個模擬數據算例和一個真實數據算例驗證本文方法的適用性及優勢。

1 乘性誤差模型

給定一組帶有乘性誤差的觀測值，相應的乘性誤差模型可以表示為[7]

(1)

隨機模型為

(2)

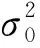
進一步可將式(1)改寫為如下形式

y=f(β)⊙(1+εm)

(3)

式中，⊙表示哈達瑪乘積符號。

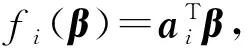
y=(Aβ)⊙(1+εm)

(4)

式中，A=[a1,a2,…,an]T；β=[β1,β2,…,βt]T。

由式(4)可知，在乘性誤差模型中，觀測值精度與系數矩陣和參數估值的乘積有關：信號Aβ越強，觀測值y的誤差越大；反之，信號Aβ越弱，誤差越小。這明顯區別于傳統的加性誤差模型，即觀測值y的誤差與系數矩陣和參數估值無關。目前，已有關于乘性誤差模型的研究均不考慮系數矩陣A病態[7-8]，然而在大地測量實際數據處理中，系數矩陣A很容易出現病態，此時會引起法方程條件數過大，觀測量微小的擾動將會引起參數較大的變化，導致解不穩定。例如，文獻[25]針對SAR型噪聲的特性采用乘性誤差模型進行影像去噪，去噪效果達到70%～93%。此時，若系數矩陣A病態，會引起法方程條件數過大，導致解不穩定，進而影響影像去噪。因此需要針對病態乘性誤差模型進行更深入的研究來豐富現代大地測量數據處理理論。

2 病態乘性誤差模型參數估計的加權最小二乘正則化迭代解法及精度評定

2.1 病態乘性誤差模型參數估計的加權最小二乘正則化解法

為了更方便地進行公式推導，將式(4)改寫為如下形式

y-Aβ=(Aβ)⊙εm

(5)

令

(6)

(7)

根據最小二乘準則求解式(6)，得

(8)

β的最小二乘估值為

(9)

根據前文中的分析可知，當法方程N=ATA病態時，由式(9)求得的最小二乘解不可靠。因此，引入正則化因子α，構建如下病態乘性誤差模型的正則化準則

(10)

對式(10)中的β求偏導，并令其為0，可得

(11)

將式(6)代入式(11)，可得病態乘性誤差模型的加權最小二乘正則化解

(12)

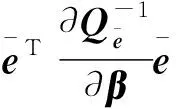
進而可以得到

(13)

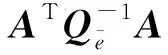
2.2 L曲線法基本原理

在確定本文病態乘性誤差模型中的正則化參數時，由于觀測值的協因數陣為參數估值的非線性函數，因此觀測值的權陣也為參數估值的非線性函數，這使得正則化參數值產生動態變化。

2.3 病態乘性誤差模型的精度評定

根據文獻[8]，病態乘性誤差模型的單位權方差估值可表示為

(14)

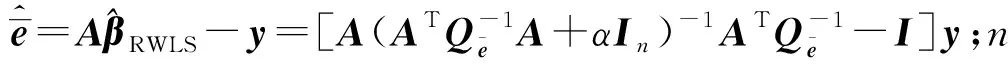
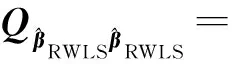
(15)

由偏差的定義[26]，對式(13)兩邊取期望，可得參數估值的偏差為

(16)

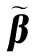
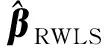
(17)

病態問題中，由于產生了偏差項，此時的均方誤差不等于協方差不能作為一個良好的精度評判標準。雖然最小二乘估值是無偏，但已不是最優值[7]。根據均方誤差的定義[30-31]，可知均方誤差的表達式為

(18)

式中，等式右邊第1部分表示參數估值協方差的跡；第2部分表示參數估值偏差平方的跡。

2.4 病態乘性誤差模型參數估計的加權最小二乘正則化迭代解法

式(13)的迭代公式如下所示

(19)

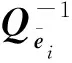
綜上所述，本文將病態乘性誤差模型的加權最小二乘正則化法迭代解法命名為算法1，具體步驟如下：

(1) 采用最小二乘法求得參數估值的初始值

(20)

(3) 求得正則化參數αi。

(4) 根據式(19)迭代求得病態乘性誤差模型加權最小二乘正則化迭代解。

3 病態乘性誤差模型精度評定的SUT法

由算法1可以看出，病態乘性誤差模型的加權最小二乘正則化迭代解法中，每一步迭代參數估值都是觀測值的函數，而觀測值的協因數陣又是參數估值的函數，使得最終的參數估值與觀測值為一個復雜的非線性函數。本文將這種非線性關系表示為[32-33]

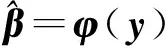
(21)

式中，φ(·)表示參數估值與觀測值y之間的非線性函數。

第1步參數迭代估值可以表示為[32-33]

(22)

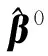
最終的參數估值表達式為[32-33]

(23)

式(23)表明，病態乘性誤差模型的加權最小二乘正則化法的迭代過程使得參數估值和觀測值之間的非線性關系非常復雜，且迭代的過程使參數的每一步的估值都具有隨機性。為了避免復雜的公式運算，本文在病態乘性誤差模型加權最小二乘正則化法中引入SUT采樣法，旨在獲得更精確的參數估值和精度信息。

本文將病態乘性誤差模型精度評定的SUT法命名為算法2，步驟如下：

(1) 確定采樣的先驗統計均值和協方差陣。本文將觀測值和對應的協方差陣作為采樣的先驗統計均值E(y)和協方差陣D(y)。

(2) 基于先驗統計均值和協方差陣構造采樣點集{χi}(i=0,1,2,…,2n)，生成2n+1個采樣點

(24)

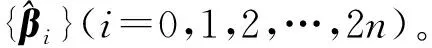
(4) 確定采樣點集的權

(25)

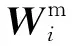
(5) 計算參數估值的均值和均方誤差陣

(26)

(27)

(6) 計算單位權方差

(28)

本文首先對病態乘性誤差模型加權最小二乘正則化迭代解法進行改化，將病態乘性誤差模型中參數估值與觀測值表示為嵌套函數的形式，然后引入無需求導、無需了解非線性函數構造的SUT法求解病態乘性誤差模型中參數估值的均值、均方誤差矩陣和單位權方差。

4 算例及分析

為了比較不同方法下參數估值和精度信息的差異，分別使用文獻[7]中的未考慮病態性的三種方法即最小二乘法、加權最小二乘法和偏差改正加權最小二乘法，以及本文提出算法1和算法2進行解算。5種方案及對應的方法見表1。

表1 5種方案及對應的方法

4.1 算例1

為了驗證本文公式推導以及算法的有效性，算例1根據文獻[34]改編得到，通過利用GPS測量某一區域道路中心線地面點的高程，假定該區域道路中心線地面點高程真值與某一坐標原點的距離除以100符合以下函數模型

y=10+2x+x2+x3+0.5x4

(29)

式中，y為地面點高程的真值；x為高程點與某一坐標原點的距離除以100。

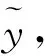
假設地面點高程真值被乘性誤差干擾，其中乘性誤差向量εm相互獨立，且服從均值為0、標準差為0.1的正態分布，即εm～(0,0.12×I31)，相應的乘性誤差模型的觀測方程為

Y(x)=y(x)⊙(1+εm)

(30)

式中，Y(x)為受乘性誤差干擾的地面高程點觀測值向量；1為元素全為1的31維列向量；εm為31維乘性誤差向量。

由式(30)得到一組地面高程點的數據模擬值見表2。為了說明高程點受乘性誤差的影響程度，本文將地面高程點受乘性誤差干擾前后的數據繪于圖1中。

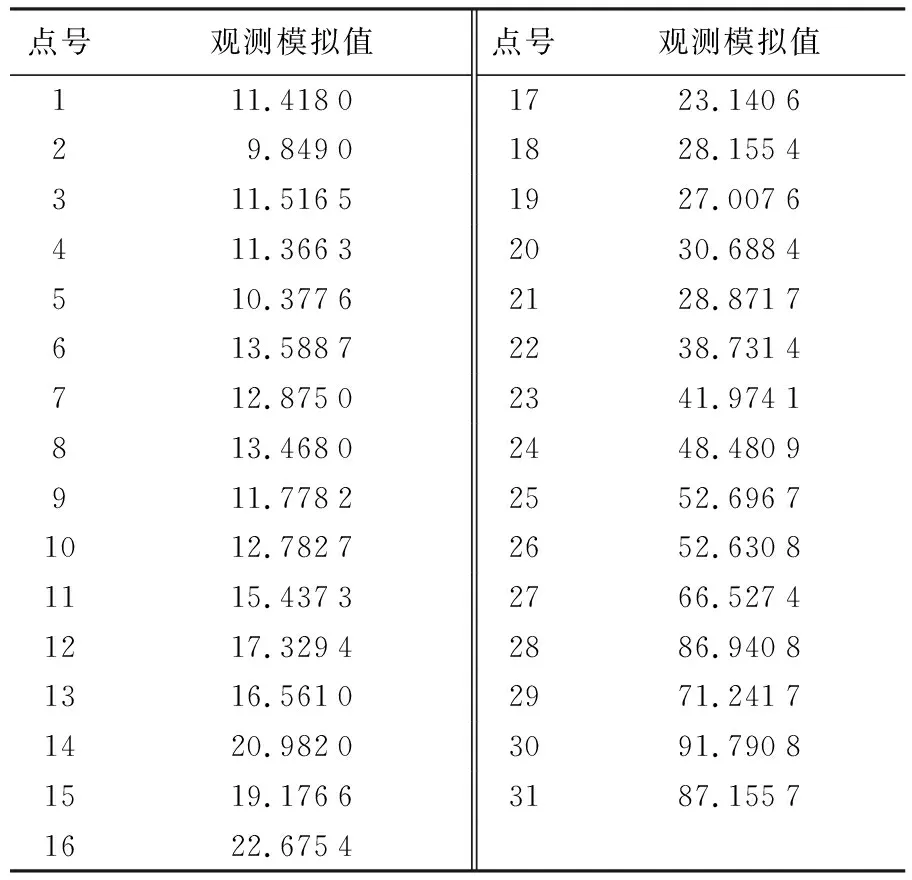
表2 數據模擬值

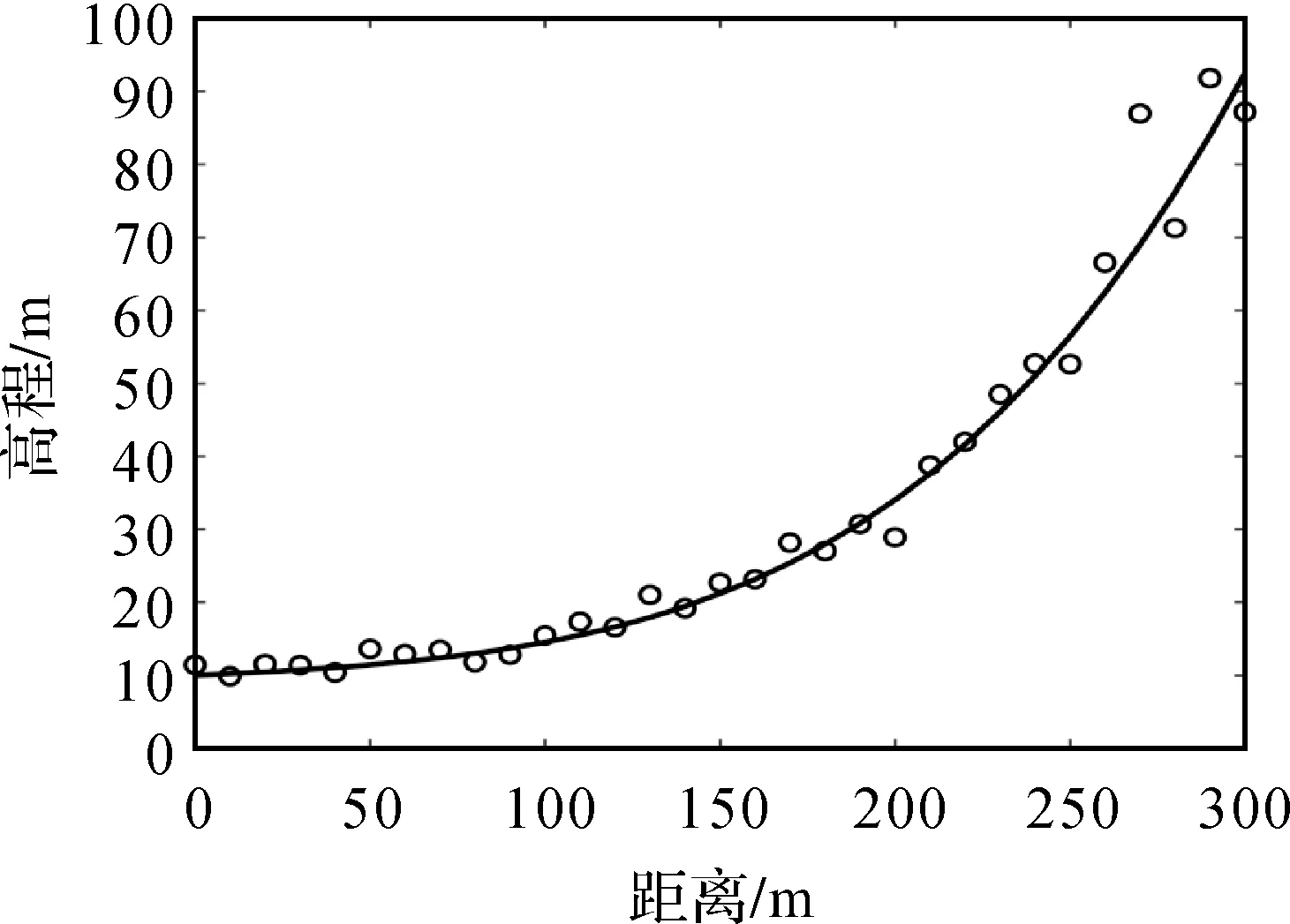
圖1 地面高程點受乘性誤差干擾前后分布Fig.1 GPS elevation points before and after disturbed by multiplicative error

本算例選取的單位權中誤差σ0為0.3。使用表1中的5種方案計算，將參數真值、5種方案計算的參數估值、參數估值與真值的2范數及單位權中誤差估值列于表3；5種方案計算的參數估值的均方根誤差列于表4。

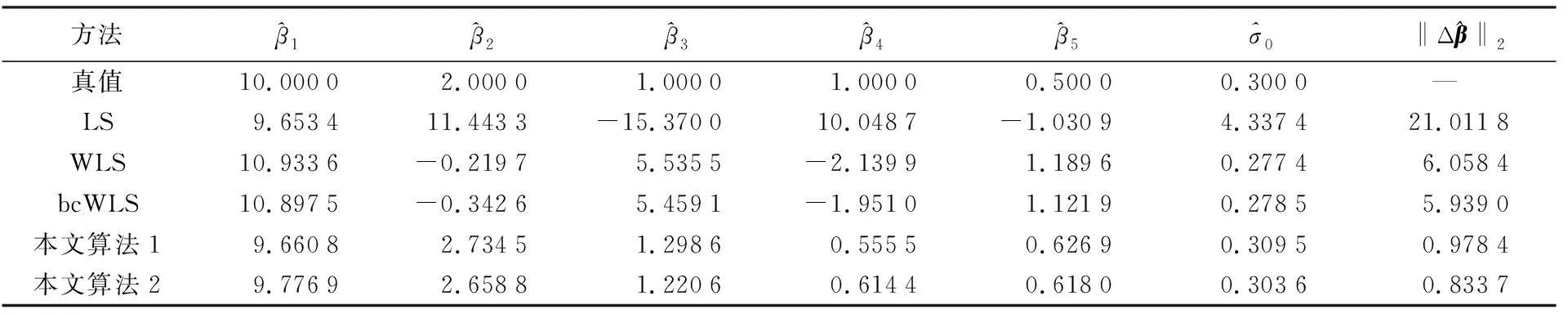
表3 參數估值、參數估值與真值之間的2范數和單位權中誤差

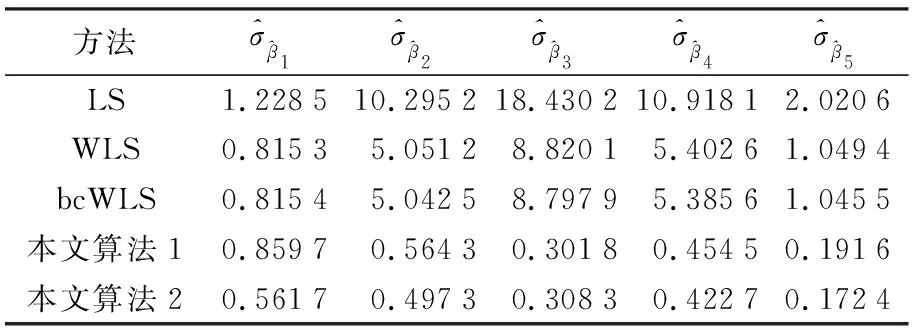
表4 參數估值的均方根誤差

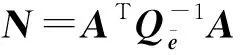
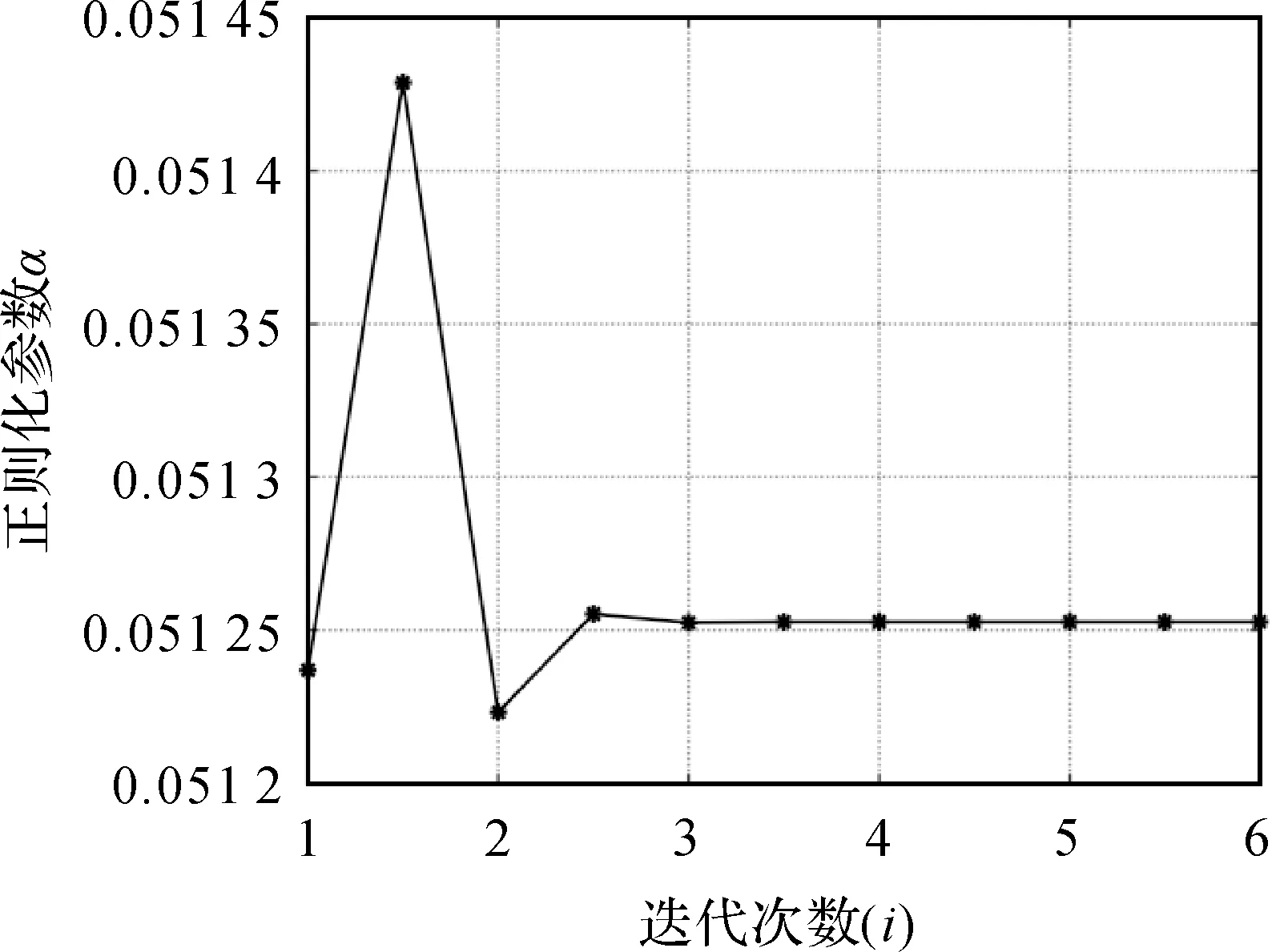
圖2 正則化參數α隨迭代次數的變化Fig.2 The regularization parameter with the number of iterations

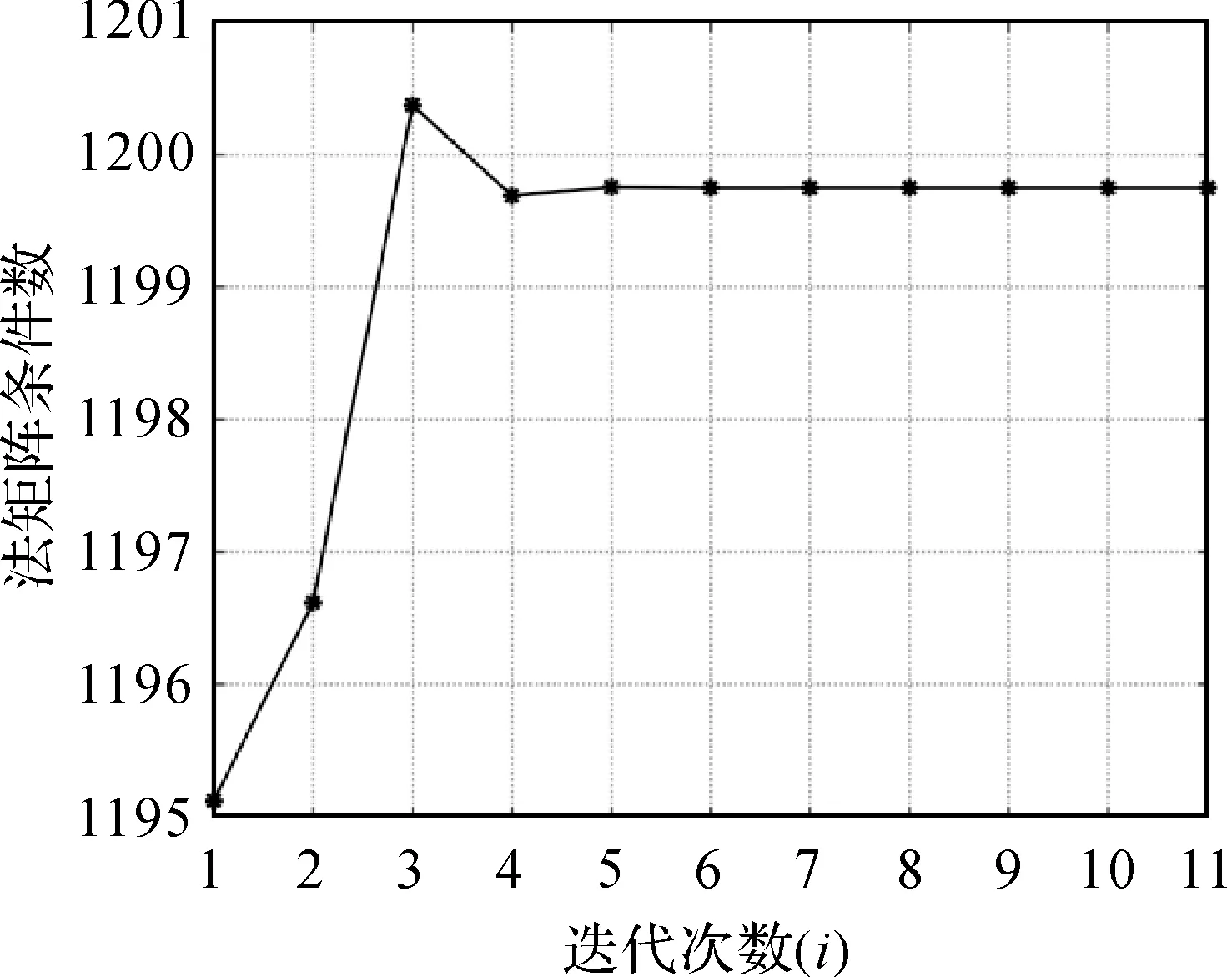
圖3 法矩陣條件數隨迭代次數的變化Fig.3 The condition number of the normal matrix with the number of iterations

由圖1可知，由于地面高程點受到乘性誤差干擾，導致點位產生了嚴重偏離。由表3中參數估值與真值的2范數可知，LS方法求得的2范數結果最大；WLS方法由于考慮了觀測值的權得到的結果優于LS法，其2范數為6.058 4；bcWLS方法對WLS方法進行了偏差改正，2范數較WLS方法減小了0.119 4，為5.939 0，但由于未考慮模型的病態性，仍與真值偏離較大。本文算法1和算法2求得的2范數分別為0.978 4和0.833 7，參數估值更接近真值，說明本文算法對于降低病態性有一定的效果。其中，由于算法2考慮了正則化解法逐步迭代過程中每一步的隨機性和非線性迭代的過程對參數估值的影響，求得的2范數較算法1減小了0.144 7，表明了本文使用SUT法的可行性。由表3中的單位權中誤差可知，由于文獻[7]中的方法未考慮模型的病態性，導致求得的單位權中誤差偏離真值，而本文算法考慮了這些影響，求得的單位權中誤差更接近真值，進一步表明了本文算法的優勢。

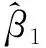
4.2 算例2

算例2為一個DTM模型的算例，本文主要考慮模型為病態的情況，因此模擬一個病態DTM模型。文獻[4]在模擬DTM模型時，為防止法矩陣病態情況出現，在模擬的DTM模型的每個峰值周圍采樣更多點，并使峰值點之間遠離，雖然可以在一定程度上降低病態性，但僅可用來處理模擬數據，無法適用于真實的觀測數據。本文依據文獻[4]的思路，使用插值法來模擬DTM模型，插值法是模擬DTM模型的主要方法之一[35-36]，本文模擬的DTM模型由下面的插值函數生成

(31)

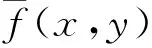
函數fi(x,y)(i=1,2,3,4)分別為如下

f1(x,y)=exp{-((x-22)2+(y-22)2)/500}

(32)

f2(x,y)=exp{-((x-28)2+(y-28)2)/500}

(33)

f3(x,y)=exp{-((x-25)2+(y-25)2)/500}

(34)

f4(x,y)=exp{-((x-20)2+(y-20)2)/500}

(35)

模擬的DTM模型如圖4所示，相應的乘性誤差模型的觀測方程為

(36)

式中，h(x,y)為受乘性誤差干擾的觀測值向量；1為元素全為1的1681維列向量；εm為1681維乘性誤差向量。

在本文中，假設誤差向量εm相互獨立、且服從均值為0，標準差為0.1的正態分布，即εm～(0,0.12×I1681)。為了說明DTM模型受乘性誤差的影響程度，本文將不含誤差的觀測值繪于圖4中，受乘性誤差干擾的觀測值繪于圖5中。

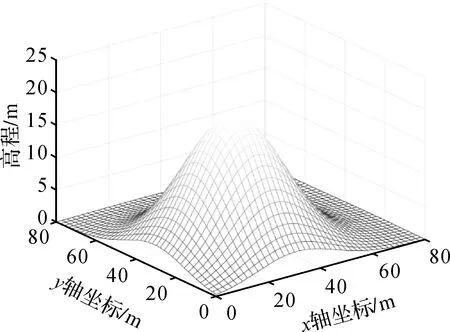
圖4 模擬的DTM模型Fig.4 Simulated DTM model

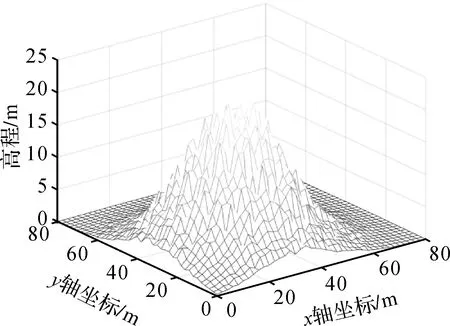
圖5 受乘性誤差干擾的DTM模型Fig.5 DTM model disturbed by multiplicative error

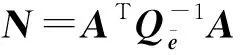
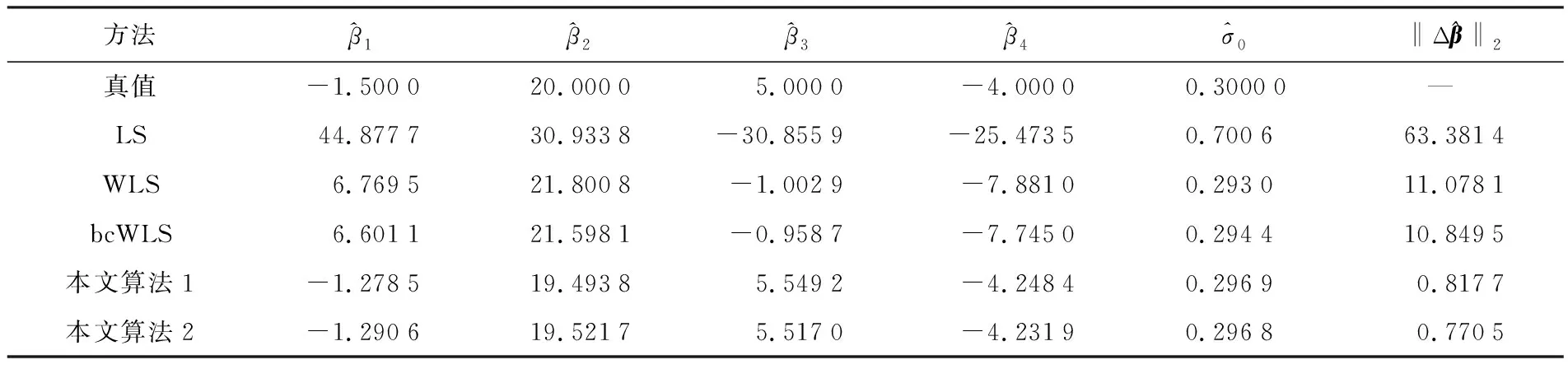
表5 參數估值、參數估值與真值之間的2范數和單位權中誤差

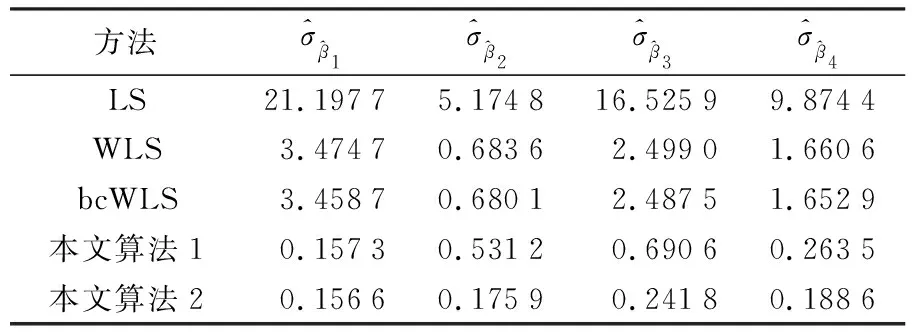
表6 參數估值的均方根誤差

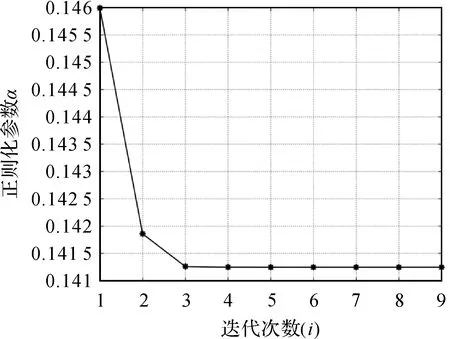
圖6 正則化參數α隨迭代次數的變化Fig.6 The regularization parameter with the number of iterations

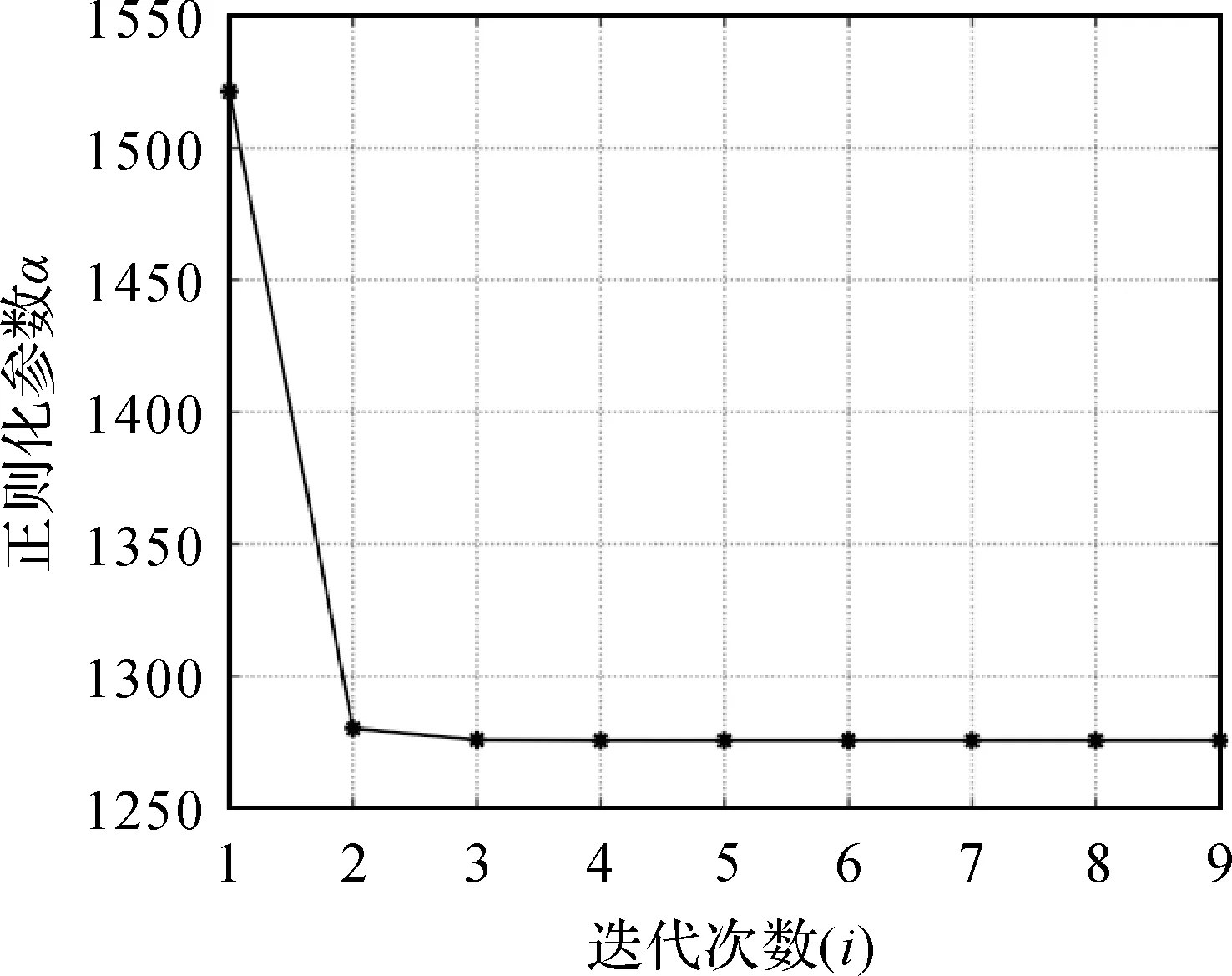
圖7 法矩陣條件數隨迭代次數的變化Fig.7 The condition number of the normal matrix with the number of iterations

由圖4和圖5可以發現，盡管本文模擬的DTM模型加入的乘性誤差標準差僅為0.1，但對高程產生了較大的影響，此時法矩陣的條件數為5.190 5×104，嚴重病態。因此，針對病態乘性誤差模型數據處理理論需要進行更深入的研究。

由表5可得，由于未考慮模型的病態性，文獻[7]中的方法求得的參數估值嚴重偏離真值，而本文算法求得的結果更接近真值，參數估值的2范數分別為0.817 7和0.770 5，比bcWLS方法小了10.031 8和10.079 0，進一步說明本文算法對于降低病態性有一定的效果。其中，本文算法2考慮到非線性迭代的過程對參數估值的影響，求得的2范數最小，這與算例1得到的結果一致。由表5中的單位權中誤差可知，LS方法求得的單位權中誤差0.700 6，結果嚴重偏離真值；WLS方法和bcWLS方法由于考慮了觀測值的權，求得的單位權中誤差比LS方法更接近真值，為0.293 0和0.294 4；本文算法考慮了病態性對單位權中誤差的影響，求得的單位權中誤差最接近真值。

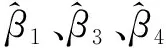
4.3 算例3

為進一步說明本文方法的可行性和適用性，算例3為一個病態數字高程模型真實數據算例。數字高程模型是一種承載地面高程信息的空間數據模型，是DTM模型的一個分支，本文主要利用SRTM(shuttle radar topography mission)提供的免費DEM數據集，通過在網站http:∥srtm.csi.cgiar.org/srtmdata/下載了2304個點的三維坐標數據來說明本文算法在實際應用中的優勢。SRTM數據是由航天飛機雷達測量生成的LiDAR影像數據[37]，且LiDAR數據的噪聲已被證明具有乘性噪聲性質[38]，因此本文含有6個未知參數的數字高程DEM乘性誤差模型如下

H(xi,yi)=F(xi,yi)⊙(1+εm)

(37)

式中，(xi,yi)表示地面點經緯度坐標；H(xi,yi)表示該點對應的高程，單位為米；εm表示乘性誤差向量。

F(xi,yi)的具體形式如下[7]

(38)

由于SRTM數據均是在等精度測量中獲取，因此在定權時假設未知的單位權中誤差和乘性誤差相等，即乘性誤差的權陣為單位陣。本文獲取的受乘性誤差干擾的數字高程模型如圖8所示，分別使用表1中的5種方案計算，WLS方法和bcWLS方法由于受病態性的影響，系數矩陣奇異，參數估值不收斂；LS方法、本文算法1和2方法擬合的數字高程模型如圖9、圖10和圖11所示。將3種收斂方案計算的參數估值和單位權中誤差估值列于表7，參數估值的均方根誤差列于表8。

表7 參數估值和單位權中誤差

表8 參數估值的均方根誤差

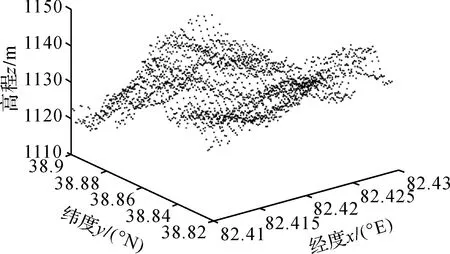
圖8 受乘性誤差干擾的數字高程模型Fig.8 Digital elevation model disturbed by multiplicative error

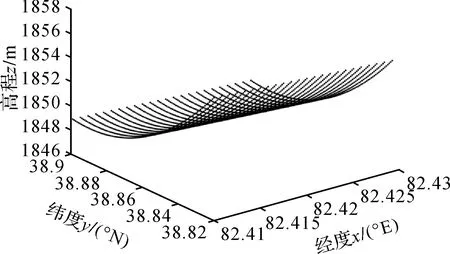
圖9 LS方法求得的數字高程模型Fig.9 Digital elevation model obtained by the LS method

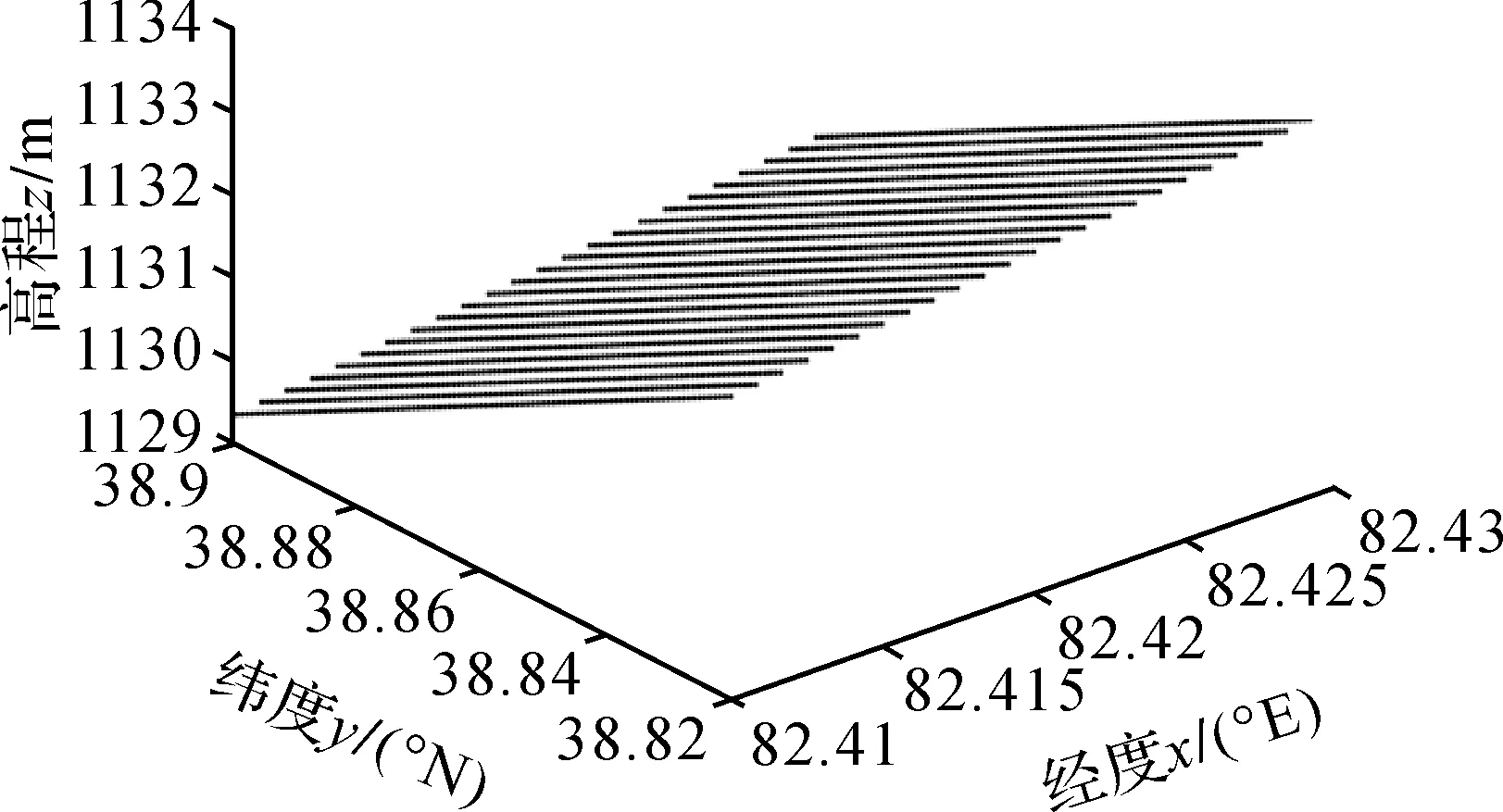
圖10 RWLS方法求得的數字高程模型Fig.10 Digital elevation model obtained by the RWLS method

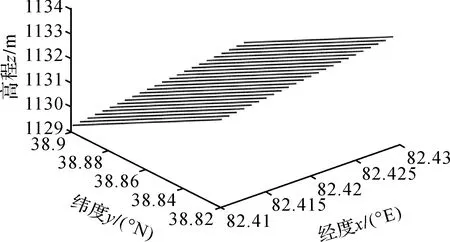
圖11 SUTRWLS方法求得的數字高程模型Fig.11 Digital elevation model obtained by the SUTRWLS method

由圖8和圖9可以發現，LS方法求得擬合高程的結果嚴重偏離原始的數字高程模型，這是由于LS方法未考慮觀測值的權且模型為病態性所導致的。本文算法考慮了病態性的影響，在處理實際數據時更具優勢，從圖10和圖11來看，求得擬合高程的結果能夠較好地擬合圖8的高程。說明現有文獻未考慮病態性的方法無法處理實際數據，因此顧及模型病態性帶來的影響是十分必要的。

由表7可以看出，LS方法求得的參數估值和單位權中誤差過大，不符合實際情況，進一步說明了LS方法無法處理實際數據，本文算法在處理實際數據的優勢。由表8也可以看出，LS方法求得參數估值的根均方誤差最大，本文算法遠小于LS方法。其中，在本文算法中，由于算法2考慮了非線性迭代過程對參數估計帶來的影響，使用SUT法求得的參數估值的均方根誤差小于算法1，這也驗證了本文算法的適用性和優勢。對比算法1和算法2在參數估值上并沒有很大差別，這可能是因為參數估值較小；而參數估值的均方根誤差卻差別很大，這是因為算法1根據誤差傳播定律求得的均方根誤差只能反映參數估值的一階精度信息，而算法2采用的SUT法為二階精度評定方法，求得參數估值的精度信息為二階精度。

5 結 論

為了完善乘性誤差模型數據處理理論，本文在分析已有研究的基礎上，將乘性誤差模型擴展至病態乘性誤差模型，推導了病態乘性誤差模型參數估計的Tikhonov正則化迭代解公式。考慮到迭代過程中參數估值與觀測值之間存在復雜的非線性關系，引入SUT法對病態乘性誤差模型進行精度評定。最后，通過算例的驗證與分析得到以下幾點結論：

(1) 本文推導的病態乘性誤差模型參數估計的Tikhonov正則化迭代解法可以得到比未考慮模型病態性的方法更準確的參數估值，且參數估值的精度更高。

(2) 通過將加權最小二乘正則化迭代過程表示成非線性函數，引入的SUT精度評定方法能夠得到更為合理的精度信息。

(3) 本文提出的方法是基于函數f(·)為β的線性函數的情況下推導的，若將函數f(·)擴展至非線性函數，需要進一步研究。