齒輪軸上圓錐滾子軸承的預緊
仇靜,常方坡,劉海林,袁正,劉志新
(安徽合力股份有限公司,安徽 合肥 230601)
引言
隨著對噪音水平的要求越來越高,斜齒輪的使用日益廣泛,尤其在電動車類的產品中。在使用平行軸斜齒輪的齒輪箱中,齒輪軸和傳動軸既承受軸向力又承受徑向力,因此承受軸向力較大的軸的支撐常選用圓錐滾子軸承。在圓錐滾子軸承的使用中,發現預緊力過大,齒輪箱容易在使用初期出現異響、軸承損壞。因此,使用圓錐滾子軸承時,需要給予合適的預緊力,不當的預緊甚至成為早期齒輪箱損壞的直接原因。
1 圓錐軸承預緊概述
圖1 為圓錐滾子軸承的壽命與軸向游隙的關系圖[1],當對軸承進行適當預緊時,軸承的壽命最長;若預緊力過大,則軸承壽命急劇下降;若預緊力過小,軸承的軸向游隙較大時,同樣壽命較短。所以如何確定軸向預緊力,成為使用圓錐滾子軸承需要解決的重要問題。在裝配過程中,如何有效控制并便捷地完成預緊,也成為許多企業和科研機構關注的問題。

圖1 圓錐軸承的壽命和軸向游隙的關系
2 齒輪受力分析
如圖2 所示,雙聯齒輪軸上背對背安裝著兩個圓錐滾子軸承,對雙聯齒輪軸進行定位,在圓錐滾子軸承2 的內圈外裝有鎖緊螺母,預緊雙聯齒輪軸上的圓錐滾子軸承。齒輪軸通過兩個斜齒輪傳遞功率,圓錐滾子軸承1 和圓錐滾子軸承2 和同時承受軸向力和徑向力。
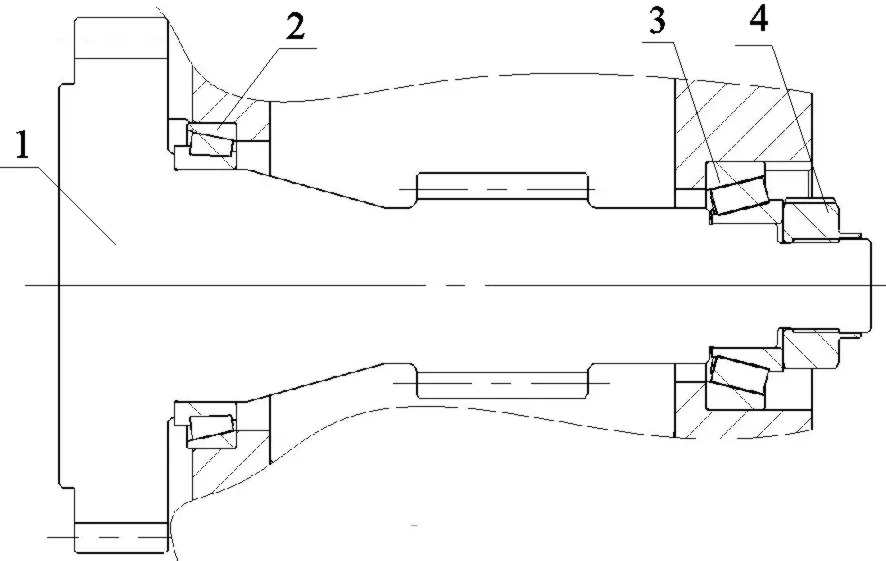
圖2 齒輪軸結構圖
為了確定圓錐滾子軸承1 和圓錐滾子軸承2 的軸向預緊力,需對雙聯齒輪軸上的每對齒輪進行受力分析,計算出每個圓錐滾子軸承所受的軸向力和徑向力,最后根據軸向力確定圓錐滾子軸承軸向預緊力的大小。
單對齒輪的受力分析[2]:
圓周力:

徑向力:

軸向力:

式中:T0——傳動軸上的扭矩(N.m);d——齒輪的節圓直徑(m);Ptan——單對齒輪嚙合產生的切向力(N);Pnor——單對齒輪嚙合產生的徑向力(N);Pth——單對齒輪嚙合產生的軸向力(N);αt——齒輪的端面壓力角(°);β——螺旋角(°)。
3 軸承受力分析及預緊力計算
3.1 軸承受力分析
如圖3 建立直角坐標系,[1]為軸承1 作用點的位置,[2]為軸承2 作用點的位置。軸承1 作用點和軸承2 作用點之間的作用力為齒輪產生的,多對齒輪產生的作用力按照一定的關系式進行累積,具體計算公式如下:
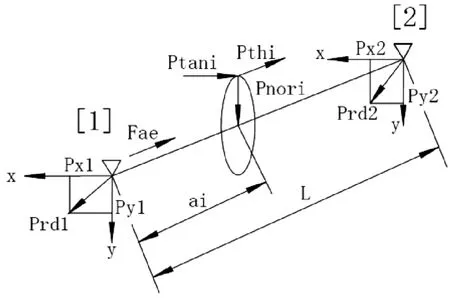
圖3 軸承作用點受力分析
作用在軸承1 作用點處的徑向載荷Prad1(N):
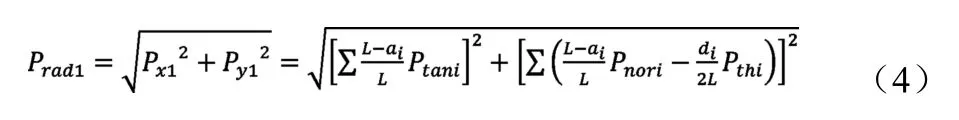
作用在軸承2 處作用點的徑向載荷Prad2(N):
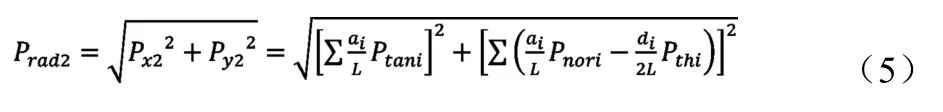
式中:Px——x 方向載荷(N);Py——y 方向載荷(N);ai——i 齒輪作用點距離軸承1 作用點的距離(m);L——軸承1 作用點和軸承2 作用點之間的距離(m)。
軸承的外部軸向力計算:

圓錐滾子軸承一旦承受徑向載荷,便會產生軸向的分力[2]。圓錐滾子軸承1 和圓錐滾子軸承2 分別承受徑向載荷Prad1和Prad2。假設軸向外部載荷Fae方向如圖3 中所示,則圓錐滾子軸承1 和圓錐滾子軸承2 承受的軸向載荷分別為Fa1(N)和Fa2(N):
式中:Y1——軸承1 的軸向負荷系數;Y2——軸承2 的軸向負荷系數。
3.2 預緊力計算
該齒輪軸應用于電動叉車齒輪箱,叉車的典型工況分別為滿載全速、空載全速和滿載爬坡。表1 所示分別為空載全速、滿載全速和滿載爬坡三種工況下,圓錐滾子軸承1 和圓錐滾子軸承2 所承受的軸向力和徑向力。根據表1 數據可以看出:空載全速工況時,圓錐滾子軸承1 的徑向最大載荷為2345N,軸向最大載荷為1396N,圓錐滾子軸承2 的徑向最大載荷為1446N,軸向最大載荷為903N;滿載全速工況時,圓錐滾子軸承1 的徑向最大載荷為3761N,軸向最大載荷為2241N,圓錐滾子軸承2 的徑向最大載荷為2319N,軸向最大載荷為1450N,各項載荷均約為空載全速工況下各項載荷的160%;滿載爬坡工況時,圓錐滾子軸承1 的徑向最大載荷為30737N,軸向最大載荷為18293N,圓錐滾子軸承2 的徑向最大載荷為18956N,軸向最大載荷為11833N,各項載荷均約為空載全速工況下各項載荷的1310%,為滿載全速工況下各項載荷的817%,滿載爬坡工況下的各項載荷值,遠遠大于空載全速和滿載全速的載荷。
滿載爬坡的特點為載荷大、速度慢,工作時長占比小;空載全速和滿載全速的特點為速度較高,載荷相對較小,工作時長占比大,空載全速和滿載全速的載荷差值相對于滿載爬坡時也小很多。若按照滿載爬坡工況來計算圓錐滾子軸承的軸向預緊力,可能會使軸承90%以上的時間,處于重預緊狀態。一般情況下,叉車在使用過程中,空載全速和滿載全速工作占整個叉車工作的大部分時間,滿載全速的載荷包含了空載全速的載荷且載荷值相差相對較小,滿載全速工況的工作時長占比較大,所以滿載全速工況為圓錐滾子軸承預緊的主要考慮工況。
根據軸承廠家經驗,由于電動車的工作環境較好,一般取的軸向預緊力需大于滿載全速工況下最大軸向載荷的一半,最大軸向力的一半(即大于1121N)。
由于圓錐滾子軸承預緊力F(N)和軸向變位δa(m)近似成正比關系(如下式所示[3])。在此處,考慮該齒輪軸實際應用的叉車工作時,地面會有一定的坡度,為了保證大部分工況下圓錐滾子軸承的支撐剛度,在滿足設計要求的圓錐滾子軸承壽命的情況下,盡量選取最常用工況下的最大軸向力作為預緊力。此處,通過壽命計算(計算公式如下[2])圓錐滾子軸承的軸向預緊力設為最大軸向力時,其壽命仍滿足要求,因此,該處鎖緊螺母對圓錐滾子軸承施加的軸向預緊力設為2400N 左右。
預緊力和軸向變位關系:

軸承壽命為:

式中:L10——額定疲勞壽命(106旋轉單位);P——當量動載荷(N);C——基本額定動載荷(N);X——徑向負荷系數;Y——軸向負荷系數。
4 裝配時預緊力的控制
圓錐軸承預緊力調整方法主要有:
(1)手感控制法:邊擰緊螺母邊轉動齒輪,通過手感確定軸承的預緊力,該控制法需要大量的經驗,實際操作時無法定量控制,存在不穩定性。
(2)鎖緊螺母力矩控制法:通過控制鎖緊螺母的擰緊力矩來控制預緊力的大小,該方法控制簡便,便于操作,但由于摩擦力矩受到摩擦系數波動的影響較大,為了控制裝配時的一致性,對鎖緊螺母、螺紋制造精度水平等有一定的要求。
其中,鎖緊螺母的擰緊力矩T與預緊力F的關系[2]:
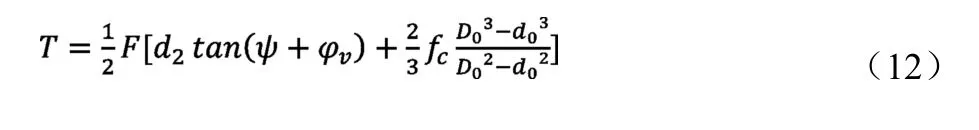
式中:D0——螺母環形支撐面的外徑;d0——螺栓孔直徑;d2——螺紋中徑;fc——螺母與支撐面之間的摩擦系數;φv——螺旋副的當量摩擦角;ψ——螺紋升角。
(3)啟動力矩控制法:通過測量裝配后的軸承總成在擰緊前后的啟動力矩的差值來控制軸承的預緊,可有效地控制力矩大小,操作簡便性遜色于方法二,但對相關零件的制造精度要求較低,對制造成本的控制較為有利。
其中,圓錐滾子軸承的預緊力F和起動摩擦力矩M的關系:

式中:e——圓錐滾子端面和擋邊的接觸位置;β——1/2滾子的圓錐;μe——滾子端面與擋邊的摩擦系數0.2。
5 總結
本文針對齒輪軸上圓錐滾子軸承的預緊問題,進行了齒輪和軸承的受力分析。根據圓錐滾子軸承的壽命與軸向游隙的關系,并針對叉車的常用工況,計算了圓錐滾子軸承的預緊力。為了方便實際裝配,研究了軸承預緊力與啟動力矩,及啟動力矩與鎖緊螺母摩擦力矩的關系,分析了各自的特點,可為裝配提供簡便的操作方式。

