考慮區間彈性連接的結構動力學特性研究*

陳亦文，張錦光

（1.武漢大學后勤保障部，武漢 430070；2.武漢理工大學機電工程學院，武漢 430070）

0 引言

當前，工程實際中的結構系統如火箭、導彈、衛星、高鐵、船舶等日趨復雜，復雜結構系統通常由不同形狀的板、梁等結構構成主體結構，由大量機械連接（如螺栓、鉚釘等）進行裝配。然而這些機械連接并非“純”剛性連接，而是剛度較大的彈性連接，為了提高結構系統的可靠性和環境適應性，連接剛度的影響不容忽視［1-2］。文獻［3-4］對具有彈性連接結構的動力學特性進行了研究，文獻采用6 自由度標量彈簧對連接剛度進行等效，然而這種方法忽視了連接剛度6 自由度間的耦合作用，等效精度不足。文獻［5-6］指出，空間梁單元的剛度矩陣存在6自由度間的剛度耦合，可更為準確地描述機械連接剛度。此外，工程中的機械連接通常有許多參數（如幾何尺寸、材料參數等）具有不確定性，這些不確定因素有可能導致結構的固有頻率漂移，因此，在研究彈性連接的動力學特性時，應充分考慮不確定因素帶來的影響［7-8］。

近年來，區間分析方法在處理區間結構動力學問題方面的應用日益增多，而在處理此類問題的過程中，區間分析方法的核心問題是有限元控制方程的求解［9］。目前用于求解區間方程組的常用方法為區間攝動法［10］以及組合求解法［11］，然而，這兩種方法均較難實現考察結構某一區間不確定參數對結構動力學特性影響的目的，IFM 的提出則可有效地解決這一問題。文獻［12-15］基于IFM 對區間結構的振動特性以及動力響應開展了研究工作，并總結出了IFM 的基本思想和使用步驟，即：1）將結構的區間參數寫成其區間中心值與區間因子乘積的形式；2）將區間結構的質量矩陣、阻尼矩陣和剛度矩陣分別寫成確定性質量矩陣、阻尼矩陣和剛度矩陣與結構區間參數區間因子乘積的形式；3）將區間結構的固有頻率、振型，以及動力響應等寫為包含各區間參數區間因子顯式的函數，并基于區間分析方法計算所關注對象的區間上下限和區間中心值。

此外，對于日益復雜的工程結構，其離散后的自由度往往是數以十萬、百萬計，因此，直接利用傳統的有限元方法計算其動力學特性，對計算機的工作性能帶來了嚴峻挑戰。動態子結構方法是處理分析復雜結構動力學特性的高效方法，常用的動態子結構方法包括時域的CMS 和頻域的FBSM。CMS 方法是一種高效計算理論模型耦合動力學問題的時域方法，目前已在商業軟件中得到應用［16-17］，但由于該方法對于處理試驗模型的耦合問題存在限制，因此，FBSM 得到了越來越多的關注。FBSM 的發展經歷了從最初的阻抗耦合方法到導納耦合方法，再到后來可用于直接處理多個子結構間耦合問題的廣義導納耦合方法［18-20］，直到形成現有可用于處理考慮彈性連接的多個子結構間耦合問題的FBSM［21-23］，其計算精度和計算效率不斷提高，適用范圍也越來越寬，在工程實際中得到了廣泛應用。

基于上述闡述，筆者利用具有區間彈性模量和比例阻尼系數的零質量空間梁單元，模擬復雜結構中的區間彈性連接，綜合動態子結構方法和區間因子法，提出了計算考慮區間彈性連接結構動力學特性的高效時域和頻域方法，即CMS-IFM 和FBSM-IFM，并通過數值仿真對兩種方法進行了驗證。相比傳統的有限元方法計算動力學特性，該方法不再受計算機工作性能的限制，可大幅提高計算效率，為大規模的推廣應用奠定了基礎，可廣泛應用于飛行器、航天器、船舶以及車輛等的連接結構中。

1 考慮彈性連接的結構固有頻率

設整體結構是由P 和Q 兩個子結構組成，且兩個子結構間為n 個參數相同但相互獨立的彈性連接（即pi～qi，i=1，2，…，n），則具有彈性連接的整體結構示意圖如圖1 所示。

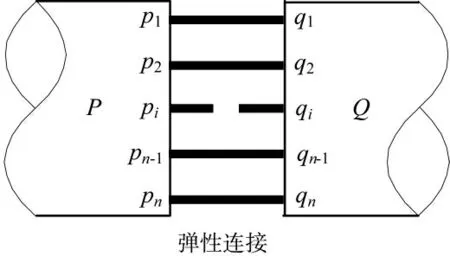
圖1 整體結構示意圖

通常情況下，根據CMS 中子結構的劃分原則，可將圖1 所示的整體結構劃分成P 和Q 兩個子結構，二者的界面結點集分別為Pv和Qv，考慮到彈性連接剛度的影響，兩個子結構界面節點自由度位移并不連續，無法直接利用CMS 對整體結構的動力學特性進行準確分析。為了解決這個問題，本研究將圖1 所示整體結構劃分成P、Q 和C 3 個子結構，其中C 為連接子結構，且令連接子結構C 只有界面結點，如下頁圖2 所示。連接子結構C 的劃分，則可使界面位移協調條件得到滿足。

待子結構劃分完成后，根據CMS 的工作原理，首先按照內部結點自由度u 和界面結點自由度v 將主子結構P 和Q 的質量和剛度矩陣進行分塊整理，即MP、KP和MQ、KQ，并在此基礎上分別計算兩個主子結構的假設模態集φP和φQ（由保留主模態和約束模態組成）［24］。

圖2 子結構劃分示意圖

國內外學者在研究機械連接對整體結構動力學特性的影響時，通常忽略連接質量的影響，即令連接質量為零［22-23］。同時，上述提到可利用空間梁單元的剛度矩陣來等效彈性連接的剛度，因此，本研究利用零質量空間梁單元來對彈性連接進行等效。

空間梁單元的剛度矩陣Kb寫為如下形式：

式中，Kb1為確定矩陣，其表達式參見文獻［1］，E 為彈性模量。

又由于連接子結構C 中的各個彈性連接相互獨立，則根據式（2）可將連接子結構C 的剛度矩陣KC寫為：

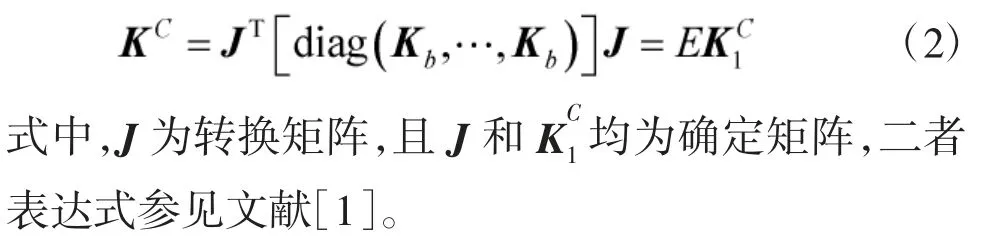
此外，由于空間梁單元只有界面結點自由度而無內部結點自由度，故彈性連接的假設模態集φC為：

基于上述分析結果，可獲得整體結構的質量矩陣M、剛度矩陣K和模態矩陣分別如下形式：

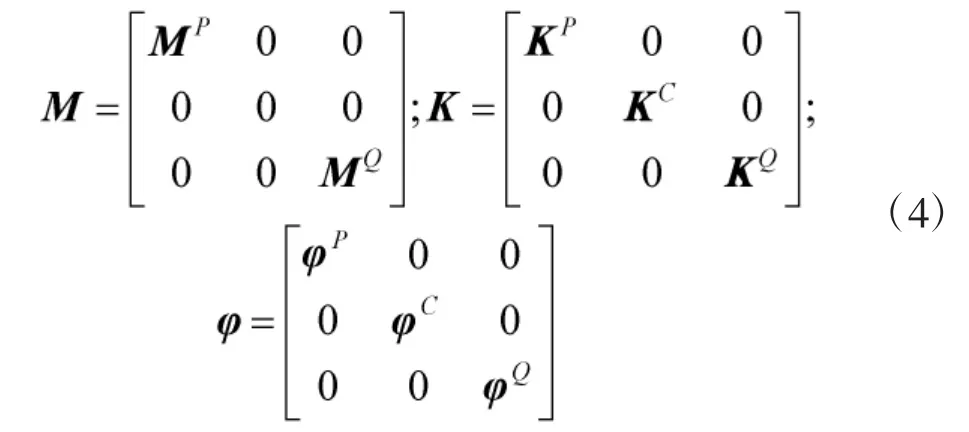
設整體結構的位移列向量為X，即：

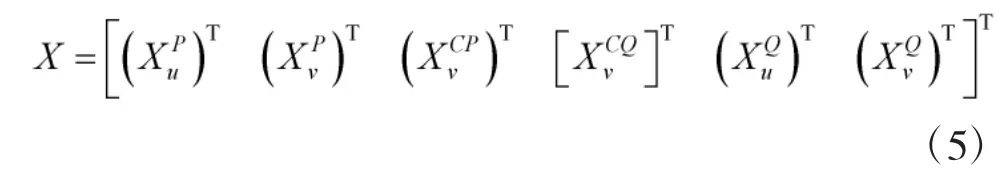
引入界面位移協調條件為：

式中，LP和LQ為坐標旋轉變換矩陣。對式（4）～式（7）進行整理可得：

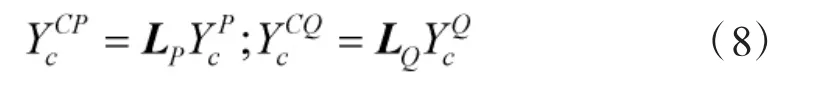
根據式（8）引入矩陣T對模態坐標Y 進行變換，如下所示：

式中，模態坐標Z 中各分塊元素相互獨立。與此同時，可得對應的模態參數矩陣分別為：

綜上所述，基于CMS 建立的如圖1 所示整體結構自由度縮減后的振動方程為：

則由瑞利商公式可得圖1 所示整體結構的第i階角頻率ωi為：

式中，Φi為式（11）所示振動方程的第i 階模態矩陣，矩陣K1和K2均為確定矩陣，二者的表達式分別為：

2 考慮彈性連接的結構頻響函數

考慮彈性連接的FBSM 是基于廣義導納方法推導獲得，而在廣義導納方法的推導過程中要求把所有的子結構等效成一個子結構系統來進行處理，故由文獻［20］可知，可利用圖3 所示示意圖對考慮彈性連接的FBSM 進行推導。

圖3 考慮彈性連接的頻域子結構方法的推導示意圖

圖3 中，頂標“-”和“～”為子結構系統和彈性連接，b 和c 為界面節點自由度，a 為內部節點自由度。據此可知，子結構系統的彈性連接的阻抗矩陣和頻響函數矩陣為：

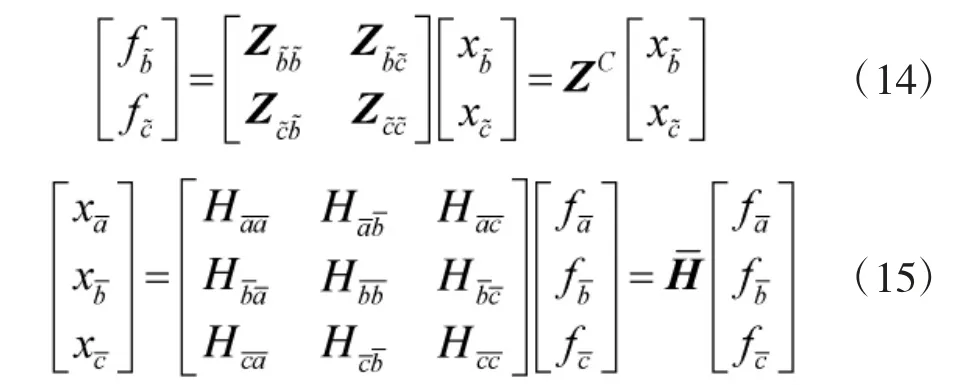
式中，x 和f 分別為響應和激勵列向量，H 和Z 分別為頻響函數和阻抗矩陣，H 為子結構系統的頻響函數矩陣，ZC為彈性連接的阻抗矩陣。假設彈性連接的阻尼為瑞利阻尼，且考慮到MC=0，則可得ZC的表達式為：

式中，j 為虛數單位，β 為瑞利阻尼比例系數。

由于子結構綜合前后其內部結點自由度未發生改變，則有：

引入考慮彈性連接的位移協調和力平衡條件如下：

整理式（14）、式（17）和式（18）可得：

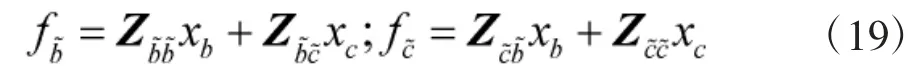
整理式（15）、式（17）和式（18）可得：

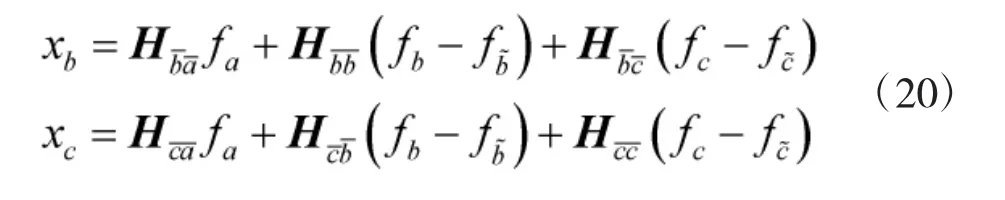
將式（20）代入式（19）并寫成矩陣形式可得：

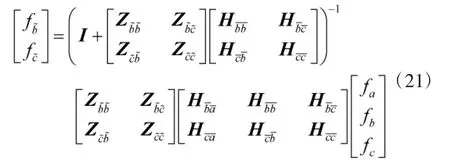
此時，將式（17）、式（18）和式（21）代入式（15），并進行整理即可獲得考慮彈性連接整體結構的頻響函數矩陣H：

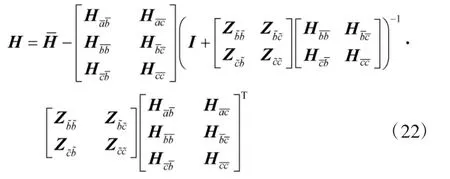
上述即為考慮彈性連接FBSM 的推導過程及結果。此外，文獻［25-26］指出，若上式中的求逆矩陣為奇異矩陣，可利用奇異值分解方法對其進行處理，從而提高該方法的適用性。

3 考慮區間彈性連接的結構動力學特性

本研究將空間梁單元的彈性模量E 和比例阻尼系數β，設成區間參數以模擬彈性連接的區間不確定性。對區間參數的基本概念進行簡單介紹，設G為區間參數，可寫成如下形式：

式中，Gx和Gs分別表示區間參數G 的區間下限和上限。此時，根據IFM 可將區間參數G 寫成其區間中心值Gc與區間因子Gi乘積的形式，即：

上式中，Gc和Gi的表達式分別為：

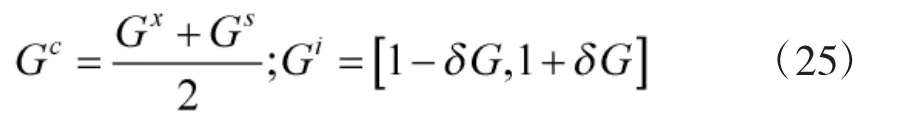
式中，δG 為區間參數G 的相對不確定量，其表達式為：

式中，ΔG 為區間參數G 的區間半徑，其表達式為：

故由上述可得：

3.1 考慮區間彈性連接的結構固有頻率

式（12）所示固有頻率的表達式中，除彈性模量E 外，Φi也為區間參數，故可將Φi寫成其區間中心值與區間因子乘積的形式，即：

將式（28）和式（29）代入式（12）并進行整理可得：

式中，ξi的表達式為：

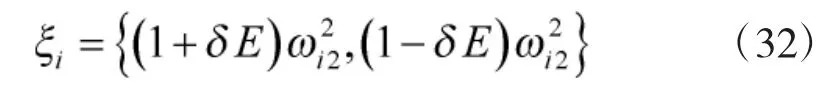
3.2 考慮區間彈性連接的結構頻響函數

記e=1+jωβ，則e 也為區間參數，即可寫為：

將式（2）、式（28）和式（33）代入式（16）并整理可得：

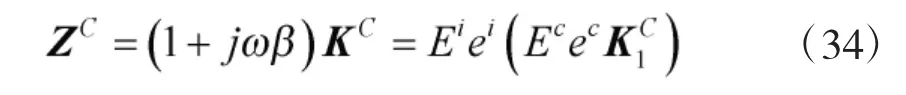
將式（34）代入式（22）并整理可得：

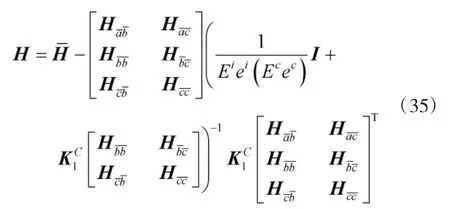
此時，根據區間分析方法，可得考慮區間彈性連接的結構頻響函數幅值的區間下限和區間上限分別為：

式中，ξ 的表達式為：

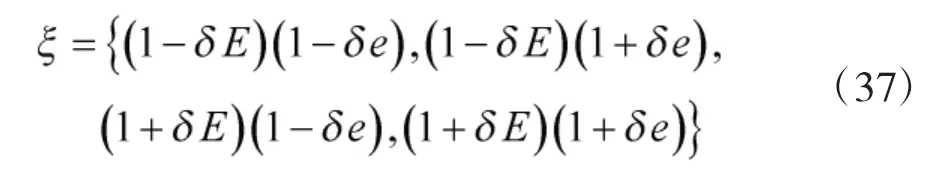
4 仿真驗證

為了驗證CMS-IFM 和FBSM-IFM，本研究設計了一個梁結構，如圖4 所示。其中，矩形截面梁P 和Q 的材料參數和幾何尺寸相同，阻尼均為瑞利比例阻尼，兩根梁的參數均為確定參數；C 為兩根參數相同的圓形截面梁，其密度設為0，彈性模量和瑞利阻尼比例系數為區間參數，用來模擬區間彈性連接。利用空間梁單元對梁結構進行單元劃分，并定義單元屬性［27-28］，其中，表1 為連接子結構C 的單元屬性，表2 為主子結構P 和Q 的單元屬性。

圖4 梁結構示意圖

分別利用CMS-IFM 和FBSM-IFM 對梁結構的固有頻率和指定結點頻響函數幅值的區間下限和上限進行了計算，同時利用Monte-Carlo 模擬方法開展了相應計算。在利用CMS-IFM 計算時，保留子結構P 和Q 的前30 階主模態參加模態綜合；在利用FBSM-IFM 開展計算時，選用子結構P 和Q 的前30 階模態進行各自頻響函數矩陣的計算，計算方法參見文獻［27］。在利用Monte-Carlo 模擬方法進行計算時，假設兩個區間參數E 和β 在其分布區間內都呈均勻分布，然后生成5 000 個樣本，并分別代入整體結構的有限元模型中進行計算（即共計算5 000次），最后從5 000 個計算結果中選取固有頻率和頻響函數的區間下限和上限。

表1 連接子結構C 的單元屬性

表2 主子結構P 和Q 的單元屬性

表3 給出了利用CMS-IFM 和Monte-Carlo 模擬方法對算例結構固有頻率區間下限和上限計算結果的對比情況。圖5 給出了利用FBSM-IFM 和Monte-Carlo 模擬方法，對算例結構中兩個結點u 和v 之間3 個平動方向頻響函數幅值區間下限和區間上限的計算結果對比情況。

表3 中，CIx、CIs和MCx、MCs分別為CMS-IFM和Monte-Carlo 模擬方法對固有頻率計算結果的區間下限和上限，εx和εs分別為CMS-IFM 對固有頻率區間下限和上限的相對計算誤差。不難發現，CMS-IFM 對固有頻率區間下限和上限的相對計算誤差分別在±0.586 %和±0.628 %以內，表明CMS-IFM 在保證計算精度的前提下，可有效提升計算效率。

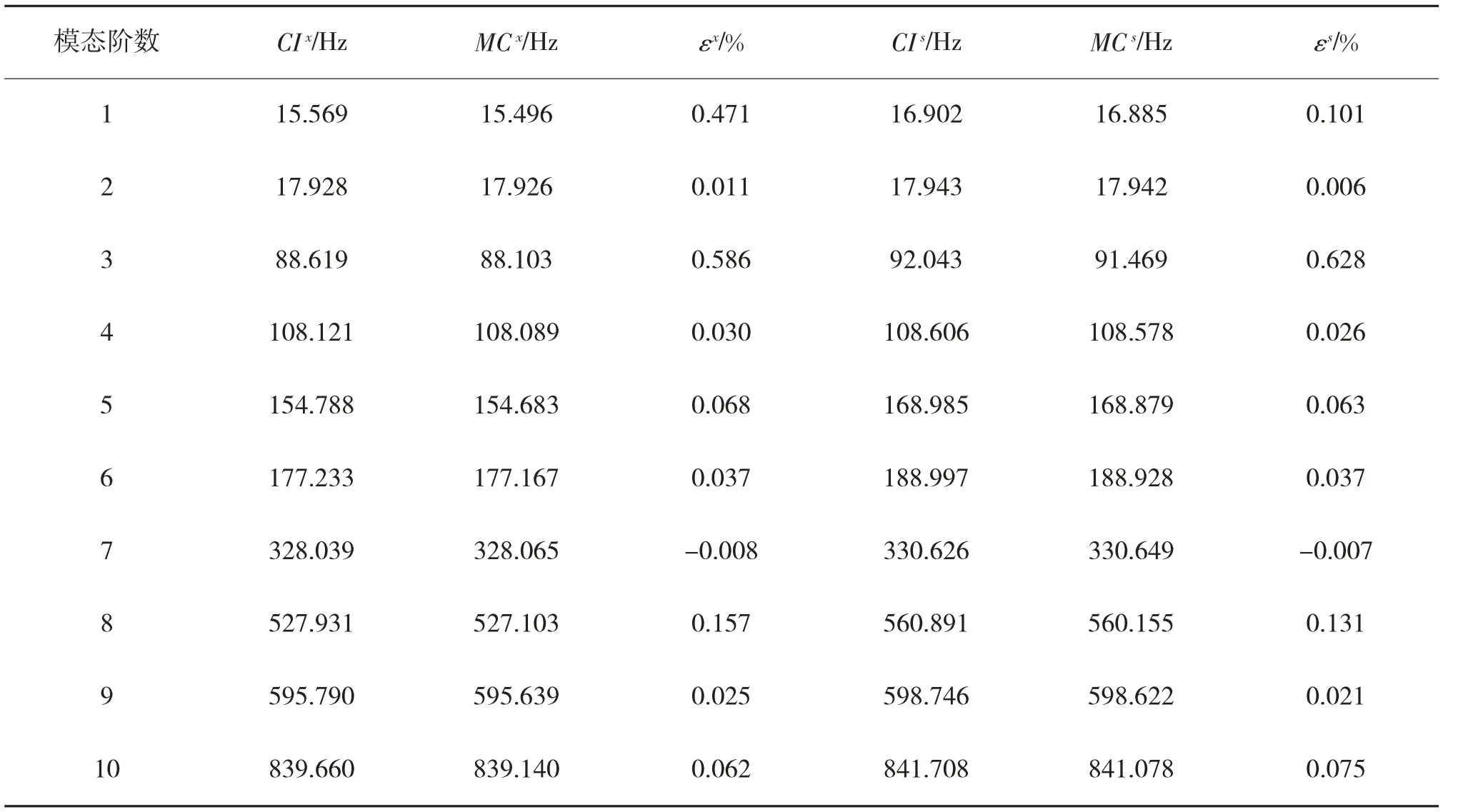
表3 CMS-IFM 和Monte-Carlo 模擬方法計算結果

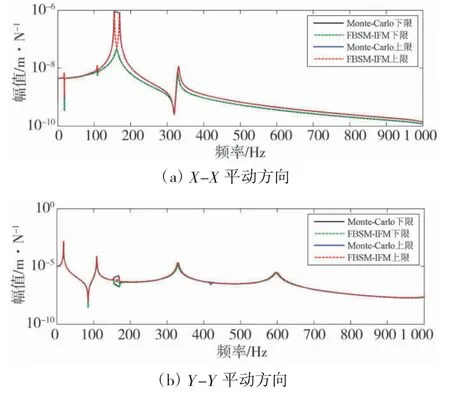
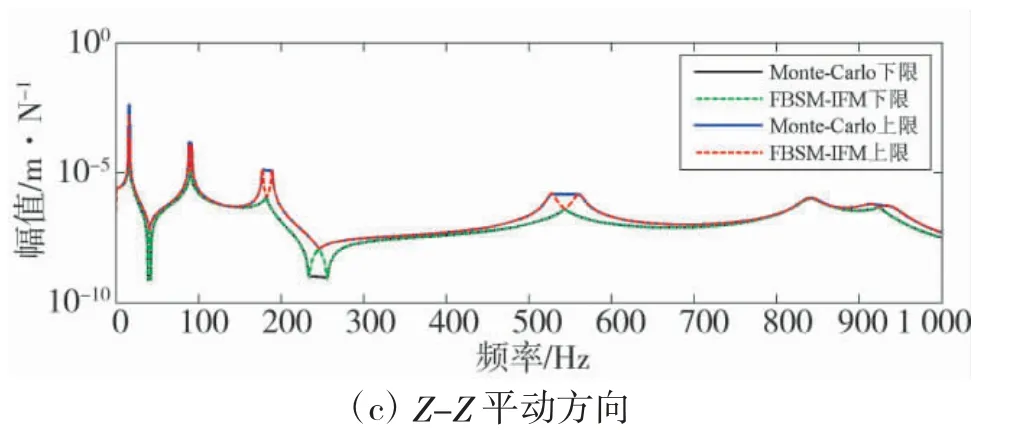
圖5 不同平動方向兩種方法計算結果的對比情況

由圖5 可知，兩種方法對圖3 所示算例結構頻響函數幅值區間下限和區間上限的計算結果吻合程度良好，驗證了FBSM-IFM 的正確性。

5 結論

1）筆者利用具有區間彈性模量和比例阻尼系數的零質量空間梁單元模擬復雜結構中的區間彈性連接，基于CMS 和FBSM 對考慮彈性連接的結構固有頻率和頻響函數進行了推導，并結合IFM 提出了計算考慮區間彈性連接結構動力學特性的高效方法，即CMS-IFM 和FBSM-IFM。

2）該方法基于IFM 綜合考慮彈性連接結構的區間不確定性，不僅可以單獨考察某一區間不確定參數對結構動力學特性的影響，而且可以有效地規避區間參數，按照確定參數進行處理時可能得到矛盾的或很不合理的結果的問題。

3）算例仿真結果表明：與Monte-Carlo 模擬方法相比，CMS-IFM 和FBSM-IFM 在保證計算精度的同時，均可大幅提升計算效率，所得的結論具有較高的理論研究和工程應用價值。