蜂窩夾層結構材料在簇絨地毯織機主軸空間降噪中的應用

王皓輝， 徐 洋， 盛曉偉

(東華大學 機械工程學院， 上海 201620)

簇絨地毯織機噪聲工況異常復雜，且其主軸為主要噪聲源。強烈的環境噪聲會對紡織工人的身心健康造成嚴重危害。為改善簇絨地毯織機工作空間的聲學環境，在其表面安裝降噪結構是最直接有效的措施。

蜂窩板作為一種特殊的復合材料，其具有強度高、剛度高、質量輕的特點，同時擁有良好的隔聲性能。嘗試利用蜂窩夾層結構控制主軸噪聲傳播，對紡織領域的聲學控制研究具有一定的積極作用。簇絨地毯織機主軸結構復雜，其振動噪聲信號一般表現為多種復雜的非穩態信號和少數穩態信號的組合形式，即入射到蜂窩板表面的是方向分布均不確定的復雜聲波，因此考慮蜂窩夾層結構的聲學特性是研究簇絨地毯織機主軸空間降噪的一個重要前提。

迄今為止，國內外許多學者從理論、數值、試驗等方面對蜂窩板的聲學性能展開研究。Ruzzene[1]研究周期分布的蜂窩梁夾層和衍架層的聲輻射，并對其進行詳細闡述。Wang等[2]在蜂窩板的模型上采用傳遞矩陣法分析計算板件的聲傳輸損失，并與試驗結果進行對比。Wu等[3]等建立了無限大正交異性夾層板的振動控制方程，雖然其解析形式便于應用，但是未考慮板件夾層的剪切剛度。Zhou等[4]應用統計能量分析法研究復雜夾層結構-泡沫填充蜂窩夾層板的傳聲損失。Jonza等[5]發現，增加蜂窩芯層中面板的空洞和凹陷將增大蜂窩夾層板的傳聲損失。Gibson等[6]采用理論方法給出了蜂窩材料的等效參數公式，雖然其解析形式便于應用，但在推導過程中僅考慮蜂窩板的彎曲變形，而未考慮蜂窩胞元壁板的伸縮變形，因此該公式存在一定誤差。

綜上所述，針對蜂窩板聲學性能的研究主要集中在板件的隔聲問題上，且研究者基本都對模型進行了簡化。本文運用聲學無限元法，通過引入蜂窩板的鋪層等效有限元模型建模方法[7]并考慮芯層剪切剛度，以DHU-2型簇絨地毯織機主軸為例，建立主軸與蜂窩板封閉/半封閉的內聲場，并對測點處的聲壓進行分析計算。

1 考慮剪切剛度的蜂窩板建模原理

在多數工程應用中，蜂窩板由上下蒙皮和中間的蜂窩芯子構成，蒙皮與芯子采用黏結劑進行連接，具體結構如圖1所示。蜂窩板通常都按照等效板方法進行建模，即建立與蜂窩板相同尺寸的Shell單元，并輸入等效參數。通過引入鋪層等效建模方法[7]，考慮蜂窩胞元伸縮變形以及芯層剪切剛度，以準確計算蜂窩板的等效參數。

圖1 蜂窩板的結構示意圖Fig.1 Schematic diagram of honeycomb panel

1.1 蜂窩板振動理論模型

蜂窩板的橫向剪切剛度對夾層板傳聲特性有顯著的影響[8]，目前多數等效板理論均忽略了蜂窩芯層的剪切剛度。本文根據Reissner-Mindlin剪切變形理論，對板件提出4點假設：(1)面板厚度與整體蜂窩板厚度相比很小，可視為薄膜(殼單元)；(2)蜂窩芯層材質較軟，僅承受橫向剪切應力；(3)彎曲前垂直于夾層板中面的法線在彎曲變形后仍保持直線，但不垂直于撓曲后的中面；(4)沿夾層板厚度方向無正應變產生。

在上述假設條件下，蜂窩夾層板的自由振動控制方程組可表示為

(1)

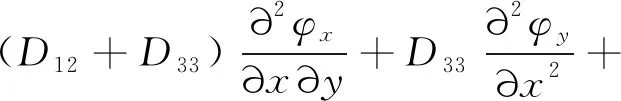
(2)

(3)

式中：φx、φy、w為廣義位移；Dij(i,j=1, 2, 3)為蜂窩板的彎曲剛度；Cxz、Cyz為芯層剪切剛度；ρ為板件的等效面密度。為簡單起見，邊界條件按照式(4)和(5)設置成為四邊簡支。

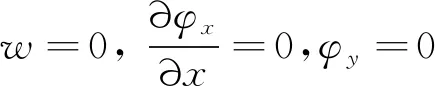
(4)

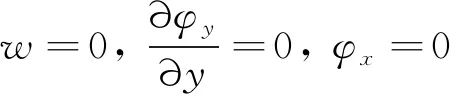
(5)

滿足上述邊界條件的控制方程的解具有如式(6)[3]所示形式。

β=Asin(km1x)sin(km2y)ejωt

(6)

式中：km1=m1π/a、km2=m2π/b；m1、m2為模態序數；ω為板件固有角頻率。將式(6)代入式(1)～(3)，得到板件固有角頻率為

(7)

若不考慮剪切剛度的影響，即Cyz→∞，Cxz→∞，式(7)變為

(8)

不考慮芯層剪切剛度是指將芯層剪切剛度定義為無窮大即沒有剪切變形，而在有限元軟件中無法準確計算忽略剪切剛度情況下的板件固有頻率，因此只能通過理論進行計算。

將考慮/不考慮剪切剛度的板件固有頻率計算結果與文獻[9]的試驗結果進行對比，結果如圖2所示。忽略芯層剪切剛度將使得板件固有頻率的計算結果產生較大誤差(300～800 Hz)，因此芯層剪切剛度不能忽略。

圖2 考慮/不考慮剪切剛度的模態計算 結果與文獻[9]的試驗結果比較Fig.2 Comparison of the results of modal calculations with/without considering shear stiffness with the experimental results from literature[9]

1.2 傳聲理論模型

建立蜂窩板的傳聲理論模型，平面聲波以入射角θ、方位角Ψ入射到板件表面，pi、pr、prad、pt分別為入射聲壓、反射聲壓、輻射聲壓和透射聲壓，如圖3所示。

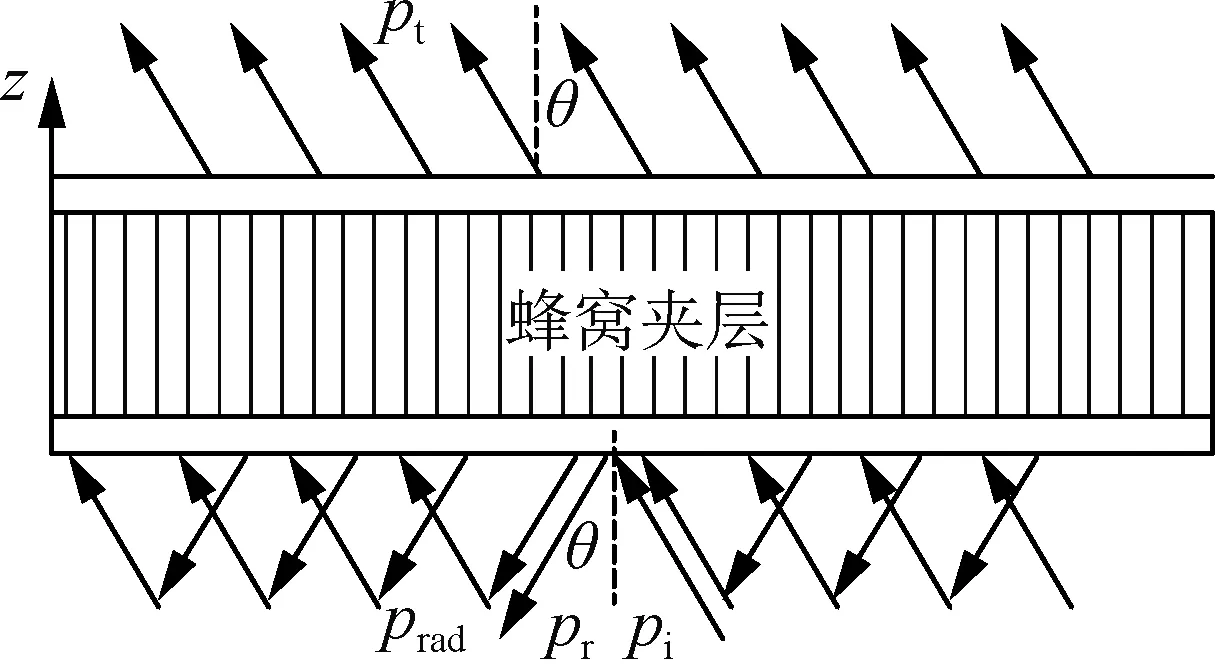
(a) 局部圖

(b) 整體圖

聲學激勵本質上是作為一種力載荷施加在夾層板表面的，對式(3)進行變換可得：

(9)

結合式(1)、(2)、(9)可得：

(10)

(11)

由于蜂窩板的面板是各向同性且對稱的，因此D11=D22=D12+2D66，結合式(9)～(11)可得：

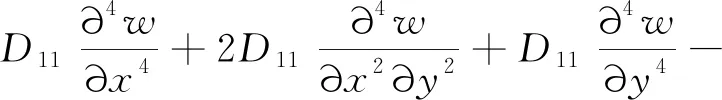
(12)

聲壓[10]可表示為

(13)

式中：δ為聲波圓頻率；P為聲壓幅值；k為聲波波數。載荷q為

q=pi+pr+prad-pt=2(Pi-Pt)ej(δt-kxsin θ)

(14)

夾層板水平面的豎直位移w為

w=Wej(δt-kxsin θ)

(15)

式中：W為豎直方向的位移幅值。將式(13)和(14)代入(12)可得：

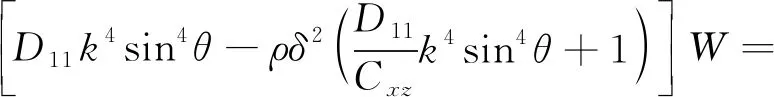
(16)

聲傳輸系數表示為

(17)

將聲傳輸損失的理論計算結果與文獻[10]的試驗結果進行對比，如圖4所示。由圖4可知，在低頻范圍(250～400 Hz)內，理論結果與試驗結果存在一定差距，其主要原因是計算過程中將蜂窩芯層等效為各向異性參數層，這樣的等效在低頻階段會對計算結果產生影響。即使如此，傳聲理論模型結果仍優于其他忽略剪切剛度理論的預測結果。

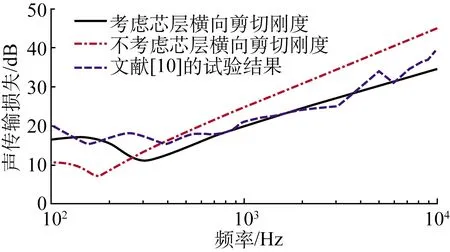
圖4 理論結果與文獻[10]的試驗結果對比Fig.4 Comparison of theoretical results and experimental results of literature[10]

2 具體算例

以DHU-2型簇絨地毯織機主軸(見圖5)為例，建立主軸與蜂窩板的聲場耦合有限元模型，如圖6所示。將蜂窩板沿著機器外表面固定并與主軸組成半封閉的聲場。測點位于正對機器表面的1.35 m、距離地面1.25 m處。蜂窩板的安裝示意圖如圖7所示。將第1節計算的等效參數(包括芯層剪切剛度、彎曲剛度等)輸入有限元模型中，以實際測量的主軸振動速度信號為激勵，對比有、無蜂窩板情況下測點聲壓的響應曲線。

圖5 簇絨地毯織機主軸Fig.5 Spindle of tufted carpet loom

圖6 聲場示意圖Fig.6 Schematic diagram of sound field

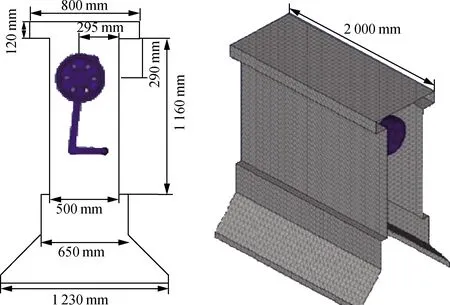
圖7 蜂窩板安裝示意圖Fig.7 Schematic diagram of honeycomb board installation

采用有、無限元法進行聲學模擬時對網格尺寸有特殊性要求，即線性有限元的最大單元通常要小于最高計算頻率點處波長的1/6。簇絨地毯織機主軸振動信號基本在1 000 Hz以下，且800～1 000 Hz的振動信號基本為零[11]。因此單元最大尺寸小于60 mm。測點聲壓對比如圖8所示。

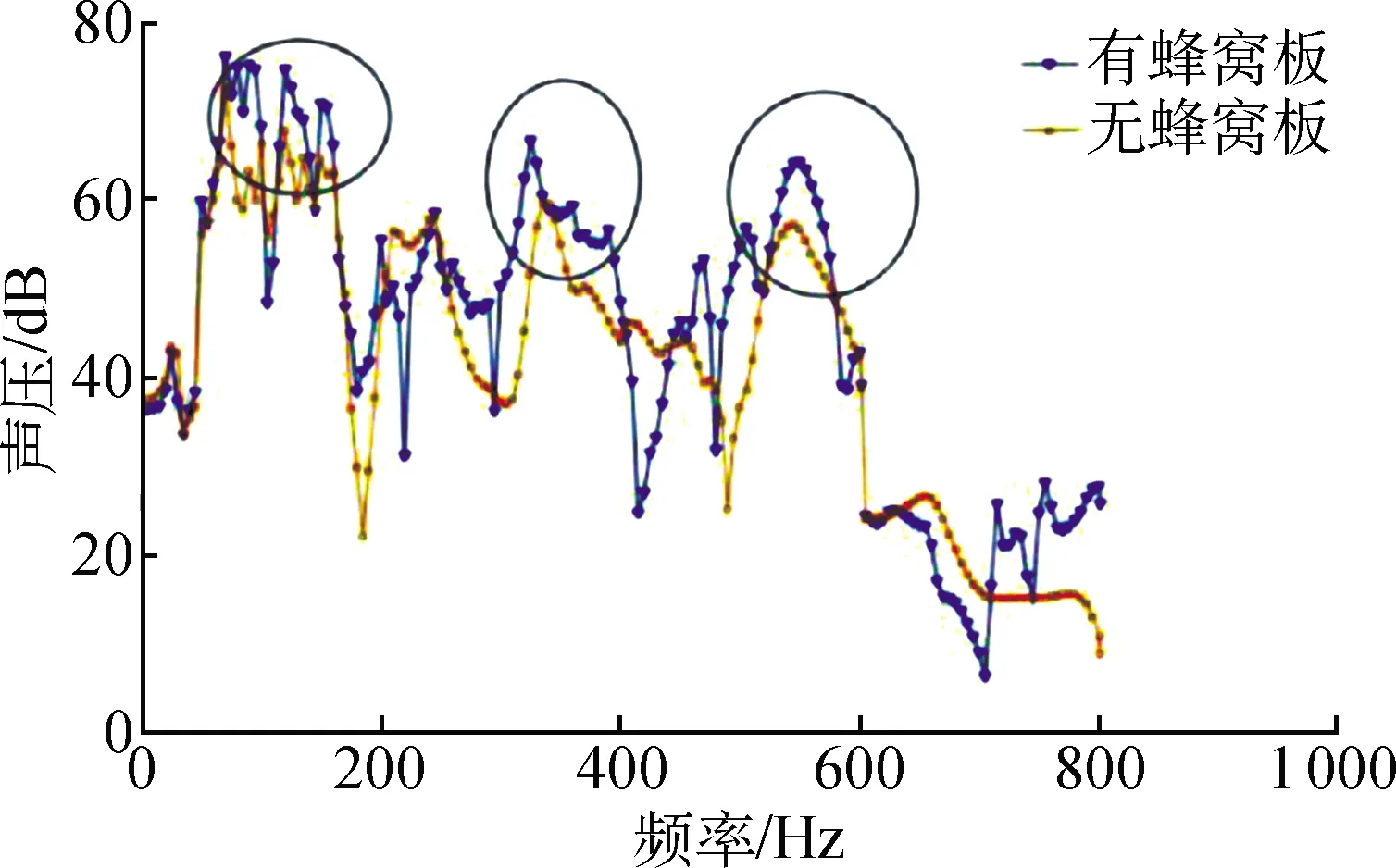
圖8 測點聲壓對比圖Fig.8 Comparison chart of sound pressure at monitoring points

由圖8可以看出，測點聲壓在有、無蜂窩板阻擋情況下的差別較大，但聲壓曲線整體變化趨勢基本相同，波峰分別出現在70、 90、 120、 325、 550 Hz處。在低頻階段，有蜂窩板阻擋時的聲壓比無蜂窩板時大，這是因為，考慮簇絨地毯織機的實際工況，蜂窩板與主軸組成的是半封閉聲場，即左、右兩邊并沒有用蜂窩板完全封閉，這就導致被阻擋的噪聲被“擠壓”到左右兩邊后“并發”，使得測點聲壓發生疊加。由此可見，單一的蜂窩板屬于隔聲材料，并不具備吸聲性能(即無法消除聲能總量)，只能用于外聲場的降噪，對于內聲場則需要添加吸聲材料以進一步吸聲、吸能。

3 胞元尺寸與測點聲壓函數關系

對于蜂窩板這類多孔板材，其力學/聲學性能都是通過影響板件的剛度、質量而起作用的。但是相比板件其他設計參數如芯層厚度、面板厚度等，胞元尺寸對板件的質量與剛度影響最大。當胞元尺寸趨向于無窮小時，蜂窩板將變成一塊實體板；當胞元尺寸趨向于無窮大時，蜂窩板將變成中空板。目前大部分關于蜂窩板優化方面的文獻未將胞元尺寸作為參數進行研究，其原因是胞元尺寸作為參數有其特殊性，即其每一次改變都會涉及蜂窩芯子的重新布局，相當于每一次迭代都需要重新建模[12]。

將鋪層等效有限元模型構建方法引入蜂窩板的聲學建模中，鋪層等效有限元模型的材料參數作為變量。由文獻[12]可知，等效參數公式是線性可逆的，胞元尺寸的每一次變化都會帶動鋪層板材料參數的變化，由此可以間接得出胞元尺寸與測點聲壓之間的函數關系，可為今后的蜂窩板優化提供一定的參考。

測點聲壓(聲壓級)與多參數方程可簡單地表示為

P′i=P′(h，l，g，d)

(18)

式中：h為蜂窩芯子高度；l為胞元尺寸；d為蒙皮厚度；g為胞元厚度。

對式(18)進行全微分，得到如式(19)所示的方程。

(19)

式(19)可近似表達為

(20)

式(20)表明，測點聲壓的變化是由板內部一個或多個參數變化引發的結果。

根據圖8可知，測點聲壓曲線圖波峰分別在70、 90、 120、 325、 550 Hz處。本次僅研究胞元尺寸與聲壓的關系，因此保持其他參數不變，而胞元尺寸從1.0 mm到 10.5 mm每隔0.5 mm取點進行計算，共選取20個點，將計算結果導入MATLAB軟件繪制出各個波峰頻率的函數關系圖并擬合出函數，如圖9所示。

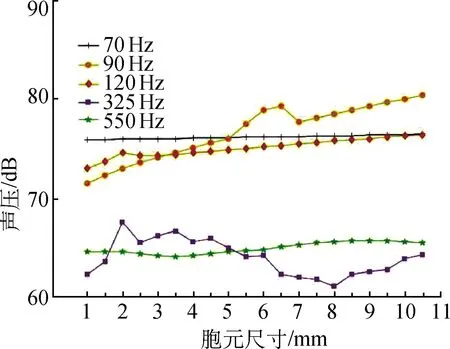
圖9 聲壓與胞元尺寸關系圖Fig.9 Sound pressure according to cell size

參數常數項的確定依賴于一定區域范圍內參數與頻率的關系式，對于同一范圍內的數據點可能存在不止一種函數表達式，但這些函數表達式在同一區域所表達的參數意義是相同的，因此在數據點擬合的方程中只需要選擇形式簡便連續性好的方程即多項式形式P′i=a1l5+a2l4+a3l3+a4l2+a5l+a6，常數項如表1所示。

根據圖9可知：當增大胞元尺寸時，70 Hz處的聲壓變化并不明顯，變化范圍在1 dB以內；在90、 120、 550 Hz處，聲壓隨著胞元尺寸的增大而不斷增大；在325 Hz處，聲壓初始變化最明顯，但隨著胞元尺寸的增大逐漸趨于平穩。總體而言，胞元尺寸在90、 120、 325、 550 Hz處對測點聲壓的影響要大于70 Hz處對測點聲壓的影響。這主要存在兩方面原因：一方面當聲波以一定角度投射到板件表面，且聲波的頻率與板件固有頻率一致時，板件的運動與空氣中聲波的運動達到高度耦合，聲能量大幅穿過板件。由文獻[12]的研究結果可知，在一邊固支約束條件下蜂窩板固有頻率93.82和553.12 Hz正好與圖9中的波峰位置90和550 Hz對應。另一方面，主軸的振動聲能主要集中在110～400 Hz處[13]，單純的蜂窩板并沒有吸聲性能，本質上屬于隔聲結構，在半封閉聲場中，聲能沒有減少的情況下會發生聲壓疊加。

表1 常數項與頻率關系

4 結 論

(1) 針對簇絨地毯織機主軸振動噪聲信號的不確定性，將蜂窩夾層材料引入主軸降噪過程中，基于Reissner-Mindlin夾層板理論的振動控制方程，建立蜂窩夾層板振動理論模型和聲壓激勵作用下的聲振耦合理論模型，并通過數值分析的方法揭示了忽略剪切剛度對板件頻率、聲傳輸系數的影響。

(2) 將鋪層等效有限元法引入聲學建模中，建立主軸與蜂窩夾層板的聲場耦合有限元模型，為簇絨地毯織機主軸工作空間聲場的進一步吸聲優化提供方法。

(3) 基于鋪層等效有限元模型所建立蜂窩胞元尺寸與測點聲壓在70、 90、 120、 325、 550 Hz處的函數關系，可直觀地反映胞元尺寸對測點聲壓的影響程度，有望為準備開展基于蜂窩夾層材料的簇絨地毯織機主軸工作空間降噪相關工作提供一定的借鑒和參考。