Lie transformation on shortcut to adiabaticity in parametric driving quantum systems?
Jian-Jian Cheng(程劍劍), Yao Du(杜瑤), and Lin Zhang(張林)
School of Physics and Information Technology,Shaanxi Normal University,Xi’an 710119,China
Keywords: shortcut to adiabaticity,parametric driving,Lewis–Riesenfeld invariants
1. Introduction
The quantum adiabatic technique is one of the promising strategies for quantum computation based on quantum adiabatic theorem.[1]“Shortcuts to adiabaticity” (STA) are control protocols that take quick routines to the same populations,or even the same final states reached by the slowly adiabatic processes.[2]A motivation to apply STA methods to quantum systems is to manipulate quantum evolution with fast coherent dynamics of high fidelity.[3]Now STA has become a typical technique in preparing or driving internal and external states in atomic,molecular,optical,and solid-state physics.[4–7]
Due to the time-consuming problem of adiabatic parametric driving, two equivalent strategies for STA engineering developed so far. One is the transitionless quantum driving method,[8–10]the other is the invariant-based inverse engineering technique.[11]The basic idea of transitionless quantum driving is to introduce an auxiliary interaction1(t)to the original Hamiltonian0(t),


where

is the adiabatic states starting with|n(0)〉without the geometric phase for theoneparametric driving system. The reverse auxiliary interaction1is given by Berry’s formulation[12]
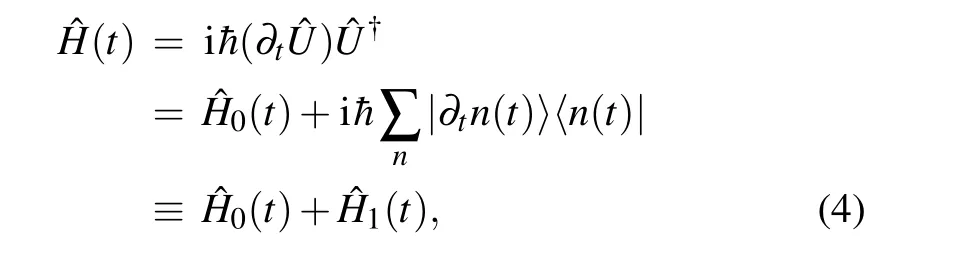
where the auxiliary Hamiltonian1(t) is nondiagonal in the basis of|n(t)〉, and it requires a full knowledge of spectral properties of the instantaneous Hamiltonian0(t). However,in most practical cases,the auxiliary interaction calculated by instantaneous eigenstates is hard to carry out. Now we give an alternative method to do STA in a general parametric driving system with Lie transformations. Starting from a general Hamiltonian of harmonic oscillator,[13]three independent generators can be defined by

and we can introduce three independent unitary transformations based on SU(2)by[14]
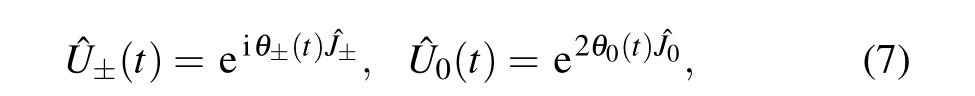
where the transformation parametersθ±(t) andθ0(t) are piecewise continuous real functions defined within a control time interval[0,τ]. The above quantum transformations±(t)and0(t) correspond to classical canonical transformations called rotations and squeezing,respectively. These unitary operators maintain the phase volume of the transformed state and constitute our“Lie transformations”method to construct adiabatic Hamiltonian for STA designs.
2. Parametrically driven quantum harmonic oscillator
The first system,which receives much attention due to its fundamental and practical significance, is the parametric harmonic oscillator with fast harmonic trap expansions. It can be applied to the cold atoms involving an adiabatic tuning of the system after a cooling phase.[15]For a parametric driven harmonic oscillator,we consider the Hamiltonian

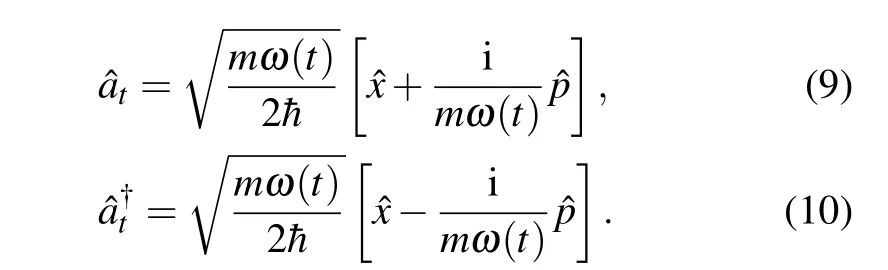
Since the frequency depends on time,the instantaneous ladder operatort(?t)will create(annihilate)different instantaneous states at different times adapting to different frequencies.
Now, we consider an STA control fromt= 0 toτby Lie transformations. In this case, we first introduce squeezing transformation as

and the instantaneous states of the final system satisfy

A direct substitution of Eq. (12) into Eq. (4) yields the adiabatic Hamiltonian
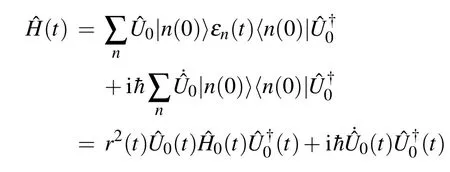

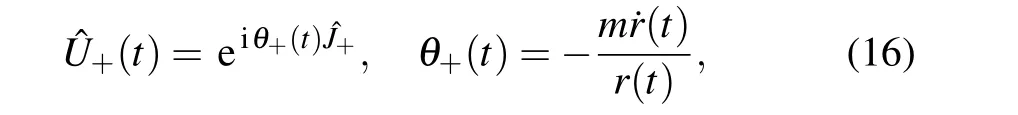
which continues to transform Hamiltonian(t)into
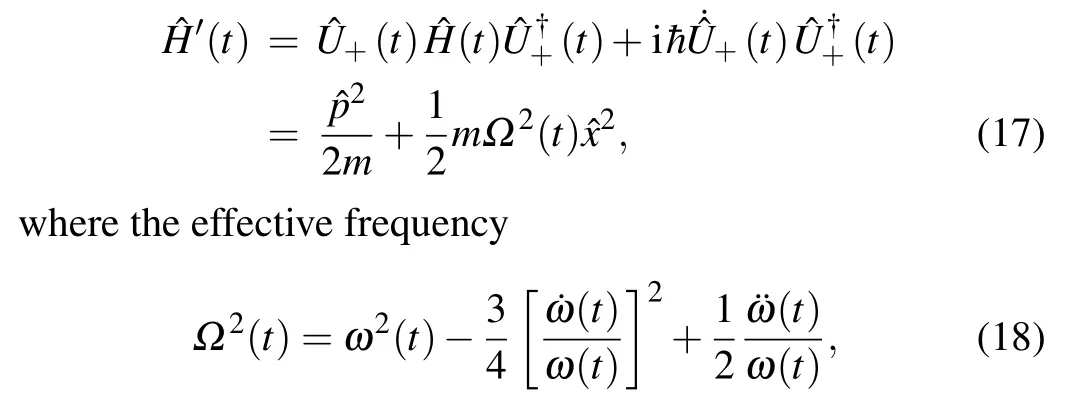
which can be easily realized in the practical control.[17]The new Hamiltonian'(t)has the same structure as Hamiltonian0(t) but with different time-dependent frequencies, which can be conducted by magnetic and optical fields in the cold atom experiments for a time-varying trapping.
Under the above successive transformations, the time evolution of the initial state|n(0)〉is mapped to

which generates a similar final state of an adiabatic process evolving slowly from0(0)to0(τ)if the control frequency?(t)meets the boundary conditions

The above conditions lead to

The zero of the first time-derivative means|Φn(0,τ)〉=|ψn(0,τ)〉and the zero of the second one implies'(0,τ)=0(0,τ).
In order to design the frequency?(t) to meet Eq. (21),a polynomial ansatz of time function forω(t) is often utilized,[11]
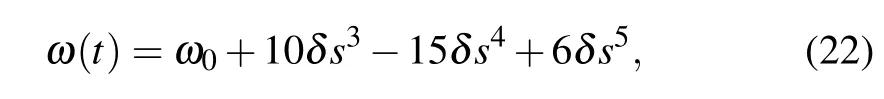
whereδ=ωτ ?ω0ands=t/τ.The trajectories with different control times are displayed in Fig.1.

Fig. 1. The adiabatic drivings of the trap frequency ?2(t) changing from ω0 =2π×250 Hz to ωτ =2π×25 Hz, displayed for three different control times τ =30 ms(red solid line),τ =10 ms(blue dashed line)and τ =5 ms(green dot-dashed line).
We can see that?2(t)may become negative during some time intervals if the control process is very fast (green dotdashed line), driving the potential to an expulsive parabola.These state-independent shortcut controls are ideal for maximal robustness owing to no excitation in the final state but allowing for excitations in the intermediate. With Lie transformations,it is convenient to verify that the above STA design is equivalent to the Lewis–Riesenfeld(LR)invariant method.[11]If we set the total transformationI(t)≡+(t)0(t),then the new adiabatic Hamiltonian'(t)is obtained by

where the LR invariant is defined by
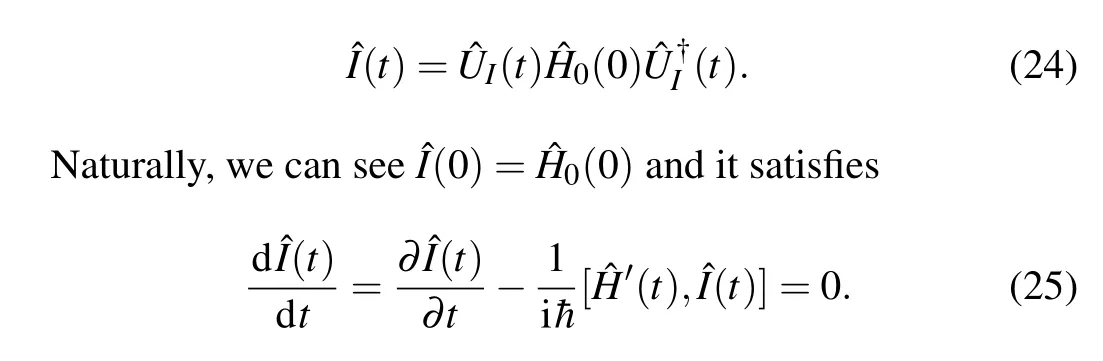
From Eq.(26),we can find that the eigenvectors of(t)are
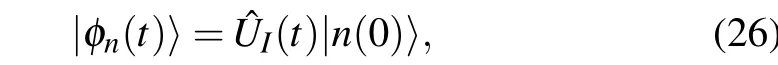
which satisfy

As the new Hamiltonian of Eq. (23) must be equivalent to Hamiltonian of the system0(t) at the initial and final times for STA controls,the boundary conditions will be

These new constraints can naturally recover Eq.(21)and make1(t) vanish at the initial and final times. It should be noted that the transformed Hamiltonian'(t) we found here is just the Hamiltonian for LR dynamical invariant(t). This is the essence of invariant-based inverse engineering and our method avoids the difficulty for constructing dynamical invariants(t)for a given system.[18]
We can conclude that, referring to the previous approaches about harmonic oscillator expansions,the Lie transformation method proposed here provides a solid algebraic framework for STA controls, which consistently introduces auxiliary counterdiabatic Hamiltonian without resorting to classical analog of dissipationless driving.[19]
3. Power-law trap
In the Lie algebraic framework,a generation to other trapping potentials is straightforward. We apply our trick on a free particle inside an expanding one-dimensional box (quantum piston)described by[20]

which defines an infinite square well with a moving boundary atx=L(t). If the well expansion is slow enough to follow adiabatic theorem,the exact solution can be expressed as

Since the width of box depends on time, a squeezing transformation can be introduced

with an initial widthL(0)≡L0. In the coordinate representation, the squeezing means increasing the wavelength of the free particle and reducing its momentum,which gives

The above Hamiltonian can be used to control quantum gas of non-interacting particles confined in an expanding box with the initial populations sampled microcanonically. The gas will remain a uniform distribution for an arbitrary expanding boundaryL(t)because the auxiliary term in Eq.(37)suppresses shock waves(excitations)by uniformly expanding the gas.[21]
This transformation technique can be easily generalized to all even-power-law potentials:[22]

where?n(x)are the wavefunctions of Hamiltonian with a onedimensional potential of Eq. (38). Substituting Eq. (39) into Eq.(4),we can find the controlling adiabatic Hamiltonian

The above new Hamiltonian introduces an auxiliary potential




Fig.2. Shortcuts to adiabaticity by adiabatic driving,for an expansion factor L(τ)=2 with different power-law traps. The exponent values of auxiliary potentials correspond to harmonic oscillator (red solid line),a quartic trap potential (blue dashed line), and an expanding quantum piston(green dot-dashed line).
4. Conclusion
A unified algebraic framework is developed to design shortcuts to adiabaticity in both transitionless quantum driving and invariant-based inverse engineering method. We demonstrate that the two approaches are mathematically equivalent and share a common physical ground with Lie transformations, and provides a universal method to design STA for the general time-dependent parametric driving systems. It removes the demanding requirement to diagonalize the Hamiltonian of the system in the transitionless driving method,and the difficulty to find the invariant quantities in the invariantbased inverse engineering technique. The Lie transformation method presents a powerful tool to design STA control in the homogenous power-law trapping system and can neatly combine the invariant-based method with the transitionless driving method by quickly diagonalizing the reference Hamiltonian.In summary, this method provides a deeper insight into STA techniques that can be easily applied to a variety of systems in quantum control problems.
Appendix A: Derivations of squeezing transformation
The squeezing transformation is a unitary operator and it is easy to prove

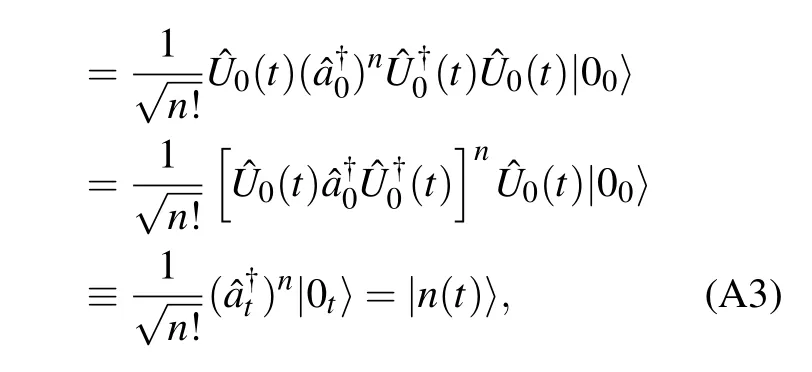
where the vacuum state at timetis defined by|0t〉≡0(t)|00〉.
- Chinese Physics B的其它文章
- Coarse-grained simulations on interactions between spectrins and phase-separated lipid bilayers?
- Constraints on the kinetic energy of type-Ic supernova explosion from young PSR J1906+0746 in a double neutron star candidate?
- Computational model investigating the effect of magnetic field on neural–astrocyte microcircuit?
- Gas sensor using gold doped copper oxide nanostructured thin films as modified cladding fiber
- Exact explicit solitary wave and periodic wave solutions and their dynamical behaviors for the Schamel–Korteweg–de Vries equation?
- Suppression of ferroresonance using passive memristor emulator

