Fractal sorting vector-based least significant bit chaotic permutation for image encryption?

Yong-Jin Xian(咸永錦) Xing-Yuan Wang(王興元) Ying-Qian Zhang(張盈謙)

Xiao-Yu Wang(王曉雨)1, and Xiao-Hui Du(杜曉慧)1

1School of Information Science and Technology,Dalian Maritime University,Dalian 116026,China

2School of Information Science and Technology,Xiamen University Tan Kah Kee College,Zhangzhou 363105,China

Keywords: chaotic image encryption, fractal sorting vector, bit-level permutation, FSV-based LSB chaotic

1. Introduction

Research on image security has gained widespread publicity in recent years.[1–4]With the development of cryptography as an important image authentication tool,image encryption has attracted a great deal of attention.[5,6]The researchers incorporated the chaos technique into image encryption and provided several useful chaotic image encryption studies.[7–17]

Image encryption algorithm based on chaos consists of pixel scrambling and pixel diffusion within the context of the cryptanalysis image encryption scheme of Fridrich.[18]In the design of chaotic image encryption algorithms, bit-level permutation simultaneously realized the pixel uncertainty and pixel diffusion,which enhances the security of image encryption algorithm.[19–22]In Ref. [23], the original image was divided into 8 binary images,then the 8 binary images were encrypted respectively, and then synthesized into a gray-scale encrypted image. In Refs.[24,25],a bit-level permutation approach was implemented to color the image encryption. The pixel-based bit exchange could exert a certain encryption effect,but it would do better with bit-level scrambling based on bit planes. In Ref.[26],the bit in the pixel was scrambled into its neighboring pixel,so that the direction of the bit varied between each plane. In Ref.[27],by applying rank and column encryption to each binary bit plane,the image algorithm realized the bit-level permutation. In Ref.[28],the 8 bits of each pixel were split into the four most important bits on the left and the four least significant bits on the right. The LSBs were independently encrypted. In Ref. [29], the right four bits of each pixel were scrambled separately, while the left four bits were encrypted as a whole part. In Ref.[30],the bit positions of the image’s LSB planes were scrambled, and thus leaving the other planes on the left unchanged.

By analyzing the above-mentioned bit-level permutation methods, they can be divided into two categories: bit permutation on all bit planes and bit permutation on least significant bit planes. The bit permutation on LSB planes does not scramble all bits,while the result is almost the same as that on all planes. The normal LSB-based bit-level image encryption method only performs independent bit scrambling in each bit plane.There is no bit position conversion between bit layers in the process of scrambling. Therefore,there is also more space for progress in the encryption effect obtained by the present chaotic image encryption methods based on bit permutation on LSB planes. To solve these problems,a novel LSB chaotic permutation based on FSV is proposed to exchange all necessary bit positions of the image. The proposed method changes the bit positions of the four different planes of the LSB of the image and reduces the information about the relation among the four LSB planes that contain the main information about the image. The proposed bit-level permutation can not only increase the range of pixel values changed by bit permutation,but also improve the ability to resist cryptanalysis with the application of chaotic systems. It is worth noting that the iteratively generated FSV will enhance the algorithm’s encryption performance to some degree.

The rest of this article is structured as follows. The basic principles and iterative algorithm of FSV,and chaotic LSB permutation based on FSV,are given in detail in Section 2. In Section 3, the FSV-LSBCP based image encryption and decryption algorithms are presented. In Section 4, the experimental results are discussed. Finally, some conclusions are drawn from the present study in Section 5.

2. Proposed methods

Inspired by Refs.[31–37],we introduce a new vector with fractal properties in order and analyze its characteristics in the application of image encryption in this section.

2.1. Basic concepts of FSV

Definition 1 A vectorV={v1,v2,...,vn} ∈R1×nis called a sorting vector if the elements in the vector are composed of positive integers 1,2,...,Nand the element values at any two different positions are different. In other words,Vis a sorting vector such that any of the following statements holds true:

Based on Definition 1, we define a class of vector with properties similar to the fractals as follows.

Definition 2 Sorting vectorV={v1,v2,...,vn}∈R1×nis called fractal sorting vector(FSV),if there are the following properties:

1) the distribution of elements in the vector is overall irregular;

2) the ordering of elements in each sub-vector with the same length is self-similar;

3) vectorVcan be generated by iteration.

2.2. Iterative algorithm of FSV

According to the definitions above, we give a class of fractal sorting vector construction method based on addition and multiplication between vector and number as follows.

Based on any initial vectorV[1]∈R1×l(V[1]), wherel(V)represents the length of the vectorV,we iterate it according to the following steps to obtain FSVV?.

Step 1 Calculate the iteration vectorV[2]according to the following iteration rules:

whereV{i}represents the i-th sub-vector ofV, andV(i) denotes the i-th element ofV.

Step 2 Repeat the following general term formulas to obtain the higher-order FSV,V[n].

Step 3 Obtain an FSVV?of any length from the following equation:

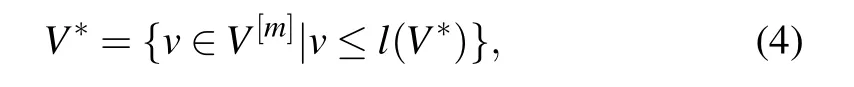
whereV[m]is a generated FSV calculated from steps 1 and 2,andl(V[m])≥l(V?).

Through the above steps, we can obtain the FSVV?of any length,by combining the actual needs and the appropriate number of iterations. The relationship between FSV and the initial iteration vector can be expressed as a function:

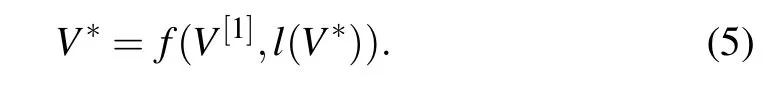
Based on these steps,we propose the pseudo-code to implement the iterative calculation of FSV as shown in Table 1.

Table 1. Pseudo-code of algorithm for FSV.

2.3. FSV based LSB chaotic permutation

The least significant bit of the image covers most of the information,[28]and the eight binary planes of peppers are shown in Fig. 1. The human eyes can clearly distinguish the information among the first four planes,but nothing from the last four. The information weight of the eight binary planes and their cumulative rates are shown in Table 2. The right four bits cumulatively contain 94.12%of the information. Processing the right four bits can be applied to the image encryption to improve the efficiency of the algorithm while ensuring security.

Fig.1. Eight binary planes of peppers: (a)8th,(b)7th,(c)6th,(d)5th,(e)4th,(f)3rd,(g)2nd,(h)1st.

Table 2. Information weights of bit planes.

Based on FSV and LSB permutation,a novel FSV-based LSB chaotic permutation method is proposed as follows.

Step 1 Represent each pixel in grayscale image into 8 bits. And use a tensorTSto represent the image represented by the bit.

Step 2 Denote the 8 layers of the tensor asP8,P7,P6,P5,P4,P3,P2,P1in sequence, whereP8is a binary image composed of the highest bit andP1is a binary image consisting of the lowest bit.

Step 3 Press the upper left, upper right, lower left, and lower right sub-block positions to composeP8,P7,P6,P5into a binary imagePLSB.

Step 4 Exchange the position of each bit inPLSBby the permutation vectors of the FSV and the ascending chaotic sequence index,successively.

Step 5 Split the new permuted binary imageP?LSBobtained in Step 4 intoP?8,P?7,P?6,P?5according to the sub-block positions in Step 3.

Step 6 RestoreP?8,P?7,P?6,P?5,P4,P3,P2,P1to a new grayscale image.

With the above six steps,the FSV-based LSB shaotic permutation of the image is realized. For better understanding,the flow chart is shown in Fig.2.

Fig.2. Process of FSV-based LSB chaotic permutation.

3. Image encryption algorithm based on FSVLSBCP

3.1. Two-dimensional chaotic system

In many chaotic systems,the Henon map has simple operations and can generate two chaotic sequences.And the Henon map is defined as[38]

wherea=1.4 andb=0.3 make the map reach a chaotic state.The application of the Henon map can make the image encryption method more difficult to predict and efficient to operate.

3.2. Encryption method

Image encryption method based on FSV-LSBCP is introduced in detail step by step in this subsection. Due to the flexibility of the proposed FSV construction algorithm, the proposed encryption algorithm,which is suitable to the images of any size and shape,mainly consists of six steps as follows.

Step 1 Read the plaintext image into the computer and mark it asP.

Step 2 Obtain an FSV of the appropriate length according to the proposed construction algorithm.

Step 3 Generate a 128-bit character stringΛby using SHA-512 fromP, and convertΛinto 3 decimalsK=[k1, k2, k3]as follows:

Step 4 Obtain the appropriate length chaotic sequencesC1andC2by Henon map with the parameters [k＇1, k＇2, k3],wherek3is the length of the deleted sequence to ensure chaotic state,whilek＇1andk＇2are the initial parameters of chaotic system. Setting private key[k4, k5],the parameters of the generated chaotic sequence are calculated as follows:

where mod(,)is the remainder function,and[k4, k5]is the private keystream.

Step 5 PermutatePintoP＇by FSV-LSBCP according to the FSV and the chaotic sequenceC1.

Step 6 Diffuse re-segmented imageP＇withC2by using the method shown below and denote the diffused image asP＇＇=[p＇＇(i)]:

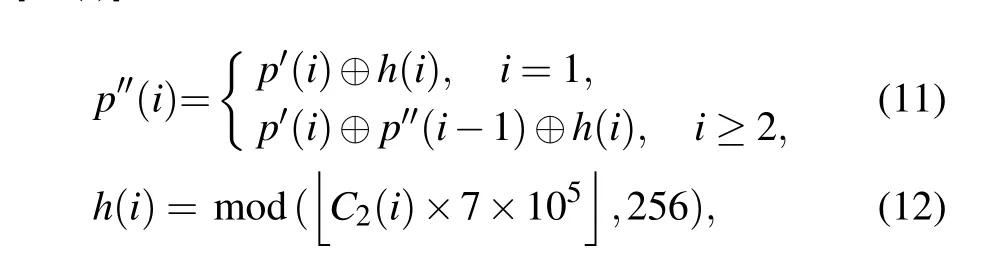
where⊕denotes XOR operation,andis the round-up function.

The ciphertext image is obtained by using the above six steps. The key sequence consists of [k1,k2,k3,k4,k5], which are used for both image encryption and decryption. For easy understanding,flow charts and examples of the above basis are shown in Figs.3 and 4,respectively.

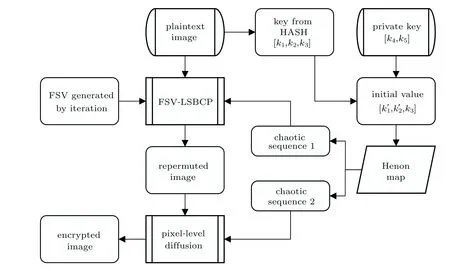
Fig.3. Flow chart of encryption algorithm based on FSV-LSBCP.

Remark 1 When the parameters of Eq. (6) are determined, different initial values can obtain different pseudorandom sequences after the same iteration. Thek＇1andk＇2calculated from Eq.(10)are used as the initial values of Eq.(6),that is,x0=k＇1andy0=k＇2. Then the pseudo-random sequences generated byk＇1andk＇2can be obtained. The lengths of these two sequences are determined by the size of the image. At the same time, to avoid the unsatisfactory pseudorandomness caused by the system in the front part of the sequence not entering the mixed state, the firstk3elements of each sequence are deleted andk3elements are iterated and converged at the end. The resulting pseudo-random sequences conform to the size of the image and can be well applied to encryption algorithms.

Remark 2 The hexadecimal sequence obtained by SHA-512,after the calculation of Eqs.(7)–(9)can obtaink1,k2,k3.These three keys are used as the keys generated by the plaintext image, which can make the encryption algorithm have good resistance to brute force attacks. The subjectively set keysk4andk5can effectively improve the ability of the encryption algorithm to resist the selected plaintext attacks. This key design method guarantees the comprehensive security of the algorithm. At the same time, the keys pass through a secure channel to avoid the possibility of the keys being stolen,thereby ensuring the security of ciphertext information in the key management.

3.3. Decryption algorithm

Using inverse transformation, the decryption and corresponding experimental test can be completed by using the key sequence provided in the encryption algorithm.

Step 1 Read the encrypted image into the computer. Call the image matrixPE=[pe(i)].

Step 2. Obtain an FSV of the appropriate length according to the proposed construction algorithm.

Step 3. Obtain the chaotic sequencesC1andC2by using the previously described system and processing method with the group key[k1,k2,k3,k4,k5].

Step 4. Back-diffuse re-segmented matrixPEwithC2through using the method shown below and denote the backdiffused image matrix asP＇E=[p＇e(i)]:

Step 5 PermutateP＇EintoP＇＇Eby reverse process of FSVLSBCP.

This concludes the decryption process, which is the reverse of the encryption process. The demonstration is no longer illustrated as space limitations.

3.4. Encryption and decryption simulation results

Fig. 4. Image encryption/decryption results, showing (a) image of Fullgold, (b) encrypted Fullgold, (c) decrypted Fullgold, (d) image of Lena, (e)encrypted Lena,(f)decrypted Lena,(g)image of peppers,(h)encrypted peppers,(i)decrypted peppers.

MATLAB 2017a software is used to conduct the encryption and decryption in this study. The operation system of the computer is a Microsoft Windows 10 system with Intel(R)Core(TM)i5-7500 CPU.The encryption and decryption simulation results of three representative images,each with a size of 512×512, are shown in Fig. 4. The simulation results illustrate the accurate process of encryption and decryption in terms of visual effect.

3.5. Encryption runtime comparison

LSB chaotic permutation reduces the operation of bit position transformation. This design can effectively reduce the running time of the proposed encryption algorithm, and its comparisons with the running times of some classic algorithms are shown in Table 3. Through the comparisons, it can be found that the proposed encryption method can effectively improve the efficiency of image encryption.

Table 3. Comparisons among runtimes.

4. Security analysis

Numbers of experimental results and data comparisons are provided in this section to check the supremacy and protection of proposed image encryption and decryption algorithms based on FSV-LSBCP.The images,each with a size of 512×512 used for the experimental test,are shown in Fig.5.

Fig.5. Images used for experimental test on(a)baboon,(b)Barbara,(c)bridge,(d)couple,(e)crowd,(f)Fullgold,(g)Lena,(h)man,(i)peppers,(j)plane.

4.1. Key analysis

According to the conclusion in Ref. [39], the cryptosystem with keyspace larger than 2100is better at resisting bruteforce attacks. Due to the calculation accuracy and the selected space of the initial matrix, the keyspace can be calculated as follows:

where the selection space ofk1,k2,k4,k5is 1014as the calculation accuracy of the computer is assumed to be 10?14,the selection space ofk3is 103.

The key sensitivity test can detect the effect of small changes of the correct key on the decryption of ciphertext.Any accurate image cannot be decrypted unless the right keyKr=[k1, k2, k3, k4, k5] is used in the proposed cryptosystem. The error keysK1= [k1+10?14, k2, k3, k4, k5] andK2=[k1, k2+10?14, k3, k4, k5]are used to decrypt the ciphertext,respectively. There is no doubt that the wrong key cannot obtain the correct decrypted image, and even if the two images are subtracted, no relevant information can be obtained.The detailed simulation process of key sensitivity analysis is shown in Fig.6.

4.2. Statistical analysis

Kinds of statistical experiments and analysis are enumerated to verify the reliability of the proposed algorithm as follows.

4.2.1. Histogram analysis

The ciphertext image histogram is a method used to calculate the ability of an encryption system to object to a statistical analysis attack.This suggests that it is difficult to attack the ciphertext image obtained by the encryption algorithm when the histogram is smooth.As shown in Fig.7,the histograms of the encrypted and decrypted images have obvious characteristics,where the histograms of the original images have various fluctuations but the histograms of these ciphertext images are very stable.

Fig.6. Key sensitivity test on(a)encrypted peppers with Kr,(b)decrypted peppers with Kr,(c)decrypted peppers with K1,(d)decrypted peppers with K2,(e)absolute value of(c)minus(d),and(f)histogram of panel(e).

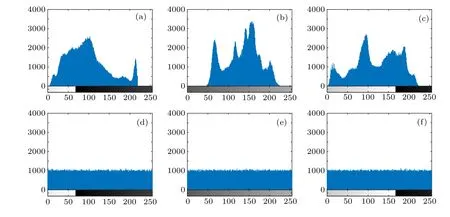
Fig.7. Histograms of(a)Fullgold,(b)Lena,(c)peppers,(d)encrypted Fullgold,(e)encrypted Lena,and(f)encrypted peppers.

4.2.2. Correlation coefficient

The correlation coefficient is a description of the correlation between two adjacent pixels. For a flat image,its adjacent pixel relationship is divided into three categories: horizontal,vertical,and diagonal.The correlation coefficients of the three directions of the ciphertext image obtained by a secure image encryption algorithm should be small enough to resist attacks.The correlation coefficients of the flat image are calculated as follows:[40]

where

Table 4 shows the comparisons of correlation coefficients between the ciphertext images and the original images. The correlation coefficients of the representative encrypted images are generally very small. The mean values in the horizontal,vertical,and diagonal directions of the correlation coefficients are?0.000271,?0.000358, and 0.000654, respectively. The small standard deviations in the three directions indicate that the proposed method is safe and stable.

The visual correlation results of the image peppers before encryption and after encryption are shown in Fig.8.The correlations in the three directions of the two original images are all concentrated around the liney=xof the coordinate system,while most of the points are close to the line, which means that the original images are relevant to each other. In contrast to the correlation image of the ciphertext image,each point is evenly distributed in the image range, which reveals that the correlation of the encrypted image is weak.

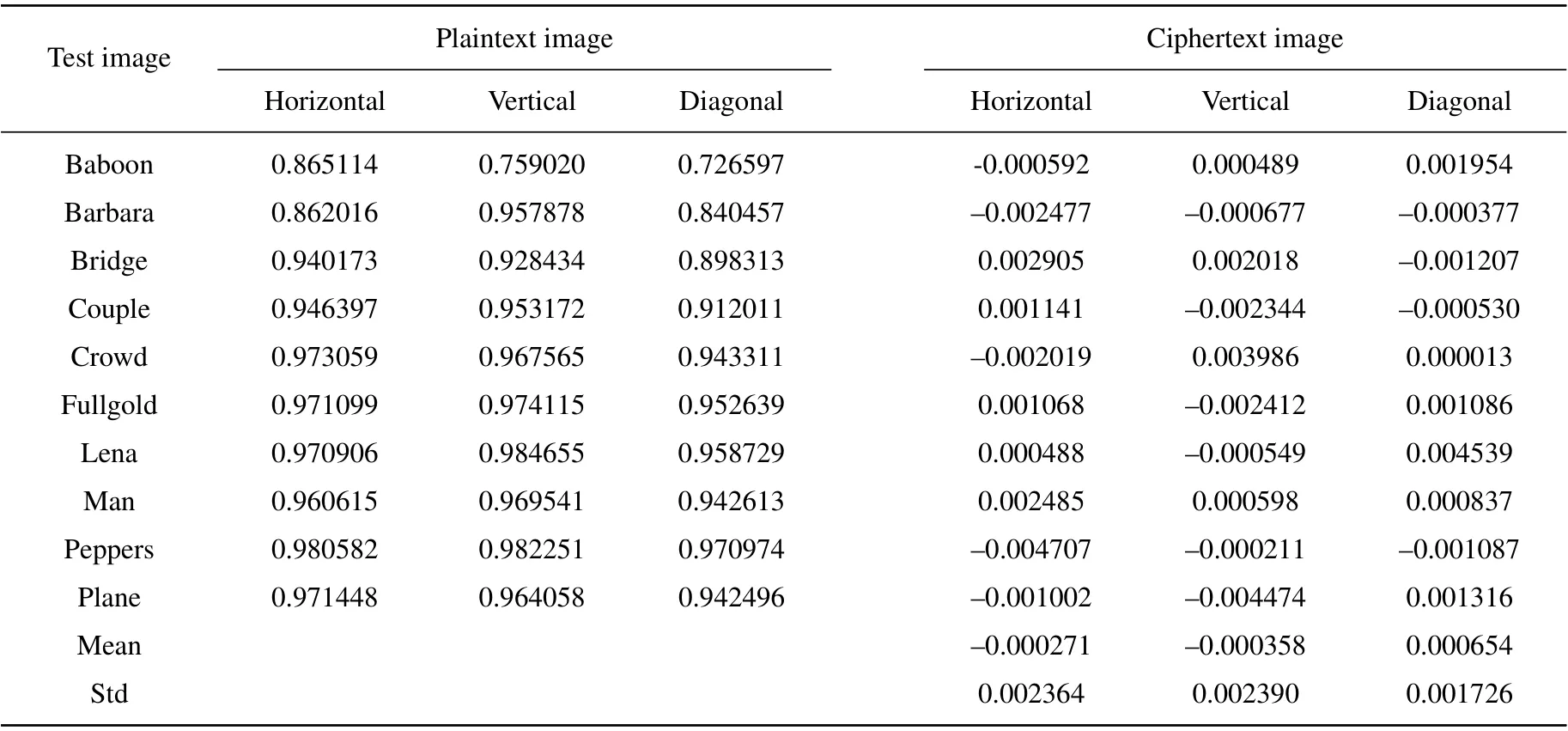
Table 4. Correlation coefficients of images before and after being encrypted.

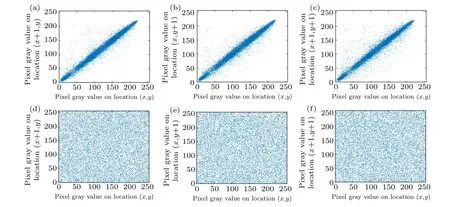
Fig.8. Adjacent pixel correlation in(a)horizontal direction of peppers,(b)vertical direction of peppers,(c)diagonal direction of peppers,(d)horizontal direction of encrypted peppers,(e)vertical direction of encrypted peppers,and(f)diagonal direction of encrypted peppers.

4.2.3. Information entropy

An important parameter that represents the randomness of information is information entropy,which is expressed as[41]

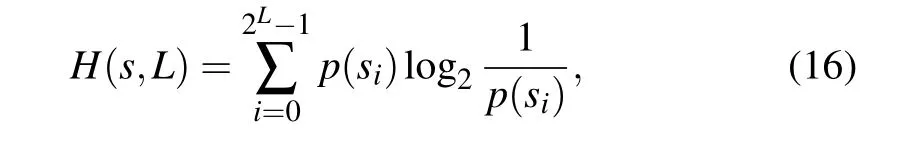
where descriptions of parameters such ass=[si]2L,p(si),andsiare detailed in Ref.[41].

Table 5 accurately reflects the change in information entropy of the image before and after encryption, that the information entropy after encryption is closer to the theoretical limit value. The standard deviation is 0.000060, which is small,implying that the proposed algorithm is both safe and stable.

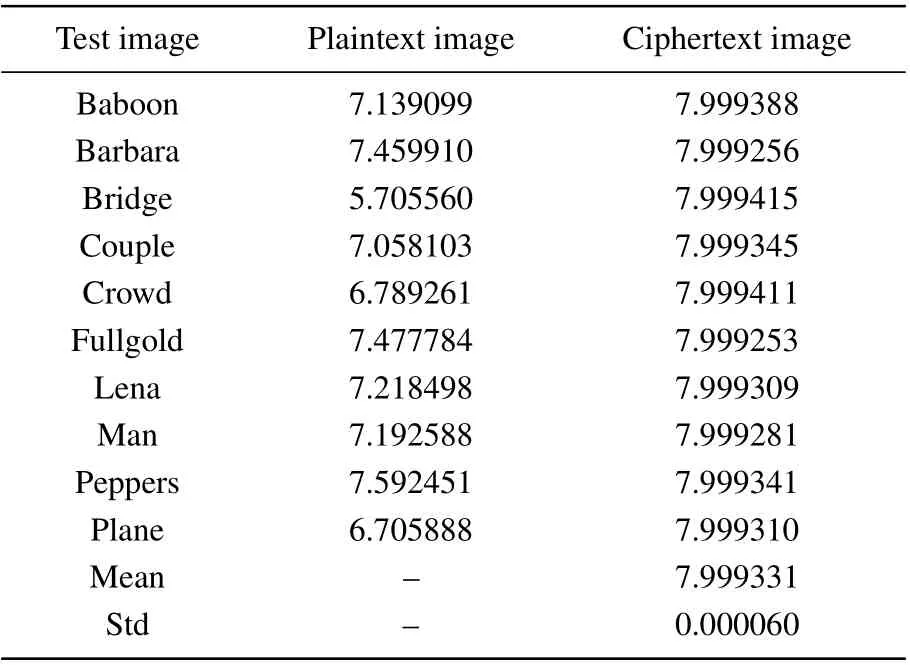
Table 5. Information entropy of plaintext and ciphertext images.

4.3. Analysis of resistance to differential attack

The resistance of encryption algorithms to differential attacks can be tested by the number of pixels changing rate (NPCR) and unified averaged changed intensity (UACI),which are acquired as follows:[17]

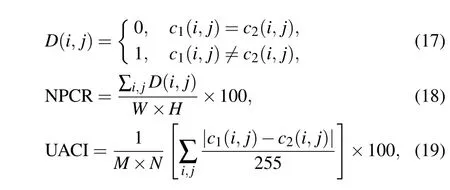
wherec1(i,j)andc2(i,j)are two pixel values of the same position (i,j) in the two different encrypted images;MandNrepresent the image dimensions.

Table 6 shows the average values of the NPCR and UACI among 100 random pixels at different positions. Selecting the mean value of NPCR and UACI at random positions can avoid the particularity of special positions in the calculation process and the waste of time in obtaining the overall value.The NPCR and UACI values of each image and their average values are close to the theoretical level 99.6094% and 33.4635%, respectively. Although the standard deviation of UACI is slightly larger than that of NPCR, they are not very large. This makes our algorithm stable while being safe, and the proposed method is suitable for various types of images.In general,the proposed method has a high resistance to the differential attack. Therefore,the proposed encryption scheme is verified to resist differential attacks.

Table 6. NPCR and UACI values of ciphertext images(%).

4.4. Resistance to cropping attacks and noise attacks

The cropping attacks and noise attacks are used to disrupt the integrity of the ciphertext image, which will prevent the attacker from obtaining the correct decryption information. In the resisting cropping attacks experiment, the encrypted images at the degrees of 1/16 and 1/4 cropping are decrypted as shown in Fig.9.

Fig. 9. Decryption results after cropping attacks, showing (a) encrypted peppers with 1/16 degree cropping, (b) decrypted image of panel (a), (c)encrypted peppers with 1/4 degree cropping,and(d)decrypted image of panel(c).

Fig.10. Decryption results after salt pepper noise attacks,showing(a)decrypted Lena after 1%noise,(b)decrypted Lena after 5%noise,(c)decrypted Lena after 10%noise,and(d)decrypted Lena after 25%noise.

Table 7. Comparisons of proposed method with other bit-level permutation encryption methods.

In the experiment on resisting salt and pepper noise attacks,the encrypted images with noise strengths of 0.01,0.05,0.10, and 0.25 are decrypted as shown in Fig. 10. The proposed cryptosystem can effectively resist cropping attacks and noise attacks and can decrypt identifiable plaintext images from ciphertext images that have been damaged to varying degrees.

4.5. Comparison with other algorithms

In the previous part, the experimental results of several indicators were introduced,and finally,the average values are used to compare with the experimental indicators, and thus comparing the proposed algorithm with other methods. The comparisons of performance between the proposed encryption scheme and other pixel-level permutation image cryptosystems are list in Table 7.

The proposed algorithm presents good comprehensive experimental performance,showing that the proposed cryptosystem is both safe and reliable.

5. Conclusions

A chaotic image encryption cryptosystem based on FSVLSBCP is proposed for achieving the image with any size in this work. The basic concepts and iterative algorithm of FSV are introduced in detail. The fast iterative FSV can effectively improve the efficiency of encryption algorithms. The bit permutation of LSB can not only ensure the encryption effect but also improve the encryption efficiency. Combined with the dynamic characteristics of FSV, a new FSV-LSBCP is presented. The chaotic image encryption and decryption algorithm based on the FSV-LSBCP is constructed to encrypt and generate ciphertext images with stronger resistance to attacks. Through the comparison of encryption time, statistical analysis, and analysis of resistance to differential attacks, the proposed method proves to have a large enough keyspace,sufficiently sensitive key, and unrivaled resistance to statistical attacks and differential attacks.