帶壓縮性修正的離散渦方法在結冰數值模擬中的應用

周澤堃，周峰，王剛

（1.西北工業大學 航空學院，西安710072）

（2.中國商用飛機有限責任公司上海飛機設計研究院，上海201210）

0 引 言

飛行器結冰是危害飛行安全的嚴重問題之一，輕則影響飛行器的飛行性能，重則造成機毀人亡的慘重后果［1-2］。而對飛機進行結冰數值模擬則成為一種研究飛行器結冰問題的有效途徑。國際上商用的結冰數值模擬軟件包括美國NASA的Lewice［3］和加拿大的FENSAP-ICE［4］等。

在結冰數值模擬研究中，國內起步較晚，目前也做了很多深入研究，易賢等［5］采用歐拉法計算了三維復雜外形表面的水滴收集率；周峰等［6］對部分典型二維翼型進行了結冰數值模擬；Xie L等［7］提出一種自適應插值方法將拉格朗日法計算得到的水滴收集率插值到三維復雜外形上；桑為民等［8］在進行大粒徑水滴狀態下的結冰模擬時考慮了水滴變形破碎的影響；杜雁霞等［9］對結冰過程涉及的熱力學行為的研究現狀進行了總結和展望；王海濤等［10］對機翼進行結冰數值模擬并設計了一套防除冰系統。

飛行器結冰數值模擬主要包括網格生成、計算流場、水滴撞擊特性計算、結冰模型計算和結冰冰形生長計算五個模塊。在流場計算時，通常采用經典的有限體積法求解N-S方程。相比于經典CFD方法，離散渦方法［11］可以不考慮網格，數值耗散低，適用于結冰這類易產生分離流動問題的分析。國內外研究者對離散渦方法進行了應用和發展。國外，K.Ramesh等［12］運用離散渦方法模擬翼型前緣產生的間歇渦運動；E.G.A.Antonini等［13］提出一種改進的離散渦方法來模擬二維翼型俯仰中的動態失速現象。國內，馬明憲等［14］使用離散渦方法計算了湍流混合層的問題；董婧等［15］運用離散渦方法模擬了圓柱繞流問題；吳文權等［16］采用拉格朗日粒子法對脹量項計算，從而實現離散渦方法在可壓縮流動下的計算；劉佳等［17］將離散渦方法應用于計算結冰數值模擬，與經典CFD下的結冰數值模擬過程相比，在保證精度的同時，計算效率得到提升。但是離散渦方法主要針對不可壓流動求解，對于可壓縮流動下的冰形模擬的應用仍有所欠缺。

本文在基于離散渦方法結冰模擬的基礎上，引入普朗特—格勞爾特壓縮性修正，將該方法的計算結果拓展到可壓縮區間，結合改進的Messinger熱力學模型［18］實現可壓縮狀態下翼型的結冰模擬。通過部分二維翼型的結冰數值模擬，將模擬結果與基于有限體積法的經典CFD方法下模擬結果及實驗值進行對比，并分析引入壓縮性修正前后對流場、結冰過程和結冰冰形的影響。

1 結冰數值模擬方法

1.1 離散渦方法基本原理及改進

二維不可壓N-S方程的控制方程［19］可表示為

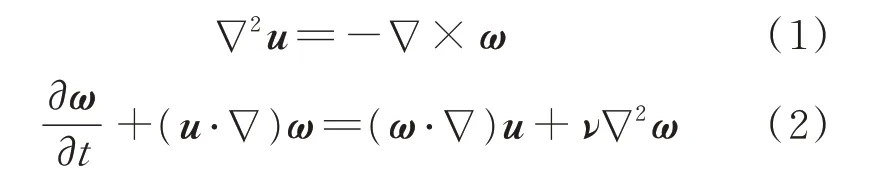
式中：ν為動力黏度；u為速度矢量；ω為渦量。

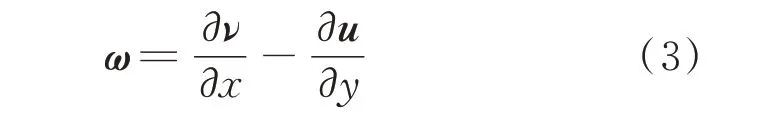
離散渦方法是將流場渦量離散化，在拉格朗日框架下模擬流場渦量。通過采用算子分裂法，式（2）可以分成兩部分，即對流項式（4）與擴散項式（5）。

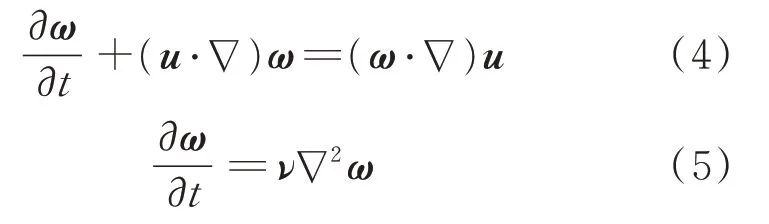
在二維不可壓無黏條件下，得到：

流體微團在運動過程中渦量始終不發生改變，并且不隨流體質點遷移運動。

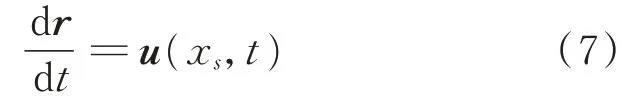
式中：r為渦元距離原點的位移矢量；x s為渦元所處位置的坐標。

為了避免點渦在距離其無窮近處出現誘導速度無窮大的奇性問題，通過A.J.Chorin［20］提出的渦團法，渦量分布方程可變為

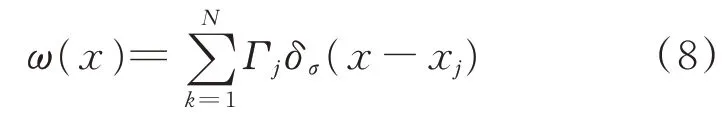
式中：N為渦團數；Γj為渦團的環量；δσ(x-x j)為渦量的分布函數。

在得到渦量分布后，依據Biot-Savart定律［21］得到速度場：

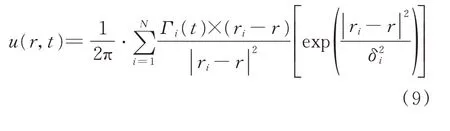
計算得到流場的速度分布后，就可以獲得渦元的運動軌跡，再計算出下一時刻的渦量場。通過隨機走步法［22］來模擬渦元的擴散運動，即：

式中：μ為滿足高斯分布的隨機數，其均值為零，方差為

在大多數工程問題中，必須滿足特定的邊界條件，流場才能求解。根據亥姆霍茲（Helmholtz）定理，得出在均勻流中不會產生渦量，只有在物體邊界或者流場受非保守力作用時才會有渦量產生。本文通過壁面無穿透邊界條件確定流場中生成的渦量。整個流場在滿足Kelvin環量定理的前提下，通過速度場與渦量場之間交替迭代計算，就能模擬出Lagrangian框架下的繞流流動。

上述是離散渦方法的基本原理，在基本原理的基礎上本文對離散渦方法進行一些改進，包括渦元合并、控制區高度修訂及壓力計算［23］等，具體參見文獻［17］。

1.2 二維結冰熱力學模型

基于改進的Messinger熱力學模型［18］，將結冰表面分為若干控制體，每個控制體的質量流動情況如圖1所示。在一些假設條件下，該模型通過求解質量和能量守恒方程［24］最終求解出結冰質量。

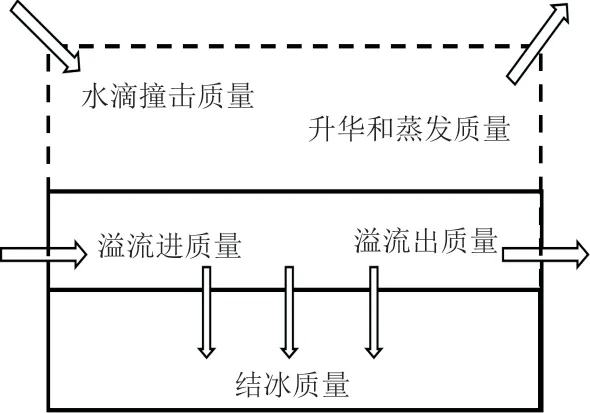
圖1 控制體內質量流量示意圖Fig.1 Sketch of mass variation in control volume

建立質量守恒方程（11）和能量守恒方程（12），定義每個控制體內的凍結系數f如式（13）所示。

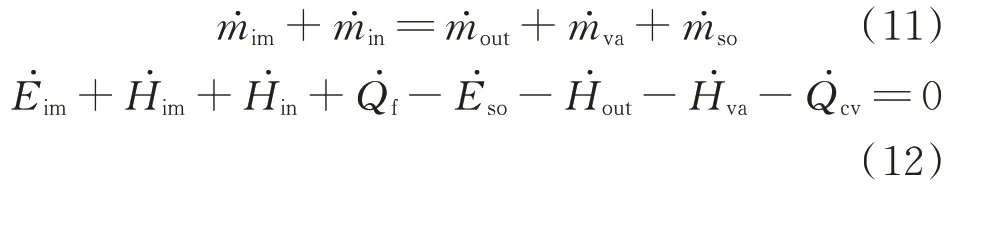
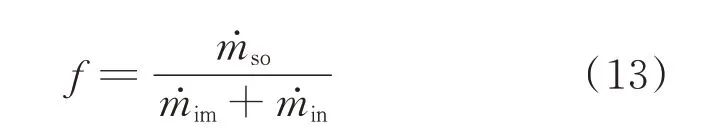
式中：為控制體內的水滴撞擊質量；為液態水溢流進入控制體的質量為液態水溢流出控制體的質量；為升華和蒸發質量；為結冰質量；為控制體內水滴撞擊的動能；為控制體內水滴撞擊的焓變；為液態水溢流進控制體的焓變為氣動摩擦熱；為結冰所釋放的潛熱；為液態水溢流出控制體的焓變；為液態水蒸發潛熱；為對流換熱熱能。

聯立式（11）、式（13），通過提取表面溫度作為試探參數，對方程組求解，從而確定壁面各控制體內的壁溫、凍結系數和各個質量項。在得到結冰表面各控制體內的每個質量項后，就可以依據結冰增長模型，計算出單次時間步長內冰層的厚度。

1.3 普朗特—格勞爾特壓縮性修正

離散渦方法適用于不可壓流動，在當下的研究進展中，已經實現可壓縮流動下的離散渦方法。但是引入壓縮性修正，將離散渦方法的結果擴展到可壓縮區間仍是一種簡易的方法。

對二維翼型壁面附近的繞流速度采用小擾動假設，如圖2所示。

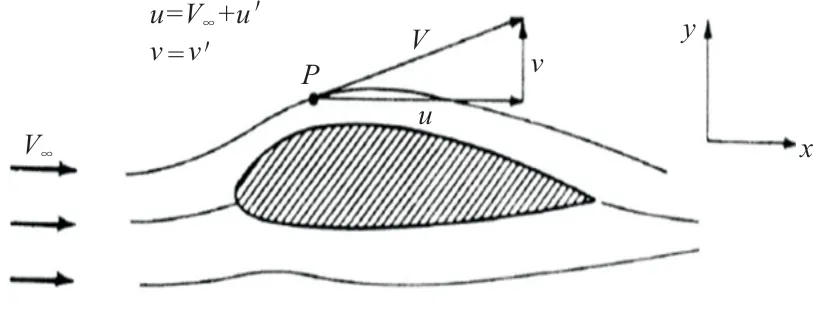
圖2 二維翼型繞流［25］Fig.2 Flow around two-dimensional airfoil［25］

假設流動的總焓不發生改變，構建式（14）：

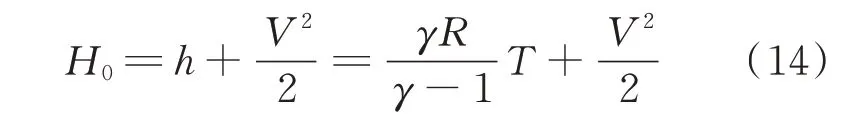
式中：H0為流動的總焓；h為當地流體的焓值。

在式（14）中，給定遠場的靜溫，求解建立溫度場，結合理想氣體假設下的狀態方程對壓力場修正，并計算出當地密度：

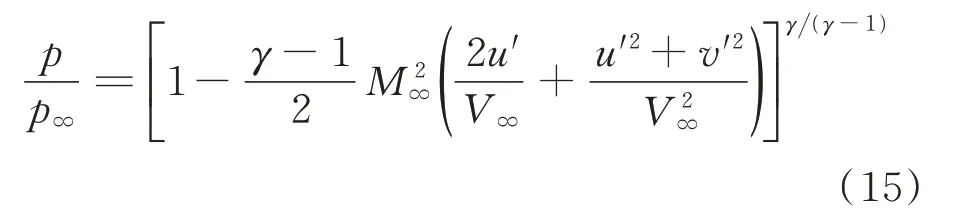
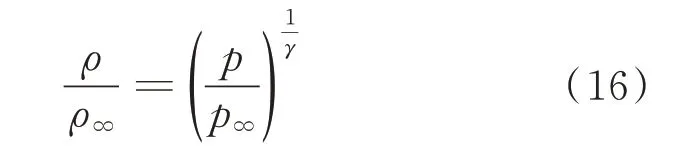
壁面參數采用式（17）進行修正：

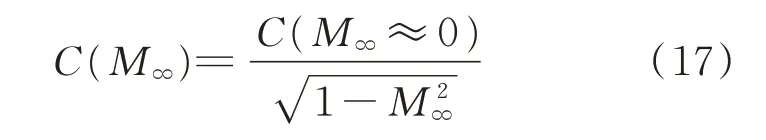
通過式（15）～式（17）對采用離散渦方法計算得到的壓力、密度和壓力系數進行一次修正。

對二維不可壓N-S方程的動量守恒式進行簡化得到：

式（18）等價于：

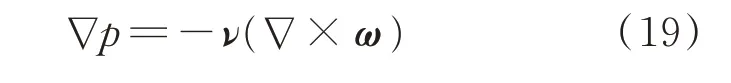
在壁面處通過渦量對壁面壓力進行計算，而在壁面處u=0，式（2）簡化為

渦量流量為-ν?ω，通過邊界的流量為，即壁面渦量的生成比率。

壁面的法向和切向用s和n表示，在二維表面得到：

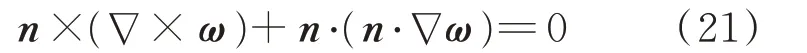
由式（19）～式（21）得到：

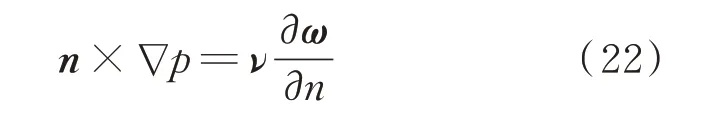
即：

因為在每個時間步均有新渦生成，所以上述環量生成率是已知的。根據梯形法則，由式（23）得到：

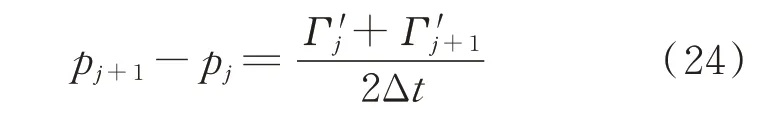
式中：pj+1和p j為沿壁面單元節點上的壓強；和為在一個時間步長Δt下的新生渦環量。

通過式（15）對壁面壓強進行修正，利用式（24）中修正的壁面壓強對渦團環量進行修正，將修正后的渦團環量分別代入式（8）和式（9），求解壁面渦量和速度場，最后通過式（14）～式（17）對壓強、密度和壓力系數再次修正。

2 算例驗證與分析

2.1 離散渦結冰模擬結果及驗證分析

基于離散渦方法進行不可壓流動下的結冰數值模擬，以NLF-0414翼型和Business Jet機翼翼型作為算例并與實驗值［26］進行對比，以驗證本文中未采用壓縮性修正下算法和程序的正確性。主程序是將翼型表面分成220塊主板塊，每塊主板塊分成5個次板塊。由于前緣易發生流動分離，壁面離散單元在前緣加密。計算流程如圖3所示，單次結冰模擬時長為60 s，若未滿足最終結冰模擬時長則再循環計算。

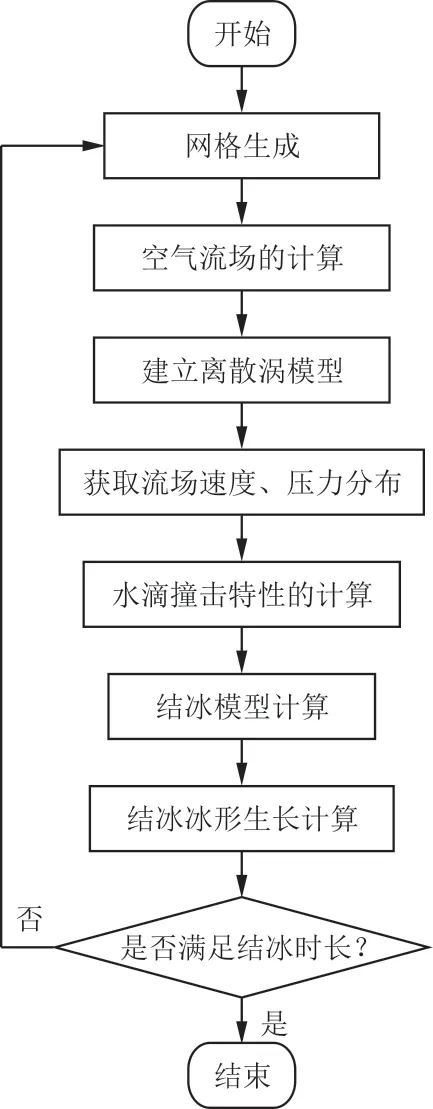
圖3 結冰數值模擬計算流程Fig.3 Workflow of icing numerical simulation

NLF-0414翼型計算條件如下：來流速度66.9 m/s，攻角0.3°，弦長0.9 m，靜壓93 182 Pa，水滴直徑20μm，液態水含量0.44 g/m3，來流靜溫-15.0℃（霜冰狀態），結冰總時長240 s。該工況下結冰模擬結果與實驗值［26］的對比如圖4所示。

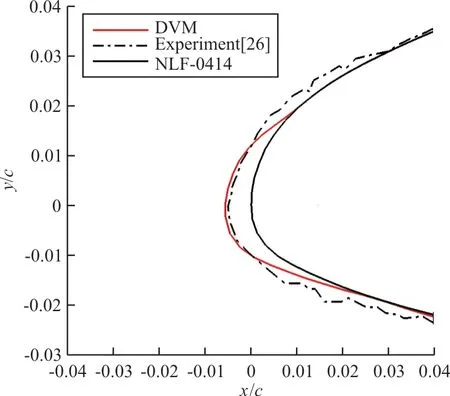
圖4 NLF-0414翼型結冰冰形比較Fig.4 Comparison of ice shape for NLF-0414 airfoil

Business Jet機翼翼型計算條件如下：來流速度90 m/s，攻角6.1°，弦長0.9 m，靜壓94 562 Pa，水滴直徑20μm，液態水含量0.54 g/m3，來流靜溫-5.0℃（明冰狀態），結冰總時長360 s。該工況下結冰模擬結果及與實驗值［26］的對比如圖5所示。

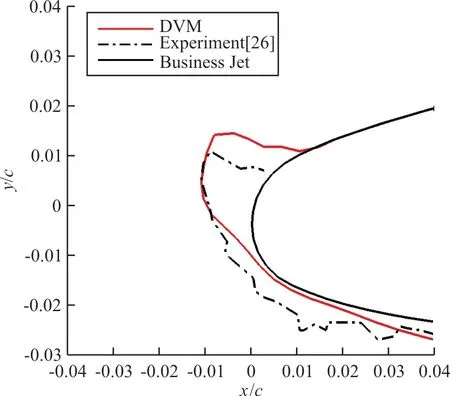
圖5 Business Jet機翼翼型結冰冰形比較Fig.5 Comparison of ice shape for Business Jet wing airfoil

在未考慮壓縮性修正的情況下，基于離散渦方法的結冰模擬結果與實驗結果輪廓貼近，說明采取的方法在不可壓流動下可以較好地模擬翼型結冰過程，從而證明了本文求解流程和計算程序的正確性。然而，當前方法未考慮流動的壓縮性，可以在此基礎上進行壓縮性修正，以提高程序在可壓縮流動下的預測能力。

2.2 引入修正后離散渦結冰模擬結果及驗證分析

選取NACA 0012翼型和Business Jet機翼翼型進行計算驗證。在選取相同結冰模型的情況下，分別采用未考慮壓縮性修正的離散渦方法（DVM without correction）、引入壓縮性修正的離散渦方法（DVM with correction）以及經典CFD方法（Classical CFD）計算流場并最終得到結冰冰形。

算例1：NACA 0012翼型，來流速度129 m/s，攻 角4°，弦 長0.3 m，靜 壓90 750 Pa，水 滴 直 徑20μm，液態水含量0.5 g/m3，來流靜溫-12.6℃，結冰總時長120 s。

計算結果與文獻［27］中的Lewice軟件模擬結果和實驗值進行比對，如圖6所示，可以看出：基于離散渦方法引入修正前后結冰模擬結果上冰角接近，下冰角處有差異，考慮壓縮性修正的離散渦方法最終冰形的下冰角處與經典CFD方法結果、文獻結果均符合的較好。

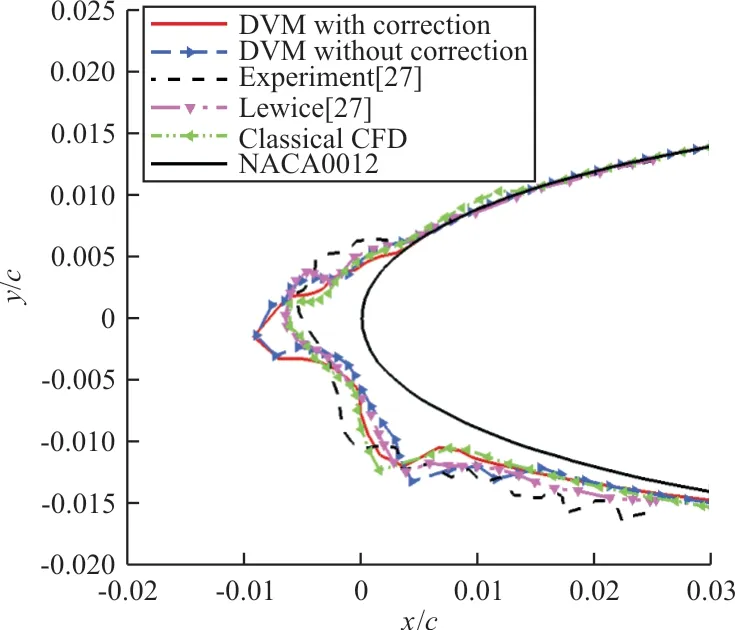
圖6 算例1結冰冰形比較Fig.6 Comparison of ice shape for Case 1

通過單次結冰模擬結果分析離散渦方法引入壓縮性修正對流場和結冰的影響，該算例第60 s結冰模擬結果如圖7所示。

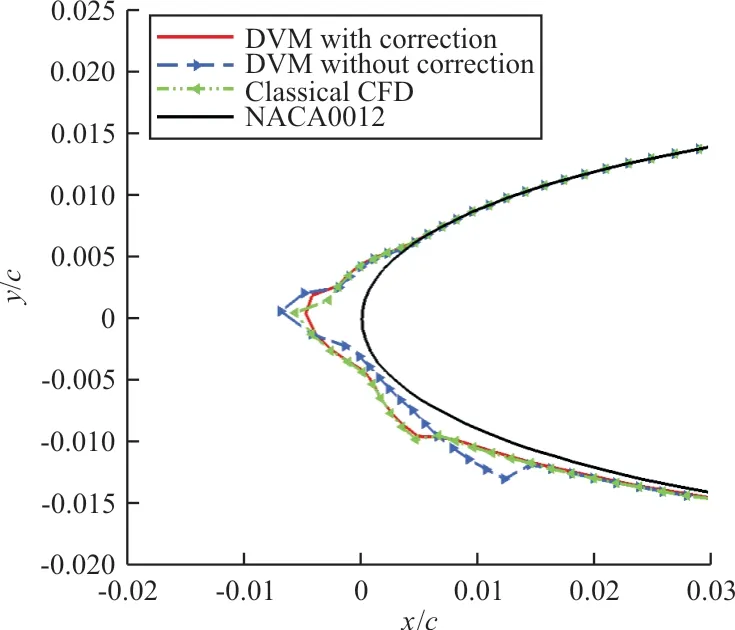
圖7 算例1第60 s結冰冰形比較Fig.7 Comparison of ice shape for Case 1 in 60 s

從圖7可以看出：第60 s未考慮壓縮性修正的離散渦方法與經典CFD方法的最終冰形輪廓不一致。相比未考慮壓縮性修正的離散渦方法，引入修正后方法與經典CFD方法的最終冰形更符合。

在計算第60 s冰形時需要初始干凈翼型的流場數據。計算算例1的干凈翼型時，流場壓力系數對比如圖8所示，流場馬赫數對比如圖9所示，可以看出：修正后離散渦方法與經典CFD方法計算得到的壓力系數和馬赫數更加接近，修正后離散渦方法可以較好地模擬流場。

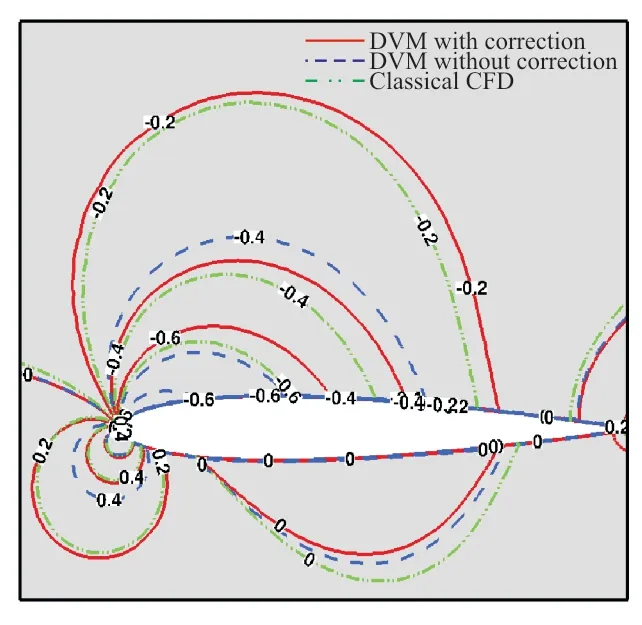
圖8 算例1流場壓力系數對比Fig.8 Comparison of pressure coefficient in flow field for Case 1

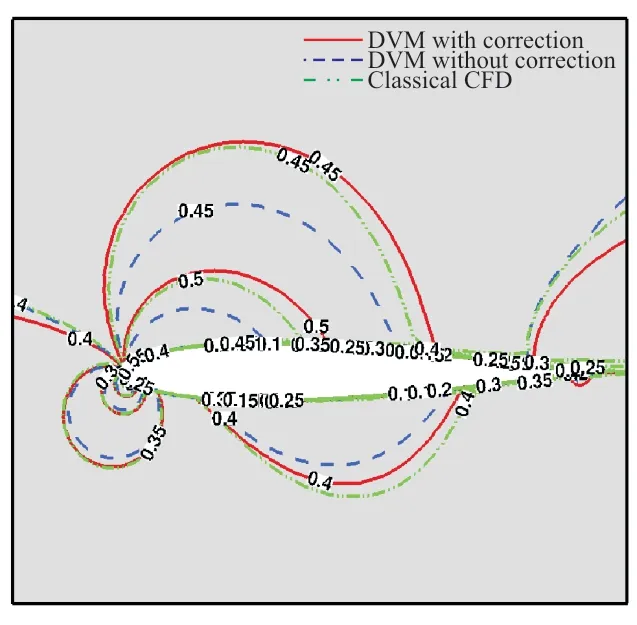
圖9 算例1流場馬赫數對比Fig.9 Comparison of Mach number in flow field for Case 1

分析離散渦方法引入修正前后對結冰模型計算過程的影響，算例1第60 s通過結冰模型得到的表面水含量如圖10所示，橫坐標為沿駐點兩側翼型弧長s與弦長c比值的無量綱距離，0為駐點位置；縱坐標表面水含量表示單位表面積上撞擊和溢流入當前單元的質量流量與流出蒸發的質量流量的差值。

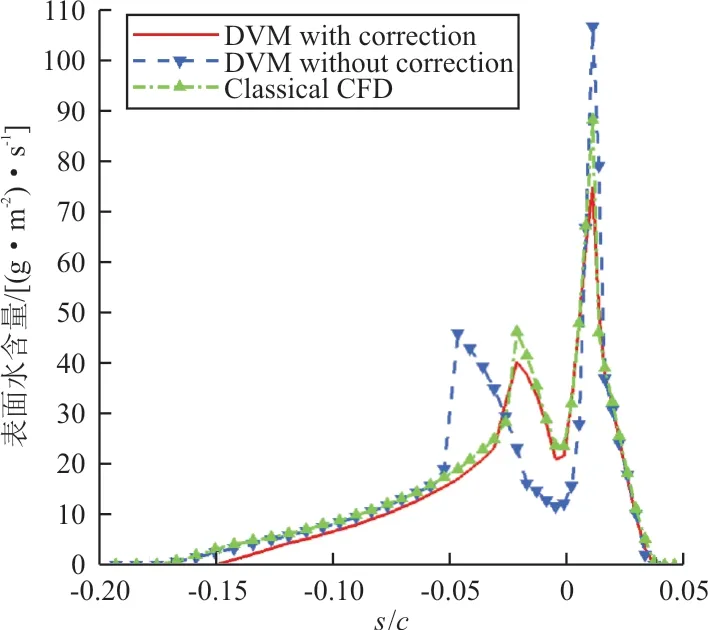
圖10 算例1第60 s表面水含量對比Fig.10 Comparison of water quality on surface for Case 1 in 60 s

算例1第60 s通過結冰模型計算得到的凍結系數如圖11所示。

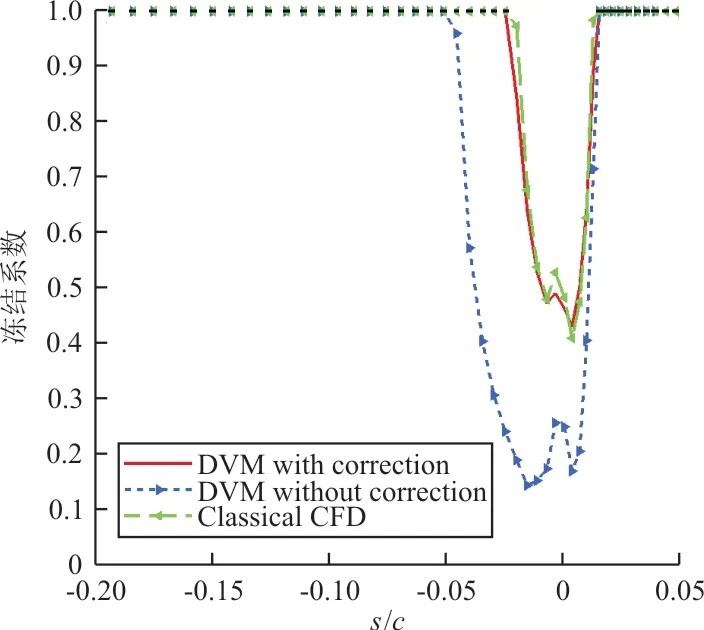
圖11 算例1第60 s表面凍結系數對比Fig.11 Comparison of freezing factor on surface for Case 1 in 60 s

從圖10～圖11可以看出：引入壓縮性修正后經結冰模型得到的表面水含量和凍結系數與經典CFD方法經結冰模型得到的結果更為接近，說明引入修正后的離散渦方法相比未考慮修正的方法模擬結冰過程更準確。

算例2：Business Jet機翼翼型，來流速度129 m/s，攻角1.5°，弦長0.9 m，靜壓89 040 Pa，水滴直徑20μm，液態水含量0.31 g/m3，來流靜溫-5℃，結冰總時長360 s。

計算結果與文獻［26］中實驗結果對比如圖12所示，可以看出：未考慮修正的離散渦方法最終模擬冰形與實驗值相比，最終冰形輪廓相差過大，而引入修正后最終模擬冰形與實驗值貼近。

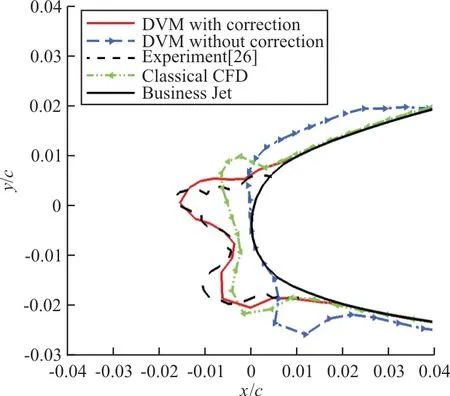
圖12 算例2結冰冰形比較Fig.12 Comparison of ice shape for Case 2

算例2第60 s結冰模擬結果如圖13所示，可以看出：引入修正后最終模擬冰形與經典CFD方法的結果更符合。

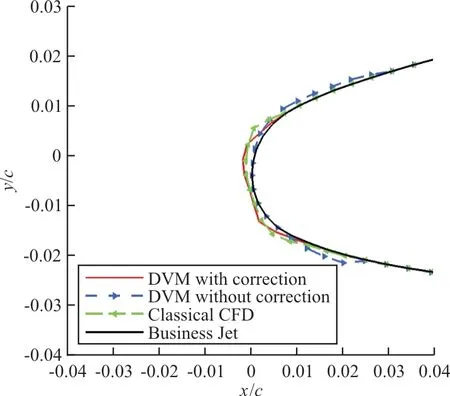
圖13 算例2第60 s結冰冰形比較Fig.13 Comparison of ice shape for Case 2 in 60 s

計算算例2采用干凈翼型時，流場壓力系數對比如圖14所示。

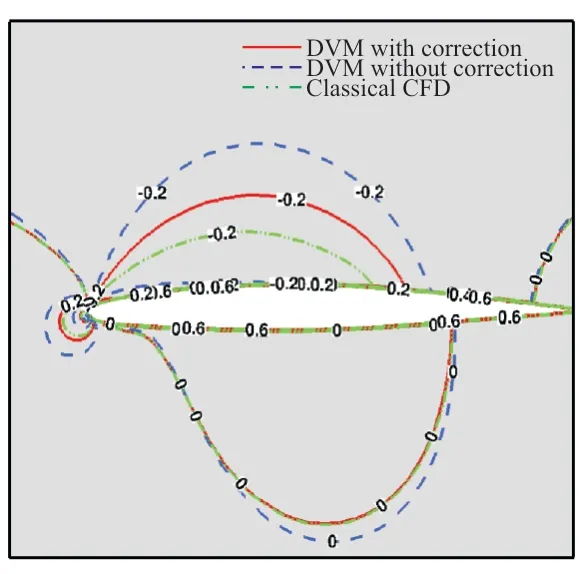
圖14 算例2流場壓力系數對比Fig.14 Comparison of pressure coefficient in flow field for Case 2

從圖14可以看出：相較修正前離散渦方法計算結果，修正后計算得到的壓力系數與經典CFD方法結果更加接近。

將算例2第60 s通過結冰模型得到的表面水含量和凍結系數進行對比，如圖15～圖16所示，可以看出：引入修正后經結冰模型得到的表面水含量和凍結系數與經典CFD方法經結冰模型得到結果更為接近；未考慮修正時經結冰模型計算出的表面水量在駐點附近基本沒有，此時駐點附近無流入水量，而撞擊到壁面的水量全部流入附近的單元內，最終凍結系數在駐點附近接近為0。引起這一問題的主要原因是未考慮壓縮性的離散渦方法在結冰模型中壁面單元附近的壁溫與引入修正后結果有明顯差異，未修正方法計算駐點附近的壁溫大于0℃，液態水無法凍結而流向其他單元。而引入修正后方法與經典CFD方法在結冰模型中的駐點附近壁溫小于或等于0，使液態水在駐點附近結冰。

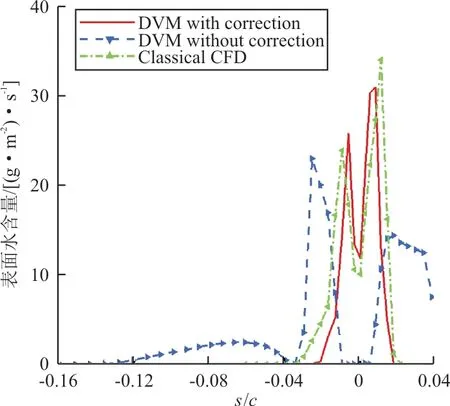
圖15 算例2第60 s表面水含量對比Fig.15 Comparison of water quality on surface for Case 2 in 60 s

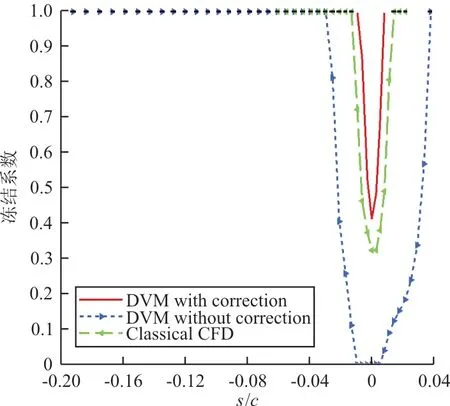
圖16 算例2第60 s表面凍結系數對比Fig.16 Comparison of freezing factor on surface for Case 2 in 60 s

3 結 論

（1）相比未考慮修正前的方法，引入壓縮性修正后的離散渦方法可以較好地模擬可壓縮流動狀態下的翼型的流場，最終模擬冰形與實驗值和經典CFD方法結果更為接近。

（2）在可壓縮流動下的結冰數值計算中，引入修正的離散渦方法對結冰過程中的凍結系數和表面水含量的計算結果改進明顯，與經典CFD計算方法結果符合較好。