具有恐懼效應(yīng)和Allee效應(yīng)的合作捕食系統(tǒng)的穩(wěn)定性分析

葉鵬輝

（安慶師范大學數(shù)理學院，安徽安慶 246133）

捕食者-食餌模型一直是生物數(shù)學研究的重要問題。近幾年關(guān)于捕食者對食餌產(chǎn)生的恐懼效應(yīng)吸引了眾多學者的關(guān)注，有學者研究了一系列關(guān)于功能反應(yīng)函數(shù)的恐懼效應(yīng)[1-2]，也有學者研究了在一般的線性功能反應(yīng)下捕食者不僅會對食餌產(chǎn)生恐懼效應(yīng)，還會由捕食者的捕食行為對食餌產(chǎn)生Allee效應(yīng)。研究表明，除了捕食者的直接捕食行為會對食餌造成傷害，捕食行為對食餌產(chǎn)生的恐懼效應(yīng)還可以使食餌的增長速度降低40%，那么在繁殖過程中食餌就會由于覓偶困難而引起強Allee效應(yīng)[3]。近年來有學者對合作捕獲和恐懼效應(yīng)也進行了研究[4-5]，受此啟發(fā)，本文建立了一類捕食者合作捕獲對食餌產(chǎn)生恐懼效應(yīng)和強Allee效應(yīng)的模型，具體如下：

其中，x表示食餌的密度，y表示捕食者的密度，r是食餌的內(nèi)稟增長率，e是食餌對捕食者產(chǎn)生的恐懼因子，a表示合作強度參數(shù)，K是環(huán)境的容納量，A是食餌產(chǎn)生的強Allee效應(yīng)閾值，p是捕食者對食餌的攻擊率，c是捕食者的能量轉(zhuǎn)化率，m是捕食者的自然死亡率，所有參數(shù)皆為正值。為了簡化計算，對系統(tǒng)（1）進行無量綱化，令

去掉變量上的橫杠，得到如下模型：

這里由于Allee效應(yīng)的參數(shù)A小于環(huán)境容納量K，所以無量綱化后0 ＜b＜1。接下來，討論系統(tǒng)（2）的各類平衡點的存在性和穩(wěn)定性，并通過數(shù)值模擬驗證結(jié)論的可行性。

1 模型分析

1.1 平衡點的存在性

考慮代數(shù)方程組

系統(tǒng)（2）的平衡點為代數(shù)方程組（3）的非負解，系統(tǒng)（2）有邊界平衡點E0=(0,0)，E1=(b,0)和E2=(1,0)，其中E0表示滅絕平衡點，E1和E2表示沒有捕食者的邊界平衡點。接下來考慮內(nèi)部平衡點的存在條件。

定理1當cb＜m＜c時，系統(tǒng)（2）存在唯一的內(nèi)部平衡點。

證明現(xiàn)在考慮系統(tǒng)（2）的內(nèi)部平衡點，先將式（3）化簡為

記E*=(x*,y*)是系統(tǒng)（2）的內(nèi)部平衡點，那么有

由于ρ0、ρ1、ρ2、ρ3都是正值，而ρ4、ρ5的正負性不確定，因此考慮以下三個區(qū)域：

當式（5）所有的參數(shù)都在Ω1中，則有

即cb＜m＜c。因此，由笛卡爾定理[6]可知，當cb＜m＜c時，式（5）只有唯一的正解，那么系統(tǒng)（2）只存在唯一的內(nèi)部平衡點。

定理2當系統(tǒng)（2）的參數(shù)滿足下列任意一個條件：

（1）當a(1-b)＞1時，m＞c或m＜cb，

（2）當a(1-b)＜1時，m＞或m＜cb，

那么系統(tǒng)（2）存在兩個內(nèi)部平衡點。

證明當m＞時，有ρ4＜0；而當m＞c或m＜cb時，有ρ5＞0。下面討論與cb，b之間的關(guān)系。

（Ⅰ）當ab(b-1)＞1時，即，而0 ＜b＜1，所以不存在的情況。

（Ⅱ）當a(1-b)＞1時，即，這時系統(tǒng)（2）的參數(shù)a和b滿足a(1-b)＞1，參數(shù)m則需要滿足m＞c或m＜cb。那么當系統(tǒng)（2）的參數(shù)滿足a(1-b)＞1，m＞c或m＜cb時，有ρ4＜0，ρ5＞0。

（Ⅲ）當a(1-b)＜1時，即，這時系統(tǒng)（2）的參數(shù)a和b滿足a(1-b)＜1，參數(shù)m則需要滿足或m＜cb。那么當系統(tǒng)（2）的參數(shù)滿足a(1-b)＜1，或m＜cb時，有ρ4＜0，ρ5＞0。

由笛卡爾定理[6]可知，當系統(tǒng)（2）的所有參數(shù)都在Ω2時，式（5）存在兩個正解，那么系統(tǒng)（2）存在兩個內(nèi)部平衡點。

定理3當系統(tǒng)（2）的參數(shù)滿足下列任意一個條件：

（1）當a(1-b)＞1時，cb＜m＜，

（2）當a(1-b)＜1時，cb＜m＜c，

那么系統(tǒng)（2）不存在內(nèi)部平衡點。

證明當時，有ρ4＞0；當cb＜m＜c時，有ρ5＜0。由定理2 的證明可知不存在的情況，所以這里需要分兩種情況討論：

（Ⅰ）當a(1-b)＞1 且ab(b-1)＜1 時，即，由于0 ＜b＜1，那么參數(shù)a、b只考慮滿足a(1-b)＞1的情況，當系統(tǒng)（2）的參數(shù)滿足a(1-b)＞1，cb＜m＜時，有ρ4＞0，ρ5＜0。

（Ⅱ）當a(1-b)＜1時，即，這時系統(tǒng)（2）的參數(shù)a、b滿足a(1-b)＜1，當系統(tǒng)（2）的參數(shù)滿足a(1-b)＜1，cb＜m＜c時，有ρ4＞0，ρ5＜0。

由笛卡爾定理[6]可知，當系統(tǒng)（2）的參數(shù)都在Ω3時，式（5）不存在正解，系統(tǒng)（2）不存在內(nèi)部平衡點。

1.2 平衡點的穩(wěn)定性分析

定理4邊界平衡點E0是穩(wěn)定的結(jié)點；當c＜m，E1是鞍點，E2是穩(wěn)定的結(jié)點；當cb＜m＜c，E1，E2都是鞍點；當cb＞m，E1是不穩(wěn)定的結(jié)點，E2是鞍點。

證明E0、E1和E2的雅可比矩陣分別為

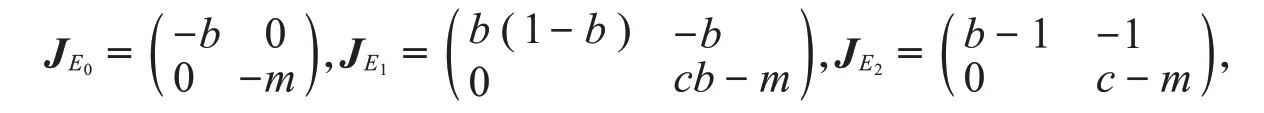
可以得出E0是穩(wěn)定的結(jié)點，由參數(shù)無量綱化可知0 ＜b＜1，所以b(1-b)＞0，b-1＜0。當c＜m時，cb-m＜0，c-m＜0，此時E1是鞍點，而E2是穩(wěn)定的結(jié)點。當cb＜m＜c時，E1、E2都是鞍點。當cb＞m時，E1是不穩(wěn)定的結(jié)點，而E2是鞍點。

定理5當內(nèi)部平衡點E*滿足Tr(JE*)＜0 且det(JE*)＞0 時，E*穩(wěn)定；當內(nèi)部平衡點E*滿足det(JE*)＜0時，E*不穩(wěn)定；當內(nèi)部平衡點E*滿足Tr(JE*)＞0且det(JE*)＞0時，E*不穩(wěn)定。

證明內(nèi)部平衡點E*(x*,y*)的雅可比矩陣是

并且對應(yīng)的特征方程是λ2-Tr(JE*)λ+det(JE*)=0，其中，

內(nèi)部平衡點的穩(wěn)定性取決于Tr(JE*)和det(JE*)的正負性，由Routh-Hurwitz 判據(jù)可知，當Tr(JE*)＜0且det(JE*)＞0時，內(nèi)部平衡點E*穩(wěn)定；而當det(JE*)＜0，或者Tr(JE*)＞0且det(JE*)＞0時，內(nèi)部平衡點E*不穩(wěn)定。

2 數(shù)值模擬

利用Matlab數(shù)值模擬來驗證邊界平衡點的穩(wěn)定性、內(nèi)部平衡點的存在性及穩(wěn)定性。

2.1 邊界平衡點的穩(wěn)定性

在定理4 的條件c＜m下，選取一組參數(shù)a=2，b=0.5，e=2，c=1，m=1.5，邊界平衡點E0=(0,0)，E1=(0.5,0)和E2=(1,0)如圖1中星號點所在位置，其對應(yīng)的相圖軌線如圖1所示。由圖1可知，E0和E2是穩(wěn)定的結(jié)點，E1是鞍點。

圖1 邊界平衡點的穩(wěn)定性

在定理4 的條件cb＜m＜c下，選取一組參數(shù)a=1，b=0.2，e=1，c=1，m=0.3，則邊界平衡點E0(0,0)，E1(0.2,0)和E2(1,0)如圖2中星號點所在位置，其對應(yīng)的相圖軌線如圖2所示。由圖2可知，E0是穩(wěn)定的結(jié)點，E1和E2是鞍點。

圖2 內(nèi)部平衡點和滅絕平衡點穩(wěn)定性

在定理4的條件cb＞m下，選取一組參數(shù)a=2，b=0.5，e=2，c=1，m=0.4，則邊界平衡點E0(0,0)，E1(0.5,0)和E2(1,0)如圖3中星號點所在位置，其對應(yīng)的相圖軌線如圖3所示。由圖3可知，E0是穩(wěn)定的結(jié)點，E1是不穩(wěn)定的結(jié)點，E2是鞍點。

圖3 滅絕平衡點穩(wěn)定性

2.2 內(nèi)部平衡點的存在性和穩(wěn)定性

方程組（4）在定理1的條件cb＜m＜c下，選取一組參數(shù)a=1，b=0.2，e=1，c=1，m=0.3，記方程組（4）的第一個和第二個方程分別為Function1和Function2，F(xiàn)unction1和Function2在這組參數(shù)下的圖像如圖4所示，它們在第一象限內(nèi)系統(tǒng)（2）只有唯一一個交點。由圖4可以清楚地看到，第一象限內(nèi)系統(tǒng)（2）只有一個內(nèi)部平衡點。

圖4 唯一內(nèi)部平衡點

借助Matlab 計算可知，這個內(nèi)部平衡點是E3（0.284 5，0.054 4），Tr(JE3)=0.1857 ＞0，det(JE3)=0.0216 ＞0，平衡點E3附近的相圖軌線如圖5所示。由圖5可以看到，E3是個不穩(wěn)定的結(jié)點，這和定理5的結(jié)論一致。

圖5 唯一內(nèi)部平衡點不穩(wěn)定

方程組（4）在定理2 的條件a(1-b)＞1，m＞c或m＜cb下，選取一組參數(shù)a=10，b=0.1，e=1，c=2，m=2.5，F(xiàn)unction1 和Function2 在這組參數(shù)下的圖像如圖6 所示，它們在第一象限內(nèi)有兩個交點。由圖6可以看到，第一象限內(nèi)系統(tǒng)（2）有兩個內(nèi)部平衡點。

圖6 兩個內(nèi)部平衡點

借助Matlab 計算可知，這兩個內(nèi)部平衡點分別是E4（0.651 8,0.091 7）和E5（0.949 3,0.031 6），Tr(JE4)=1.074 7 ＞0，det(JE4)=0.5413 ＞0 和det(JE5)=-0.308 8 ＜0，它們的相圖軌線如圖7 所示。由圖7可以清楚地看到，E4是不穩(wěn)定的結(jié)點，E5是鞍點，這和定理5的結(jié)論一致。

圖7 兩個內(nèi)部平衡點的穩(wěn)定性

3 結(jié)束語

綜上所述，本文建立了一類具有恐懼效應(yīng)和Allee效應(yīng)的合作捕食系統(tǒng)，分析并研究了平衡點的存在條件和穩(wěn)定性條件。從生態(tài)學角度來看，在具有恐懼效應(yīng)和Allee效應(yīng)的合作捕食系統(tǒng)中食餌與捕食者是可以共存的，避免了兩個物種其中一個滅絕或同時滅絕的情況發(fā)生。生物學中食餌與捕食者共存意味著生物的多樣性得以保留。生物的多樣性是生態(tài)平衡的主要因素，也是世界萬物繁衍生息的首要條件，生物多樣性同樣是人類社會得以生存和發(fā)展的根本。那么從這個角度來看，保護了生物的多樣性就等于保護了人類自身。