行NA陣列隨機和的弱收斂性

胡學平，王靜雅

（安慶師范大學數(shù)理學院，安徽安慶 246133）

Joag-Dev和Proschan[1]于1983年引入了NA列，定義如下。

定義[1]稱隨機變量X1,X2,X3,…,Xn(n≥2)是負相關（Negatively Associated，簡記為NA）的，若對{1,2,3,…,n}的任意兩個不交的子集A1，A2均有Cov(f1(Xi,i∈A1),f2(Xj,j∈A2))≤0，其中fi(i=1,2)是使上式有意義且對每個變元非降（或?qū)γ總€變元非升）的函數(shù)。如果對任意n≥2，X1,X2,X3,…,Xn是NA的，稱隨機序列{Xn,n≥1}是NA列。

Gut[2]證明了，對0 ＜p＜2，當時，有

其中，{an,n≥1}為常數(shù)列，這個結(jié)果已被推廣到許多不同情形，如文獻[3-6]。文獻[7]研究了行m-NA隨機陣列的完全收斂性，文獻[8-9]分別研究了行為NA列的矩完全收斂和矩完全收斂的等價條件。本文研究行NA陣列隨機指標部分和的弱大數(shù)定律，并推廣和改進文獻[2，4，5]中的結(jié)論。文中{Xnk,n≥1,k≥1}表示定義在同一概率空間的隨機變量陣列。I(A)為A的示性函數(shù)。約定c表示正常數(shù)，且在不同地方可以表示不同的值，即使在同一個式子中也如此。下面先給出相關引理。

引理1[1]設X1,X2,X3,…,Xn,n≥2為NA變量，A1,A2,A3,…,An是集合{1,2,3,…,n}的兩兩不交的非空子集，記αi=#(Ai)，表示集合A中的元素個數(shù)。如果fi:?αi→?(i=1,2,3,…,m)是m個對每個變元均非降（或?qū)γ總€變元非升）的函數(shù)，則f1(Xj,j∈A1),f2(Xj,j∈A2),f3(Xj,j∈A3),…,fm(Xj,j∈Am)仍為NA變量。此外，如果fi≥0，i=1,2,3,…,m，則還有

引理2[10]設隨機序列{Xn,n≥1}的p階矩存在，且當0 ＜p≤1時，它是任意隨機變量序列；當p＞1時，它是NA零均值序列，則對0 ＜p≤2，存在正常數(shù)c（只與p有關），使得

引理3[10]設X1,X2,X3,…,Xn為隨機變量，則

引理4設{an,n≥1}為一正的常數(shù)列，則對任意實數(shù)p，有

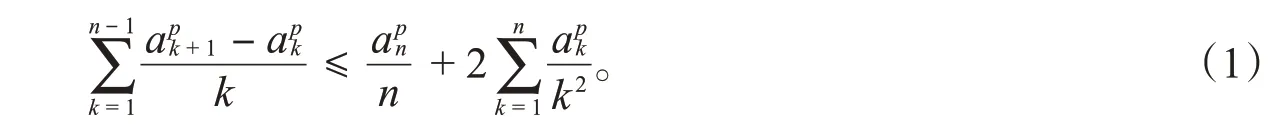
證明先證明式（1），有

根據(jù)式（1）及an/nδ，單增，當p=2時，有

從而式（2）得證。

下面給出本文的主要結(jié)論與證明。

定理1設{Xnk,n≥1,k≥1}是行NA陣列，{an,n≥1}為一正的常數(shù)列，且當時，滿足an/nδ單增，若

{Nn,n≥1}為一取正整數(shù)值的隨機變量列，且存在某個單增趨于無窮的正整數(shù)列{kn,n≥1}，滿足

因此只需證明Ii→0(i=1,2)，n→∞。對于I2，根據(jù)式（3）（4）有

下面證明I1→0，n→∞。令，根據(jù)式（4）可得

因此只需證明P(Bn)=o（1），根據(jù)Markov不等式、引理2和引理3，可得

根據(jù)引理4，{Tnj,n≥1,j≥1}是Toeplitz陣列，又根據(jù)式（3）和Toeplitz引理知式（7）的最后一項也趨向于0，從而定理1得證。

推論1在定理1中取，0 ＜p＜2，若，則有

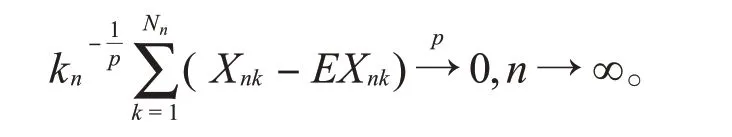
注特別當Nn=kn，m=kn時，NA列為鞅差序列[5]。

推論2設{Xnk,n≥1,k≥1}是一隨機變量陣列，{an,n≥1}為一單增正的常數(shù)列，且an=O(n)，若

{Nn,n≥1}為一取正整數(shù)值的隨機變量列，且對某個正整數(shù)l滿足P(Nn＞lan)=o(1)，則有

其中?n,j=σ{Xnk,1≤k≤j,j≥1,n≥1}。

注推論2為文獻[4]中的定理2，它是由鞅差序列得出的。本文定理對鞅差序列也成立，其證明的關鍵是引理2中的不等式對鞅差序列也成立，從而推廣了文獻[4]中的結(jié)論。

推論3設{Xnk,n≥1,k≥1}是行NA陣列，{an,n≥1}為單增正的常數(shù)列，且an=O(n)，若

{Nn,n≥1}為正整數(shù)值的隨機變量列，且滿足

證明由式（8），對充分大的n及?ε＞0，存在正常數(shù)l＞c+ε，使得