三角恒等變換常見典型考題賞析
■張文偉
三角恒等變換是高中數學的重要內容,也是高考的必考內容。三角恒等變換的公式多,如“同角三角函數的基本關系式”“正弦、余弦、正切的誘導公式”“兩角和與差的正弦、余弦、正切公式”“二倍角的正弦、余弦、正切公式”等,同學們要熟練掌握這些公式的正用、逆用和變形應用,要掌握三角恒等變換的解題規律和解題技巧。下面舉例解讀這部分的常見典型考題,供同學們學習與參考。
題型一:三角函數公式的應用
利用三角函數公式應注意的三點:(1)要注意公式的結構特點和符號變化規律,如兩角差的余弦公式可簡記為“同名相乘,符號相反”;(2)要注意同角三角函數基本關系、誘導公式的綜合應用;(3)要注意配方法、因式分解和整體代換思想的應用。


題型二:三角函數公式的逆用與變形應用

題型三:三角函數中的變“角”

題型四:三角函數中的變“名”
三角函數的名稱變換的關鍵是要明確各個三角函數名稱之間的聯系,常用到同角關系、誘導公式、弦化切或切化弦。轉化思想是三角恒等變換的主導思想,要從角的差異、函數名稱的差異、運算結構的差異中,尋求聯系,實現轉化。
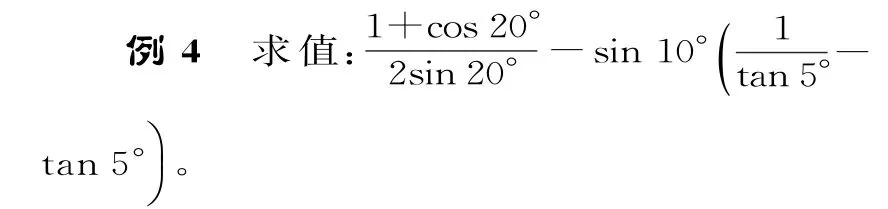

題型五:三角函數的化簡
三角函數的化簡遵循“三看”原則:一看“角”,這是最重要的一環,通過看角之間的差別與聯系,把角進行合理的拆分,從而正確使用公式;二看“函數名稱”,看函數名稱之間的差異,從而確定使用的公式,常見的有“切化弦”;三看“結構特征”,分析結構特征,可以幫助找到變形的方向,如“遇到分式要通分”。三角函數常見的基本變換方法有:異角化同角,異名化同名,異次化同次,降冪或升冪,“1”的代換,弦切互化等。

題型六:給角求值問題
對于給角求值問題,一般所給的角都是非特殊角,這時需要觀察所給角與特殊角之間的關系,利用三角變換轉化為求特殊角的三角函數問題。

題型七:給值求值問題
解答給值求值問題的三個基本步驟:(1)先化簡所求式子或所給條件;(2)觀察已知條件與所求式子之間的聯系;(3)將已知條件代入所求式子,化簡求值。


題型八:給值求角問題


題型九:三角函數中的參數范圍問題
求三角函數中的參數范圍問題,主要涉及三角函數的單調性、對稱性、周期性等。



題型十:三角函數的圖像與性質的綜合問題



題型十一:三角函數與平面向量的綜合問題
三角函數與平面向量的綜合問題的求解思路:利用向量平行(共線)或垂直關系得到三角函數式,再利用三角恒等變換進行化簡,最后結合三角函數的圖像與性質進行求解。及對應的θ值。


圖1

跟蹤訓練11:已知向量a=(cosx,sinx),b=(3,-3),x∈[0,π]。
(1)若a//b,求x的值。
(2)記函數f(x)=a·b,求函數f(x)的最大值和最小值及對應的x值。


