基于數值強度折減法的邊坡失穩判定方法

彭曉鋼 李 嘉 李有志 江 建

深圳市天健（集團）股份有限公司 廣東 深圳 518034

準確判斷邊坡的穩定性對路基、邊坡、基坑等工程非常重要，但是常規有限元分析方法難以直接評價邊坡穩定性，Zienkiewicz等[1]提出了強度折減法，該方法定義土體所能提供的最大抗剪強度和土體內實際剪應力之比為抗剪強度折減系數，計算時先取較小的折減系數Ftrial，保證開始時邊坡處于穩定狀態，然后逐漸增大折減系數Ftrial，直至Ftrial增大到某一值時邊坡處于極限狀態，即荷載引起的土體中實際剪應力恰好等于按照實際強度指標折減后的抗剪強度指標。Duncan[2]將邊坡安全系數定義為使邊坡剛好達到臨界破壞狀態時對土的剪切強度進行折減的程度，這一概念也就是傳統意義上的邊坡穩定安全系數。

強度折減法提出伊始受到計算條件的限制普及難度較大，Griffiths等[3]利用Fortran語言編寫有限元程序首次實現了邊坡強度折減法分析。隨著計算機硬件和數值軟件的發展，強度折減法愈加受到重視，很多巖土工程商業軟件中已經可以較為方便地應用強度折減法，如美國Itasca公司開發的FLAC、荷蘭Technical University of Delft開發的Plaxis、瑞士Zace Services公司開發的Z-SOIL.PC、韓國POSCO公司開發的Midas/GTS模塊等。

1 強度折減法在Abaqus軟件中的實現

Abaqus是當前應用最為廣泛的非線性有限元軟件之一，該軟件沒有提供強度折減法，但可以通過場變量的設置簡便地實現[4-6]。

強度折減法的基本原理實質就是強度參數c（黏聚力）、φ（內摩擦角）的逐漸降低導致土體強度不足以承擔當前應力，在有限元中即反映為強度參數c、φ的逐漸降低導致某單元應力超過了屈服面產生塑性變形，超出屈服面的應力將通過塑性變形傳遞到周圍土體單元，當應力超過屈服面的單元形成貫通的曲面時土體將失去穩定。

在Abaqus軟件中，可以通過設置強度參數隨場變量變化來實現強度折減，場變量沒有具體的物理意義，使計算分析更少受到人為假設的影響。在Abaqus軟件中，場變量Ffield隨時間增量步線性變化，材料參數和場變量之間有如下關系：

其中，c、φ是土體所能提供的抗剪強度指標，c'、φ'是某時間增量步下強度折減后土體的抗剪強度指標。

對比式（1）和式（2），土體到達極限狀態時的抗剪強度折減系數Ftrial和場變量Ffield有如下關系：

在Abaqus軟件計算過程中，場變量隨著增量步時間t而變化，通過設置材料參數隨場變量變化，實現材料強度折減過程。在Abaqus軟件中可實現增量步時間t的自動變化，進而實現強度的自動折減，并根據設定的破壞判據找到所對應的增量步時間，然后可得安全系數，并可得到相應的滑動面。

2 Abaqus軟件中強度折減法的失穩判定

正確判斷失穩狀態影響到強度折減有限元法得到的折減系數，進而影響安全系數的計算結果，強度折減有限元法的失穩判據主要有3類[7-8]，即：數值迭代不收斂判據、特征部位位移突變判據、廣義塑性應變或等效塑性應變貫通判據。

2.1 分析模型

為便于討論比較，以文獻[3]中的案例為對象，用Abaqus軟件進行強度折減有限元分析，對上述失穩判據進行對比。

Example1為均質邊坡，坡高H＝10 m，坡角β＝30°，土體重度γ＝20 kN/m3，黏聚力c＝5 kPa，內摩擦角φ＝30°。

建立邊坡有限元模型，幾何尺寸和文獻[3]中一致，坡頂和坡腳到模型邊界均取為12 m，坡腳以下土體厚度取10 m，假定彈性模量E＝100 MPa，為消除因網格劃分造成的計算結果誤差，采用和文獻[3]一致的網格劃分，采用縮減積分平面應變單元CPE4R。約束模型左右方向邊界的水平方向位移，底端邊界的水平方向和豎直方向位移。有限元模型如圖1所示。

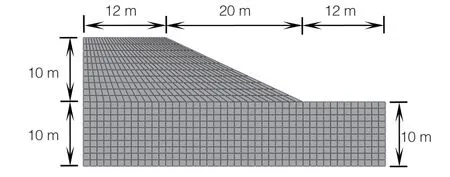
圖1 土坡強度折減有限元模型

對于實際計算邊坡安全系數的工程問題，強度折減系數Ftrial≥1，即根據土體實測強度指標進行強度折減，計算得到實際邊坡的安全系數。但對于有限元計算，不考慮實際意義，強度折減系數可以小于1，即折減系數起到擴大強度指標的作用，折減后強度指標反而更趨于安全。

計算分2步進行：第1步對邊坡施加豎直向下的重力，為使重力加載步順利完成，重力加載后多數區域處于彈性狀態，并使強度折減計算平穩過渡，采用Ftrial＝0.5時的參數，即黏聚力c＝10.0 kPa，內摩擦角φ＝49.0°；第2步對強度參數進行折減，設置最終狀態為Ftrial＝2.0，此時對應的土體強度參數為黏聚力c＝2.5 kPa，內摩擦角φ＝16.7°。

經過計算，可得不同泊松比v時的塑性區分布，如圖2所示。

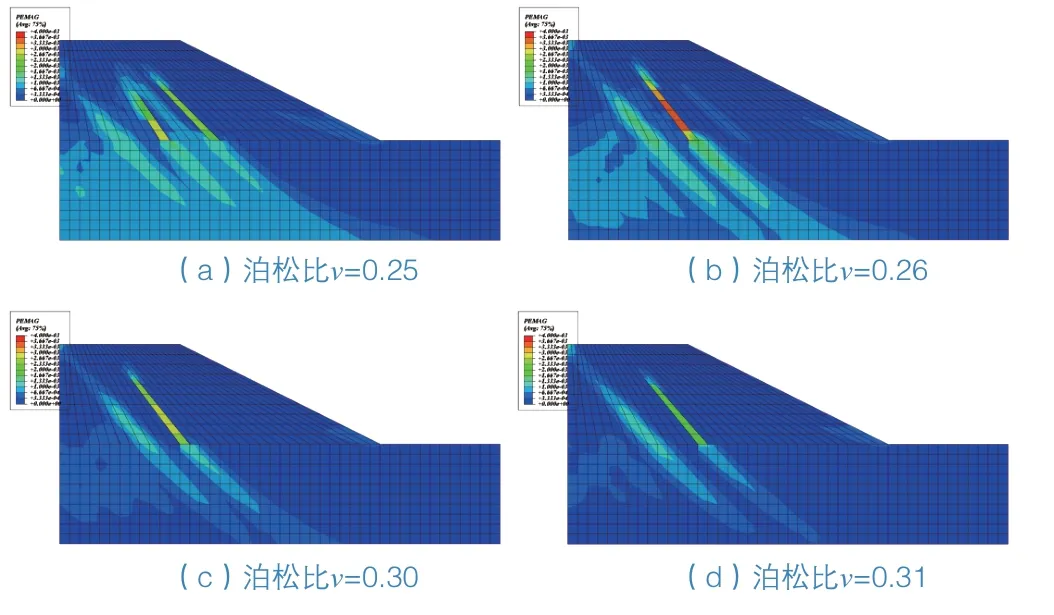
圖2 不同泊松比v時的塑性區分布

由圖2可知，泊松比取值對塑性區的分布有較大影響，泊松比取較小值時比取較大值時的塑性區范圍大，泊松比取較大值，直至計算因不收斂而終止時的塑性區范圍依然很小，但當泊松比取更小值時甚至會產生塑性區貫通的現象，因此采用廣義塑性應變或等效塑性應變貫通判據不能準確判斷土坡失穩。

有限元最后的總位移等值線包含了第1步中施加重力荷載引起的位移，無法判斷滑動面的位置，通過增量步之間的位移可反映邊坡失穩趨勢，計算采用最后2個增量步之間的位移進行判斷，計算得到最后一步的位移增量等值線云圖如圖3所示，根據圖3可判斷滑動面的位置，和圖4所示的文獻[3]中滑動面形狀對比也極為接近。

2.2 特征部位位移突變對邊坡失穩判定的影響

分別選取坡頂點和坡腳點作為特征點，將計算得到的強度折減系數Ftrial同特征點豎向位移U之間的關系繪制成曲線，如圖5所示。

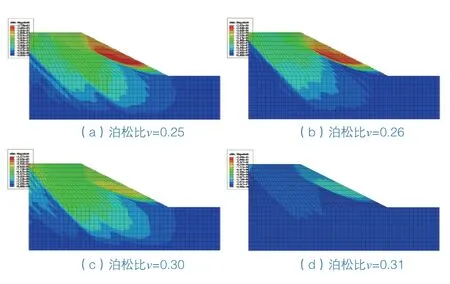
圖3 最后一步的位移增量等值線云圖

圖4 文獻[3]中的滑動面形狀

圖5 坡頂和坡腳特征點Ftrial-U關系曲線

由圖5可知，隨著強度折減系數增大，土體強度指標降低，直至計算因不收斂而終止，坡腳和坡頂特征點豎向位移均呈現較小泊松比時位移較大的規律，符合彈性理論。其中坡腳特征點豎向位移沒有明顯突變，較大泊松比時豎向位移還有略微減小的趨勢；坡頂特征點位移突變較明顯，然而位移突變點的強度折減系數差異較大，選取曲線水平段結束點作為突變點，強度折減系數Ftrial如表1所示。

表1 坡頂特征點位移突變點強度折減系數Ftrial

由表1可知，塑性區的分布會影響到坡頂特征點位移突變點的強度折減系數Ftrial，隨泊松比增大，塑性區范圍減小，由此判斷的強度折減系數Ftrial呈增大趨勢，且該方法需根據經驗判定位移突變點，沒有明確的指標作為判別依據，有一定的經驗誤差。

2.3 數值迭代不收斂對邊坡失穩判定的影響

將數值計算不收斂導致計算終止時的強度折減系數Ftrial匯總如表2所示。

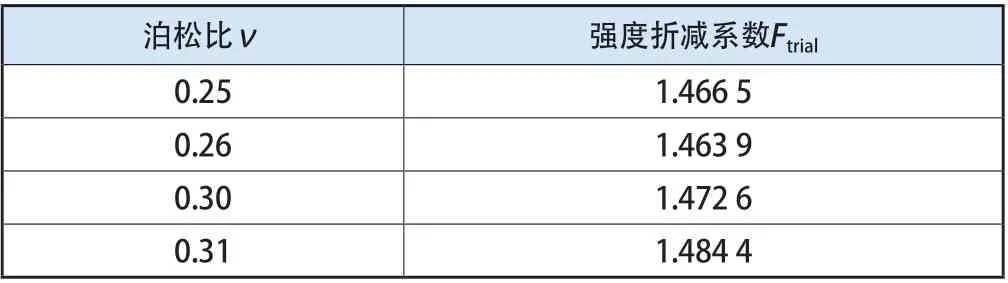
表2 不收斂終止時的強度折減系數Ftrial

由表2可知，隨泊松比的增大，雖然塑性區的分布發生了相應的變化，但計算因不收斂而終止時的強度折減系數Ftrial的差異很小，而且該方法無需根據經驗判定位移的突變點。

有限元中引起計算不收斂的因素有很多，有些學者質疑以數值計算不收斂作為邊坡失穩破壞依據是否存在其他人為導致的結果偏差，可通過對相同模型進行不同的設置并進行對比來說明這一問題。

該問題討論前首先要進行假設，即計算采用的有限元模型是正確的，如果模型建得不對或采用的有限元程序本身有缺陷，由此而引起的有限元數值計算不收斂本身就是毫無意義的。

上述模型計算采用的計算步長為1，初始增量步為0.1，最小增量步為1×10－5，其中最小增量步是判斷收斂與否的關鍵，將最小增量步進一步減小，分別設置為1×10－6和1×10－7，將計算結果進行對比如表3所示。

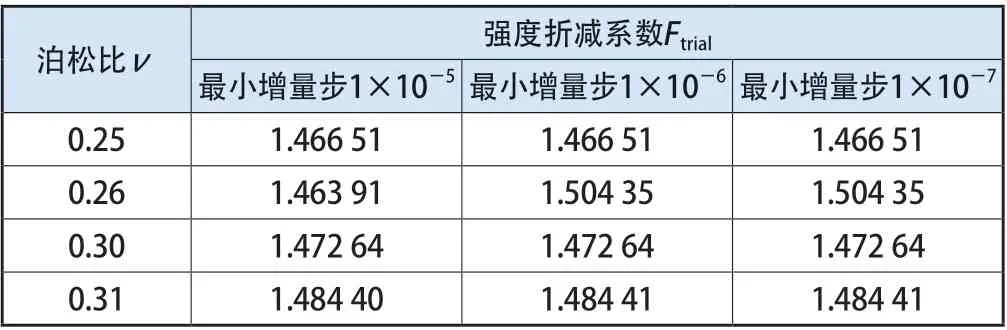
表3 收斂標準對計算結果的影響

Abaqus軟件中默認的最小增量步為1×10－5，在將最小增量步進一步調小至1×10－6和1×10－7后，計算因不收斂而終止時的強度折減系數變化不大，說明默認的增量步已可以保證足夠的計算精度，計算結果也表明有限元收斂條件的設置對結果影響不大，因此可以把有限元計算是否收斂作為邊坡失穩的判據。

3 結語

利用Abaqus軟件進行有限元強度折減計算的程序可靠，經過對數值迭代不收斂判據、特征部位位移突變判據、廣義塑性應變或等效塑性應變貫通3類判據的計算分析，得到如下結論：

1）泊松比取值對塑性區的分布有較大影響，泊松比取較小值時比取較大值時的塑性區范圍大，泊松比取較大值，直至計算因不收斂而終止時的塑性區范圍依然很小，但當泊松比取更小值時甚至會產生塑性區貫通的現象，因此采用廣義塑性應變或等效塑性應變貫通判據不能準確判斷土坡失穩。

2）塑性區的分布會影響到坡頂特征點位移突變點的強度折減系數Ftrial，隨泊松比增大，塑性區范圍減小，由此判斷的強度折減系數Ftrial呈增大趨勢，且該方法需根據經驗判定位移突變點，沒有明確的指標作為判別依據，有一定的經驗誤差。

3）數值計算是否收斂與邊坡是否失穩存在對應關系，計算因不收斂而終止時的強度折減系數變化不大，說明默認的增量步已可以保證足夠的計算精度，計算結果也表明有限元收斂條件的設置對結果影響不大，建議利用有限元計算收斂作為失穩判定的依據。