建筑群組合直線模式識別的模板匹配方法

行瑞星，武 芳，鞏現勇，杜佳威，劉呈熠

信息工程大學地理空間信息學院，河南 鄭州 450001

空間分布模式是指所關注地理要素在空間分布形態上呈現出能夠被識別且明確命名的形狀或排列[1-2]。結合人類認知特征挖掘矢量地圖數據中隱含的空間關系、結構和分布模式等知識，對于制圖綜合、時空數據挖掘等領域具有重要的理論意義和應用價值[1-5]。建筑群作為一類重要的地理要素，其隱含的空間分布特征，即本文的研究范疇，一直是制圖綜合領域研究的熱點和難點[6-8]。

當前，建筑群空間分布模式的研究主要關注兩個方面的問題[9]：一是模式的認知與定義，二是模式的識別和提取。建筑群空間分布模式定義是識別的前提和基礎，在不同的研究領域，模式的定義則有不同的依據[10]。根據建筑物的功能結構，文獻[11]提出工業/商業、市中心、市區、郊區和農村地區等5種模式。在制圖綜合領域，建筑群分布模式的分類和定義主要根據幾何特征和空間分布特征，文獻[12]將建筑群模式分為線型模式(直線型、曲線型和沿道路型等)和非線型模式(網格型和不規則型)。此外，有學者對建筑群字符型分布模式進行了研究[13-14]。建筑群分布模式識別提取的研究多集中于兩個步驟[4,15-17]：①基于空間鄰近的聚類；②基于視覺感知理論的空間分布特征多參數約束的模式識別。文獻[18]利用Delaunay三角網構建鄰近圖，通過對最小支撐樹進行反復修剪，實現直線模式和曲線模式的識別；文獻[19]結合結構化參數對鄰近圖進行異質性修剪，探測出多連通的直線模式，并通過圖論算法識別提取出網格模式。此外，還有采用深度學習的方法提取建筑群空間分布特征，文獻[20]利用圖卷積深度學習的方法提取了典型線型分布特征。直線模式識別作為一種空間數據增強方法，能有效挖掘建筑群的分布特征，為后續地圖綜合提供重要支持。然而，現有建筑群直線模式研究多關注于以單個建筑物為單元的同質性建筑群直線模式，對于大比例尺中建筑群局部異質性明顯但整體呈直線模式分布的現象則缺乏關注，當前尚未有學者對此問題進行深入研究。在識別建筑物分布模式時，不僅需要考慮同質性建筑群的直線分布模式，還需要考慮局部異質性明顯建筑群的直線分布模式，從而可以獲取更全面的建筑群空間分布模式。因此，為了解決具有局部異質性的建筑群直線模式識別問題，本文提出一種基于模板匹配的建筑群組合直線模式識別方法，主要解決兩個問題：①分析建筑群組合直線模式局部異質性的特點，提出多層次認知下建筑群組合直線模式的認知特征和定義；②采用模板匹配的策略解決局部異質性導致識別困難的問題,實現建筑群組合直線模式的提取。

1 建筑群組合直線模式的認知特征

建筑群的空間分布具有豐富的幾何結構模式，其結構特征的識別是人類對空間信息進行感知、識別和推理的過程[21]。如何使計算機“理解”人類對建筑群模式的空間認知規律，是建筑群模式自動識別的關鍵。

直線模式是建筑群的典型模式之一，大量認知研究表明直線模式的拓撲感知關系具有層次性[19]：從宏觀的層面看，模式群內建筑物有規律地呈直線分布；從微觀層面看，模式群內建筑物具有相似的特性(形狀、方向和大小等)。然而，上述直線模式的認知特征并不完全適用于具有局部異質性建筑群的直線模式。根據格式塔認知準則[4,15]、視知覺拓撲理論[22-23]，觀察者在觀看地圖時，首先，關注的是建筑物群整體空間分布，如圖1(a)中所框選的建筑群會被視為一個直線模式；其次，才會注意到局部的結構和特征，如圖1(b)所示，模式群內建筑物面積大小的差異會被明顯地感知到。雖然圖1(b)中部分建筑物之間具有明顯的特征差異，但在整體上仍可被識別為直線模式。針對這種整體具有同質性而局部存在異質性的直線模式，本文引入組合直線模式的概念進行定義。組合直線模式具有多層次認知的特點，在模式整體層，建筑群呈直線模式分布，在模式構件層，直線模式由具有相似特征的模式構件組成，在模式要素層，模式構件為單個建筑物要素或由多個建筑物要素組合而成。與一般直線模式強調單個建筑物之間的同質性不同的是，組合直線模式需要考慮存在兩個或多個鄰近建筑物被視作一個整體(記為組合建筑物)的情況。若建筑群內存在組合建筑物，且組合建筑物作為整體與其他建筑物或組合建筑物形成直線模式，則該建筑群呈組合直線模式分布。

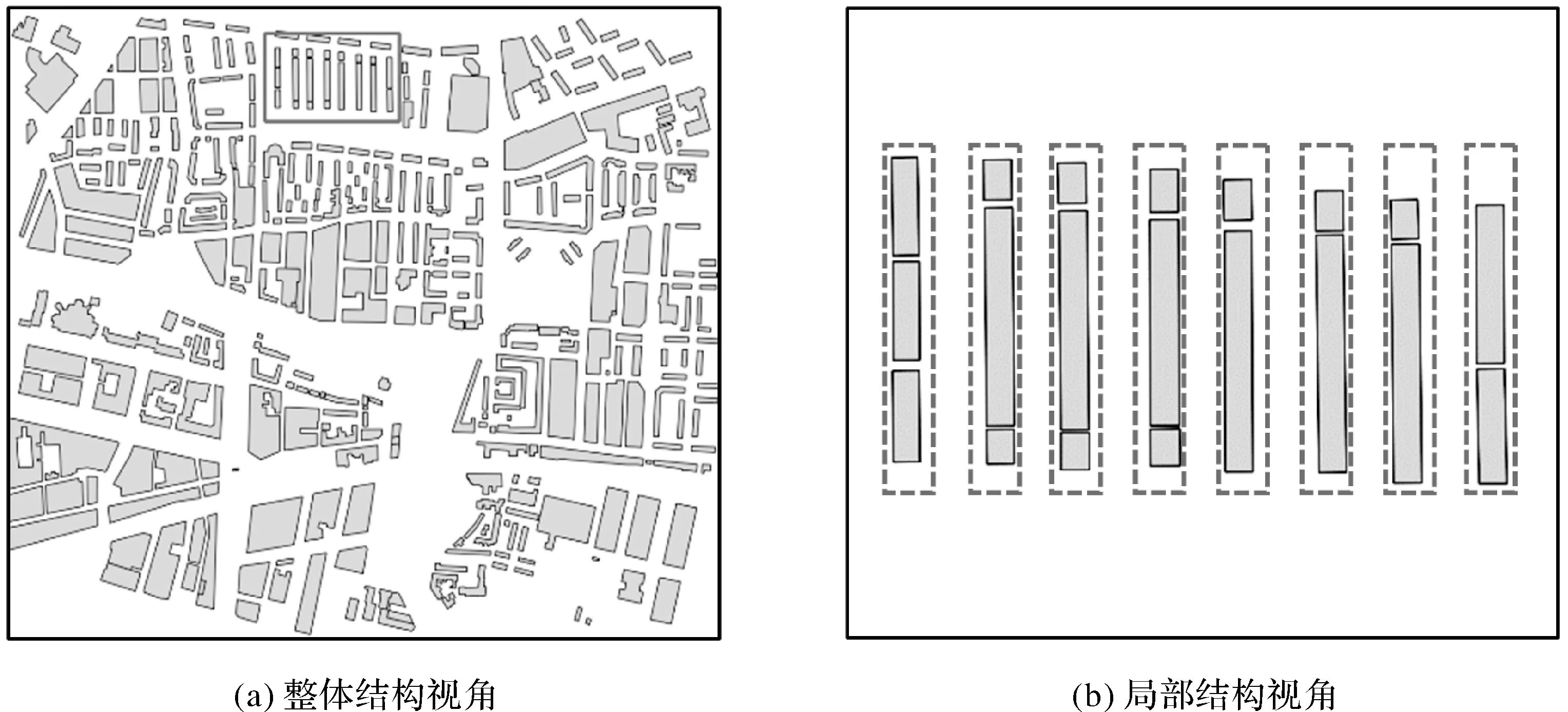
圖1 整體到局部的感知認知Fig.1 The perception and cognition from whole to part

文獻[4]提出了建筑物的擴展對齊分布，即如果兩個建筑物的中心連線平行于兩個建筑物最小面積外接矩形(smallest minimum bounding rectangle,SMBR)的長軸，則兩個建筑物構成擴展對齊分布。分析可知，能進行組合并形成直線模式的建筑物具有形狀規則、矩形度[24]高的特點，而且可以互相作為沿主方向(長軸方向)擴展延伸的部分，同時在與主方向垂直的維度具有相似的尺寸(短軸長度)。那么，可組合的建筑物一定呈擴展對齊分布。此處，對文獻[4]定義的擴展對齊分布進行補充，即如果兩個建筑物的中心連線分別平行于其SMBR的長軸，且SMBR的短軸長度相似，則構成擴展對齊分布。構成擴展對齊分布是相鄰建筑物作為組合建筑物形成組合直線模式的必要條件。為區別于組合直線模式，本文將不考慮建筑物組合情況的直線模式稱為簡單直線模式。

從相鄰模式構件中建筑物空間對應關系的角度看，簡單直線模式只包含1∶1的空間對應關系，而組合直線模式中則包含1∶1、1∶n和m∶n相互組合的空間對應關系。因此，組合直線模式識別的過程可以看作是建立建筑物與所屬模式構件之間1∶1或n∶1以及模式構件之間1∶1空間對應關系的過程，即建筑物由“建筑物—模式構件—直線模式”的組織過程。

綜上分析，本文提出一種基于模板匹配的組合直線模式識別方法：首先，根據待識別的(組合)建筑物構建一組呈直線模式分布的模板，如圖1(b)中的虛線矩形框為構建的模板；然后，通過模板與建筑物進行匹配來建立空間對應關系，識別出由模板對應建筑物組成的模式構件，即識別出由模式構件形成的直線模式，如圖1(b)中每個模板內的建筑物為匹配的對應建筑物，各模板對應建筑物組合而構成模式構件，而多個模式構件形成組合直線模式。

2 基于模板匹配的組合直線模式識別

人作為認知主體自然地以有組織的模式感知空間場景遵循格式塔認知準則，主要包括：鄰近性、相似性、連續性、封閉性、連通性和共同區域等6個原則[15-17]。對于建筑群，封閉性、連通性和共同區域可由鄰近性代替，因此在建筑群模式識別時，主要考慮鄰近性、相似性和連續性[19,25]。考慮到組合直線模式的直線性、相似性和局部異質性等特點，結合人類視覺格式塔認知準則，從建筑物的形狀、大小和方向建立認知意義上的結構化參數(表1)，作為組合直線模式提取的約束條件。

表1 組合直線模式結構化參數

本文采用“自頂向下”與“自底向上”相結合的策略進行組合直線模式的識別提取：首先基于建筑物鄰近性、尺寸和方向約束進行聚類，獲得建筑物空間鄰近關系和擴展對齊關系；然后，構建建筑群直線模式的連續匹配模板，以所建的模式結構化參數為約束，最終實現組合直線模式的提取。

2.1 構建建筑物空間鄰近關系及擴展對齊關系

建筑物的空間鄰近及擴展對齊關系構建作為直線模式識別提取的數據準備階段，主要提供空間數據模型支撐。建筑物的空間鄰近性是其構成直線模式的必要條件，鄰近關系的構建是建筑群模式識別的首要任務。本文采用約束Delaunay三角網構建建筑物鄰近關系，構網之前需要對建筑物邊界進行內插加密。根據第1節分析可知，只有呈擴展對齊分布的建筑物才有可能形成組合直線模式，建筑物擴展對齊關系的確定是組合直線模式識別提取的前提。擴展對齊關系可在空間鄰近關系的基礎上獲取，具體步驟如下：

(1) 構建建筑群的CDT，獲取鄰近關系并進行記錄。

(2) 選擇CDT中任意一條連接不同建筑物的邊Ei，獲取Ei所連接建筑物A、B的SMBR長軸及短軸，計算建筑物A、B中心連線與建筑物A、B的長軸夾角θA、θB，計算建筑物A、B短軸的長度比Rwid，如果θA、θB、Rwid同時滿足式(1)的條件

(1)

式中，δori和δwid分別為人工設定的方向差和長度比的閾值。則兩個建筑物構成擴展對齊分布，并進行記錄；否則，兩個建筑物不構成擴展對齊分布，刪除邊Ei。

(3) 重復執行步驟(2)，直至遍歷完整個CDT，獲得建筑物擴展對齊分布聚類結果(圖2)。

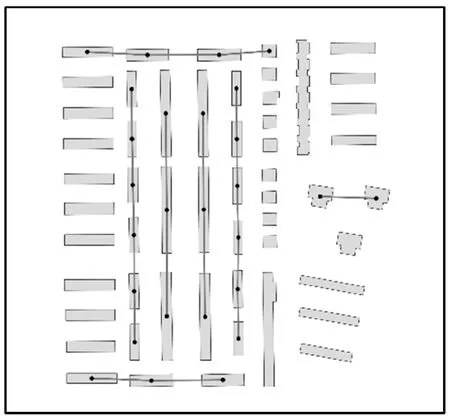
圖2 擴展對齊分布聚類結果Fig.2 Clustering result of extension alignment

根據面向對象的編程思想，可以構建建筑物空間關系的數據結構，Neighbor結構體如下所示。

public struct Neighbor

{

Public IFeature building; ∥建筑物要素

Public IPolygon building_SMBR;∥建筑物的最小面積外接矩形

PublicList building_Neighbor;∥空間鄰近的建筑物ID

Public int building_Extend1;∥擴展對齊的建筑物ID

Public int building_Extend2; ∥擴展對齊的建筑物ID

…… ∥其他成員變量

}

注：一個建筑物最多存在兩個直接鄰近且呈擴展對齊分布的建筑物。

2.2 構建初始匹配模板

本文構建匹配模板的思路是首先根據待識別的(組合)建筑物確定初始匹配模板的幾何特征(形狀、尺寸)，然后根據初始匹配模板連續構建形狀、尺寸相同且呈等間隔直線分布的模板來搜索、匹配待識別的建筑物。初始匹配模板的幾何特征由待識別(組合)建筑物決定。由于組合直線模式中建筑物與模式構件有1∶1和n∶1的空間對應關系，因此，在構建初始匹配模板時需要考慮兩種情況：①以單個建筑物為搜索起點構建匹配模板，如圖3(a)中建筑物A；②以組合建筑物為起點構建匹配模板，如圖3(b)中建筑物A和B組成的組合建筑物。考慮到組合直線模式的模式構件為形狀規則、矩形度高的(組合)建筑物，因此本文以(組合)建筑物的SMBR作為匹配模板。模式識別過程中，根據匹配模板與建筑物的空間關系可以初步篩選出待識別的建筑物候選集合，為了適當擴大模板匹配范圍，需要對提取的SMBR進行一定程度的放大，將放大后的SMBR作為初始匹配模板，如圖3(a)、(b)中虛線框所示。

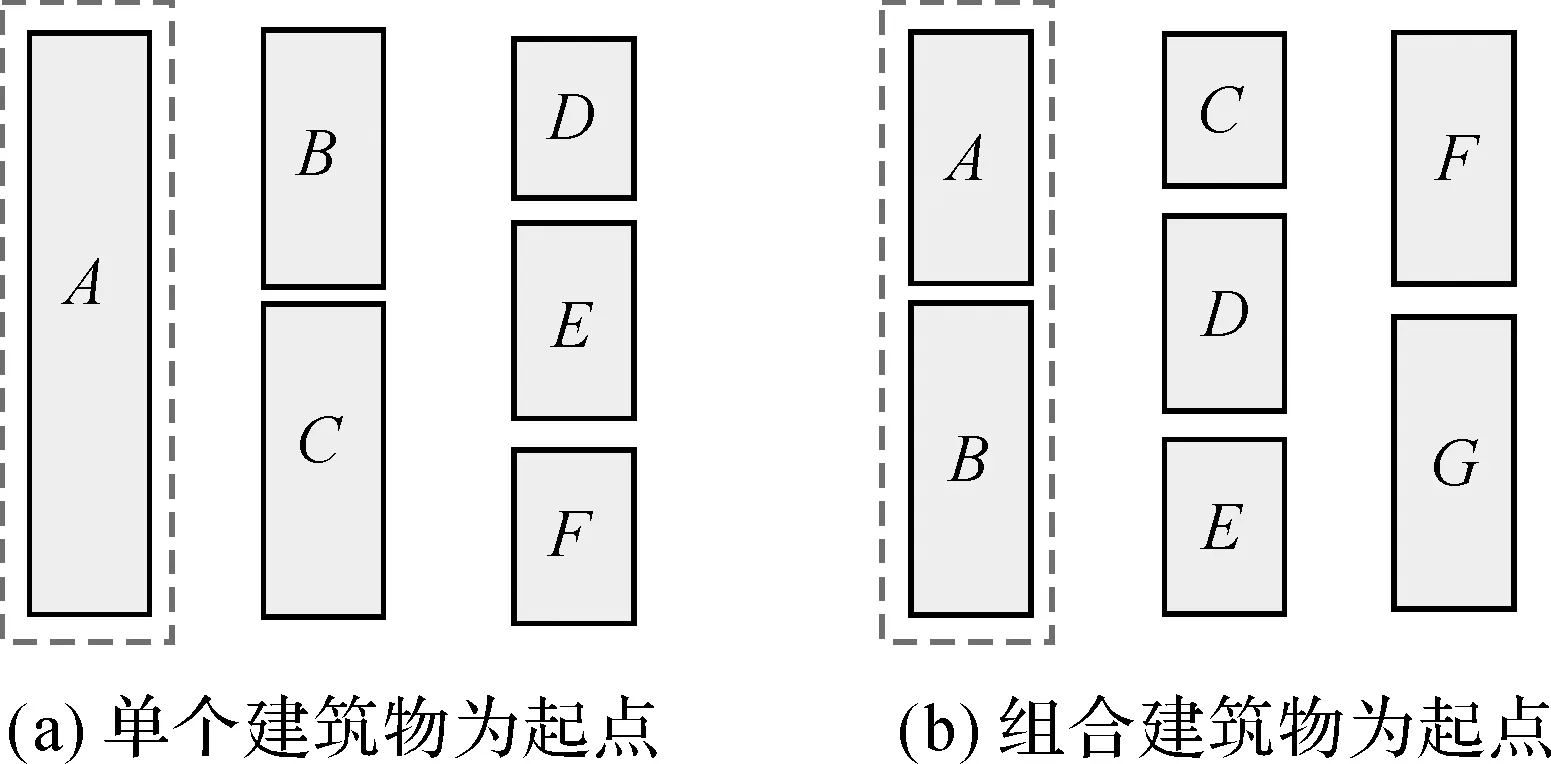
圖3 初始匹配模板構建Fig.3 Construction of initial matching template

2.3 確定模板的分布間隔和方向

根據初始匹配模板連續構建形狀、尺寸相同且呈等間隔直線分布模板的關鍵是確定模板的分布間隔和方向，根據典型的建筑群直線模式分布特征可知，模式中任意兩個直接鄰近建筑物的分布間隔和方向(質心連線方向)可以反映整個直線模式內建筑物的分布特征。本文利用錨點來表達相鄰建筑物的分布特征(間隔、方向)，結合圖4所示，設圖4(a)中的矩形SA(A1A2A3A4)和SB(B1B2B3B4)是相鄰建筑物A和B的SMBR，相鄰建筑物錨點的獲取步驟如下：

(1) 將矩形SA和SB以各自幾何中心OA和OB為基準點進行疊置(圖4(b))。

(2) 分別計算矩形SA的頂點A1、A2、A3和A4到矩形SB所有頂點之間的距離。

(3) 分別取距離最近的一組頂點記為錨點，如圖4(b)中用虛線連接的點對，如點A1與B1之間的距離較其他SB上頂點最近，則A1與B1為一組錨點。

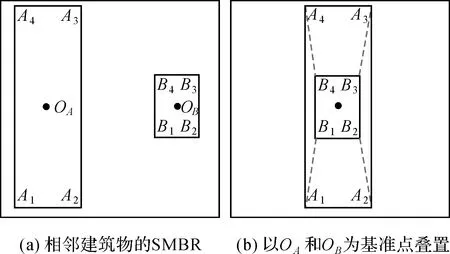
圖4 獲取相鄰建筑物錨點Fig.4 Obtaining anchor points of adjacent buildings

分析可知，對于兩個大小、形狀相似且主方向一致的建筑物，以錨點為基準進行疊置則兩個建筑物的重合面積與自身面積基本相等。結合典型直線模式認知特征可知，模式內兩個相鄰建筑物的任一組錨點間距可以表達模式內建筑物的分布間隔，而其連線的方向則表達了模式內建筑物的分布方向。因此，可以根據起始建筑物和相鄰建筑物之間錨點計算出后續匹配模板的位置。如果相鄰建筑物與其擴展對齊的建筑物能以組合的形式作為組合直線模式構件，雖然起始建筑物與該鄰近建筑物之間的不同錨點表達不同分布特征的模板，如圖5(a)、(b)所示，但肯定存在一組可以表達該模式內建筑物空間分布特征的錨點。因此本文分別取該鄰近建筑物SMBR任一對角線上的兩個端點獲取錨點，并以此分別構建后續的匹配模板，如圖5所示，頂點B1和B3是一條對角線的端點，分別以A1、B1和A3、B3組成錨點，可構建出不同分布特征的匹配模板。

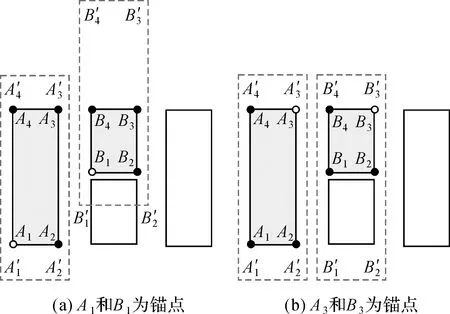
圖5 根據不同錨點構建匹配模板Fig.5 Matching templates based on different anchor points

(2)

(3)

根據新模板的頂點坐標和式(3)不斷計算出后續模板的頂點坐標。

2.4 建筑群組合直線模式提取

本文所提模式識別方法主要根據初始匹配模板連續構建形狀、尺寸相同且呈等間隔直線分布的模板來搜索、匹配待識別建筑物，同時結合約束條件來判定待識別的建筑物能否組成直線模式。結合上述模式提取關鍵步驟，記建筑物Pi的矩形度為Rec(Pi)，Pi與模板M的面積重合度為OLarea(Pi,M)，Pi與鄰近建筑物Pj的局部方向差異為LDorient(Pi,Pj)，長軸長度比、短軸長度比為Rlen(Pi,Pj)、Rwid(Pi,Pj)，Pi與已匹配建筑物的整體方向差異為ODorient(Pi)，設矩形度、模板重合度、長軸長度比、短軸長度比、方向差異的閾值分別為δrec、δarea、δlen、δwid、δori。本文利用模板匹配方法識別建筑群組合直線模式的整體步驟如下。

(1) 根據2.1節方法獲取建筑物間的空間鄰近和擴展對齊關系。

(2) 選取任一建筑物或由k個建筑物組成的組合建筑物作為起始建筑物Ps(k=2,3,…n；n代表空間數據中存在最多包含n個兩兩直接鄰近且呈擴展對齊排列建筑物的組合建筑物)，如果Rec(Ps)>δrec，則構建初始匹配模板，將Ps記錄到模式鏈表Pattern，執行步驟(3)；否則執行步驟(2)，直到遍歷完所有建筑物和組合建筑物，執行步驟(8)。

(3) 選取任一與Ps直接鄰近的建筑物Pn，如果Rec(Pn)>δrec且LDorient(Ps,Pn)<δori，則執行步驟(4)；否則，執行步驟(3)，直到遍歷完所有直接鄰近建筑物，執行步驟(2)。

(4) 計算出Ps與Pn的兩組錨點，根據錨點和起始匹配模板分別構建出新的模板Mnew，分別執行步驟(5)。

(5) 如果OLarea(Pn,Mnew)<δarea，則執行步驟(2)；否則，判斷Rlen(Ps,Pn)、Rwid(Ps,Pn)，如果Rlen(Ps,Pn)>δlen且Rwid(Ps,Pn)>δwid，將Pn記錄到直線模式鏈表Pattern中，執行步驟(7)；如果Rlen(Ps,Pn)<δlen或Rwid(Ps,Pn)<δwid，則將Pn記錄到數組PList，執行步驟(6)。

(6) 搜索與Pn擴展對齊的鄰近建筑物Pe，如果不存在Pe則執行步驟(2)；如果OLarea(Pe,Mnew)<δarea，則執行步驟(2)；否則，將Pe記錄到數組PList，計算數組PList內所有建筑物長軸之和、短軸均值分別與Ps的長軸、短軸的長度比Rlen、Rwid，如果Rlen<δlen或Rwid<δwid，則將建筑物Pe標記為Pn，執行步驟(6)；否則，將數組PList內所有建筑物視為一個組合建筑物Pc，如果ODorient(Pc)<δori，則將PList記錄到直線模式鏈表Pattern中，執行步驟(7)；否則，則執行步驟(2)。

(7) 根據錨點和模板Mnew構建出新的模板并標記為Mnew，遍歷Pattern中最后一個建筑物Pl直接鄰近的建筑物并標記為Pn，如果Rec(Pn)>δrec且LDorient(Pl,Pn)<δori，則執行步驟(5)；否則，執行步驟(2)。

(8) 刪除所有不包含組合建筑物的模式，去除完全重復的模式。

此外，上述步驟經過少量適當修改后，可適用于提取簡單直線模式。

下面以圖6所示的建筑物為例說明本文組合直線模式識別方法。設A為起始建筑物，選擇與A直接鄰近且滿足局部方向差異和矩形度約束的建筑物B為待匹配對象，計算建筑物A和B兩組呈對角線分布的錨點，根據起始模板MA1分別構建出模板MB1和MB2，如圖6(a)所示；選擇以MB1為搜索匹配方向，如圖6(b)所示，建筑物B與模板的面積重合度大于閾值，但與建筑物A長軸長度比小于閾值，因此選擇與建筑物B形成擴展對齊且與模板MB1面積重合度大于閾值的建筑物C為待組合對象，建筑物B、C的長軸之和、短軸均值分別與建筑物A的長軸、短軸長度比大于閾值，因而將建筑物B、C視為組合建筑物(圖6(c))并將B和C記入模式鏈表，至此，模板MB1的建筑物匹配完成；根據錨點與模板MB1構建出模板MD1，如圖6(c)所示，遍歷與建筑物B、C直接鄰近且符合局部方向差異和矩形度約束的建筑物，選擇與模板MD1面積重合度大于閾值的建筑物D，因為建筑物D與A的長軸、短軸長度比大于閾值，將D記入模式鏈表，如圖6(d)所示；選擇以MB2為匹配方向則無符合要求的建筑物。至此，以建筑物A為起點最終識別出一組組合直線模式。

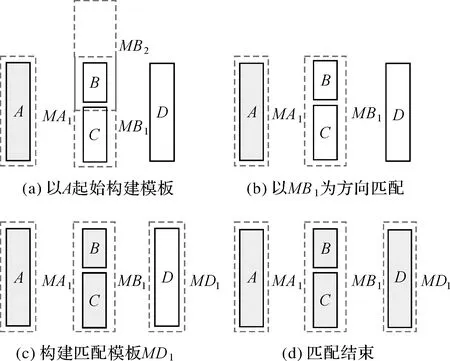
圖6 組合直線模式識別過程Fig.6 Process of combined collinear pattern recognition

3 試驗與討論

3.1 試 驗

為驗證本文算法的有效性，使用C#和ArcGIS Engine編程實現了以上算法。為更好體現所提算法的合理性和適用性，試驗分為兩組，采用兩組不同尺度和不同空間分布特點的數據進行試驗，同時加入了簡單直線模式提取的對比試驗。本文組合直線模式提取方法的整體過程涉及多個參數閾值，參數閾值設置的總體思路為：矩形度、長度比和模板重合度的閾值越大(經驗取值[0.6,1])，放大倍數越小，方向差異的閾值越小(經驗取值[0°,10°])，則模式的直線性、同質性越強。

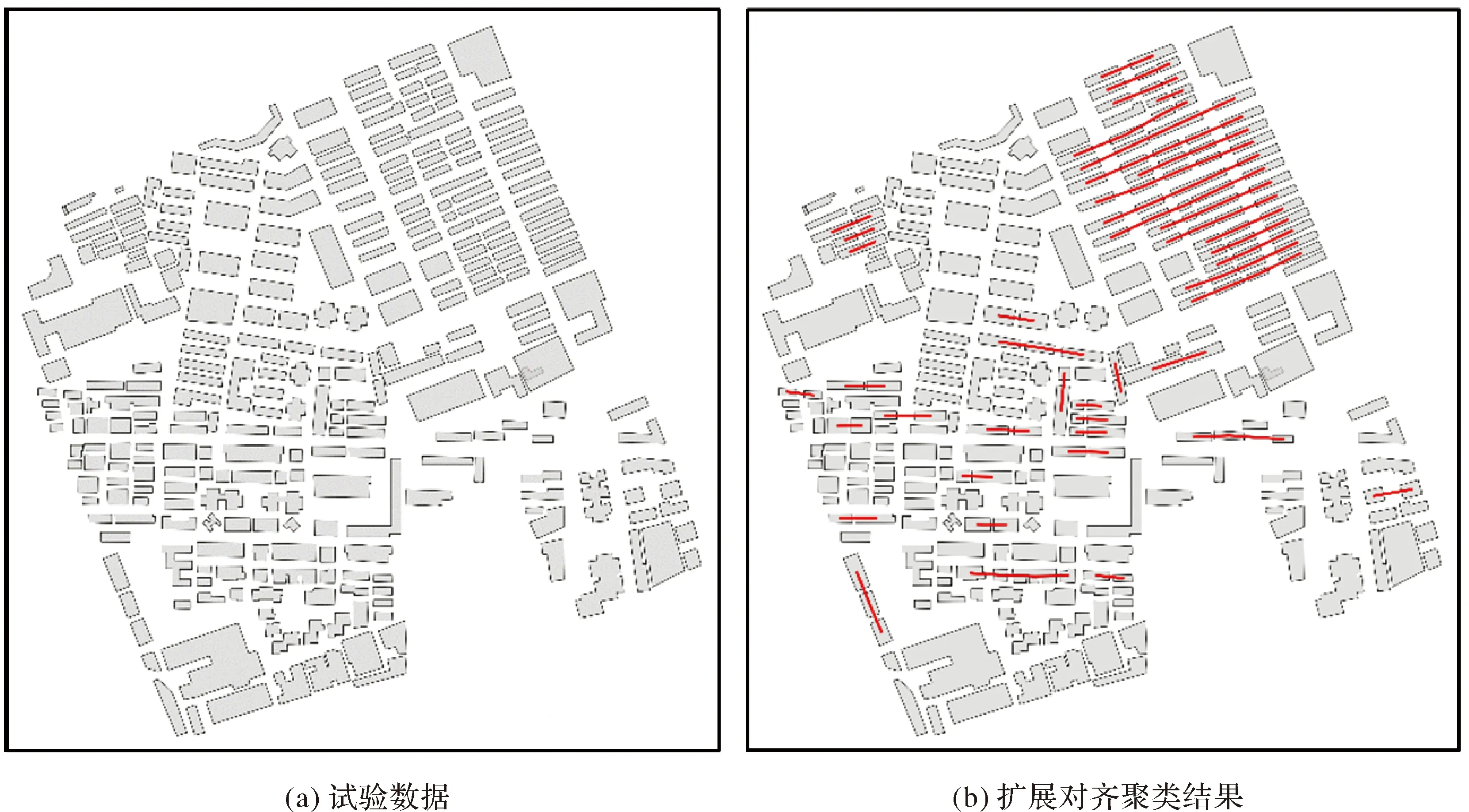
試驗數據1為荷蘭鹿特丹(Rotterdam，the Netherlands)地區1∶10 000比例尺的部分建筑群，試驗區域總共包含612個建筑物，如圖7(a)所示。所選試驗區域建筑物的大小和形狀具有一定的差異性，多數建筑物分布方向近似，且形狀規則、矩形度高，建筑群局部分布密集，存在明顯的局部空間異質性，在視知覺上呈現出明顯的組合直線模式。參考前人經驗[18-19]，經過反復測試，參數設置見表2，擴展對齊分布聚類如圖7(b)所示，識別提取的組合直線模式如圖7(c)所示，識別提取的簡單直線模式如圖7(d)所示。

試驗數據2為中國廣州市區的局部建筑群，數據來自OpenStreetMap，比例尺為1∶5000，試驗區域總共包含288個建筑物，如圖8(a)所示。所選試驗區域多數建筑物形狀規則、矩形度高，建筑群整體分布密集，沒有全局平穩的特征，一階鄰域內要素的面積變化較大，有明顯的空間異質性，但在某些局部區域存在較為平穩的特征，因此在視知覺上呈現出明顯的組合直線模式。參數設置如表2，擴展對齊分布聚類如圖8(b)所示，識別提取的組合直線模式如圖8(c)所示，識別提取的簡單直線模式如圖8(d)所示。圖7、圖8中虛線為每個組合建筑物內相鄰建筑物幾何中心的連線，用以表示由組合建筑物形成的模式構件，實線為每個直線模式內相鄰模式構件即建筑物或組合建筑物的幾何中心連線，用以表示由模式構件形成的直線模式。

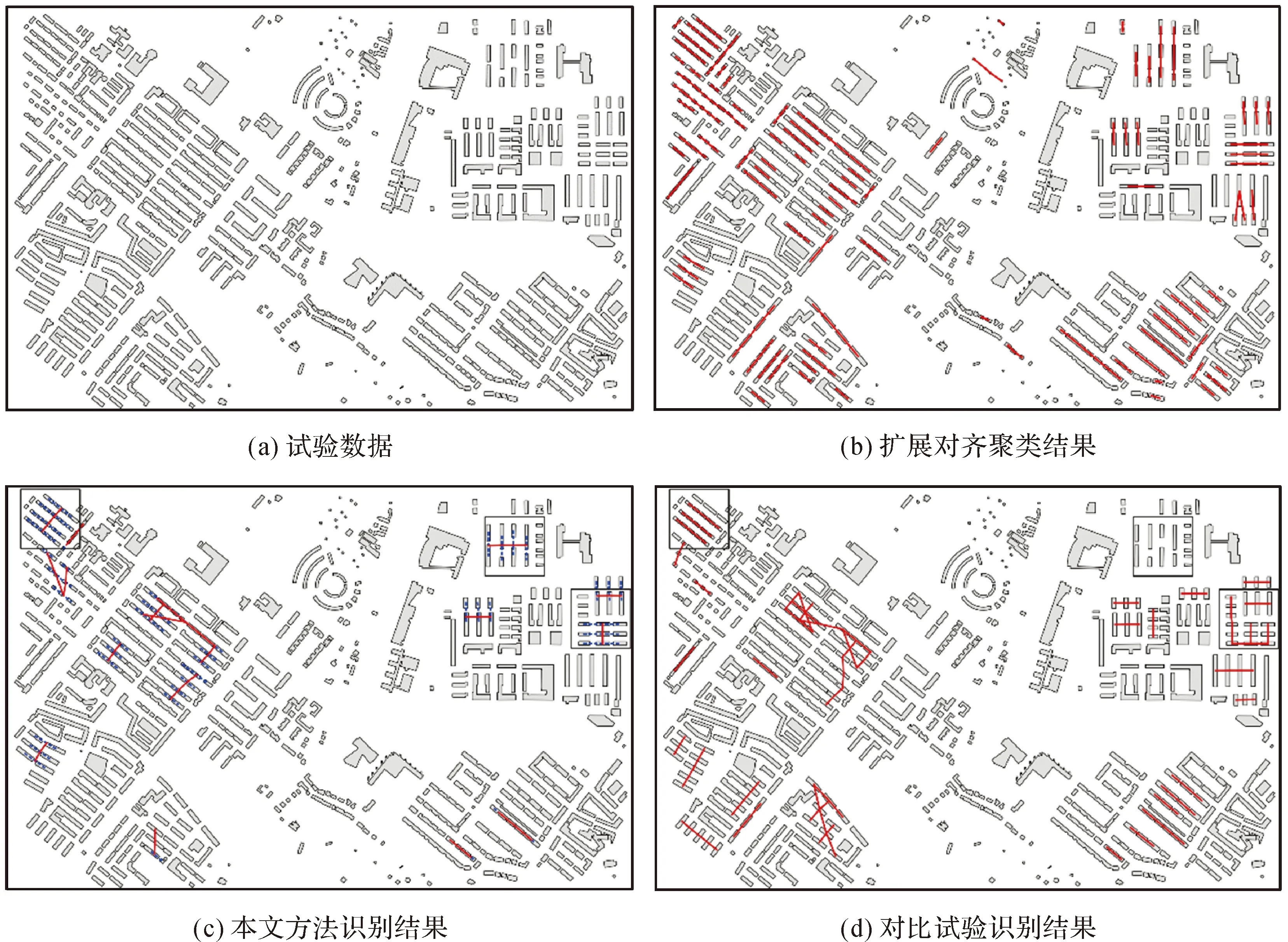
圖7 組合直線模式識別試驗結果Fig.7 Experiment result of combined collinear pattern recognition

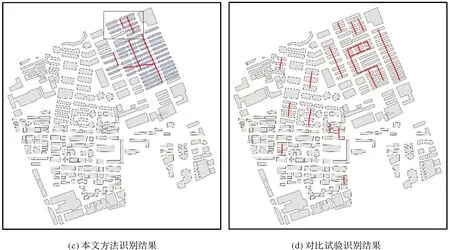
圖8 組合直線模式識別試驗結果Fig.8 Experiment result of combined collinear pattern recognition

表2 參數設置

對試驗1的結果進行統計、對比分析可知，本文方法提取出18個組合直線模式，對比試驗提取出46個簡單直線模式，本文提取的組合直線模式中有15個與對比試驗結果中29個簡單直線模式存在相交或者包含的關系。其中有23個簡單直線模式分別包含于12個組合直線模式，例如，圖9(d)中的3個簡單直線模式1、2、3分別作為模式構件完全包含于圖9(a)中的組合直線模式1。其余6個簡單直線模式與9個組合直線模式存在相交的關系，例如，圖9(e)中簡單直線模式1內有3個建筑物分別與其他建筑物組合成模式構件，形成圖9(b)中的組合直線模式2。此外，本文方法提取出3個與簡單直線模式無關聯建筑物的組合直線模式，例如，圖9(c)中形成組合直線模式的建筑物在圖9(f)中與簡單直線模式無關聯。本文方法識別提取的組合直線模式基本符合“建筑物—模式構件—組合直線模式”的多層次認知特點，如圖9(a)中以簡單直線模式作為模式構件和圖9(c)中由面積大小差異明顯建筑物組合成模式構件，進而由多個具有相似特征的模式構件形成組合直線模式。對試驗2的結果進行統計、對比分析可知，本文方法提取出6個組合直線模式，對比試驗提取出21個簡單直線模式，提取的所有組合直線模式與對比試驗結果中13個簡單直線模式存在相交或者包含的關系。分析可知，現有研究的直線模式認知特征和識別方法并不適用于組合直線模式，而本文所提方法則可以識別出局部異質性明顯的建筑群內涵的組合直線模式。

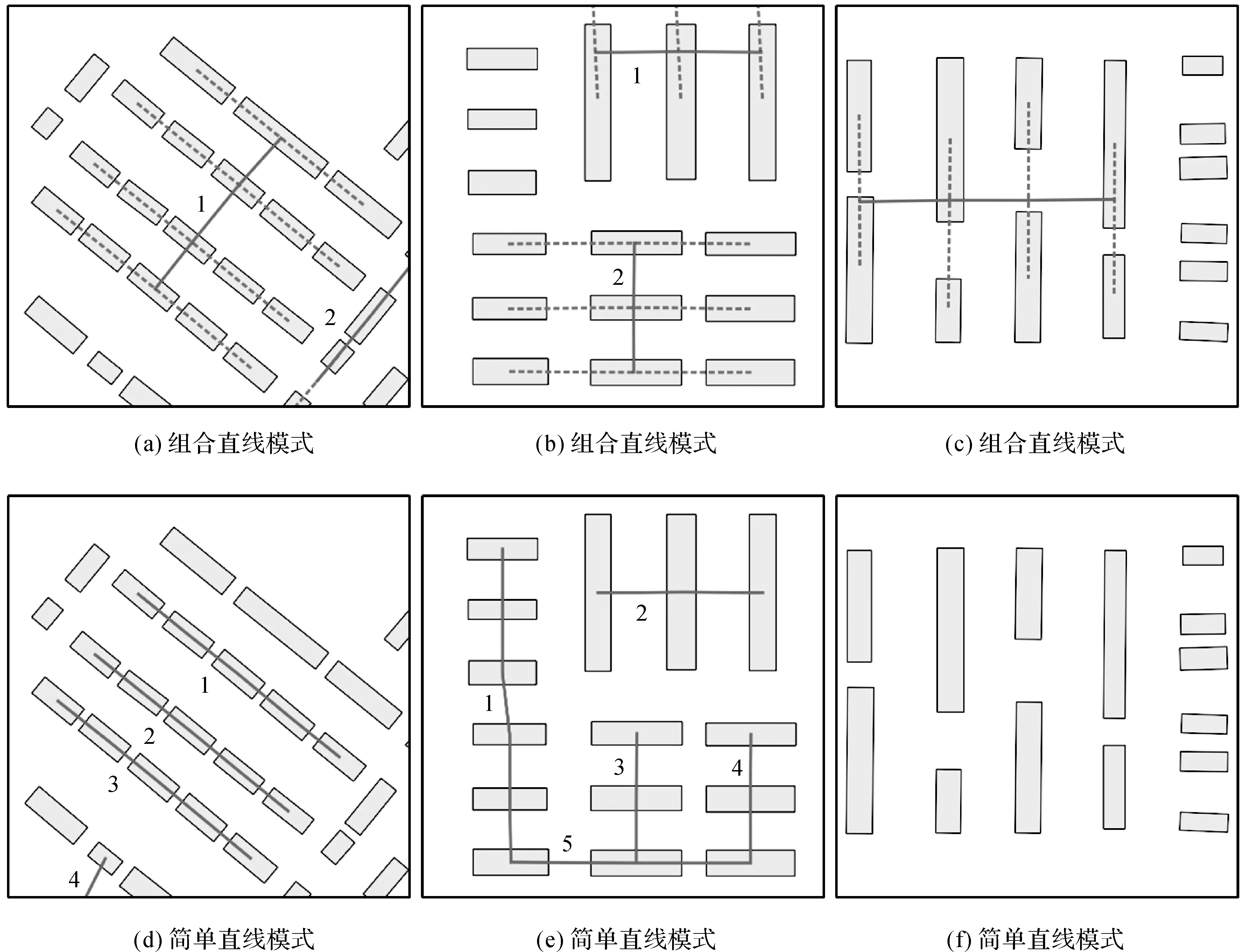
圖9 試驗結果細節對比Fig.9 Experiment result detail comparison

3.2 討 論

3.2.1 環境上下文約束

本文提取直線模式時未顧及環境上下文的約束，如道路網、水系等地理要素對城市空間形態的劃分，在實際應用(如制圖綜合、多尺度表達等)中可以根據實際需求，結合鄰域環境約束對提取的建筑群組合直線模式進行分解與重構。

3.2.2 建筑物及模式的可組合性

視知覺拓撲理論認為人的認知具有“大范圍首先”的性質[22-23]，這解釋了組合直線模式雖然在局部范圍內存在一定程度的異質性，但在整體上符合直線模式認知特征的現象，反映了模式在認知意義上的整體性、組合性和層次性。本文所提的組合直線模式重點關注模式內建筑物的可組合性，可組合性主要通過兩個條件判定，一是建筑物構成擴展對齊分布，二是建筑物之間具有一定的鄰近程度。本文在識別提取組合直線模式時并未對鄰近程度進行量化約束，因為鄰近程度的考量需要結合實際應用環境，本文所提方法主要從技術的角度為識別提取組合直線模式提供一個可行的數據增強方案。對本文試驗1中提取的組合直線模式內組合的建筑物間最短距離進行計算，統計結果如圖10所示，其中最小值為2.5 m，最大值為26.0 m。以制圖綜合為例，建筑物之間的最小間隔通常為0.5 mm[26]，如果綜合目標比例尺為1∶25 000，則實際距離約束為12.5 m，由圖10統計結果可知本文提取的組合直線模式中有61組組合建筑物符合鄰近程度的約束，如果試驗中加入距離約束條件Distance<12.5 m，則識別結果如圖11所示，共識別出12個組合直線模式。

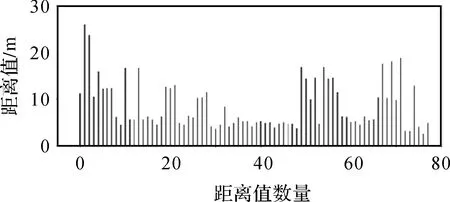
圖10 組合建筑物最短距離統計Fig.10 Statistics on minimum distance between combined buildings

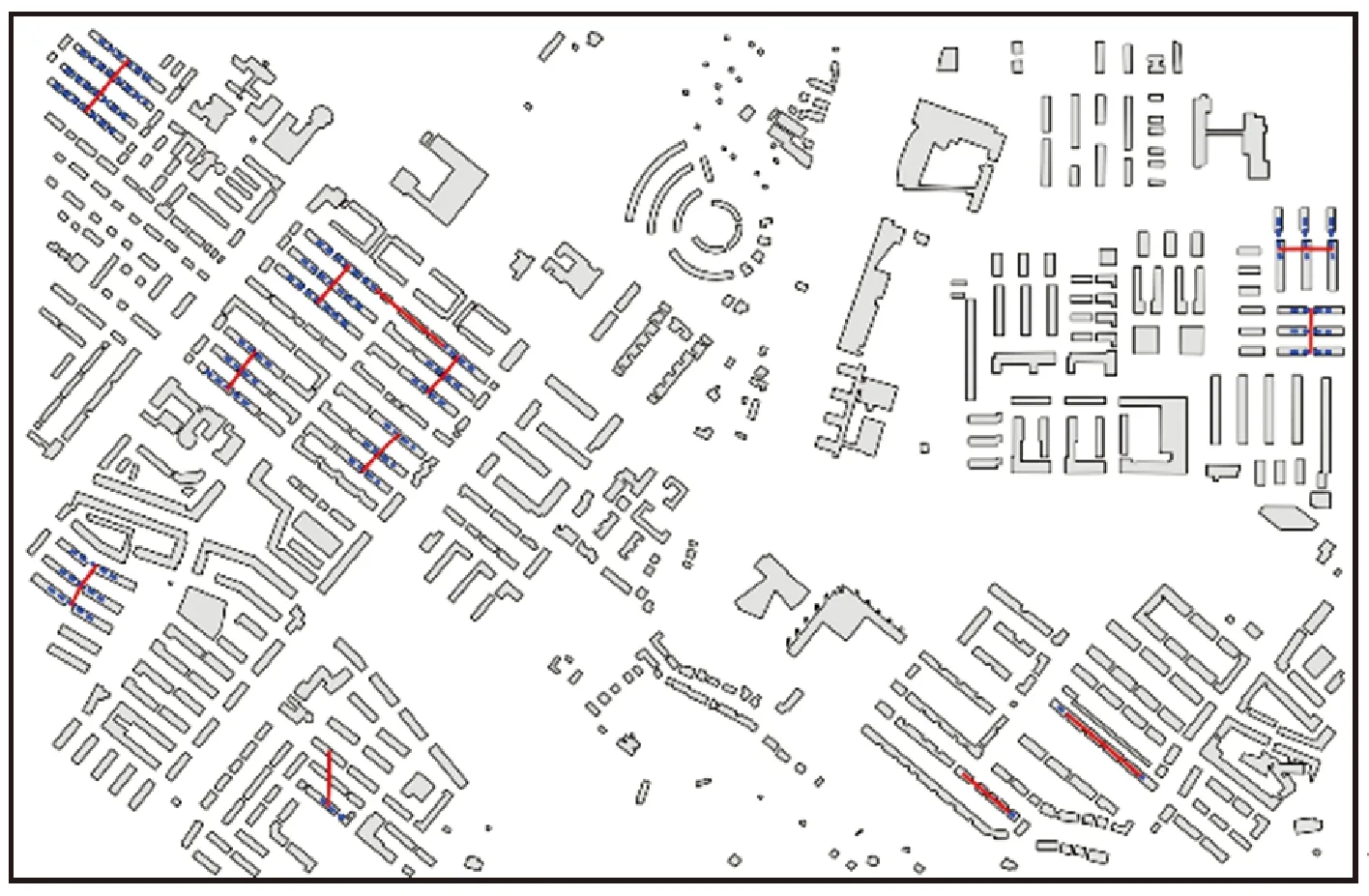
圖11 考慮距離約束的組合直線模式提取Fig.11 Combined collinear pattern extraction considering distance constraints

建筑物的可組合性也可以延伸為模式與模式之間的可組合性，如圖12(a)所示的組合直線模式完全由兩個鄰近且具有相似分布特征的簡單直線模式(圖12(b))組成。模式之間的可組合性對研究具有復雜組合形態和多層次性的直線模式具有重要的理論指導意義。

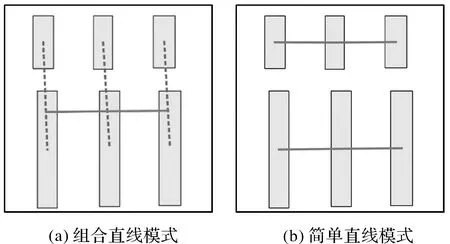
圖12 模式間的可組合性Fig.12 Combination of different patterns

3.2.3 參數閾值

(1) 參數相關性方面。本文模式識別過程涉及多個參數，各參數是相互獨立、互不影響的。首先，根據建筑物形狀、尺寸和方向建立的不同類型參數是互不影響的；其次，每個類型之內的參數是相互獨立、相互補充的。矩形度主要用來限定模式識別的對象為形狀規則的建筑群；模板放大系數主要是考慮到模板匹配方法缺失一定的靈活性，因此對模板適當放大以擴大搜索范圍，增大所提方法的靈活性；長度比和模板重合度雖然都涉及度量尺寸的大小，但模板重合度的主要作用是通過面要素的相交關系和程度確定符合要求的待匹配建筑物，長度比則主要通過度量建筑物間的大小差異來進一步匹配；對于局部方向差異和整體方向差異，局部方向差異是度量建筑物之間主方向差異的參數，反映了不同建筑物的方向相似性，整體方向差異是度量一個直線模式內建筑物的整體方向異質性，反映了整個模式的直線性，因此局部方向差異和整體方向差異是相互獨立的參數。雖然在擴展對齊聚類階段也采用了尺寸和方向方面的參數，但這些參數主要是用來確定作為模式構件的組合建筑物，而模式識別階段采用的參數主要用來確定構成直線模式的模式構件。因此，本文模式識別過程中所用到的參數都是必要的且相互獨立、互不影響。

(2) 參數閾值設置方面。閾值的設置主要以經驗值為主，同時結合試驗進行微調。基于大多數建筑物的規則性考慮以及組合直線模式對規則程度的依賴，本文在識別提取組合直線模式的過程中僅考慮矩形度較高的建筑物，在一定程度上損失了形狀信息。長軸、短軸長度比作為控制形狀、大小的參數，其閾值設置存在一定差異的原因是試驗數據中延伸率[11]高的建筑物占據多數，相較于短軸，長軸維度的信息屬于人類視覺感知認知過程中被優先傳遞的顯著性信息。因此，長軸長度比的約束規則更為嚴格，閾值更大。閾值的調整需結合模式形態的側重點，若僅考慮短軸長度比而忽略其他因素對組合直線模式的影響，如圖13(a)、(b)、(c)分別為短軸長度比閾值取0.75、0.8、0.85的試驗結果，對比發現隨著短軸長度比閾值的收緊，由于短軸長度較大的建筑物被剔除，導致模式的退化。

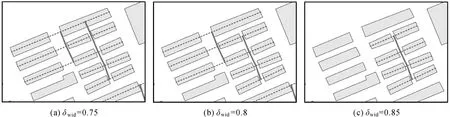
圖13 短軸長度比影響Fig.13 Influence of minor axis length ratio

(3) 參數對數據、尺度的適應性分析。對于不同類型的數據，由于空間分布情況不同，參數的閾值可能需要調整，但必須符合模式的認知特征。所以對于不同的數據，參數閾值不會發生太大的變化。例如3.1節兩組不同試驗數據的參數閾值雖不相同，但整體變化并不大(表2)。對于不同尺度的數據，空間分布模式在空間認知上有“建筑物微觀局部特征—街區形狀特征—城市整體分布特征”的層次性，參數和閾值主要由模式的類型決定，如直線型建筑群、條帶型街區和輻射型城市等。本文則主要研究微觀局部特征明顯的建筑物直線分布模式，結合3.1節不同尺度數據的試驗結果，本文的參數適用于大比例尺建筑群的組合直線模式識別。

3.2.4 評估識別結果的可靠性

視覺認知易受人類的個體差異性和主觀性的影響，因此對基于視知覺空間認知的模式識別結果的定量評價一直是該領域的難題。目前，通過與人眼識別的結果進行對比來評價識別結果是普遍被認可的方法[2,4,9,18-19]。本文通過問卷調查的方式評價結果的可靠性，調查對象為4名制圖生產單位工程師，6名助理工程師和30名地圖專業學生。分別對比3.1節兩組試驗數據的調查結果與所提方法的識別結果，以準確率和召回率對識別結果進行評價，評價結果見表3，結果表明本文方法的識別結果是可靠的。

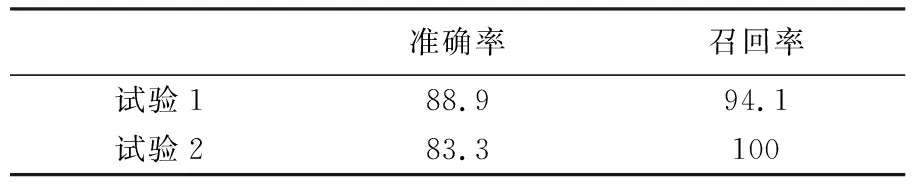
表3 識別結果評價

4 結 論

目前，建筑群直線模式的研究僅考慮了模式內建筑物間的同質性以及模式內、外建筑物間的異質性。本文針對具有局部異質性的建筑群直線模式識別問題，提出基于模板匹配的建筑群組合直線模式識別方法。本文旨在提供一個建筑群空間分布模式識別的技術方案，在識別提取組合直線模式過程中未考慮組合建筑物的空間鄰近程度和其他地理要素的約束，具體考慮的約束條件要結合實際需求，在以后的工作中會對此繼續研究。此外，會進一步分析不同數據特點對閾值設置的具體影響，以及對復雜組合形態和多層次性的直線模式進行研究。