基于KPCA-WOA-KELM的巖爆烈度預測

郭延華，趙 帥

(河北工程大學 土木工程學院，河北 邯鄲 056038)

巖爆是隧道開挖時，因巖體受到擾動，其中聚積的彈性能突然釋放，導致巖體脫落、爆裂、彈射的動力失穩現象，嚴重時可造成重大財產損失和人員傷亡[1]。隨著我國經濟的快速發展，對地下深部資源開采和地下工程建設的需求愈發強烈，對巖爆預測與防治的研究也愈發重要。

在巖爆烈度預測方面，國內外學者進行了大量的研究[2-3]，神經網絡[4]、功效系數法[5]、模糊數學[6]、灰色理論[7]、支持向量機[8]、數據挖掘[9]、PCA-PNN法[10]、PCA-OPF法[11]等數學模型與智能算法被提出。但上述預測方法一般基于少量巖爆案例的小樣本巖爆數據，而巖爆數據的數量與質量往往影響巖爆預測的準確性和可靠性[12]，所以由此建立的預測模型的可靠性與泛化性較差。此外上述方法的預設參數往往由人工經驗設置，預測結果受人主觀因素影響較大，或僅對巖爆數據作線性降維，未考慮數據間的非線性關系，從而未充分保留巖爆數據的特征信息。因此在巖爆預測方面需要進一步研究，并提出經濟可靠的巖爆預測方法。

核極限學習機(Kernel Based Extreme Learning Machine，KELM)是一種分類預測算法，該算法將核函數與極限學習機(Extreme Learning Machine，ELM)相結合，以提高ELM算法的預測性能。故本文巖爆烈度預測將基于KELM實現，同時為解決因人工設置參數而影響KELM預測效果的問題，使用鯨魚優化算法(Whale Optimization Algorithm，WOA)尋優KELM的懲罰系數C和核函數參數s以提高其預測性能。此外，考慮到巖爆評價指標之間的多維交叉冗余性，使用核主成分分析(Kernel Principal Component Analysis，KPCA)對巖爆數據集做特征壓縮，相比于傳統的主成分分析(Principal Component Analysis，PCA)，KPCA能對數據集做非線性降維，從而能更加充分地保留特征信息，以提高KELM的訓練速度和預測速度，故本文建立KPCA-WOA-KELM的巖爆烈度預測模型。

1 模型原理與建立

1.1 KPCA理論基礎

PCA是對數據做線性降維的傳統降維算法，而對具有非線性關系的數據做特征提取時，卻無法充分保留數據的特征信息。KPCA在其基礎上結合核函數，將數據映射至高維空間中做數據壓縮。KPCA能在充分保留數據特征信息的基礎上做數據壓縮[13]。

1.1.1 KPCA基礎理論

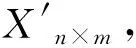
使用函數φ將樣本映射至高維特征空間RF，映射值為φ(x1)，φ(x2)，…，φ(xn)并使用PCA方法得到協方差矩陣為：

(1)

其特征方程為：

Cν=λν

(2)

式中，λ為協方差矩陣的特征值，ν為特征向量，由式(1)、式(2)可得ν：

(3)

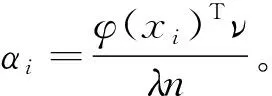
k(xi,xj)=φ(xi)Tφ(xj)

(4)

對于式(2)，任意的k=1，2，…，n，有：

φ(xk)Cν=λφ(xk)ν

(5)

分別將式(1)、式(3)與式(4)帶入式(5)可得：

Kα=λnα

(6)

式中，K為k對應的核矩陣，K=k(xi,xj)，α=(α1,α2,...,αn)。

通過式(6)，求得特征值λ1≥λ2≥…λn及其對應特征向量α1,α2,…,αn。選取p(p≤n)個特征值，滿足累計貢獻率≥85%。新樣本φ(xj)投影后的第j(j=1,2,…,p)維坐標為：

(7)

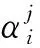
(8)

1.1.2 核函數的選擇

核函數的類別一般分為局部核函數和全局核函數，而核函數的選擇往往影響KPCA數據降維的效果。為更加充分地保留數據特征信息，本文將兩類核函數加權組合從而建立新的核函數。其中核函數參數通過多重實驗的方法得出，組合核函數比例系數采用網格搜索法選取最優組合系數，使其貢獻率達到最大值。核函數選用高斯核函數(局部核函數)和多項式核函數(全局核函數)：

(9)

k(x,x′)=(γ(x,x′)+c)d

(10)

式中，σ為高斯核函數的待定參數，γ、c、d為多項式核函數的待定參數。

將式(9)與式(10)加權組合得：

η2×(γ(x,x′)+c)d

(11)

式中，η1、η2為組合核函數的比例系數。

1.2 WOA理論基礎

WOA[14-15]是受座頭鯨捕食行為的啟發而提出的一種群智能算法。座頭鯨在發現獵物后，會下潛并旋繞，對獵物進行泡泡網攻擊，如圖1所示。該過程主要經歷三個階段：隨機捕獵、環繞獵物以及捕食獵物。

圖1 座頭鯨泡泡網攻擊捕獵行為示意Fig.1 Humpback whale bubble net attack and hunting behavior

1.2.1 隨機捕獵

模擬鯨魚群隨機捕獵的方式求可行解，數學模型如下：

D=|C·X*(t)-X(t)|

(12)

X(t+1)=X*(t)-A·D

(13)

式中，X*為當前最優位置向量，t為當前迭代數，D為位置衡量參數，X為位置向量，A和C為控制參數向量，可通過下式計算：

A=2a·r-a

(14)

C=2·r

(15)

(16)

式中：r為任意向量，tMaxlter為最大迭代數，a隨迭代次數的增加由2減少至0，從而實現收縮環繞機制。

1.2.2 環繞獵物

環繞更新位置通過螺旋方程來表示：

D′=|X*(t)-X(t)|

(17)

X(t+1)=D′·ebl·cos(2πl)+X*(t)

(18)

式中：D′為最佳位置距當前位置的距離，l為[-1,-2]中任意數；b為對數螺旋形狀的常數，通過公式(19)計算。

(19)

求解時收縮環繞和螺旋更新同時進行，各賦予兩種方式1/2的概率執行：

(20)

式中：p為[0,1]的隨機數。

1.2.3 捕食獵物

探索過程中，通過全局搜索更新最佳位置以達到最優，數學描述為：

D=|C·Xrand-X|

(21)

X(t+1)=Xrand-A·D

(22)

式中：Xrand是當前一代中的隨機位置向量。其中|A|<1時，使用收縮環繞局部尋優；|A|≥1時，使用探索全局尋優。

1.3 KELM理論基礎

ELM[16]是一種單隱含層前饋神經網絡，其學習目標函數F(x)可用矩陣表示為：

F(x)=h(x)×β=H×β=L

(23)

β=H*·L

(24)

式中：x為輸入向量，h(x)、H為隱層節點輸出，β為輸出權重，L為期望輸出H*為H的廣義逆矩陣。

引入懲罰系數C和單位矩陣I增強神經網絡的穩定性，則輸出權值的最小二乘解為：

(25)

引入核函數到ELM中，核矩陣為：

ΩELM=HHT=h(xi)h(xj)=K(xi,xj)

(26)

式中：xi，xj為試驗輸入向量，則可將式(23)表達為：

(27)

式中：(x1,x2…,xn)為給定訓練樣本，n為樣本數量。核函數選用高斯核函數即：

(28)

懲罰系數C和核函數參數s的設置在一定程度上影響KELM[17]的預測性能。

1.4 KPCA-WOA-KELM模型構建

本文巖爆案例基于Zhou等收集的國內外地下工程和礦山中245組巖爆案例[18]。去除部分埋深數據缺失案例后，選取巖爆烈度判別指標并隨機將數據集分為訓練集174例與測試集30例。

首先利用KPCA對巖爆數據做特征提取，然后將訓練集輸入KELM進行訓練，并使用WOA對其參數優化，最后利用測試集測試該預測模型的準確性。基于KPCA-WOA-KELM的巖爆烈度預測模型的流程如圖2所示：

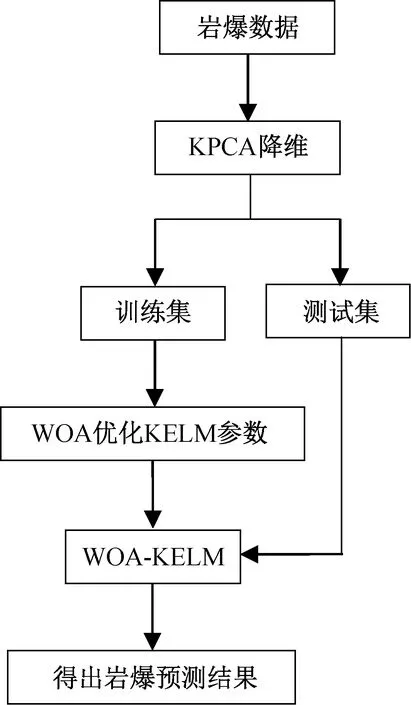
圖2 巖爆烈度預測模型流程Fig.2 The process of rockburst intensity prediction model

2 巖爆烈度仿真實驗與分析

2.1 巖爆烈度預測指標選取

影響巖爆的因素具有顯著的突發性、隨機性與復雜性的特點，其主要包括巖性、地質條件、開挖方式、圍巖初始應力狀態、隧道斷面型式等。

目前國內外學者對巖爆預測指標的選取通常基于巖石力學參數或巖爆判據。一般來說，選取巖爆預測指標應符合易于獲取、代表性與可操作性強的特點，能從多個方面反映巖爆的特征信息。

根據巖爆的影響因素、特點及成因，本文選取巖爆埋深D，圍巖最大切應力σθ，單軸抗壓強度σc，單軸抗拉強度σt，應力集中系數SCF(最大切向應力比單軸抗壓強度)，脆性系數(單軸抗壓強度比單軸抗拉強度B1和單軸抗壓、抗拉強度之差與兩者之和的比值B2)，彈性能量指數Wet作為巖爆烈度的主要評判指標。將巖爆分為4級：無巖爆、輕微巖爆、中等巖爆、強烈巖爆，其級別分別對應Ⅰ級、Ⅱ級、Ⅲ級、Ⅳ級，表1為不同理論判據下巖爆烈度分類標準表[19]。

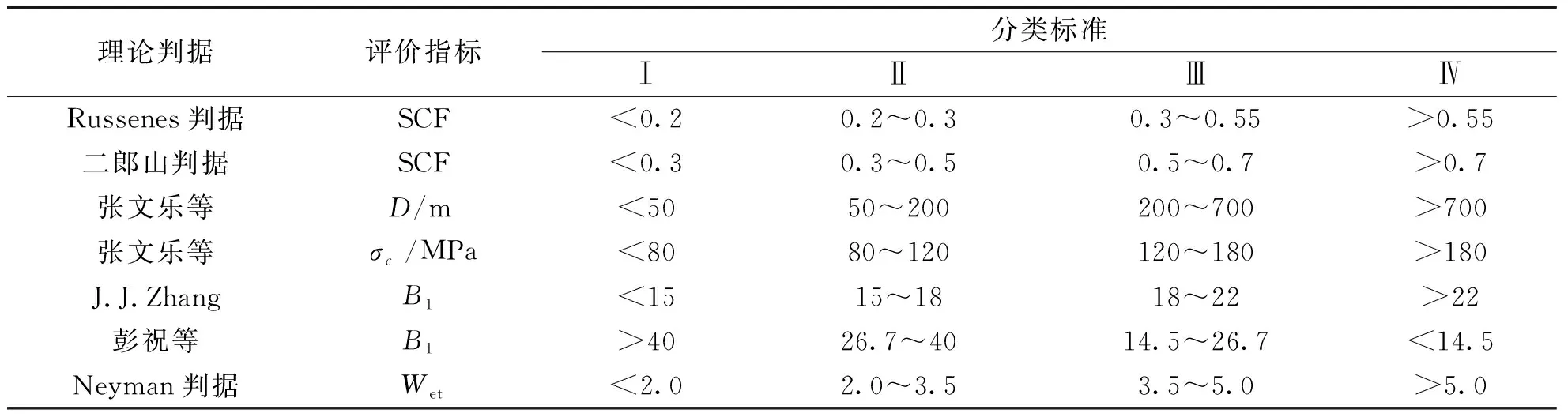
表1 不同理論判據的巖爆烈度分類標準

2.2 KPCA特征提取

KPCA特征提取步驟為：

(1)選取巖爆數據。

(2)歸一化初始數據矩陣。

(3)使用核技巧將樣本空間映射至高維空間構建核矩陣Kn×n。

(4)核矩陣中心化，即：

(29)

其中，In為元素均為1/n的矩陣。

(5)求解核矩陣的特征值λ，排序特征向量α。選取出p(p≤n)個特征向量，并根據式(8)規范化。

(6)通過特征值和特征向量得出主成分，樣本xj在特征向量αk上的投影為：

k=1,2,…,p

(30)

構造特征提取后的矩陣Rn×p。

分別通過組合核函數、高斯核函數和多項式核函數實現KPCA特征提取，其中高斯核函數參數σ=1.81，多項式核函數中d=3，γ=c=1，組合系數η1=0.7，η2=0.3。

表2為通過不同核函數分別得到的特征值，貢獻率和累計貢獻率。可以看出，組合核KPCA得到70.43%的第一主成分貢獻率，遠大于高斯核、多項式核KPCA，說明相比于單一核KPCA，組合核KPCA具有更好的特征提取能力。

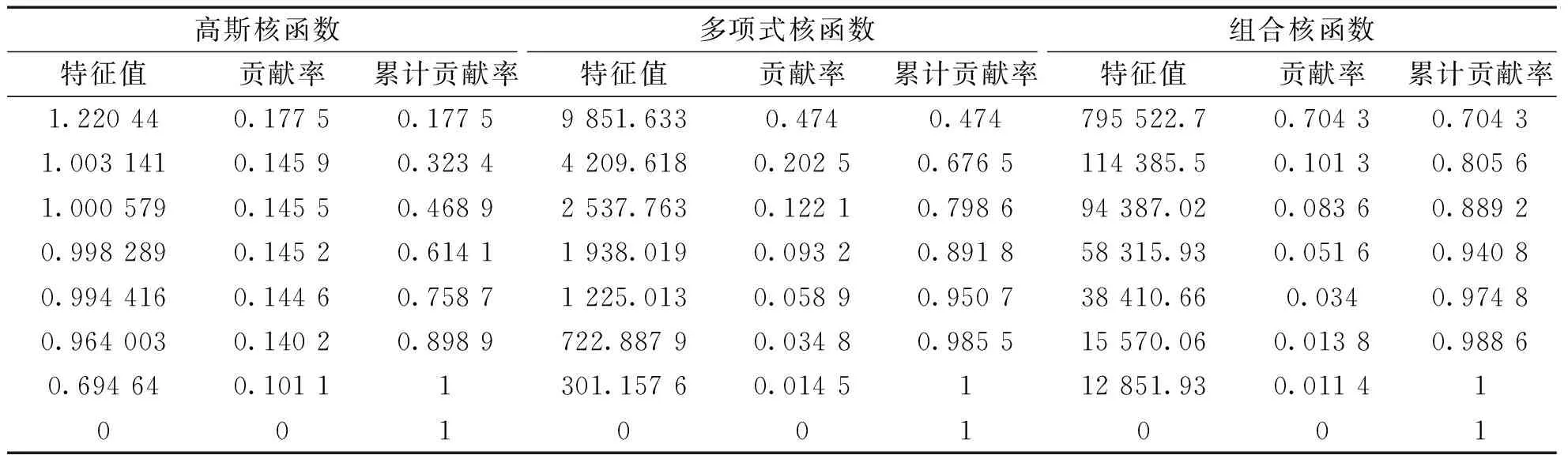
表2 不同核函數特征提取結果對比

2.3 WOA優化KELM模型

由于KELM對其核函數參數的敏感性，直接使用KELM建模，往往導致預測結果產生較大誤差。因此，為提高KELM的預測性能，使用WOA算法對KELM的懲罰系數C和核函數參數s進行全局尋優。具體步驟如下：

(1)歸一化KPCA降維后的數據集。

(2)參數設置：變量數dim=2、鯨魚數量SearchAgents_no=30、最大迭代次數tMaxlter=150，變量下限lb=[30,0.2]，變量上限ub=[500,0.7]。

(3)種群初始化：令n=SearchAgents_no，鯨魚位置為：

(31)

通過下式計算鯨魚初始隨機種群位置X0，迭代數t=1：

X0(i,j)=(ub(i)-lb(i))×rand(i,j)+lb(i)

(32)

式中：X0(i,j)為式(31)第i行第j列的值，lb(i)和ub(i)為第i個座頭鯨的下限和上限，rand(i,j)為[0,1]內的隨機數。

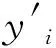
(5)利用WOA尋優得到最優Cbest和sbest如表3所示。

表3 不同核KPCA下KELM最優參數

(6)將Cbest和sbest代入KELM得到KPCA-WOA-KELM的巖爆烈度等級預測模型。

2.4 KPCA-WOA-KELM模型實測

將30例測試數據輸入模型中，結果如圖3所示。

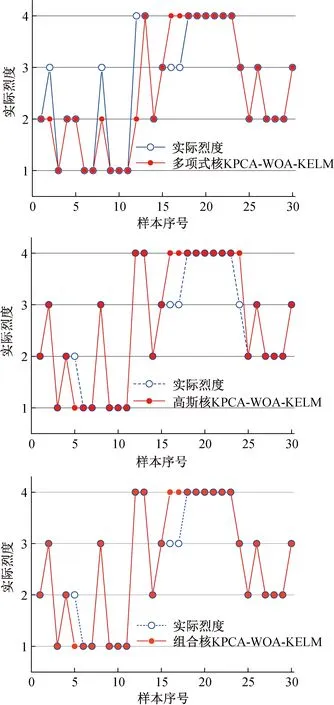
圖3 不同核KPCA-WOA-KELM巖爆烈度預測結果Fig.3 KPCA-WOA-KELM rockburst intensity prediction results for different core

該模型相關評估指標如表4所示。分別采用F值、準確率(Accuracy)、精確率(Precision)、召回率(Rcall)量化KPCA-WOA-KELM的預測性能。其中Accuracy可量化模型整體的預測性能，其余指標則反映模型對4類巖爆等級中單獨的某一級的預測能力。

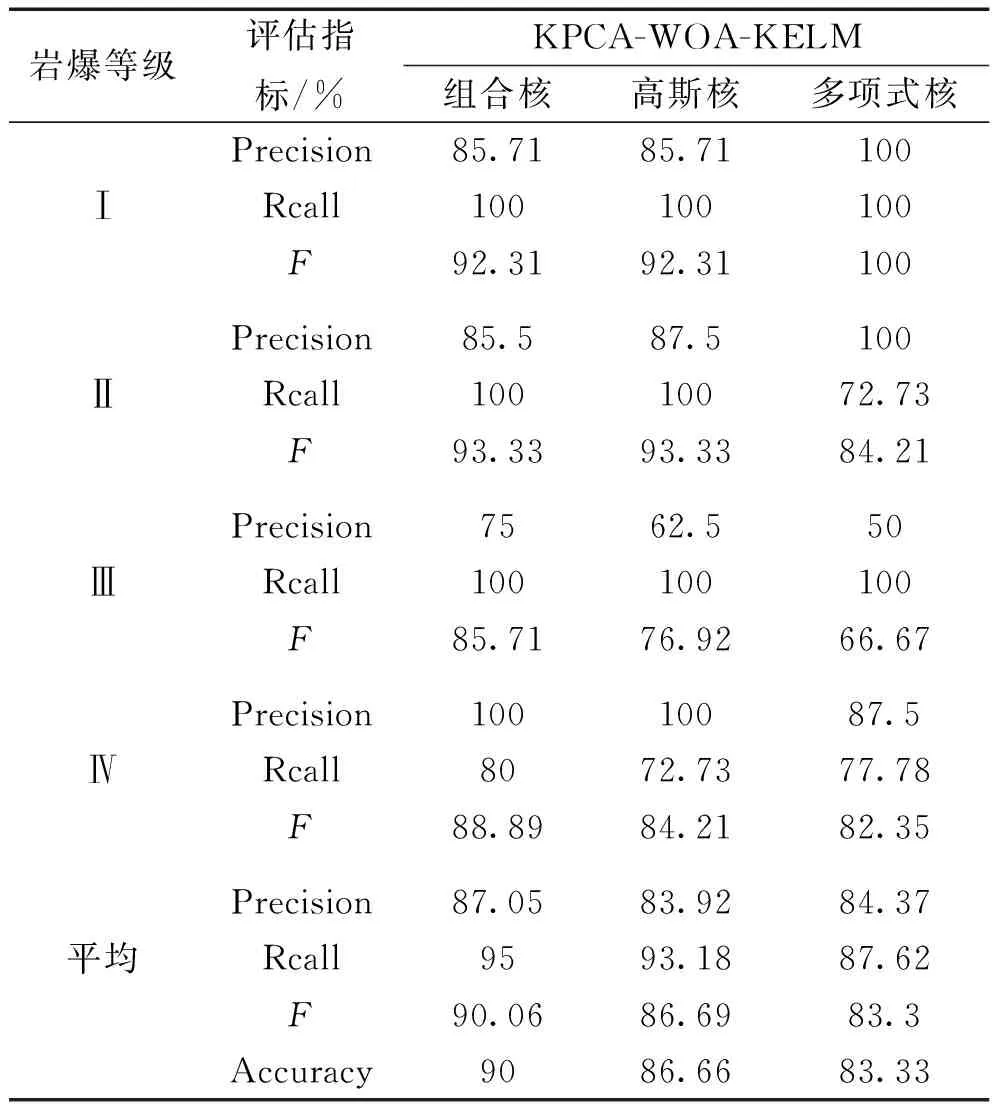
表4 不同核KPCA-WOA-KELM性能評價

組合核、高斯核和多項式核的KPCA-WOA-KELM的準確率分別為90%、86.66%、83.33%，精確率分別為87.05%、83.92%、84.37%，召回率分別為95%、93.18%、87.62%，F值分別為90.06%、86.69%、83.3%，說明該模型有較高的預測性能。其中，組合核KPCA-WOA-KELM預測能力最優，對4類巖爆等級分類精確率分別為85.71%～100%，85.71%～100%，87.5%～100%，召回率分別為80%～100%，72.73%～100%，72.73%～100%，F值分別為85.71%～93.33%，76.92%～93.33%，66.67%～100%。其中Ⅰ級巖爆與Ⅱ級巖爆的F值均大于Ⅲ級巖爆與Ⅳ級巖爆的F值，說明該模型對Ⅰ級巖爆與Ⅱ級巖爆的預測性能較強，而對于Ⅲ級巖爆與Ⅳ級巖爆的預測性能較弱。

綜上所述，綜合考慮該模型的準確率及相關評價指標，組合核KPCA-WOA-KELM具有較好的預測性能。

3 工程實踐

3.1 工程概況

秦嶺終南山公路隧道全程18.02 km，最大縱坡11%。該工程采用雙洞雙線設計，凈寬10.5 m、限高5 m，安全等級一級，結構設計基準期100 a。該隧道深埋地段的最大水平主應力達到21.04 MPa，地應力水平較高，巖爆發生概率較大[20]。

3.2 模型應用

將KPCA-WOA-KELM模型應用于秦嶺終南山隧道工程巖爆烈度的預測。該工程巖爆相關指標如表5所示，預測結果與實際情況基本一致。表明KPCA-WOA-KELM在實際工程中有一定的可靠性，為實際工程提供一定的參考價值。

表5 終南山隧道巖爆實測數據與預測結果

4 結論

1)在確定巖爆烈度主要評判指標后，使用KPCA對巖爆數據做非線性降維，相比于PCA,KPCA能更充分保留特征信息，簡化KELM模型的輸入參數，同時借助WOA優化KELM的懲罰系數C和核函數參數s使其達到最優，從而提高模型的訓練速度與預測精度。

2)對局部核函數和全局核函數采用加權方式構造組合核KPCA，并與WOA優化的KELM相結合，建立組合核KPCA-WOA-KELM模型。使用204例巖爆案例對模型進行訓練與測試，并用準確率、精確率、召回率、F值等指標綜合評價KPCA-WOA-KELM的預測性能。結果表明，組合核KPCA-WOA-KELM相較于單一核KPCA-WOA-KELM有更高的預測性能。

3)為檢驗該模型的預測性能，將其應用于終南山公路隧道中對巖爆等級進行預測，結果表明與實際巖爆等級基本一致，說明該模型具有一定的工程應用價值。