密實(shí)度對粗粒料力學(xué)特性影響三軸試驗(yàn)研究

朱材峰，朱俊高*，潘 政

(1. 河海大學(xué) 巖土力學(xué)與堤壩工程教育部重點(diǎn)實(shí)驗(yàn)室，江蘇 南京 210098；2. 四川電力設(shè)計(jì)咨詢有限責(zé)任公司，四川 成都 610016)

粗粒料粒徑范圍廣，排列方式復(fù)雜，存在顆粒破碎效應(yīng)及剪脹效應(yīng)，具有極為復(fù)雜的力學(xué)性質(zhì)[1]。影響粗粒料力學(xué)性質(zhì)的因素有很多，比如相對密實(shí)度、顆粒級配、應(yīng)力歷史、加載條件、應(yīng)力路徑等，其中相對密實(shí)度是重要因素之一。密實(shí)度同時也是土石壩等填方工程設(shè)計(jì)時重要控制指標(biāo)之一，選取不當(dāng)會影響工程的經(jīng)濟(jì)性及安全性，所以探討相對密實(shí)度與土體力學(xué)性質(zhì)之間的關(guān)系是非常必要的。

姜景山等[2]利用大型真三軸試驗(yàn)得出密度和圍壓是影響粗粒土力學(xué)性質(zhì)的重要因素；徐日慶等[3]針對兩種級配不同的福建標(biāo)準(zhǔn)干砂，著重探討了不同初始相對密實(shí)度對砂土抗剪強(qiáng)度的影響；李振等[4]通過對同一級配的河床砂卵石在不同相對密度下進(jìn)行直接剪切試驗(yàn)得出：抗剪強(qiáng)度參數(shù)隨著干密度的增大而增大，最終有趨于某一穩(wěn)定值的趨勢；陳鋮等[5]采用三維顆粒流軟件PFC3D模擬研究了5種不同級配下粗粒土在3種不同圍壓下的變形特性；凌華等[6]通過大型三軸排水剪切試驗(yàn)研究了級配對粗粒土強(qiáng)度、變形、剪脹特性和顆粒破碎的影響，試驗(yàn)結(jié)果表明細(xì)顆粒含量的大小、是否含泥是粗粒土力學(xué)特性的重要影響因素；姜景山等[7]通過大型三軸壓縮試驗(yàn)得出密度是決定粗粒土初始彈性模量的根本因素, 而剪切變形過程中彈性模量則是密度和應(yīng)力狀態(tài)共同決定的；王俊杰等[8]通過室內(nèi)試驗(yàn)研究發(fā)現(xiàn)粗粒土的滲透系數(shù)隨著密實(shí)度的增加而逐漸減小。雖然前人已經(jīng)研究了相對密實(shí)度對土體力學(xué)性質(zhì)的影響，但是對粗粒料相關(guān)方面的研究不夠系統(tǒng)全面。

因此，本文基于前人的研究經(jīng)驗(yàn)[9-12]，通過對某大壩粗粒料進(jìn)行不同相對密實(shí)度下的常規(guī)三軸試驗(yàn)，探究不同相對密實(shí)度對粗粒料應(yīng)力應(yīng)變特性和強(qiáng)度特性的影響，為土石壩工程實(shí)踐提供一定的借鑒。

1 試驗(yàn)土料與試驗(yàn)方案

1.1 試驗(yàn)土料

本次試驗(yàn)土料選用某大壩地基覆蓋層料(為砂卵礫石料)，屬于無粘性粗粒料。由篩分試驗(yàn)可知覆蓋層料最大粒徑為100 mm，而常規(guī)中型三軸儀容許試樣最大粒徑為20 mm，故通過等量替代法[13-14]對原土料進(jìn)行縮尺得到試驗(yàn)替代料級配，原級配和試驗(yàn)替代料的級配曲線如圖1所示。采用震動臺法測得試驗(yàn)土料的最大干密度為2.30 g/cm3，由松填法測得試驗(yàn)土料的最小干密度為1.93 g/cm3。

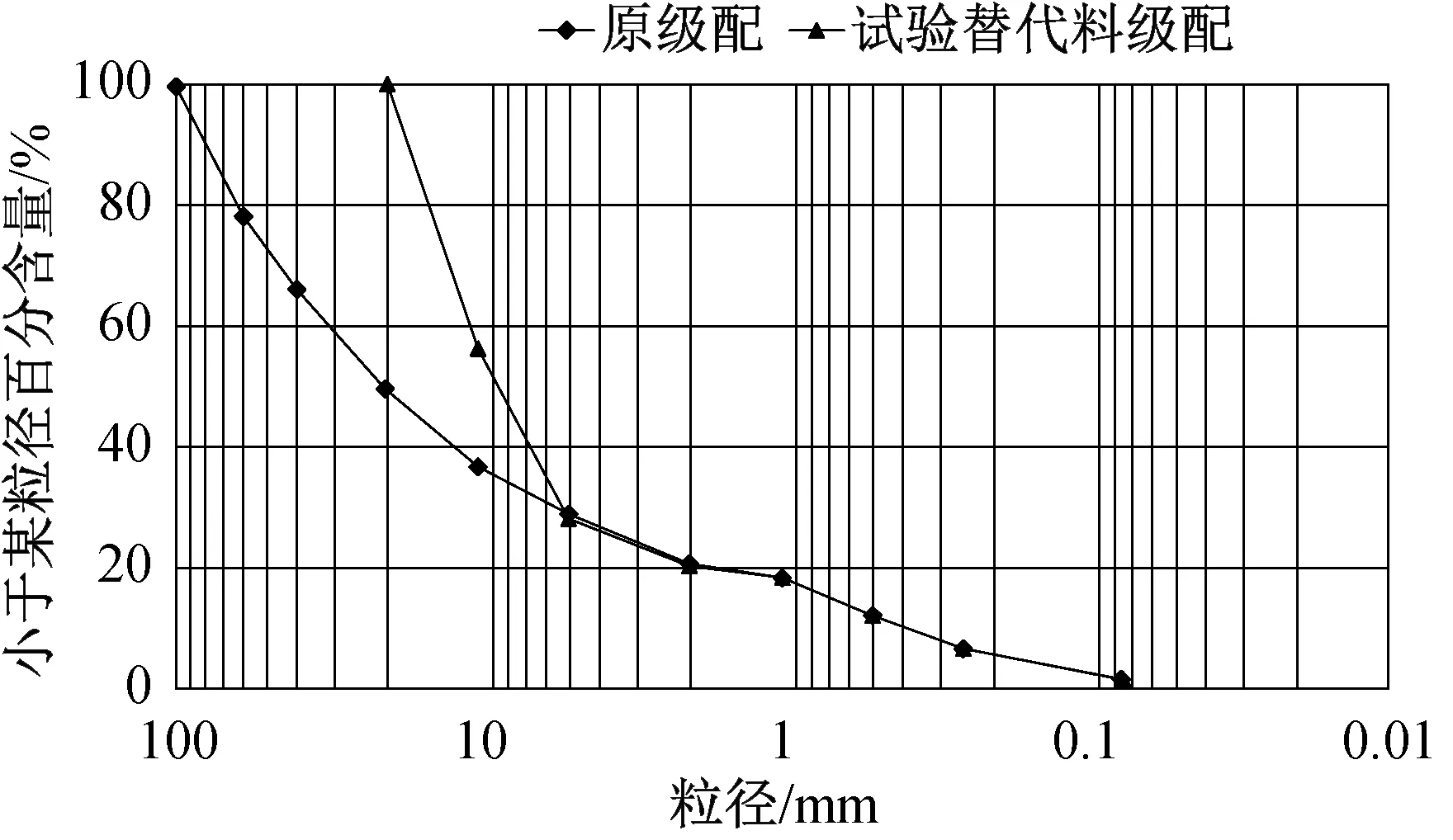
圖1 原土料和試驗(yàn)替代料的級配曲線Fig.1 Gradation graph of original soil material and test substitute

1.2 試驗(yàn)方案

本文試驗(yàn)在中型三軸儀(圖2(a))上進(jìn)行，試樣直徑為101 mm，高為200 mm。試驗(yàn)為固結(jié)排水剪(CD)，試樣的相對密實(shí)度Dr設(shè)計(jì)為0.7、0.8、0.9。每種相對密實(shí)度制備4個試樣，制樣時按等量替代法縮尺的級配比例算出每個粒徑范圍內(nèi)所需要的粗粒料的質(zhì)量，然后分5層擊實(shí)，固結(jié)時間為1 h，受剪前試樣如圖2(b)所示。對同一相對密實(shí)度下的4個試樣分別施加200、400、800、1 200 kPa的圍壓。

圖2 試驗(yàn)儀器和試樣Fig.2 Test equipment and samples

對于本文試驗(yàn)所用的無粘性粗粒料來說，剪切過程中孔隙水壓力易消散，抗剪強(qiáng)度基本不受剪切速率的影響，故剪切速率取0.25 mm/min，剪切至30 mm終止。

2 試驗(yàn)結(jié)果分析

2.1 應(yīng)力應(yīng)變特性分析

試驗(yàn)結(jié)束后的受剪試樣如圖3所示，圖4至圖7給出了不同圍壓下不同相對密實(shí)度的應(yīng)力應(yīng)變關(guān)系曲線，由圖可得：試樣的應(yīng)力應(yīng)變曲線均表現(xiàn)為軟化型，對于相對密度為0.7的試樣，在受剪初期，隨軸向應(yīng)變的增加，應(yīng)力逐漸上升到峰值后開始緩慢降低，在受剪后期，曲線出現(xiàn)水平段，應(yīng)力趨于一恒定值，通常將這一恒定的強(qiáng)度稱為殘余強(qiáng)度，這與密實(shí)砂土所表現(xiàn)出來的應(yīng)力應(yīng)變特性很相似[15]。對于相對密實(shí)度為0.8、0.9的試樣，應(yīng)力達(dá)到峰值后，應(yīng)力大小并沒有立即下降，而是出現(xiàn)長度不等的水平段，應(yīng)力值變化在5%以內(nèi)，此時試樣仍具有較大的強(qiáng)度，特別在高圍壓時表現(xiàn)得較為明顯。

圖3 受剪后試樣Fig.3 Sample after shearing

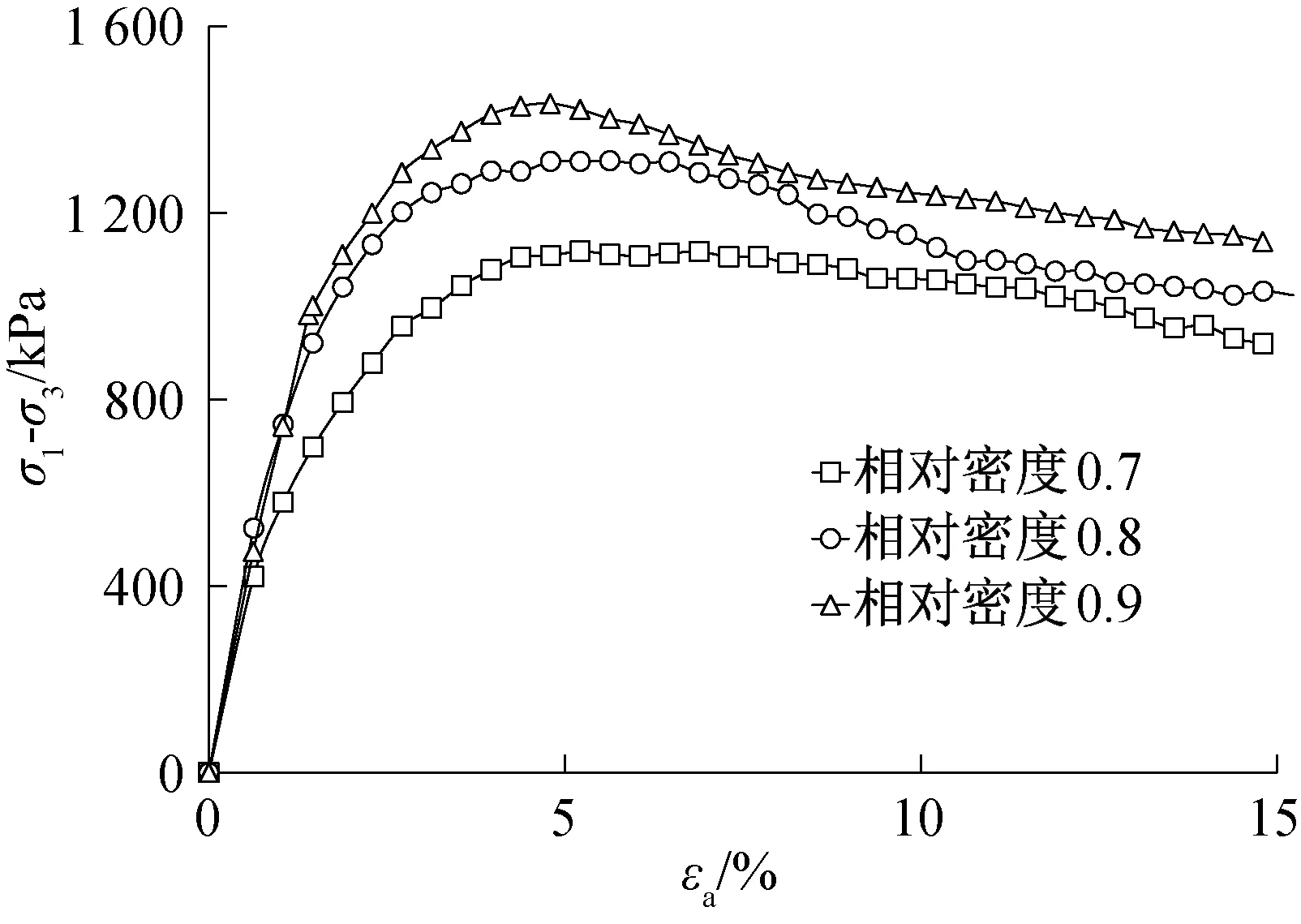
圖4 200 kPa圍壓下不同相對密實(shí)度(σ1-σ3)-εa關(guān)系曲線Fig.4 (σ1-σ3)-εa curves of different relative density under 200 kPa confining pressure

圖5 400 kPa圍壓下不同相對密實(shí)度(σ1-σ3)-εa關(guān)系曲線Fig.5 (σ1-σ3)-εa curves of different relative density under 400 kPa confining pressure

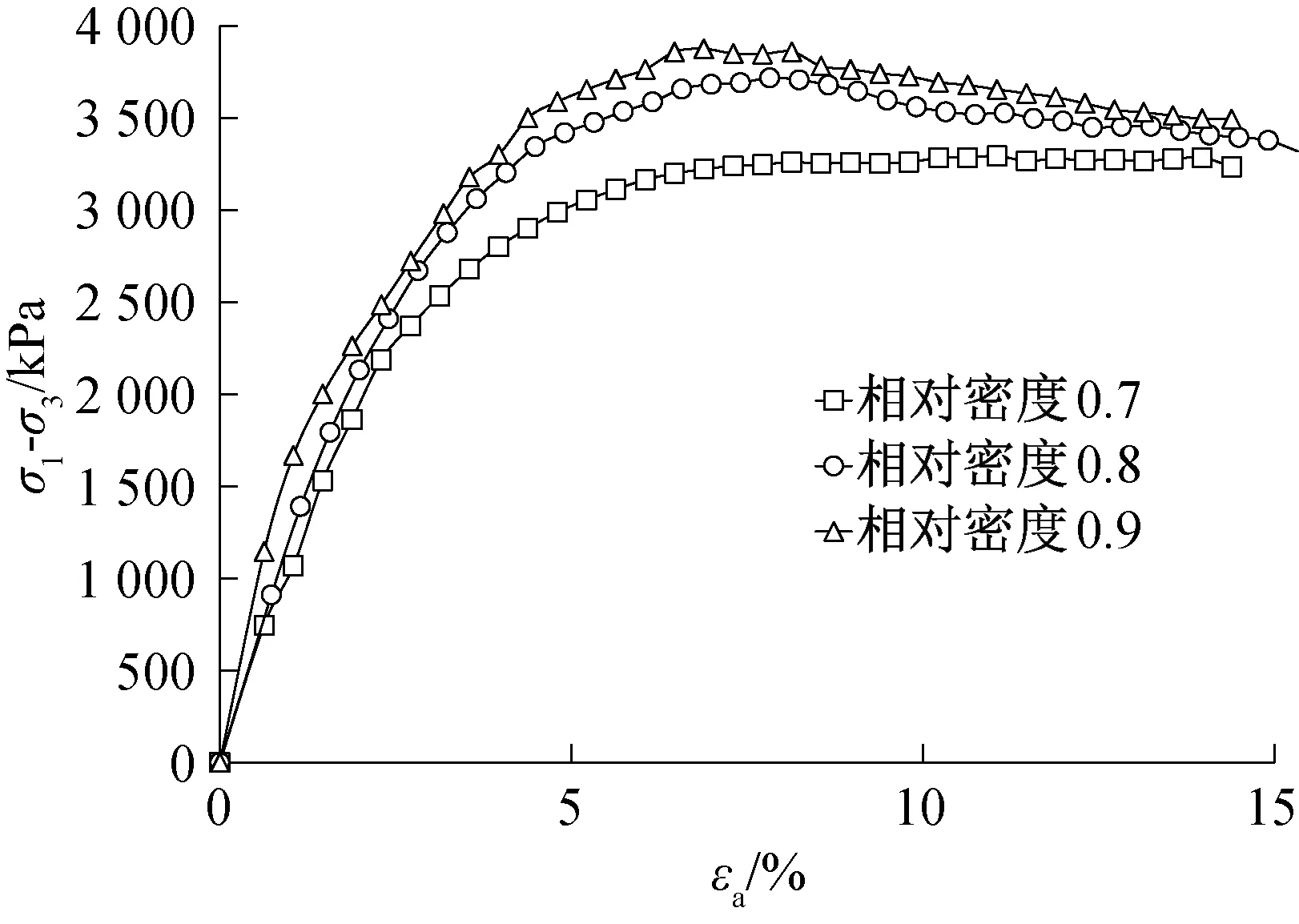
圖6 800 kPa圍壓下不同相對密實(shí)度(σ1-σ3)-εa關(guān)系曲線Fig.6 (σ1-σ3)-εa curves of different relative density under 800 kPa confining pressure

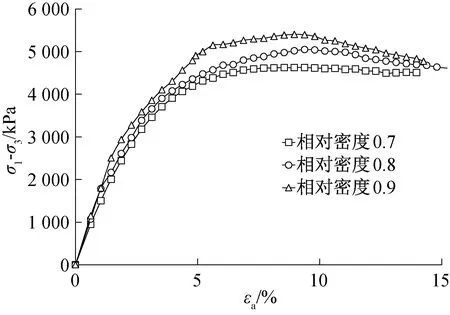
圖7 1 200 kPa圍壓下不同相對密實(shí)度(σ1-σ3)-εa關(guān)系曲線Fig.7 (σ1-σ3)-εa curves of different relative density under 1 200 kPa confining pressure

之所以出現(xiàn)上述現(xiàn)象，是由于當(dāng)制樣密度較大，圍壓較大時，在受剪初始階段，顆粒間接觸緊密，剪力較小，不足以引起顆粒破碎以及顆粒間的相對移動，變形以彈性為主，隨著剪力的不斷增加，當(dāng)剪力大于顆粒間接觸力時，一部分顆粒有滾過其他顆粒而產(chǎn)生相對錯動的趨勢，此時必須要克服較大的咬合作用力，所以表現(xiàn)出較高的抗剪強(qiáng)度；而且當(dāng)剪力超過顆粒本身強(qiáng)度時，顆粒間點(diǎn)接觸的尖角部位發(fā)生斷裂破碎，產(chǎn)生了細(xì)顆粒，進(jìn)一步充填了原來的孔隙，使得結(jié)構(gòu)更加緊密，因此仍然能夠承擔(dān)較大的剪力。

試樣在不同相對密實(shí)度不同圍壓下的峰值強(qiáng)度如表1所示，從表1可以看出同一相對密實(shí)度下試樣所受的圍壓越大，所表現(xiàn)出的峰值強(qiáng)度就越大，峰值強(qiáng)度越遲出現(xiàn)；同一圍壓下，試樣的相對密實(shí)度越大，所表現(xiàn)出的峰值強(qiáng)度也越大，峰值強(qiáng)度越早到達(dá)。

表1 不同相對密實(shí)度不同圍壓下的峰值強(qiáng)度(單位：kPa)

這是由于相對密實(shí)度大的試樣，顆粒之間填充密實(shí)，剪切初期，顆粒之間沒有相互移動，一部分顆粒要滾過另一部分顆粒才能產(chǎn)生較大錯動，而相對密實(shí)度小的試樣，顆粒之間本身處于松散狀態(tài)，剪切初期顆粒之間的密實(shí)程度不斷提高，所以，在相同的圍壓下相對密實(shí)度大的試樣更早達(dá)到峰值強(qiáng)度，而相對密實(shí)度小的試樣有一段時間是處于顆粒重新排列變密實(shí)的過程，峰值強(qiáng)度會出現(xiàn)的晚一些。

由圖4至圖7還可以看出：在同一圍壓下，相對密實(shí)度對應(yīng)力應(yīng)變曲線的形態(tài)影響較大，在達(dá)到峰值強(qiáng)度以前，應(yīng)力應(yīng)變曲線形態(tài)均隨相對密實(shí)度的增加而變“陡”，即曲線初始斜率變大，初始切線模量Ei增大；在達(dá)到峰值強(qiáng)度以后，曲線表現(xiàn)出更加明顯的軟化現(xiàn)象。

Janbu[16]的研究發(fā)現(xiàn)，對于土體而言，初始切線模量Ei與圍壓近似表現(xiàn)出冪函數(shù)關(guān)系，具體可以表示為：

(1)

式中K和n為鄧肯-張模型參數(shù)，pa為大氣壓力，依此關(guān)系求得不同相對密實(shí)度下鄧肯-張模型參數(shù)Rf、n和K的值，如表2所示。

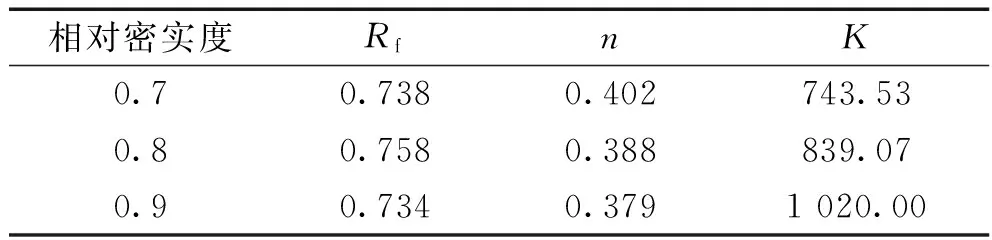
表2 不同相對密實(shí)度下鄧肯-張模型參數(shù)Rf、n和K

由表2可得，隨相對密實(shí)度的增大，參數(shù)Rf和n均僅在0.03左右內(nèi)波動，幾乎不受相對密實(shí)度的影響，如圖8(a)所示；參數(shù)K與相對密實(shí)度之間呈現(xiàn)出較好的線性關(guān)系，如圖8(b)所示，所以，參數(shù)K隨密實(shí)度Dr的變化可以近似用下式表示：

K=a1Dr+d1

(2)

式中，參數(shù)a1、b1分別為1 980.7、-747.2。

圖8 鄧肯-張模型參數(shù)與相對密實(shí)度Dr關(guān)系Fig.8 Relationship curves between Duncan Chang model parameters and Dr

應(yīng)變軟化是粗粒料的一個重要特性。軟化程度除了與顆粒自身巖性有關(guān)外，主要與密實(shí)程度和圍壓有關(guān)。要在本構(gòu)模型中準(zhǔn)確反映粗粒料的軟化特性，必須對其軟化規(guī)律有清楚的了解[17]。為此，作者對本文試驗(yàn)粗粒料的軟化性質(zhì)進(jìn)行了深入研究。

為了表示應(yīng)力應(yīng)變曲線的軟化現(xiàn)象，現(xiàn)引入?yún)?shù)λ，定義為粗粒料應(yīng)力應(yīng)變曲線的軟化系數(shù)，軟化系數(shù)λ由式(3)求得：

(3)

式中(σ1-σ3)f為峰值強(qiáng)度如表1所示，(σ1-σ3)r為殘余偏應(yīng)力如表3所示。

繪制出軟化系數(shù)λ和lg (σ3/pa)的關(guān)系曲線如圖9(a)所示，圖9(a)顯示，同一Dr對應(yīng)不同lg (σ3/pa)的4個點(diǎn)可近似用直線擬合，設(shè)λ-lg (σ3/pa)擬合直線的斜率和截距分別為α和ψ，整理發(fā)現(xiàn)，不同Dr時的斜率α相差不大，截距ψ隨相對密實(shí)度Dr變化也表現(xiàn)出比較好的線性關(guān)系，如圖9(b)所示。遂對斜率α取平均值為-1.27，利用α和ψ-Dr的關(guān)系來進(jìn)行直線擬合。可以得出，參數(shù)λ隨著圍壓σ3和密實(shí)度Dr的變化可以用式(4)表示：

(4)

式中α，β，δ為擬合參數(shù)，對于試驗(yàn)所用的粗粒料，分別等于-1.27，2.50，-0.42。

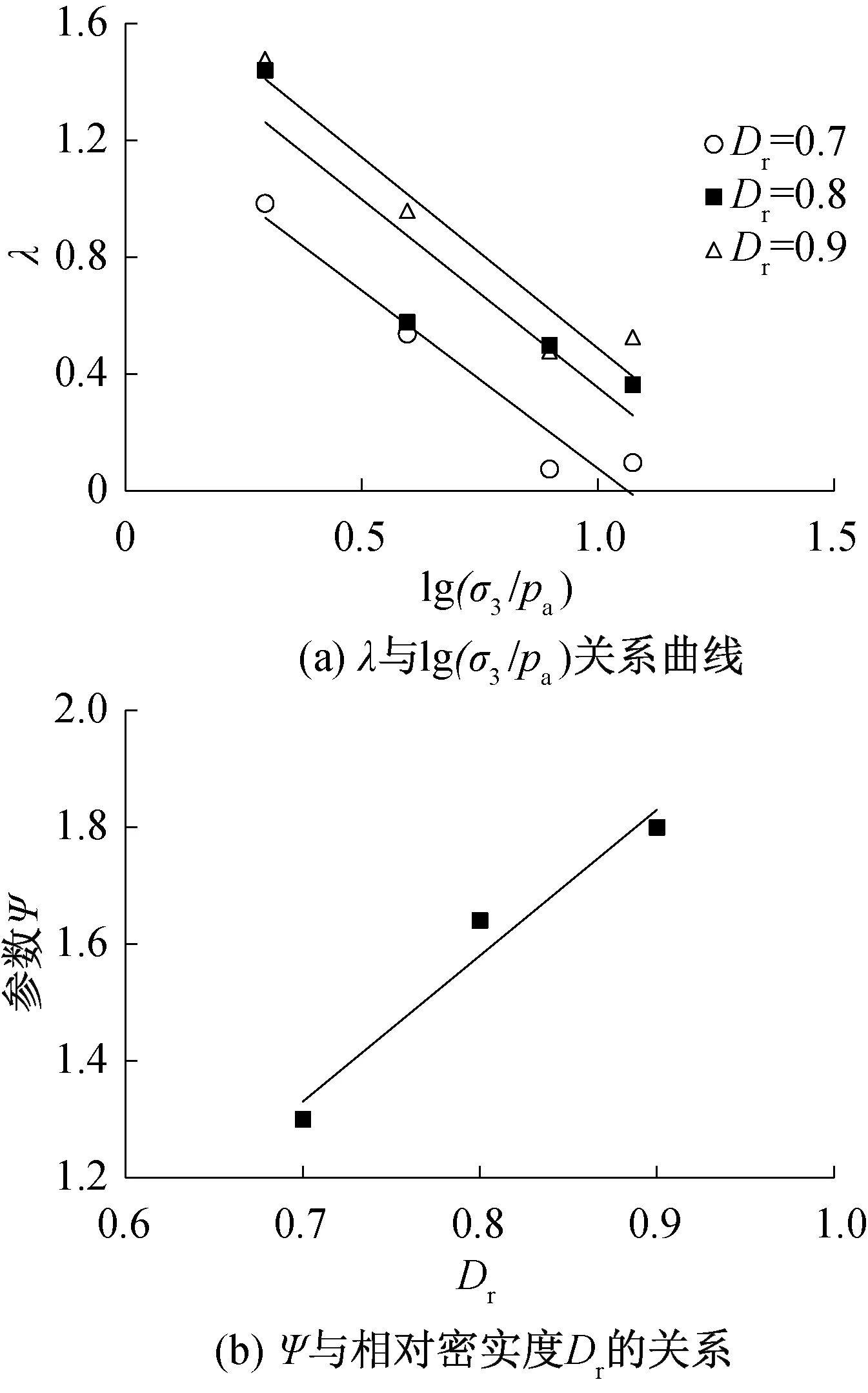
圖9 軟化系數(shù)λ與圍壓和相對密實(shí)度的關(guān)系曲線Fig.9 Relationship curves between λ and Dr

式(4)是根據(jù)此次試驗(yàn)數(shù)據(jù)歸納總結(jié)出來的，由于實(shí)驗(yàn)數(shù)據(jù)比較有限，因此存在一定的局限性，還需要更多的試驗(yàn)數(shù)據(jù)來驗(yàn)證其適用性。

2.2 體積變形特性分析

圖10至圖13給出不同圍壓下不同相對密實(shí)度的體積應(yīng)變和軸向應(yīng)變關(guān)系曲線，從圖中可以看出，在同一圍壓下，隨著相對密實(shí)度的增大，試樣的剪脹性逐漸變強(qiáng)，在εv-εa曲線上表現(xiàn)為對應(yīng)相同的軸向應(yīng)變εa，相對密實(shí)度大的試樣曲線對應(yīng)的體積應(yīng)變εv更小。在同一相對密實(shí)度下，隨著圍壓的增大，試樣的剪脹性逐漸減弱，在εv-εa曲線上表現(xiàn)為對應(yīng)相同的軸向應(yīng)變εa，圍壓大的試樣曲線對應(yīng)的體積應(yīng)變εv更大，特別是在圍壓為1 200 kPa時，試樣最終表現(xiàn)出來的體積變形都為剪縮。

圖10 200 kPa圍壓下不同相對密實(shí)度εv-εa關(guān)系曲線Fig.10 εv-εa curves of different relative density under 200 kPa confining pressure

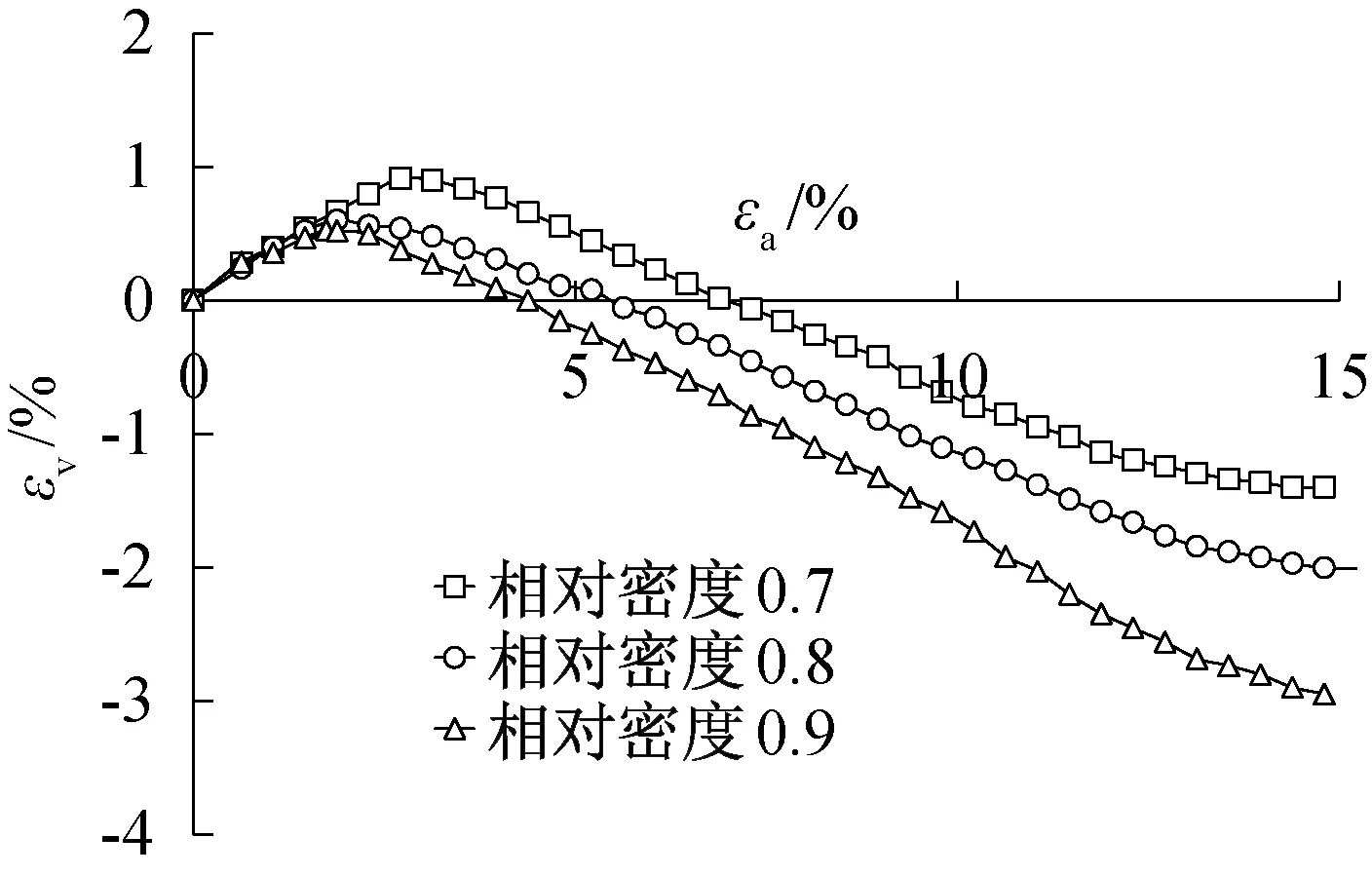
圖11 400 kPa圍壓下不同相對密實(shí)度εv-εa關(guān)系曲線Fig.11 εv-εa curves of different relative density under 400 kPa confining pressure

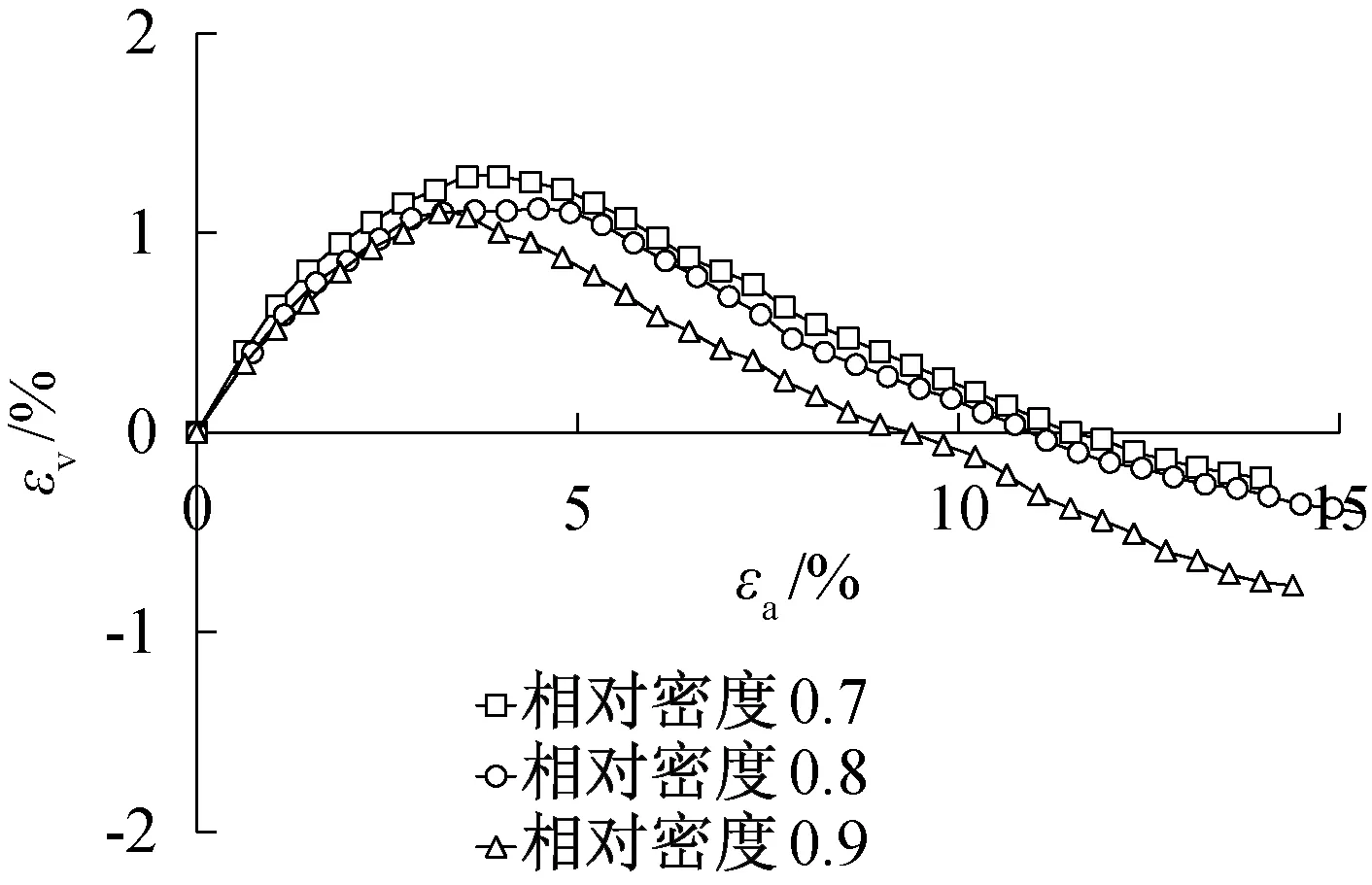
圖12 800 kPa圍壓下不同相對密實(shí)度εv-εa關(guān)系曲線Fig.12 εv-εa curves of different relative density under 800 kPa confining pressure

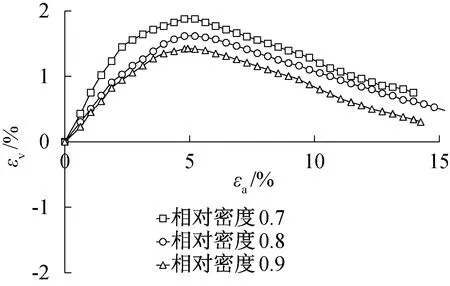
圖13 1 200 kPa圍壓下不同相對密實(shí)度εv-εa關(guān)系曲線Fig.13 εv-εa curves of different relative density under 1 200 kPa confining pressure

2.3 強(qiáng)度特性分析

為了分析相對密實(shí)度對試樣破壞時偏應(yīng)力的影響，整理得出試樣破壞偏應(yīng)力比(σ1-σ3)f/σ3。發(fā)現(xiàn)在同一圍壓下，破壞偏應(yīng)力比(σ1-σ3)f/σ3與相對密實(shí)度Dr成正相關(guān)；當(dāng)圍壓σ3分別為200、400、800、1 200 kPa時，相對密實(shí)度Dr每增大0.1，破壞偏應(yīng)力比平均相應(yīng)增加0.794、0.403、0.364、0.324，可以看出當(dāng)圍壓增大到一定值時，相對密實(shí)度對破壞偏應(yīng)力比的影響越來越小，原因可能是高圍壓導(dǎo)致了粗粒料顆粒的破碎，間接地增大了粗粒料的密實(shí)度。

表3整理了不同相對密實(shí)度試樣破壞時的殘余偏應(yīng)力(σ1-σ3)r，這里認(rèn)定殘余偏應(yīng)力是指試樣在某個圍壓下剪切至最大應(yīng)變時的偏應(yīng)力。

表3 不同相對密實(shí)度試樣破壞時的殘余偏應(yīng)力(單位：kPa)

從表3可以看出，不同相對密實(shí)度試樣的最終殘余偏應(yīng)力基本上都很接近。對同一圍壓下的殘余偏應(yīng)力求其平均值，用qr表示；同時整理出相對偏差值|(σ1-σ3)r-qr|/qr，用R來表示，如表4所示，除了在200 kPa、Dr=0.7以及200 kPa、Dr=0.9時，R有點(diǎn)大以外，其余點(diǎn)的相對偏差值都小于5%。將不同圍壓下的R求平均值，得出結(jié)果為3.72%。由此可見，相對密實(shí)度對殘余偏應(yīng)力或殘余強(qiáng)度影響較小。

表4 不同相對密實(shí)度試樣殘余偏應(yīng)力相對偏差R(%)

依據(jù)試驗(yàn)結(jié)果，進(jìn)一步整理出三種不同相對密實(shí)度試樣進(jìn)行固結(jié)排水剪切試驗(yàn)得到的抗剪強(qiáng)度指標(biāo)列于表5中。

表5 不同相對密實(shí)度試樣三軸固結(jié)排水剪切試驗(yàn)強(qiáng)度指標(biāo)

由表5數(shù)據(jù)可知，隨著相對密實(shí)度Dr的增大，不論是線性強(qiáng)度參數(shù)還是非線性強(qiáng)度參數(shù)都是增大的，而且相對密實(shí)度和強(qiáng)度參數(shù)之間表現(xiàn)出較好的變化規(guī)律，可以近似用直線進(jìn)行擬合，關(guān)系式為：

c=f1Dr+g1

(5)

φ=f2Dr+g2

(6)

φ0=f3Dr+g3

(7)

Δφ=f4Dr+g4

(8)

式中f1，f2，f3，f4和g1，g2，g3，g4為擬合參數(shù)，分別為17.15，1.05，2.05，0.75和108.23，38.70，48.27，7.67。用線性函數(shù)式(5)到式(8)擬合的結(jié)果如圖14和圖15所示。

圖14 線性強(qiáng)度參數(shù)與Dr的關(guān)系曲線Fig.14 Relation curve between linear strength parameters and Dr

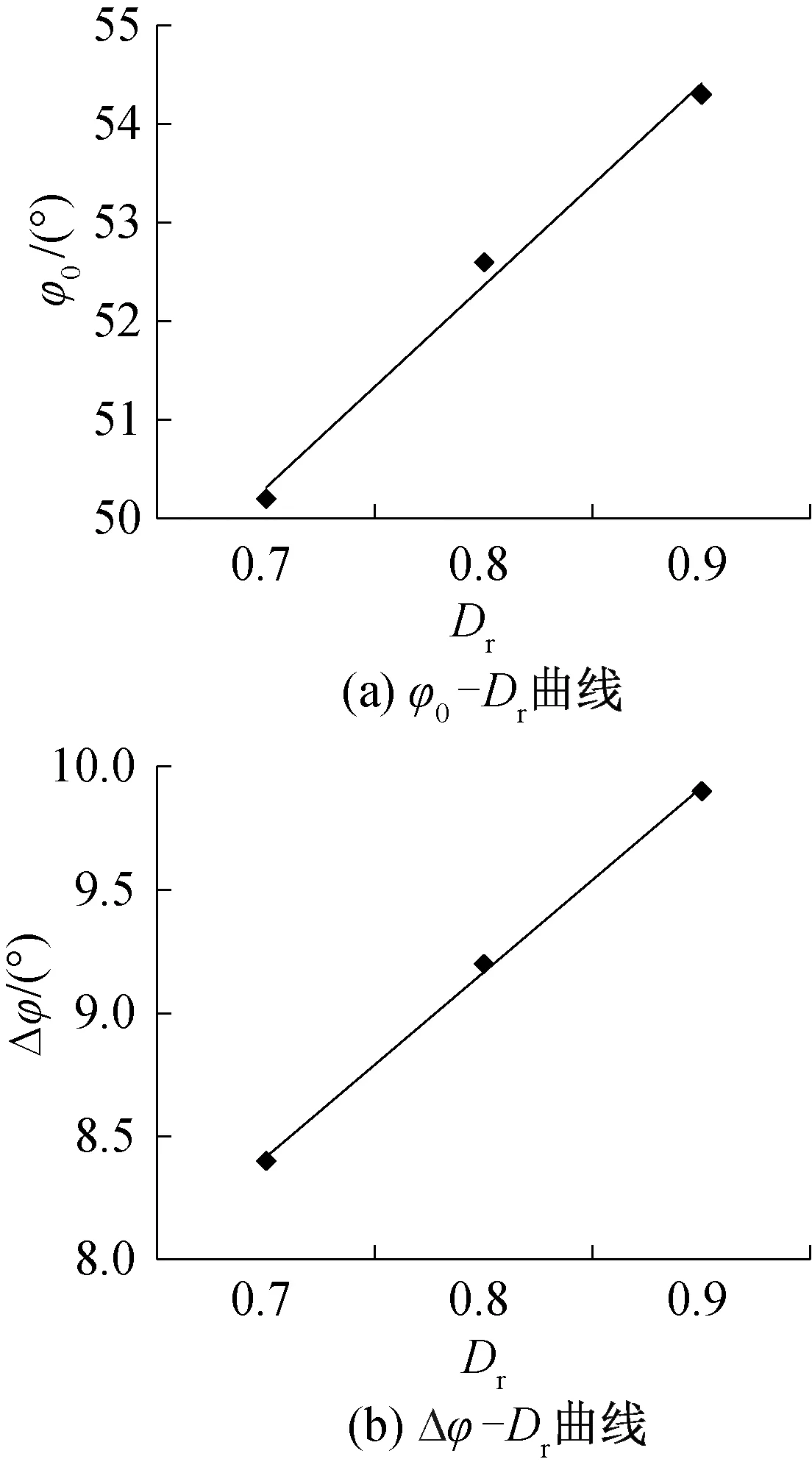
圖15 非線性強(qiáng)度參數(shù)與Dr的關(guān)系曲線Fig.15 Relation curve between nonlinear strength parameters and Dr

從圖14和圖15可以看出不論是采用線性強(qiáng)度參數(shù)，還是采用粘聚力等于零的非線性強(qiáng)度參數(shù)進(jìn)行擬合，得出來的曲線擬合程度都很高，計(jì)算得出后者擬合曲線的R2分別為0.990 4和0.998 5，可以看出采用非線性強(qiáng)度參數(shù)與相對密實(shí)度Dr擬合的效果更好，原因可能在于土體在高圍壓下存在顆粒破碎的現(xiàn)象，土體的強(qiáng)度包線往往表現(xiàn)出向下彎的趨勢，而不再是一條直線。

通過研究非線性強(qiáng)度指標(biāo)值φ0、Δφ與相對密實(shí)度Dr呈現(xiàn)出的線性關(guān)系，如果能夠測得覆蓋層粗粒料的現(xiàn)場干密實(shí)度或換算出相對密實(shí)度，則根據(jù)此線性關(guān)系能夠推得現(xiàn)場土料的非線性強(qiáng)度指標(biāo)，這對于在實(shí)際工程中確定土體強(qiáng)度具有重要的參考價值。

3 結(jié)論

本文通過對某大壩覆蓋層粗粒料制作試驗(yàn)替代料并進(jìn)行不同相對密實(shí)度下的常規(guī)三軸試驗(yàn)，研究了不同相對密實(shí)度對粗粒料應(yīng)力應(yīng)變和強(qiáng)度特性的影響，主要得出以下結(jié)論：

1)同一相對密實(shí)度下，隨著圍壓的增加，軟化現(xiàn)象更加明顯，峰值強(qiáng)度隨之增加，出現(xiàn)強(qiáng)度峰值時的軸向應(yīng)變值也逐漸增加；同一圍壓下，隨著相對密實(shí)度的增加，峰值強(qiáng)度也逐漸變大，但是出現(xiàn)強(qiáng)度峰值時的軸向應(yīng)變值反而逐漸減小。

2)在同一圍壓下，隨著相對密實(shí)度的增大，曲線表現(xiàn)出更加明顯的軟化現(xiàn)象，初始切線模量Ei逐漸增大。鄧肯模型參數(shù)Rf和n基本不受相對密實(shí)度的擾動，參數(shù)K與相對密實(shí)度近似呈線性變化規(guī)律；引入了新的參數(shù)軟化系數(shù)λ，建立了軟化系數(shù)λ與圍壓和相對密實(shí)度的關(guān)系式，可作為反映試驗(yàn)粗粒料軟化特性規(guī)律的參考。

3)在同一圍壓下，隨著相對密實(shí)度的增大，試樣的剪脹性逐漸增強(qiáng)；在同一相對密實(shí)度下，隨著圍壓的增大，試樣的剪脹性逐漸減弱，特別在圍壓為1 200 kPa時，試樣最終表現(xiàn)出來的體積變形都為剪縮。

4)相對密實(shí)度和圍壓對試樣破壞時的偏應(yīng)力影響較大，試樣的殘余強(qiáng)度受相對密實(shí)度的影響較小。當(dāng)圍壓分別為200、400、800、1 200 kPa時，相對密實(shí)度Dr每增大0.1，破壞偏應(yīng)力比平均相應(yīng)增加0.794、0.403、0.364、0.324。

5)線性強(qiáng)度參數(shù)和非線性強(qiáng)度參數(shù)均隨相對密實(shí)度Dr的增大而增大；其中采用非線性強(qiáng)度參數(shù)與相對密實(shí)度Dr擬合的效果更好，可依此線性關(guān)系推得現(xiàn)場粗粒料的非線性強(qiáng)度指標(biāo)，以為實(shí)際工程中確定強(qiáng)度參數(shù)提供參考。