礦柱尺寸設計及穩定性的數值模擬分析
范文濤 紀永剛 于文杰 張 杰
(1.錫林郭勒盟山金白音呼布礦業有限公司;2.北京科技大學土木與資源工程學院)
地下采礦工程中,礦柱能夠有效控制頂板跨度過大引起的變形破壞,保障頂板圍巖穩定。在上覆巖層荷載作用下,礦柱寬度過小,容易產生失穩;礦柱寬度過大,會損失礦量。因此,科學合理地設計永久礦柱的寬度對維持采場穩定、提高資源利用率等具有重要意義。
針對礦柱穩定性問題,國內外學者在礦柱強度公式推導、安全系數計算等方面取得了豐碩成果[1-3]。尹升華等[4]基于礦柱荷載與失穩勢函數分析了影響礦柱穩定性的因素,進一步簡化矩形礦柱安全系數的計算公式;宋衛東等[5]比較了條形礦柱與方形礦柱的強度,建立了二者與其主要影響因素間的回歸方程;陳光飛等[6]考慮充填體對礦柱的強化作用,推導出了礦柱安全系數表達式。李傳奇等[7]使用地質強度指標GSI分析了硬巖柱穩定性,基于預測應力估算其安全系數。Bradley等[8]對礦區深部花崗巖礦柱進行現場監測,研究了采礦活動中礦柱的位移和應力變化特征。鐘福生等[9]研究了房柱法采礦中不同開采深度下的合理礦柱尺寸。
白音呼布礦區最大開采深度已達900 m,地應力環境復雜,圍巖較為破碎,合理留設礦柱能夠保證采場圍巖穩定。采用從屬面積法估算礦柱的強度和軸向壓應力,從而計算礦柱尺寸,并用數值模擬驗證其合理性,為類似礦山礦柱穩定性設計提供參考。
1 礦柱強度理論計算
1.1 礦柱壓力確定
采場開挖過程中,應力擾動及應力重分布導致圍巖強度弱化,礦柱承載能力相較完整巖石有所降低,其力學參數應進行折減。根據Hoek-Brown強度準則,計算如下。
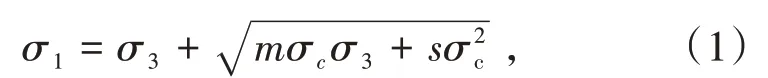
式中,σ1、σ3為巖體破壞時的最大主應力和最小主應力,MPa;σc為試塊的平均單軸抗壓強度,MPa;m為反映巖石軟硬程度的常數;s為反映巖體破碎程度的常數。
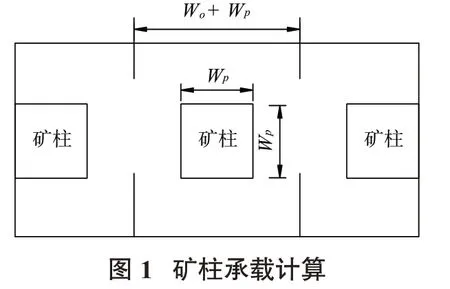
根據礦柱的承載機理,其表面承受的荷載為上覆巖體的重力。礦柱壓應力一般采用從屬面積法來估算礦柱平均軸向壓應力[10],如圖1所示,其承載的面積為礦柱自身的面積和礦柱分攤的開采面積之和,計算公式如下。

式中,σp為礦柱上表面承受荷載,MPa;pzz為開采前應力場的垂向正應力分量,MPa;wp為礦柱寬度,m;wo為礦房跨度,m。
1.2 礦柱安全系數
根據式(1)和式(2)可得到永久礦柱安全系數的表達式,見式(3)。
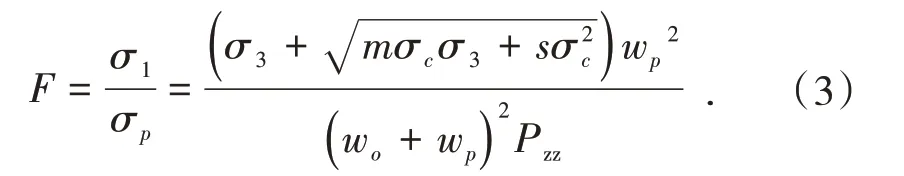
安全系數F>1時礦柱穩定,F<1時礦柱不穩定,安全系數越大越安全。在礦柱參數設計中,應充分考慮開采深度、充填體水平應力、礦房寬度、礦柱寬度因素的影響[6]。工程實踐表明,大多數礦山采用安全系數為1.2~1.5,礦柱未發生破壞[11],因此,安全系數取為1.2。
2 工程算例
2.1 工程條件
山金白音呼布礦區位于內蒙古東烏珠穆沁旗東北部,礦體主要位于礦區北部NWW向構造蝕變破碎帶中。礦體近礦圍巖多為二長花崗巖,部分為泥質板巖,圍巖破碎、地壓作用顯著。從礦巖地質條件來看,其穩定性主要受變形地壓和破碎帶影響。
針對礦巖體不同穩定程度,礦山主要的采礦方法為上向水平分層充填采礦法和上向進路式膠結充填采礦法,采場沿礦體走向布置,采場長為100 m,寬為礦體水平厚度,分段高度10.5 m。根據礦區工程所處區域巖性、埋深的不同,有針對性的采取不同的支護方式,主要以錨桿加金屬網片支護為主。
2.2 礦柱尺寸設計
以400 m中段4055采場為例,進行礦柱強度及穩定性分析。采場施工圖如圖2所示。

礦柱寬度與頂板極限跨度有關,計算礦柱尺寸時應考慮頂板極限跨度。該采場進路跨度控制在4~6 m,分層垂直高3.5 m。采用點荷載強度測試得到試塊的平均單軸抗壓強度78.75 MPa,礦柱在二維應力狀態時,s=0.5,根據Hoek-Brown強度準則對區域巖體力學參數進行折減。由式(1)計算礦柱巖體強度為55.68 MPa;當安全系數取1.2時,由式(2)可得礦柱上表面承受荷載為46.4 MPa;開采前應力場的垂向正應力分量為12 MPa,因此,方形礦柱寬度為6.25 m。
3 數值模擬
3.1 模型建立
根據白音呼布礦山井下礦體埋深,選取+400~+350 m中段,采用FLAC3D數值模擬軟件建立4055采場礦柱模型。簡化的模型具有對稱性,模型尺寸取實際的四分之一,能有效提高模型的計算效率。模型坐標軸Y為礦體厚度方向,X軸為礦體走向,Z軸為鉛垂方向,共劃分32 959個單元,30 963個節點。
礦區模型整體施加重力場,底部施加位移邊界,巖體周邊施加應力邊界。根據礦區實測地應力場分布特征,上邊界施加垂直載荷約為12 MPa,最大水平主應力為24 MPa(Y軸方向),最小水平主應力為9.6 MPa(X軸方向)。本構模型選用應變軟化模型,巖石材料表現為每2%切向變形時,黏聚力下降,摩擦角變化為6°。為了確定礦柱可支撐的最大荷載,模型頂部以-5×10-6m/步的恒定速度垂直下移。巖體物理力學參數:巖石密度為2 700 kg/m3,體積模量為14.1 GPa,剪切模量為8.9 GPa,泊松比為0.26,黏聚力為2.85 MPa,內摩擦角為46.55°,抗拉強度為0.2 MPa。
3.2 結果分析
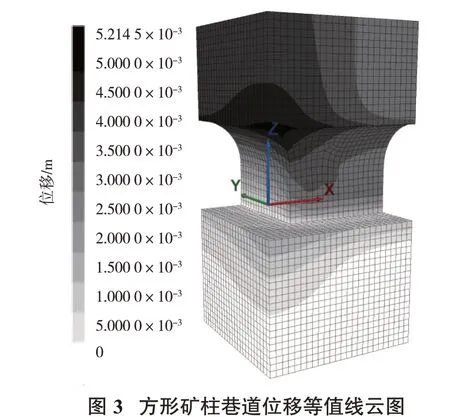
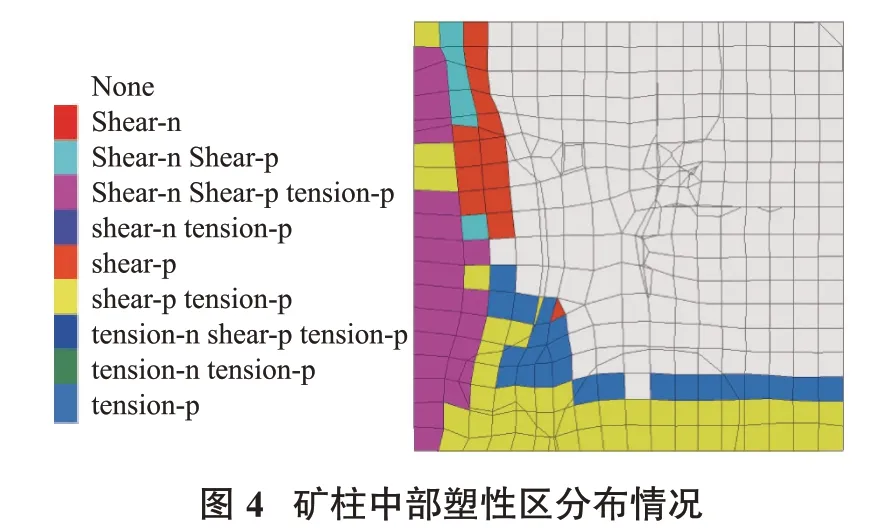
開挖后的方形礦柱巷道位移等值線云圖如圖3所示。在交叉巷道的頂板中心處出現最大位移,約為5.2 mm;X軸方向一側邊墻位移大于Y軸方向一側位移。圖4為礦柱中部塑性區分布情況,可以看出塑性區從邊墻0.8 m到交叉點柱角處1.7 m深;X軸方向一側張拉塑性區分布較多,Y軸方向一側剪切塑性區分布較多(圖4)。巷道內最大主應力出現在巷道底角部位,應力高達43.8 MPa。
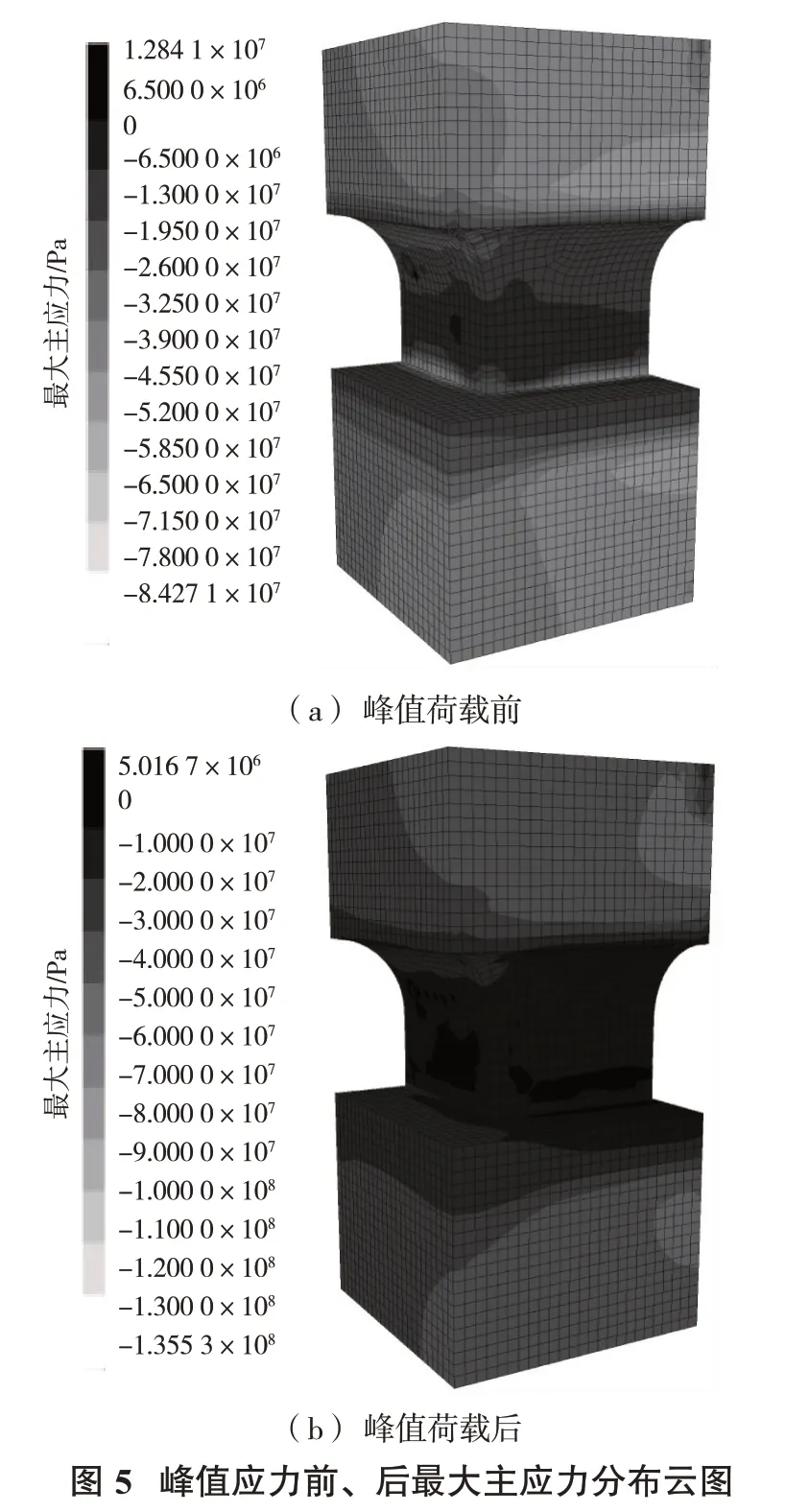
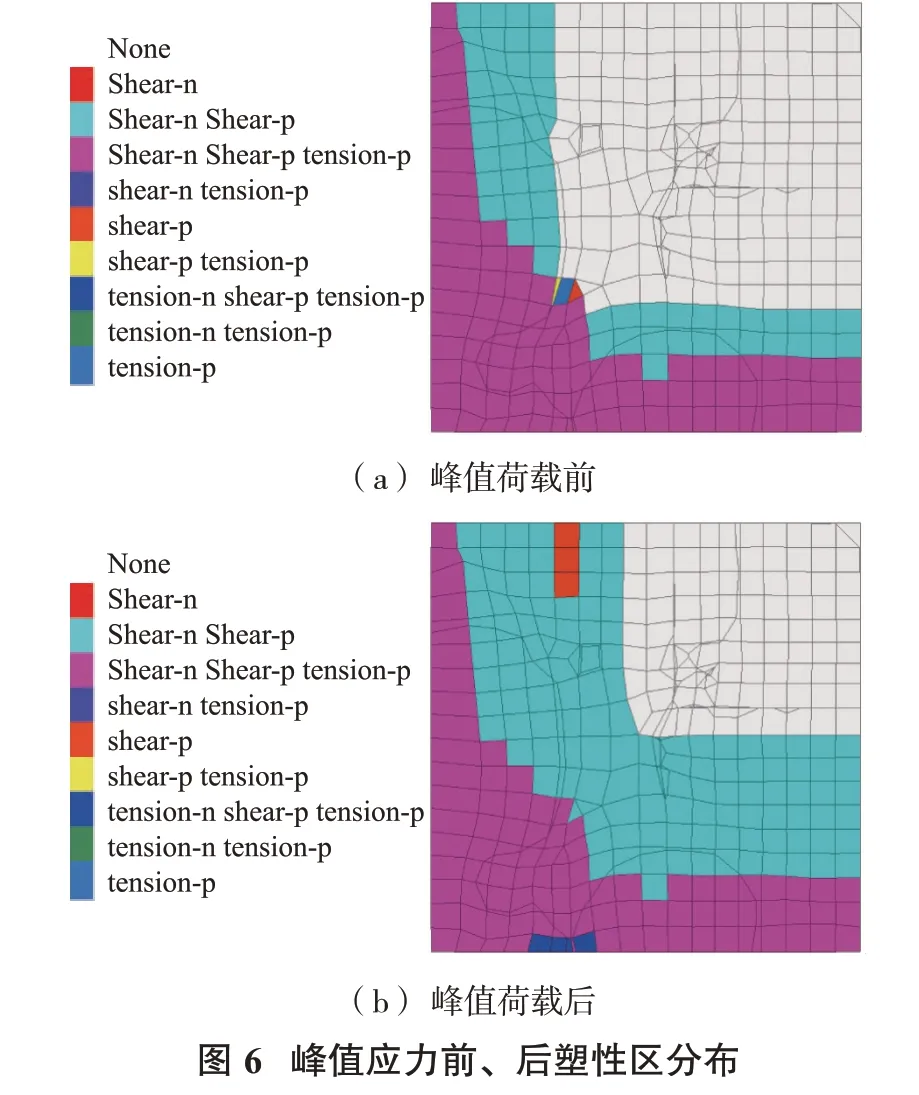
當礦柱模型頂部由應力邊界條件切換為速度邊界條件,礦柱最終承載力達57 MPa,與理論計算結果相近。礦柱峰值荷載前(51.6 MPa)、后(53.5 MPa)的最大主應力分布云圖和塑性區分布情況分別如圖5、圖6所示。隨著模型頂部位移加載,礦柱破壞范圍逐漸增大:峰前為巷道邊墻部位的剪切塑性區的發展,峰后表現為巷道邊墻與交叉點柱角部位的共同發展,且峰后最大主應力增大很多。
3.3 長寬比對礦柱穩定性的影響
當礦柱承載面積一定,長寬比由1∶1變成1∶0.7和1∶0.5時,得到的礦柱峰值應力及位移變化信息匯總如表1所示,礦柱承載應力隨計算時步增加的變化曲線如圖7所示。

?
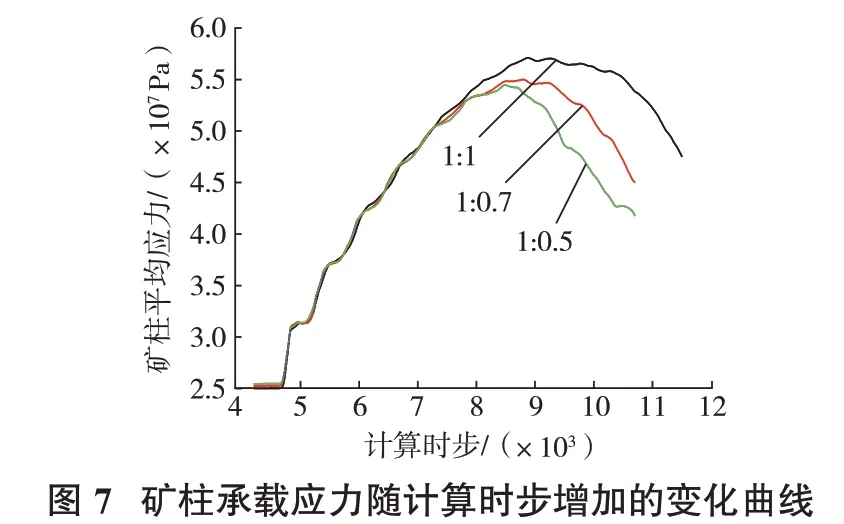
根據數值模擬結果可知,巷道中心交叉點處的位移和塑性區分布以及主應力分布情況隨礦柱長寬比變化不大。當邊界條件改變后,礦柱承受的應力在達到峰前約53 MPa之前基本一致;此后,應力變化出現差異:在礦柱最大承載能力隨長寬比的減小而降低,降幅較小,僅為3%和5%;峰后應力降低速率不同,長寬比較大的模型表現出的脆性破壞特征更為顯著。
4 結論
基于Hoek-Brown強度準則對采場巖體的力學參數進行折減,然后進行采場礦柱尺寸的理論計算。采用數值模擬方法對設計的礦柱進行穩定性分析,得到以下結論。
(1)采用從屬面積法估算白音呼布井下礦柱承受荷載,并選取安全系數1.2進行礦柱尺寸設計,得到4055采場方形礦柱寬度為6.25 m。
(2)開挖后的方形礦柱巷道交叉中心點處位移最大,礦柱峰值應力時的位移達到17.5 mm,巷道內集中應力出現在巷道底角部位;最大主應力方向的圍巖多發生剪切破壞,最小主應力方向多為張拉破壞。
(3)當承載面積一定時,礦柱的長寬比值越大,承載能力降低,且脆性破壞特征明顯。相較于長方形礦柱,方形礦柱穩定性最好。

