基于POI和交易數據的住宅特征價格分析

張寅 駱忠祥 何蕙 華恒祺 袁慶鋒 陳暉

摘要：以無錫市為例，選取2019年7月至2020年6月的商品住宅交易數據和備案樓盤信息。通過房屋代碼匹配交易數據形成監測格網，并定位樓盤點。結合POI數據，選取3類特征因素，21個特征因子，分區域構建樓盤住宅的特征價格線性模型。在鄰里特征因子的計算中引入特征統計距離，使用增量空間自相關工具測算。回歸分析中，在OLS和GWR回歸基礎上使用探索性回歸工具，分析各區域有效因子的所有組合，得到變量顯著性匯總數據。研究可有效支持“一區一策”政策的制定。

關鍵詞：住宅特征價格;POI;網簽數據;探索性回歸;一區一策

中圖分類號：F293.35 文獻標識碼：A

文章編號：1001-9138-（2021）04-0035-43 收稿日期：2021-03-17

作者簡介：張寅，工程師，注冊測繪師，無錫市曦晨測繪有限公司。

駱忠祥，經濟師，無錫市房屋交易管理中心。

何蕙，工程師，無錫市曦晨測繪有限公司。

華恒祺，無錫市房屋交易管理中心。

袁慶鋒，高級工程師，注冊測繪師，無錫市曦晨測繪有限公司。

陳暉，經濟師，無錫市房屋交易管理中心。

基金項目：無錫市科協軟科學研究重點課題“時空大數據支持下深化無錫市房產市場監測分析問題研究”（KX-20-C010）。

1 引言

2017年以來，中央多次強調，要堅持“房子是用來住的、不是用來炒的”定位，綜合運用金融、土地等手段，加快建立促進房地產市場平穩健康發展的長效機制。隨著各地相繼落實“一城一策、因地制宜”，監管部門迫切需要通過大數據應用，實時獲取各城市市場交易情況、價格走勢、風險預警等相關數據信息。

利用商品房合同網上備案制度，對房地產市場的交易進行全面管理，能夠同時監測所有交易數據。然而，這樣的市場監測系統僅是對數據進行簡單的整合與對比，對供求進行科學研判的深度分析不夠。

在無錫市房屋交易管理中心（以下簡稱“交易中心”）的支持下，我們進行了相關嘗試。首先，以新增住宅面積數據為例，利用房產測繪數據結合房地產市場數據，以1：500房產分幅格網為基準，在空間上定位了房地產市場運行的數據指標，構建了分辨率適宜的空間統計框架;其次，在Mann-Kendall方法的支持下，對新增住宅面積的分布狀況、時空變化趨勢作了分析，驗證空間統計框架的有效性。借此，交易中心希望能夠深化空間統計框架的應用，將監測數據在空間和時間維度上進行分析，為房產市場的調控監管提供決策支持。

城市住宅價格除了受經濟、社會等因素影響外，與空間地理位置的關系也越來越密切。符合距離城市中心區域近、周邊公共交通條件良好、所處學區內學校質量高、周邊醫療衛生條件好、環境質量條件好等條件的住宅小區價格較高。由于住宅空間位置不同，價格出現明顯差異的現象稱為住宅價格空間分異。

研究認為，城市住宅價格空間分異的核心影響因素是小區建設檔次與水平，不同類型住宅子市場的價格影響因素各不相同;其主要驅動力是特定住宅類型與檔次建設的區位指向、特定收入階層的空間集聚、公共物品投資的空間差異、城市居住用地擴展與城市更新的區位指向。

目前，學術界對房地產價格空間分布規律的研究可歸結為兩類：一類是利用GIS的空間分析和地統計分析，對價格的空間分布格局進行研究;另一類是通過建立特征價格模型量化分析影響房價的各因素。

對房地產價格空間分異模式的研究方法主要分為計量經濟學方法和GIS空間分析方法，其中前者主要為一些多元線性回歸和聚類分析，后者則采用K氏估計法、克里金插值法和探索性空間分析（ESDA）技術等方法，并結合相關的地理信息系統軟件對價格的空間分異模式進行分析。近年來，對房地產價格空間分異的研究在空間尺度上出現多樣化的趨勢，分析的尺度從全國和省級，向區域和市縣級發展。

在全國和省級層面上，有利用2002-2015年期間我國31個省、市、自治區的面板數據，并按區域劃分東部、中部和西部三類，通過構建空間面板模型分析3大區域的房地產價格空間相關關系和影響因素。有基于不同省份2000-2015年的動態面板空間數據，運用二階段空間自回歸模型方法分析人均國內生產總值、地區人口數、人均受教育程度、人均收入等因素對房地產價格的影響。

在區域和市縣級層面上，有以長三角135個區縣為研究對象，在通過分異度指數測度發現2014-2016年各區縣商品房價差異增大的基礎上，以商品房單位面積成交均價為因變量，提取16項房價影響因素為自變量，通過逐步回歸和地理加權回歸進行定量分析。有基于我國國土勘測規劃院中國城市地價動態監測系統中35個大中城市2010-2017年住宅地價房價比的監測數據，運用描述性分析、探索性空間數據分析和面板空間杜賓模型進行研究。此外，也不乏在單個城市的尺度上，利用城市住宅價格數據，使用空間自相關、變異函數、克里金空間插值等方法，分析城市住宅價格空間特征，并選取適宜的影響因子構建一般特征價格模型或基于地理加權回歸（GWR）方法的特征價格模型。

Lancaster和Rosen被普遍認為是特征價格模型的奠基人，有效地推動了特征價格模型的發展。特征價格理論認為，地價綜合反映了土地具備的如面積、區位、容積率、規劃條件等不同的品質或特征，土地價格是隨著其中的某個品質或特征改變而改變的。針對住宅價格，研究將影響因素分為四類：區位因素、鄰里因素、建筑因素、時間因素，并具體劃分為11個變量因子。

住宅價格影響因素數據的獲取能夠以POI為來源。POI是指一些與人們生活密切相關的地標建筑和地理實體的點數據，描述了這些地理實體的空間位置和屬性信息。利用POI數據結合特征價格模型研究城市房價也成為可能。在老工業區的可持續發展決策支持研究中，基于POI大數據并結合GWR模型，篩選可能影響房價變化的因素，探索不同因素對房價產生影響的空間差異性。以重慶、成都、武漢3個城市的主城區為例，收集其房價、夜間燈光、POI數據和其他數據，探索各城市房價空間分布特征，探討影響房價空間分布的因素。以住宅和零售業興趣點為數據源，基于空間核密度分析提取住宅和各類零售業的空間聚類形態，量化表達商住空間布局的相關性，并在此基礎上運用地統計方法測算房價的空間異質性及其與零售業態空間布局的差異特征。結合成都市住宅小區成交均價和相關POI數據，分析診斷住宅價格，解析空間分布特征，構建HPM與GWR模型。以烏魯木齊市為研究區域，基于綠地周邊POI數據，從區位、建筑結構、鄰里關系三個維度選取解釋變量，構建住宅市場特征價格模型并結合彈性與邊際價格分析，量化了烏魯木齊市公園綠地對住宅價格的影響。可見，POI數據能夠很好地支持住宅特征價格的研究，為房產市場監測分析的深化和改進提供數據支持。

研究嘗試利用分幅格網將商品住宅交易數據定位到空間，并結合價格特征因素和POI數據，以無錫市為例構建住宅特征價格模型，分析商品房住宅價格與相關因素的關系。希望借助研究，支持相關調控政策的制定和實施。

2 數據來源與處理

無錫市轄梁溪區、錫山區、惠山區、濱湖區、新吳區5個區及江陰、宜興2個縣級市。研究以無錫市的5個行政區為對象。

交易數據來自交易中心，包括商品房成交數據、商品房核準樓盤數據等。研究選取2019年7月至2020年6月的商品房住宅交易數據，并提取交易涉及的備案樓盤信息。通過房屋代碼將交易數據匹配到圖幅格網形成監測格網，利用監測格網定位樓盤位置得到樓盤點。隨后，將交易數據按樓盤匯總至樓盤點，并匹配樓盤信息。

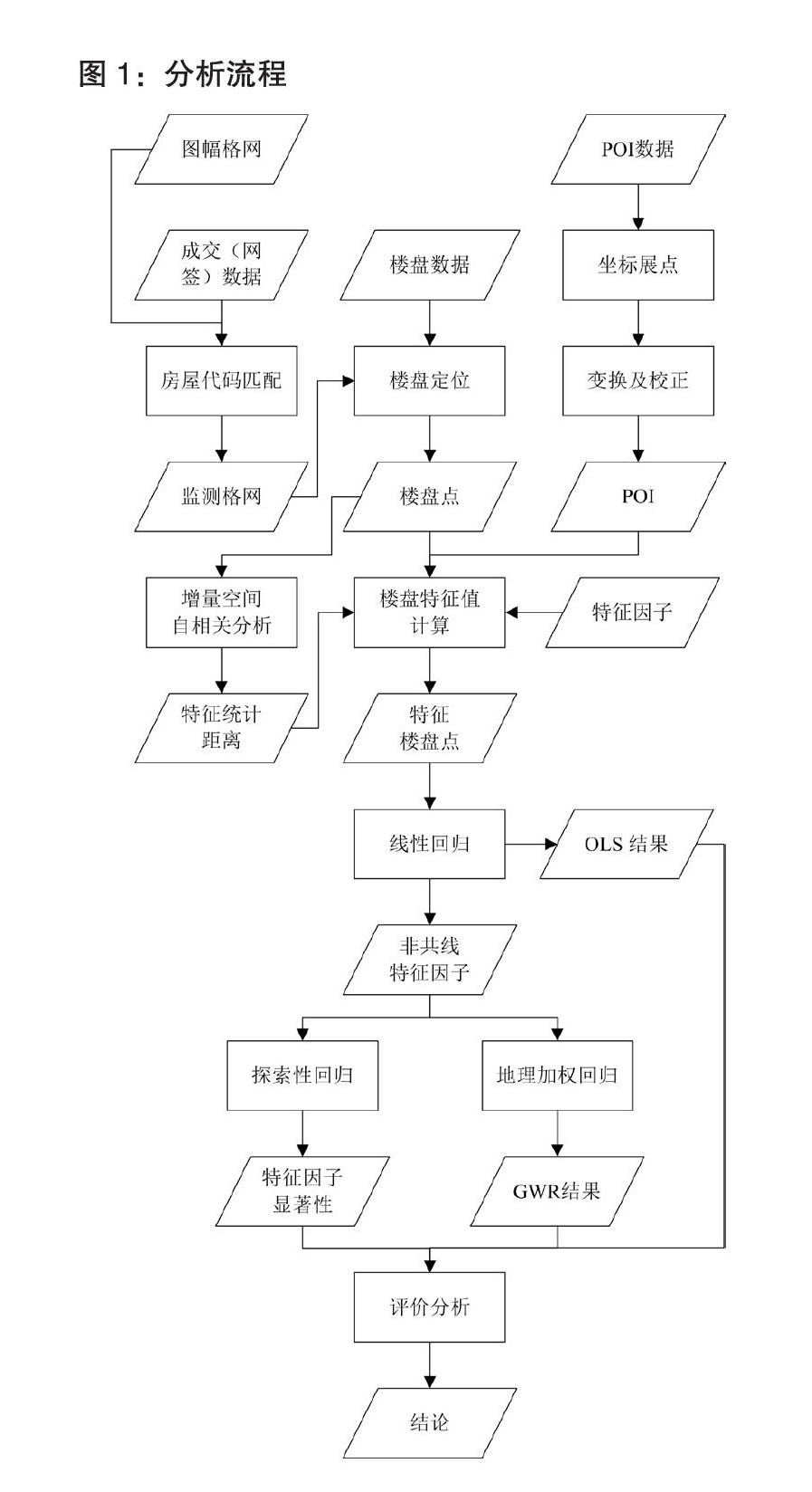
POI數據來自北京大學開放研究數據平臺，源自高德地圖，地域覆蓋全國。研究中，對無錫市范圍內的POI數據，使用位置的經緯度坐標進行展點。再通過投影、坐標變換、空間校準等操作將POI與監測格網的坐標系相匹配。特征因素數據采用處理后的POI數據。數據的處理和整個分析流程，如圖1所示。過程中使用的分析工具來自ArcGIS的空間統計工具箱。

3 特征價格模型

特征價格模型以價格為因變量，影響價格的特征因素為自變量，通過回歸分析得出價格與特征因素之間的關系。這種關系以回歸系數的形式表示，系數的數值表示自變量與因變量之間關系的強度和類型。當關系為正時，系數的符號為正;當關系為負時，符號為負。如果關系很強，則系數也相對較大;如果關系較弱，則趨于零。

常用特征價格模型有3種，線性模型、對數模型和半對數模型，如表1所示。

式中，P為價格，α為截距，ε為殘差，Xi為特征因素，βi為特征因素對應的系數。研究直接使用最為通用的線性模型。

4 特征因素

參考已有研究對特征因素的選擇，結合現有研究和數據的情況，選取3類特征因素，21個特征因子。特征因子及其量化，如表2所示。

文獻中一般使用建筑特征因素，此處使用樓盤特征是因為，研究以監測格網統計數據，并將交易數據匯總至所屬的備案樓盤。模型中，以樓盤平均成交價格作為因變量。樓盤特征是對該樓盤的住宅規模、銷售時間、住宅成交情況的描述，共計5個特征因子。

區位特征描述樓盤的地理位置，包括自然、經濟和交通等方面，主要以POI與樓盤點的歐氏距離度量。選取的POI包括交通、民生、商業、政府等設施，共計7個特征因子。

鄰里特征是對樓盤周邊情況的描述，研究從出行、鄰里、購物、教育、就業等角度選取樓盤周邊特定范圍內POI的數量，共計9個特征因子。其中，教育和就業使用固定距離為分析范圍，地鐵站使用相鄰地鐵站平均距離的1/2為閾值。在周邊樓盤、超市便利店、公交站臺等因子的計量上引入特征統計距離。

5 特征統計距離

所謂特征統計距離是指，在目標對象周邊統計某一特征因子使用的距離。引入特征統計距離，一方面是空間關系建模的需要，另一方面是建模分析工具的要求。空間關系模型需要將對象所處的空間和對象間的空間關系整合到模型中，并且建模需要對應不同對象空間關系的尺度。此外，軟件提供的空間統計工具需要輸入空間關系概念化的方法，或者提供空間約束的參數。這些方法和參數的確定離不開對空間關系尺度的測定。研究中使用增量空間自相關（Incremental Spatial Autocorrelation）工具測算特征統計距離。

增量空間自相關工具能夠對一系列逐漸增大的距離做空間自相關測算，評價各距離空間聚集的程度，其程度由返回的z得分確定。隨著距離的增大，z得分會出現多個峰值。通常選擇第一個統計顯著性峰值對應的距離作為空間關系尺度，也就是研究中使用的特征統計距離。

測定空間關系尺度前，對全市樓盤點數據均價字段做了初步的全局空間自相關分析，得到全局Moran's I值為0.6938，z得分為11.6844和p值為0.00。結果顯示數據呈現空間集聚。

隨后，對全市數據做增量空間自相關分析發現，z得分隨著距離增大而持續增加，不存在峰值。結合工具說明和數據分析，研究認為全市范圍內存在多個尺度的樓盤空間集聚過程。故而，需要在更小的空間尺度上進行分析。

在綜合考慮樓盤的分布、調控政策的實施、交易數據的敏感性等方面后，研究在行政區尺度上繼續進行分析。并且，由于馬山街道在地形上明顯不同于濱湖區的其他地區，將馬山街道單獨列出分析。行政區尺度的增量空間自相關結果，如表3所示。

在行政區尺度上，馬山街道的空間關系尺度最大，梁溪區的最小，其他區域都在300至400米左右。馬山街道的地形以丘陵為主，樓盤分布受地形影響嚴重。梁溪區是無錫的主城區，街道規劃尺寸與其它后開發的區域相比明顯較小，故而特征統計距離最小。

6 樓盤特征值計算

樓盤特征值的計算以樓盤點和POI等數據為輸入數據，特征因子、特征統計距離、地鐵站間距均值等為計算參數，使用Python調用ArcPy擴展包，編寫腳本程序實現。計算完成后，輸出表示樓盤位置、包含樓盤特征因子計算結果的特征樓盤點數據。

7 回歸分析

7.1 OLS和GWR回歸

對特征樓盤點數據的回歸分析調用普通最小二乘法（OLS）工具，使用特征價格線性模型。在回歸分析前，首先去除研究區域內不存在對象的特征變量。在回歸分析中，去除線性冗余部分，即方差膨脹因子（VIF） >7.5的變量。最后得到OLS回歸分析的結果，如表4所示。

在OLS回歸結果中，觀察到存在個別地區殘差稍微偏離正態分布的情況，且所有區域的殘差都觀察到空間自相關。隨后，對每個區域進行了地理加權回歸（GWR）分析，發現GWR回歸結果（表4）沒有明顯提升。研究認為，這是本次采用的數據和地理加權回歸分析工具造成的。

地理加權回歸分析工具需要設定核函數搜索帶寬，并且要求每個對象周邊的搜索結果數大于30，否則計算結果不可信。用于GWR分析的數據為樓盤點數據，在滿足搜索結果要求時，帶寬的計算結果幾乎等同于分析區域樓盤分布的半徑，遠大于區域的特征統計距離。在以后的研究中，需要延長分析時段，增加樓盤數目。

研究中發現，利用回歸分析工具得出的特征價格模型公式不能很直觀地支持相關決策的制定，并且直接給出價格擬合的模型參數信息過于敏感。我們希望能夠更好地評價各非共線因子的顯著程度、影響關系正負等情況，所以研究中進一步引入了探索性回歸工具。

7.2 探索性回歸

探索性回歸工具能夠根據用戶指定的指標，對輸入變量的所有可能組合進行評估，以尋找解釋因變量的最佳OLS模型。探索性回歸工具能夠給出變量顯著性的匯總數據，包括在所有組合中變量具有統計顯著性的比例（%顯著性），具有統計顯著性時呈正關系（%正數）和負關系（%負數）的比例。通過對比%負數和%正數的數值，可以檢查變量關系的穩定性。較強的預測因子始終具有較高的顯著性，且變量關系比較穩定。研究對每個區域的非共線因子作探索性回歸，變量顯著性結果，如表5所示。

8 因素評價分析

樓盤特征因素中，核準年數因子的顯著性最高，且變量關系最穩定，與價格呈負相關。住宅套數因子的顯著性在不同區域存在高低浮動，但與價格的關系是穩定的負相關。說明住宅價格高的樓盤住宅規模小，樓盤銷售周期越長售價越低。住宅平均成交面積因子僅在馬山和惠山區，存在比較強的穩定負相關。樓盤成交套數因子在每個區域都與價格呈現較強的正相關，說明交易量高的樓盤價格也高。

區位特征因素中，火車站距離因子在參與測算的區域都有一定的顯著性，但與價格的關系有變化。在梁溪區、新吳區、惠山區離火車站越遠，樓盤住宅價格越高。在錫山區卻存在顯著而穩定的負相關。景點距離因子在濱湖區、錫山區、新吳區與價格存在負相關，價格高的住宅靠景區更近，但在惠山區相反，梁溪區不明顯。從商業綜合體距離因子可以發現，高住宅價格的樓盤在濱湖區、梁溪區離商業綜合體更遠，但在錫山區、新吳區、惠山區靠近商業綜合體。三甲醫院所在區域，樓盤距離醫院越近房價越高。新吳區機場周圍，距離越遠樓盤房價越高。通過集市菜場距離因子發現，在濱湖區、新吳區高房價的樓盤靠近集市菜場，但在梁溪區、錫山區、惠山區則相反。在梁溪區、新吳區、惠山區均能發現高價格樓盤靠近人民政府所在地。

鄰里特征因素中，樓盤因子的統計顯著性在多數區域呈現穩定的正相關，說明周邊樓盤越多，樓盤的住宅價格越高。超市便利店因子和公交站臺數因子與樓盤價格的關系大多數呈現負相關，這似乎與常識相違背。需要考慮到的是，所用的商品住宅交易數據記錄的幾乎都是期房交易，少量尾盤現房交易。超市便利店、公交等在價格較高的期房樓盤周圍，樓盤周邊在建和已建地鐵線路的站臺個數因子對各個區域的影響各不相同。在顯著性較高的區域里，濱湖區和惠山區靠近已建線路的房價高，在建線路的房價較低。梁溪區高價格樓盤遠離地鐵線路，錫山區在地鐵線路周圍的樓盤都價格較高，新吳區靠近在建線路的房價較高。各個區域，在寫字樓、工業園區辦公樓周圍的樓盤價格較高，關系顯著而穩定。在幼兒園個數因子中，除錫山區外，高房價樓盤都遠離幼兒園。在小學個數因子中，除濱湖區外，高房價樓盤都靠近小學。在中學個數因子中，除錫山區外，高房價樓盤都靠近中學。

9 結論

利用POI和商品房住宅交易數據，結合特征統計距離能夠較好地構建住宅特征價格模型。模型對價格的解釋程度還有提高的可能，需要在后期研究中豐富樓盤特征的因子，包括樓盤容積率、綠化率、建筑密度等規劃信息。探索性回歸工具提供的變量顯著性匯總數據能夠很好地展示各區域價格受特征因子影響的程度，并給出影響的正負和穩定性。

研究使用了一個時間段跨度12個月的交易數據，分區域分析時樓盤個數偏少，不利于地理加權回歸分析工具的使用。研究也缺乏利用多時間段的交易和POI數據作對比分析，探索隨時間變化各特征因子對房價影響的改變。

從因素評價分析中發現，各區域高顯著性的特征因子互不相同，同一特征因子在不同區域顯著性和正負關系也不盡相同，說明各個區域樓盤的價格變化有其各自的原因和邏輯存在。這為細化調控政策的制定指出了方向，也就是“一區一策”。固然，在細化調控政策之前，需要結合研究結果進行實地調研，理解和認識各影響因子的作用機理，支持“一區一策”政策的制定。

參考文獻：

1.盧為民.建設促進上海房地產市場平穩健康發展的長效機制.科學發展.2018.07

2.李妍.數據分析在房屋交易中的應用.中國房地產.2019.31

3.崔光燦.促進上海房地產市場平穩健康發展長效機制研究.科學發展.2018.08

4.南寧市社會科學院課題組 王水蓮.供給側改革背景下房地產市場長效機制研究——以廣西南寧市為例.經濟研究參考.2018.59

5.張寅 何蕙 袁慶鋒.基于GIS和Mann-Kendall

方法的新增住宅面積趨勢分析.中國房地產.2017.36

6.邵琪.武漢市三環線內商品住宅價格空間特征及其趨勢研究.湖北工業大學.2018

7.朱傳廣 唐焱 吳群.基于Hedonic模型的城市住宅地價影響因素研究——以南京市為例.地域研究與開發.2014.33 （03）

8.陳真.福州市住宅價格空間分布特征及其影響因素研究.福州大學.2015

9.王洋 李強 王少劍 秦靜.揚州市住宅價格空間分異的影響因素與驅動機制.地理科學進展.2014.33 （03）

10.李文慧.蘭州市商品住宅價格空間分異及影響因素研究.蘭州交通大學.2017

11.李佳蔚.北京市住宅地價空間分異特點及影響因素研究.首都經濟貿易大學.2018

12.劉玲妙 劉建華 喬紅芳.我國房地產價格影響因素的區域差異——基于空間計量分析.閩南師范大學學報（哲學社會科學版）.2018.32 （04）

13.袁建林 趙春蘭.基于動態面板數據的房地產價格空間自回歸估算.遼寧工業大學學報（自然科學版） .2019.39 （02）

14.宋偉軒 劉春卉.長三角一體化區域城市商品住宅價格分異機理研究.地理研究.2018.37 （01）

15.周小平 秦振揚 趙松 柴鐸.中國住宅地價房價比的空間格局、演變特征及影響因素——基于35個大中城市的空間計量分析.中國土地科學.

2019.33 （01）

16.張明.基于ArcGIS的西安市住宅價格空間分布特征及影響因素研究.西安建筑科技大學.2018

17.張羽鶴.基于GWR模型的北京市二手房價格空間分異及影響因素研究.中國地質大學（北京）.2018

18.葛丹華.大連市商品住宅價格空間分異及其影響因素研究.遼寧師范大學.2017

19.尤修成.空間Hedonic模型二手房住宅價格研究.江西財經大學.2019

20.張景奇 史文寶 修春亮.POI數據在中國城市研究中的應用.地理科學.2021.41 （01）

21.薛冰 肖驍 李京忠 謝瀟 任婉俠 逯承鵬 姜璐.基于POI大數據的老工業區房價影響因素空間分異與實證.人文地理.2019.34 （04）

22.劉亞男.基于多源數據的城市房價空間分布特征及影響因素研究.西南大學.2019

23.薛冰 肖驍 李京忠 謝瀟 逯承鵬 任婉俠.基于POI大數據的沈陽市住宅與零售業空間關聯分析.地理科學.2019.39 （03）

24.彭濤.成都市住宅價格空間分異及其影響因素研究.四川師范大學.2020

25.劉雅軒 陳彤.基于POI數據的烏魯木齊市城市公園綠地對周邊住宅價格的影響研究.干旱區資源與環境.2020.34（11）