古箏琴板的振動特性初探研究?

嵇建書 裴永超 羅 敏 盧曉杰 鄭梅生

（南京林業大學機械電子工程學院，江蘇 南京 210037）

木材是木質樂器的重要組成部分，樂器質量等級主要由木材的材質決定，因此材料的選擇對于樂器的制作至關重要。由于缺乏理論指導和科學手段，從業者在古箏等木質樂器的實際制作中，主要通過看、聽、敲、掂等主觀判斷方法進行篩選，因此不僅樂器質量得不到保障，同時也造成木材的不合理利用與浪費。據行業相關統計，用于生產樂器共鳴板的原木出材率為10%～20%，出材率較低[1]。有研究表明，通過木材振動試驗，分析各類木材的振動特性，將木材振動與聲學聯系起來，有助于發現木材振動特性與木質樂器質量之間的關系，從而幫助生產廠家篩選、分類材料，提高我國的樂器生產制造水平和木材的利用率[2-5]。為此，本文以古箏琴板為例，通過理論與試驗分析相結合對木制樂器板材的振動特性進行研究，以期為古箏琴板及其他樂器木質板材的篩選與生產提供了一種有效的科學手段。

1 古箏琴板振動特性理論分析

木制樂器構造各異，但發聲原理基本相同。以古箏為例，其結構如圖1所示。木制樂器的初始振動由弦引起,琴弦振動導致面板振動，弦聲通過面板、背板等形成的共鳴箱放大并傳播出去,從而使人們享受到美妙的音樂[6]。

圖1 古箏結構Fig. 1 Guzheng structure

我國民族樂器共振板的材料主要為泡桐與云杉屬木材等[7-9]。共振面板是彈撥類樂器中的一個重要構件。琴板在振動時，既有彎曲振動，又有扭轉振動。本文首先對琴板振動特性進行理論分析，以求出振動的固有頻率理論解，為后續琴板振動試驗提供理論依據。

1.1 彈性體的彎曲振動

勻質彈性體如矩形截面梁在xy平面內作橫向彎曲振動，如圖2所示。設其長度為l，橫截面面積為A，ρ為每單位體積的質量，EI為彎曲剛度且為常量[10-11]。

圖2 板的受力分析Fig. 2 Force analysis of board

從中取一個長度為dx的微段，上面有剪力Q(x,t)、彎矩M(x,t) ，在任何時間t,其橫向位移可表示為y=(x,t)。忽略轉動慣量和剪切變形的影響，由圖3可知微段沿y方向力的平衡關系為：

圖3 板的微段受力分析Fig. 3 Force analysis of micro segment of board

解得其前5個值如表1所示。

表1 頻率方程解Tab.1 Solution of frequency equation

最后，得到彈性體的彎曲振動固有頻率計算公式如下[7]：

琴板屬于彈性體，因為是各向異性材料，如以板的振動研究會使問題復雜化。因此嘗試用公式（8）計算琴板的彎曲振動固有頻率，并進行試驗驗證。將琴板的基本參數代入式（8），得到其彎曲振動固有頻率f(Hz)近似計算公式如下[12]：

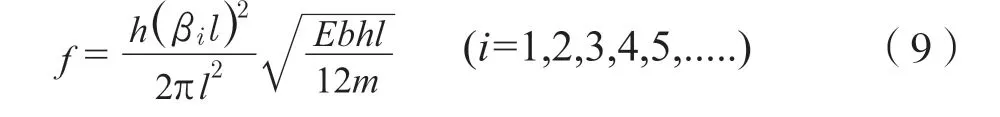
本試驗用古箏琴板材質為泡桐，長l=1.7 m，寬b=0.355 m，厚h=0.01 m，質量m=1.62 kg，泊松比μ=0.4，彈性模量E=5.8×109Pa[9]。將具體數值代入公式（9），解得該琴板前五階彎曲固有頻率如表2所示。

表2 琴板彎曲振動固有頻率Tab.2 Natural frequency of bending vibration of the board

1.2 彈性體的扭轉振動

勻質彈性體如等直桿繞x軸作扭轉振動，如圖4所示。設桿的截面抗扭剛度、抗扭常數和剪切彈性模量分別為GJt(x)、Jt(x)和G[13]。

圖4 桿的受力分析Fig. 4 Force analysis of the rod

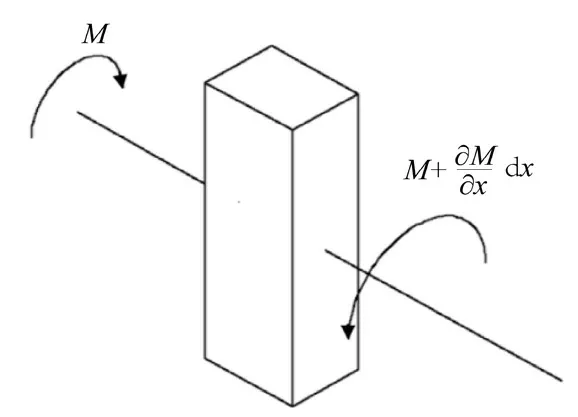
圖5 桿的微段受力分析Fig. 5 Force analysis of micro-segment of rod

假設桿扭轉振動時，截面的翹曲可忽略。在平面內，截面將保持繞x軸作微擺動[14],取微段dx，x截面的角位移表示為θ(x,t)，微段對x軸的轉動慣量Ip(x)，圓截面的極慣性矩為Jp。根據力矩平衡關系得[15]：

然后由邊界條件解得β值及振型函數H(x) ,最后得到板的扭轉振動固有頻率計算公式如下：

與琴板彎曲振動同理，嘗試用公式（14）計算琴板的扭轉振動固有頻率，并進行試驗驗證。將琴板的基本參數代入式（14），得到其扭轉振動固有頻率f(Hz)近似計算公式如下：

本文試驗用古箏琴板的剪切彈性模量G=2.07×109Pa，其他數值同上。將具體數值代入公式（15），解得該琴板的扭轉固有頻率如表3所示。

表3 琴板扭轉振動固有頻率Tab.3 Natural frequency of torsional vibration of the board

1.3 有阻尼系統的衰減振動

自由振動物體的定義為，振動的振幅是恒定的，振動將無限期地繼續下去。然而，實際的運動并非如此。自由振動的物體不但受到恢復力的作用，還受到阻力的作用，振幅會隨著時間逐漸衰減，最終趨于零并停止振動，如圖6所示[17]，其振動函數如下：

圖6 阻尼振動運動圖Fig. 6 Damping vibration motion diagram

通常把對振動過程的阻力稱為阻尼，阻尼大小取決于物體的形狀、尺寸及介質性質。琴板振動過程受阻尼的影響，呈現衰減振動。該分析結果將為試驗結果分析中的時域圖篩選提供一定的理論依據。

1.4 轉動慣量、剪切變形對板振動的影響

當板的橫截面尺寸與長度之比不是很小，或者在分析高階振型時，整個板被節點平面分成若干比較短的小段，這時需要考慮轉動慣量和剪切變形的影響[18]。該板的受力分析圖如下：

圖7 鐵木辛柯梁單元體受力圖Fig. 7 Force diagram of Timoshenko beam element

取微單元dx，繪制剪切力和彎矩引起的變形。在剪力為零的條件下，單元體dx的中心線垂直于橫截面。ψ為截面彎矩引起的夾角，β為剪力引起的剪切角，梁的軸線由彎矩和剪力引起的實際夾角為θ。通過建立動力方程、運動方程并求解，可得固有頻率pi(Hz)計算公式如下：

式（18）中p0(Hz)為不計轉動慣量和剪切變形影響下的固有頻率：

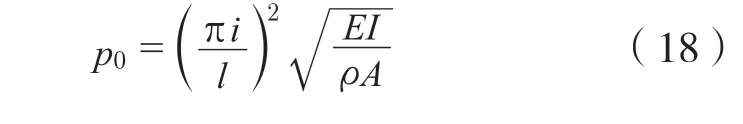
k為截面常數，矩形截面k=1.2，圓形截面k=1.11；EI為彎曲剛度，N·m2[10-11]；G為剪切彈性模量，Pa；ρ為每單位體積的質量，kg/m3；A為橫截面面積，m2。

由式（18）可知，考慮了剪切變形和轉動慣量后，系統的固有頻率減小。由于系統的質量和剛度可以決定固有頻率，剪切變形和轉動慣量的影響不僅增加了系統的有效質量，而且降低了系統的有效剛度，導致固有頻率下降。這種影響對高階頻率更為明顯。

綜上所述，琴板的實際固有頻率要比理論計算的數值小。該分析結果將為試驗結果分析中的時域圖篩選提供一定的理論依據。

2 琴板振動特性試驗臺設計

2.1 設計目的與技術要求

設計并制作一種樂器木質板材振動特性測試裝置，用于測試古箏、吉他等樂器的木質板材振動頻率、彈性系數、阻尼系數等振動特性參數，為木質樂器生產廠家提供科學篩選板材的方法。

技術要求：1）板材懸吊后只限制其垂直向下自由移動，懸掛位置為手動操作，有限位裝置； 2）支撐件位置可調，可以測試各類不同規格樂器板材及其他物體的振動特性；3）傳感器等測試元件位置、角度可調，裝夾方便；4）試驗臺易拆裝。

2.2 試驗臺整體結構設計

琴板測試臺由底板、立柱、掛棍、擋銷、橫梁、傳感器、傳感器夾、傳感器支撐架等構成（圖8）。底板用于支撐其他構件，其上開有橫、豎兩個方向的T型槽；兩根立柱及橫梁用于懸掛被測板材或其他物體，橫梁與立柱之間用G型夾固定；立柱可沿底板的T型槽作縱向移動與固定，方便測量不同大小板材；兩個支撐架外側均設有掛棍與擋銷，擋銷設置在掛棍上方，同時掛棍上設有凹槽懸掛試驗板材。傳感器支撐架可沿底板的T型槽作橫向移動與固定，方便傳感器靠近被測物體以接收信號；磁性表座安于傳感器支撐架上，并可快速固定；傳感器裝于磁性表座上，位置、角度均可調，裝夾方便；整個試驗臺易拆裝[19]。

圖8 試驗臺整體結構三維圖Fig. 8 3D drawing of the overall structure of the test bench

3 琴板振動特性試驗與結果分析

3.1 琴板自由振動頻率測試試驗

3.1.1 設備

自由振動試驗設備均購于北京東方振動噪聲研究所，包括振動分析軟件DASP-V11、云智慧采集分析儀INV3062、聲壓傳感器INV9206、力錘、電荷放大器、電腦、試驗臺等[20-22]。試驗系統如圖9所示。

圖9 自由振動試驗系統Fig.9 Free vibration test system

3.1.2 試驗方法

利用試驗臺將琴板懸吊，吊線選在節線位置；將聲壓傳感器的信號接收端固定于距離琴板中間3～5 cm處，接口端通過數據線與采集儀的2號端口連接；力錘通過電荷放大器與采集儀的1號端口連接；設置DASP軟件的初始環境；進行錘擊測試，錘擊位置不固定，力錘對每個被測位置依次進行3次敲擊，振動信號通過聲壓傳感器傳至采集儀，由采集儀將數據傳輸至振動分析系統進行處理。所有試驗室溫均為25 ℃，濕度為50%。

3.1.3 結果與分析[23-25]

經過振動分析系統處理后的時域圖如圖10所示，對應的頻譜圖如圖11所示，數據列表如表4所示。

圖10 時域圖Fig. 10 Time domain diagram

圖11 頻譜圖Fig. 11 Spectrum diagram

表4 數據列表(幅值譜Peak)Tab.4 Data list (Amplitude spectrum Peak)

由圖10、11可見，時域信號呈現典型的有阻尼衰減振動規律，頻譜圖的極值較為明顯，試驗結果較好。幅值譜的頻率數據，部分為琴板的彎曲振動固有頻率，部分為琴板扭轉振動固有頻率，其他為環境噪聲產生的干擾頻率。

3.2 琴板振動模態試驗

模態試驗是對古箏琴板振型進行試驗分析。力錘錘擊琴板時，3個加速度傳感器將振動信號傳遞至采集儀，由其將信號傳遞至振動分析系統，采用模態與動力學分析模塊進行模態分析。

3.2.1 彎曲振型

1）主要試驗設備同3.1.1所列。

2）試驗方法

首先用2塊海綿支撐試驗用琴板，與力錘連接的電荷放大器和3個加速度傳感器依次分別接入采集儀的1至4號通道，3個加速度傳感器分別置于選定的被測點，并用雙面膠將其固定于琴板上；設置DASP軟件內的信號采集模塊，對錘擊試驗進行預試驗，用力錘在每個被測點依次進行3次敲擊，通過軟件內的顯示情況，判斷預試驗是否良好，若正常再進行正式試驗。

3）結果與分析

試驗得到的數據為時域信號。首先從時域圖中選取一組信號良好的試驗數據，利用振動分析系統中的模態與動力學分析模塊對數據進行分析計算，操作步驟依次為數據導入、參數設置、頻響函數計算、琴板結構生成、輸入約束、脈沖響應函數、特征系統實現算法等，最后得到古箏琴板彎曲振動的前五階固有頻率、阻尼比（表5）及部分振型（圖12、13）。

表5 彎曲振型固有頻率和阻尼比Tab.5 Bending mode natural frequency and damping

圖12 琴板彎曲二階模態振型圖Fig. 12 Second order modal diagram of the board bending

圖13 琴板彎曲三階模態振型圖Fig. 13 Third order modal diagram of the board bending

二階模態振型主要表現為琴板凹陷與凸起的往復運動。三階模態振型主要表現為從左側起凸起、凹陷、凸起以及凹陷、凸起、凹陷的交替運動。通過對比觀察彎曲振型的固有頻率和自由振動的頻率大小，可以在表4中找到與表5相近的頻率，再結合理論計算固有頻率值，整理獲得柱形圖14。

圖14 彎曲振型固有頻率與自由振動頻率以及理論計算固有頻率對比Fig.14 Comparison of natural frequency of bending mode and free vibration frequency and theoretical calculation natural frequency

對比圖14中彎曲振型固有頻率和自由振動頻率以及理論計算所得出的前五階頻率，發現各階頻率值均相近，平均誤差在5%以內，表明本文的研究結果可信度較高。

3.2.2 扭轉振型

1）主要試驗設備同3.1.1所列。

2）試驗方法

首先進行DASP軟件的設置，根據采樣頻率約為試驗結果最高頻率的5倍的試驗要求，選用采樣頻率為2 048 Hz；試驗采用4個通道，第1個為力錘通道，其他3個為加速度通道，設置每個通道的標定值；試驗為錘擊試驗，觸發次數為3次，采樣點數為采樣頻率數值的一半，即1 024個，觸發力設置為10 N；進行示波與零點平衡校準。然后將琴板兩端放在備好的2塊海綿上，避開一階扭轉的節線位置，將加速度傳感器依次放在選定的被測點，并用雙面膠將其固定；在琴板上依次選取7個激勵點，力錘對每個激勵點進行連續3次敲擊，并采集試驗信號。

3）結果與分析

加速度傳感器將信號傳遞至分析儀進行處理，在振動分析系統中顯示為時域信號，然后對時域信號進行篩選，選用模態與動力學分析模塊依次進行分析，最后通過該模塊的脈沖響應函數分析和特征系統實現算法得到琴板扭轉振動的前五階固有頻率、阻尼比（表6）及部分振型。

表6 扭轉振型固有頻率和阻尼比Tab.6 Torsional mode natural frequency and damping ratio

圖15 琴板扭轉二階模態振型圖Fig. 15 Second-order mode shape of torsional vibration of the board

圖16 琴板扭轉三階模態振型圖Fig. 16 Third-order mode shape of torsional vibration of the board

通過對比觀察扭轉振型的固有頻率和自由振動的頻率大小，可以在表4中找到與表6相近的頻率，再結合理論計算固有頻率值，整理得到柱形圖17。

對比圖17中扭轉振型固有頻率和自由振動頻率以及理論計算所得出的前五階頻率，發現各階頻率的值均相近，平均誤差在6%以內，表明本研究具有較高的可信度。

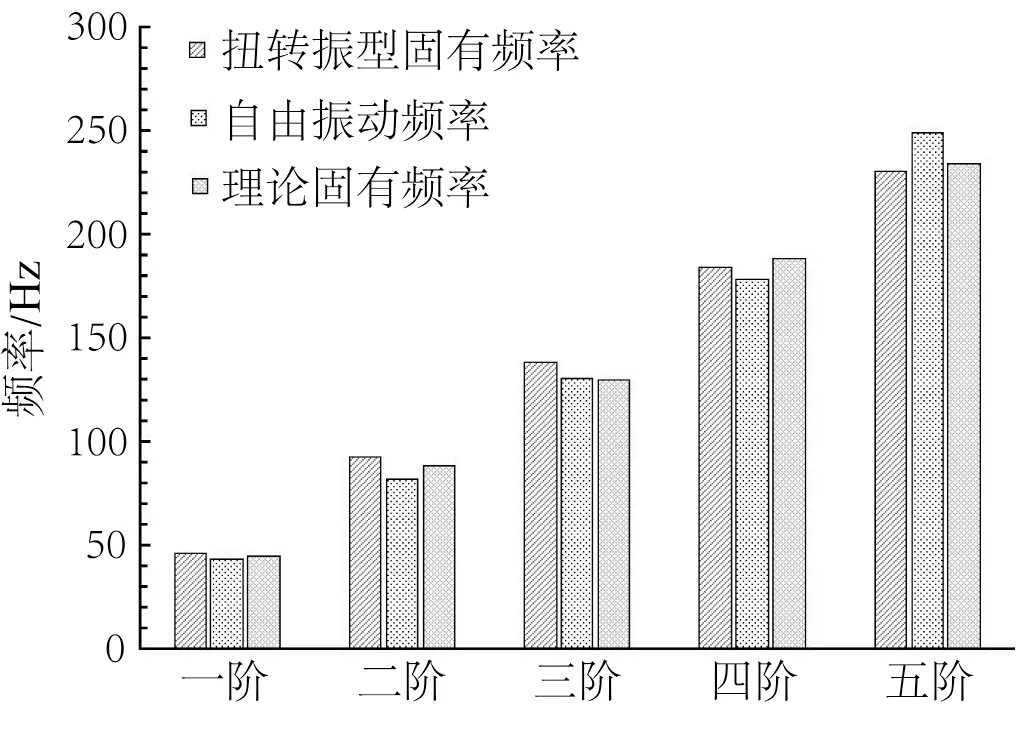
圖17 扭轉振型固有頻率和自由振動頻率以及理論計算固有頻率對比Fig.17 Comparison of natural frequency of torsional mode and free vibration frequency and theoretical calculation natural frequency

4 結論

本文以古箏為例研究了樂器木質板材振動特性，對古箏琴板彎曲振動和扭轉振動進行了理論分析和有阻尼的衰減振動分析，得到琴板的彎曲和扭轉振動的前五階固有頻率理論計算值；設計并加工制作試驗臺；分別利用聲壓傳感器和加速度傳感器進行了琴板的自由振動頻率測試與彎曲和扭轉振動模態試驗，獲得琴板自由振動頻率試驗值及其彎曲和扭轉振動前五階固有頻率試驗值及振型；琴板振動的理論計算結果和2種試驗結果對比表明：3個數值大小相近，平均誤差分別在5%及6%以內，驗證了本文試驗方法的可行性和試驗數據的可信度。

該研究成果對今后廠家篩選樂器木質板材具有一定的指導意義。今后還需深入研究樂器聲學品質與木材振動性能的關系，并結合使用者對樂器成品的主觀評價，綜合分析，才能客觀、科學地選取理想的樂器木質板材。