面向動態負載的集群容器部署方法

尹 飛，龍玲莉，孔 崢，邵 涵，李 鑫，錢柱中

（1.江蘇方天電力技術有限公司，南京 211102；2.南京大學計算機科學與技術系，南京 210023；3.南京航空航天大學計算機科學與技術學院，南京 211106）

（?通信作者電子郵箱lics@nuaa.edu.cn）

0 引言

數據中心與集群以云計算的形式，根據用戶動態的資源需求變化，“按需式”地為其提供可配置的資源獲取服務，以實現索取資源的彈性伸縮，涵蓋了傳統的基礎設施即服務（Infrastructure as a Service，IaaS）［1］、平臺即服務（Platform as a Service，PaaS）［2］與新興的無服務計算［3］等。這些服務模型的支撐在于基于容器化［4］的資源管理技術，以容器為上層應用提供相互隔離的計算資源。

為了應對大規模用戶的訪問請求，同種應用功能的多個運行實例往往被各自獨立地部署于預先創建的容器之中［5］。繼而，為了提升宿主機（承載容器的物理機）資源利用率，同時降低多個容器實例間的通信開銷，容器會被整合到少量宿主機之上［6-7］。這樣“緊致”的部署，能夠在滿足應用服務的同時，極大提升集群的資源利用率。

不僅如此，在運行過程中，應用的負載往往是動態變化的，文獻［8-10］表明集群內各類應用的請求訪問量在時間上的分布不均，如:淘寶在“雙十一”期間的訪問量會劇增；假期時社交網站的照片分享量會極大超出平時的均值水平；新聞事件也會使得應用的瀏覽量產生大幅度的波動。為此，集群更需要根據應用的負載變化，動態調整容器的資源配置，以滿足應用業務的服務質量。

然而，為了整合宿主機資源［11-15］，現有的工作主要從按需式、被動式［16-18］的容器遷移入手。一方面，已有工作探討了在宿主機上進行共享資源使用過程中，容器之間產生的資源干擾［9，19］；另一方面，一些研究在結合了共享資源使用特點［8，20］的基礎上，進行容器整合的策略制定，提升宿主機的資源利用率。雖然也有工作通過預測及刻畫應用各異的資源需求［21-22］，幫助容器進行更好的整合，但這些工作均帶有較強的輸入分布假設。

即使現有的容器化技術已經能較好地支持“應對式”的資源彈性伸縮和配置，但是對于動態負載來說，在線化的配置需求增加了作出合理容器部署的難度。一個簡單的例子是，短期內“近乎完美”的容器整合可能造成未來更多容器熱遷移。也就是，當容器負載過高而宿主機沒有空閑資源進行拓展時，容器不得不采取熱遷移的方式，將實例轉移至其他空閑服務器。隨之而來，熱遷移不僅消耗大量計算與網絡資源［23］，也會增加應用響應時間，對服務質量產生較大的影響。

結合針對集群負載的長期觀察，容器的資源需求往往是此消彼長。如果能將這些此消彼長的容器整合在一臺宿主機上，那么容器將會以較小的概率同時具有資源擴展需求。因此，只需為每一臺宿主機預留少量資源，即可避免后續大部分的容器熱遷移。然而，如何將合適的容器整合宿主機上，并確定合適的資源預留量是關鍵，其直接影響了宿主機的資源利用率與容器的服務質量。

雖然容器的資源需求量在不斷變化，但是在彈性資源伸縮的時候，其申請增加或是釋放的資源量往往具有最小的變化單位，如一個CPU 核、1 GB 內存等。相較于傳統“非忙即閑”的資源模型，有限的資源使用狀態及其間的變化關系更能作為細粒度描述容器資源動態變化的依據。例如，聊天應用包含有文字、語音等多種媒介，以至于信息傳輸負載的呈現也僅在這幾個狀態間切換。

為此，本文首先以細粒度的方式刻畫容器的動態資源變化，即用馬爾可夫鏈中的狀態和狀態間的轉移，對應建模容器可能的資源需求量和不同資源需求量之間的切換。圖1 展示了一個具有3 種資源需求狀態的容器示例。然后，本文在基于資源預留的基礎上提出面向動態負載的容器部署問題，以在限定動態遷移概率的約束下，最小化宿主機的使用數量。本文提出了面向動態負載的容器部署策略，并通過估計容器資源需求，提高部署效率。大規模基于國產軟硬件的實驗結果表明，所提出的部署策略能在提高宿主機資源利用率和減少容器動態遷移次數間取得平衡，在長效時間上以至多26 臺宿主機的增加換取至多7次容器遷移。

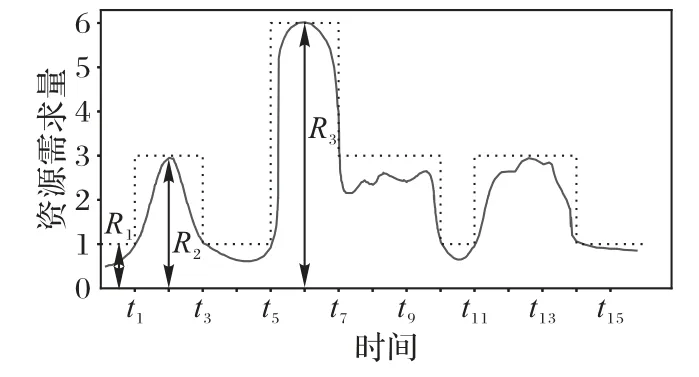
圖1 容器隨時間變化的資源需求Fig.1 Resource demand of dockers varying with time

本文的主要工作有:1）用馬爾可夫鏈建模容器的多狀態資源需求變化；2）提出面向多狀態負載的容器部署策略，利用資源需求量的估計值提高部署效率；3）進行大量實驗，通過與其他部署策略比較，評估本文所提出的部署策略的性能。

1 相關工作

1.1 虛擬機/容器負載刻畫

動態負載的變化是虛擬機/容器部署過程不可忽視的特征。由于容器是輕量級的虛擬機，因此，本文只考慮針對容器的相關部署與應用。文獻［8］統計了Google 集群中不同資源的利用率以及各自對應的總時間占比，表明了資源需求變化的動態性和可描述性；文獻［19］研究了負載激增的模式，提出有關激增負載測試的方法；文獻［9］調研了資源需求量波動對服務質量的影響；文獻［20］優化了數據中心與集群針對容器負載變化而產生的重配置資源的開銷。上述工作對資源配置的某方面開展了研究，但未考慮合理調整資源利用的方式。

近期工作主要致力于把變化的負載建模成為隨機變量，即非確定量。文獻［21］提供了在資源需求量服從特定隨機分布下的近似算法；文獻［22］主要研究了資源需求服從正態分布的情況；文獻［14-15］提出針對資源需求量服從高斯分布的近似算法。這些相關方法可以提供一定的資源需求描述能力，但難以支撐容器部署的穩定性要求，易引發容器遷移。

然而針對服從特定概率分布的資源需求量而設計的算法不具有普遍性。雖然文獻［24］把激增的資源需求量建模為二狀態馬爾可夫鏈，但該算法對資源需求量的狀態數等有較大限制。

1.2 虛擬機/容器整合與遷移

作為提高資源利用率的重要方式，虛擬機/容器整合［11，25］已被學術界和工業界廣泛地研究與認可。工業界代表性的產品有VMware 分布式資源調度［12］和IBM（International Business Machine）服務工具［13］。大多數研究把這個問題視作:在服務器容量、服務等級協議等限制條件下最小化所使用的物理服務器數量。這些工作均將容器資源需求量表示為定值，使用一系列類似裝箱的啟發式策略，如降序首次適應（First Fit Decreasing，FFD）［6］、隨機裝箱等［14-15］，卻無法應對集群環境中動態的容器資源變化需求。

當宿主機資源無法滿足容器資源擴張需求時，容器熱遷移隨即進行。文獻［16］以同時最小化遷移傳輸能耗及容器服務時延作為目標；文獻［17］旨在設計具有時延保障的熱遷移策略；另有文獻［18］考慮集群間利用傳輸控制協議（Transmission Control Protocol，TCP）的路徑多樣性進行熱遷移。但這類工作往往是被動地進行容器的調整，沒有在長效時間維度上進行容器整合與遷移的優化。

針對上述工作的局限，本文使用多狀態馬爾可夫鏈為容器的資源需求量變化進行建模，以設計有效的面向動態負載的容器部署策略。

2 系統模型

2.1 場景定義

集群有大量的物理機，通過在物理機（宿主機）上部署容器來向用戶提供服務。如圖2 所示，容器與宿主機的關系由部署策略決定。

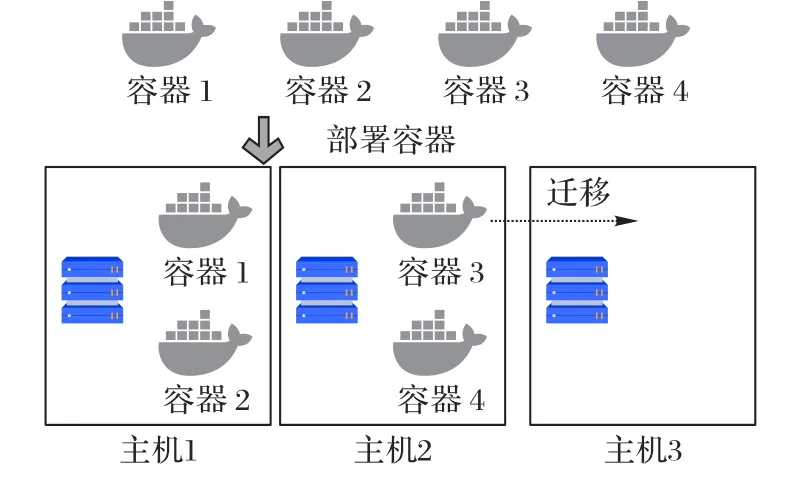
圖2 容器部署示意圖Fig.2 Schematic diagram of docker deployment

一方面，盡管用戶通常會聲明容器的最大資源需求量，但由于物理機的購置成本、維護成本和運行成本都較高，總是為每個容器預留足夠的計算資源在經濟上是不合理的。運營者總是希望盡可能減少宿主機的占用量。另一方面，若沒有為容器預留一定的計算資源，當其資源需求量發生變化時，集群必須通過動態遷移來保證容器的性能不受影響，由此會帶來較大的遷移代價。基于這兩點考慮，本文旨在為集群設計一種容器部署策略，使得宿主機資源利用率較高、數量較少，同時把容器動態遷移次數控制在較小的范圍內。

2.2 單容器資源需求模型

容器資源需求量是動態變化的，能被量化為多個狀態（如圖1 所示）。本文將該特性稱為容器的多狀態特性，并用多狀態的馬爾可夫鏈進行建模，如圖3所示。假設集群共創建了n臺容器，并考慮第k臺容器。用Nk表示第k臺容器的狀態總數，并令R(k)=(R1(k)，R2(k)，…，，其中Ri(k)表示第k臺容器中狀態i的資源需求大小。本文用Pij(k)表示第k臺容器中狀態i到狀態j的轉移概率，那么這些參數所構成的是這臺容器的狀態轉移概率矩陣。本文用Sij(k)表示第k臺容器在兩個連續時間段從狀態i轉換到狀態j的次數，那么有Pij(k)=以圖1 所示為例，分別用R1(k)、R2(k)、R3(k)表示由少到多的三種資源需求量，則S11(k)=2，S12(k)=2，S13(k)=1，且能計 算轉移 概率為P11(k)=0.4，P12(k)=0.4，P13(k)=0.2。

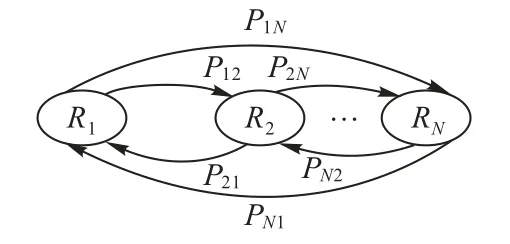
圖3 基于馬爾可夫鏈的容器資源狀態模型Fig.3 Markov chain based resource state model for docker

一般來說，上述描述的馬爾可夫鏈通常是非周期不可約的，因為實際應用中任兩個狀態都有可能相互切換。而任何狀態都可能在下一刻保持不變，故存在有平穩狀態的分布，即μ(k)=(μ1(k)，μ2(k)，…有:

因此，容器k的描述可由其資源需求量R(k)和平穩分布μ(k) 組成，構成的是2×n維矩陣，定義為V(k)=[R(k)，μ(k)]T，1 ≤k≤n。

2.3 多容器的復合資源需求模型

對于n臺容器來說，每個V(k)有Nk種狀態，每臺容器的狀態變化相互獨立。因此，這n臺容器一共有N=種狀態。用S(k)表示容器V(k)當前的所有狀態，則這n臺容器在當前的復合狀態可以用S=(S(1)，S(2)，…，S(n))來表示。那么，從狀態S轉移到S'=(S(1)'，S(2)'，…，S(n)')的概率為:

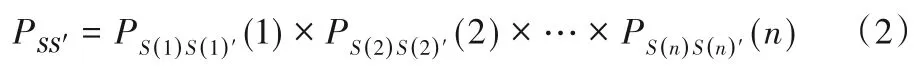
這里需要說明，本文將總共N種狀態用1～N進行標號。更進一步，對于當前所處的狀態(S(1)，S(2)，…，S(n))，本文用i1表示S(1)，i2表示S(2)，以此類推。從而有狀態轉移矩陣P=[Pij]N×N。這個馬爾可夫鏈通常也是無周期不可約，故存在唯一的可達的平穩分布:

根據2.2 節所述，容器V(k)的平穩分布定義為μ(k)=(μ1(k)，μ2(k)，…，μNk(k))。則π和μ(k)的關系如定理所述。

定理1令有π=π'，即n臺容器平穩處于某一狀態的概率等于所有容器各自平穩時處于對應狀態概率的乘積。

證明 因為πP=π解得的π是唯一的，所以只需要證明π'P=π'，即證也即:

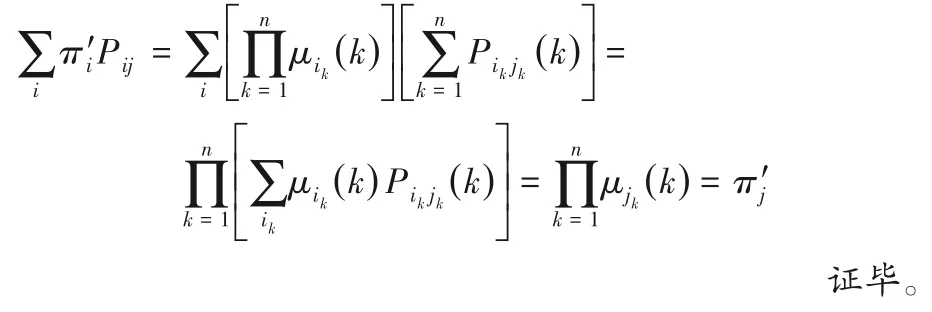
定理1 說明，在實際計算中，只需要預先算出每臺容器的平穩狀態分布，再進行簡單乘法運算就能得到n臺容器的平穩狀態分布。

2.4 動態負載容器的部署與資源預留問題

集群有m臺宿主機，第l臺宿主機Hl的可用資源可以用其容量Cl來描述，即Hl=Cl，1 ≤l≤m。容器的部署過程實際上是從容器到宿主機的一個映射過程，用矩陣X=來表示，當V(k)放置在Hl上時有Xkl=1，否則Xkl=0。

令W(k，t)表示容器V(k)在t時刻的資源需求量。理想情況下，所有宿主機在t時刻都能提供充足的計算資源。該約束條件可以表示為:

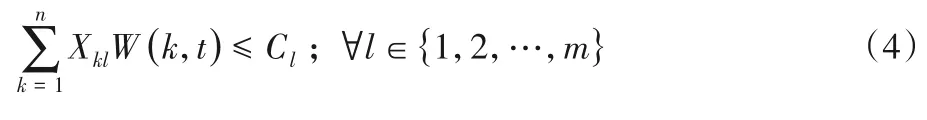
特別地，在初始時刻，即t=0 時，該約束滿足。如果在t時刻該約束被破壞，則定義為發生了一次沖突。用vio(l，t)表示Hl是否在t時刻沖突，即:

沖突率為長時間運行過程中發生沖突的時間占總時間的比率，宿主機Hl的沖突率為:

CVR越小意味著容器動態遷移的幾率越小。本文的策略目標是保證所有宿主機的沖突率保持在一個較低的值ρ以下，即使得:

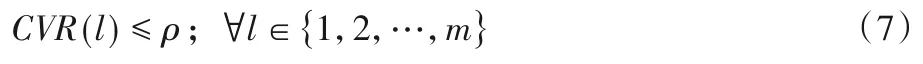
上述約束為宿主機的性能約束。下面給出面向動態負載的容器部署問題的定義。

定義1面向動態負載的容器部署問題是指，給出所有容器和宿主機參數V和H，找到一個從容器到宿主機的映射，使得在初始時刻滿足容量約束以及在任意時刻滿足性能約束的同時，總共使用的宿主機數量最少，也即:

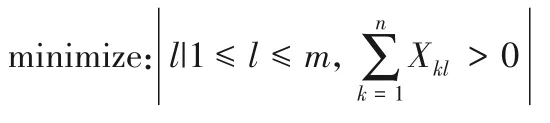
滿足容量約束（式（4）），當t=0 時；滿足性能約束（式（7）），對所有t。

定理2面向動態負載的容器部署是NP（Non Polinomial）完全的。

證明 通過將NP 完全的裝箱問題判定版本歸約到所提出的面向動態負載的容器部署問題的判定版本來完成定理證明。裝箱問題判定版本為:給定n個物品，第k個物品的大小是gk∈(0，1]，能否用m個單位容積箱子裝下物品？

對任意一個給定的裝箱問題判定版本實例，構造一個面向動態負載的容器部署問題（判定版）實例:令Nk為任意正整數，?k∈{1，2，…，n}；令Ri(k)=gk，?k，?i∈{1，2，…，Nk}；再令Cl=1，?l∈{1，2，…，m}；令ρ=0。這樣可在多項式時間內完成歸約，因此所提問題是NP完全的。 證畢。

3 面向動態負載的容器部署與資源預留

3.1 容器的資源預留策略

在單臺宿主機上部署n臺容器，這n臺容器一共有N個狀態，用Ri表示標號為i的狀態的資源需求。不失一般性，不妨設R1≤R2≤…≤RN，則可以導出這n臺容器最小所需容量Rq，其中q為滿足如下關系的整數:

此時的性能約束滿足:

根據式（8），判斷n臺容器能否同時放置在某臺宿主機l上的算法De(V，Hl)，具體描述見算法1 所示，其輸出為能否放置的結果。

算法1 宿主機能否容納容器（Determination）。

輸入 特定宿主機l，容器的馬爾可夫模型V={V(1)，V(2)，…，V(n)}；

輸出n臺容器能否放于特定宿主機l。

如果PI＞ρ，輸出0（否）；否則輸出1（是）。

3.2 面向動態負載的容器部署策略

現在考慮多臺宿主機的情況。將n臺容器部署到m臺宿主機上，基于FFD 啟發式算法設計部署策略，將n臺容器按資源需求量的期望R(k)·μ(k)降序排序，并將m臺容器按其容量降序排序。對給定的一個容器，依次嘗試每個宿主機，若當前宿主機滿足約束條件，則將容器部署在該宿主機上，否則嘗試下一個宿主機直到這臺容器被部署成功。算法MultiCons（n，m，d，V，H）的具體描述見算法2 所示，其中向量H包含所有可用的宿主機，d為單個宿主機上所能允許部署的最大容器數量。

記Nmax為n臺容器各自的狀態數的最大值，即Nmax=maxNk(1 ≤k≤n)。容器排序時間復雜度為O(nlbn)，宿主機排序復雜度為O(mlbm)，部署一臺容器的復雜度為部署n臺的復雜度為而容器部署算法總的復雜度由部署時間所決定，即Nmax一般是比較小的常數，d是確定的整數，故只是一個系數，算法的復雜度為O(nm)。然而，當實際運行中nm的規模不夠大時是一個相當大的系數，直接導致部署時間延長。為了縮短部署時間，在3.3 節將提出一種估算最小資源預留量的預判方法。

算法2 面向動態負載的容器部署（MultiCons）。

輸入 容器總數n，宿主機總數m；單宿主機允許部署最大容器數d；容器的馬爾可夫模型V={V(1)，V(2)，…，V(n)}；宿主機模型H={H1，H2，…，Hm}。

輸出 容器到宿主機的映射X=

3.3 面向動態負載的容器部署加速

在算法2 中，如果前面l臺宿主機上已經部署了比較多（不妨假設為d-1臺）容器，其將不再容納任何有較大資源需求的其他容器。但算法2 在部署一臺明顯無法放置在這l臺宿主機上的容器時，仍需要從第一臺宿主機開始嘗試，直到付出了的代價，才判斷出前l臺宿主機都無法容納。顯然，這種情況是對計算的極大浪費。本文考慮尋找一個可以簡單計算出的參數，來判斷容器是否有很大概率無法部署在特定宿主機上。本文先考慮所有容器的資源需求為獨立的二項分布，如表1所示。

表1 容器的資源分布Tab.1 Resource distribution of dockers

正態分布的累積概率為Fz(zα)=P(Z≤zα)=1-α。現有一臺宿主機上已部署k臺容器，需要判斷第k+1 臺容器能否部署在該宿主機上。用X表示這k+1 臺容器的總資源需求量，即X=X1+X2+…+Xk+1，根據中心極限定理，有:

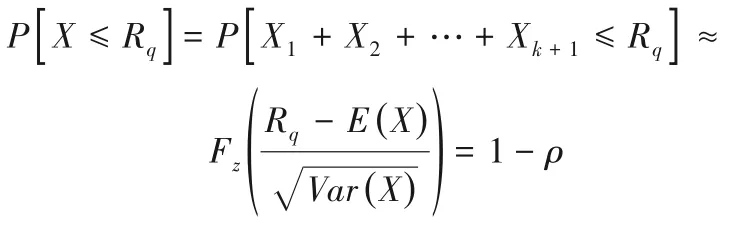
本文分別用Xmin、Xmax表示Xk的最小值和最大值，進而得到:

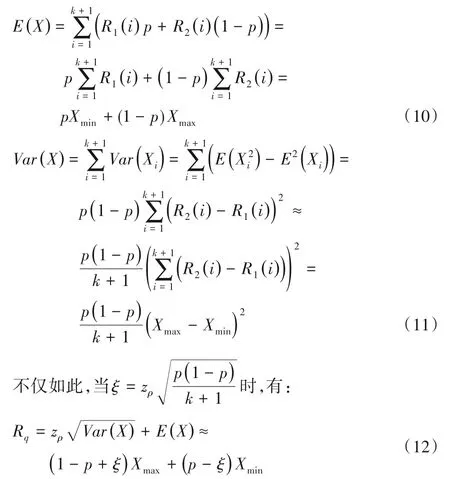
當Rq＞Hl時，可以判斷第k+1 臺容器無法放置在宿主機l上。這里Rq的計算有兩個假定:1）所有的容器服從相似的概率分布。由于FFD將所有容器按照其資源需求量的期望排序，所以放置在同一臺宿主機上的大多數容器具有相似的期望。在實際情況下，可以將容器按分布聚簇，再排序部署，使其更加準確。2）所有容器都是二狀態的。在實際情況中，容器狀態數會大于2，Xmax會導致實際結果偏大，在Xmax前加上修正α，得:

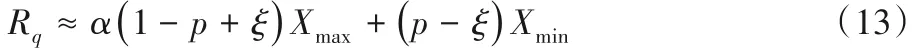
對于修正系數α，可以利用容器的分布估算。先考慮只有一臺的情況:對于二狀態的容器，易知α=1。對于N狀態的容器(N≥3)有:

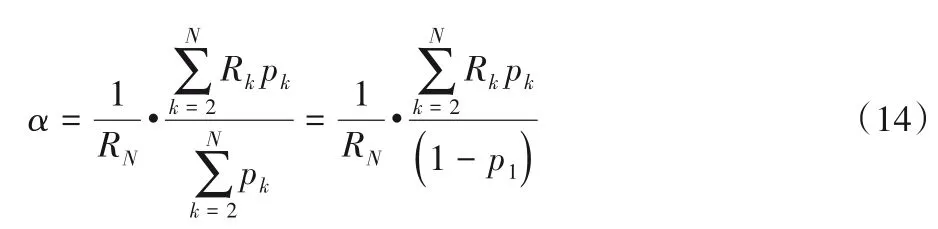
當有n臺容器具有不一樣的狀態數時，有:

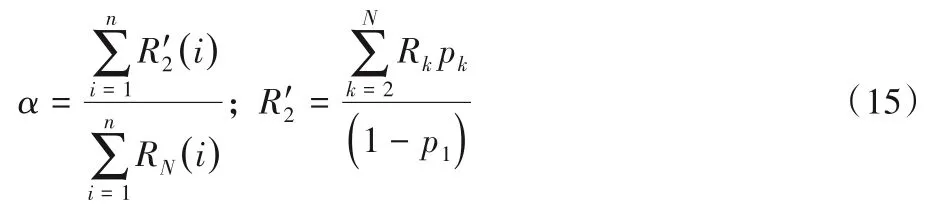
以式（14）、（15）計算出的α作為參考值，若在當前α下算法運行結果準確率比較低時，可以通過減小α來提高準確率；當運行時間較長且準確率較高時，可以通過增大α來縮短運行時間。據此，提出面向動態負載的容器加速部署策略（如算法3 所示），該算法能夠結合宿主機和容器各自不同的狀態進行動態部署。

這里提出用中心極限定理估算Rq方法的合理性在于:一般來說，若n≥9×max中心極限定理就可以得到較好的擬合效果。在實際的部署中，當容器的數量比較小時，資源需求量和計算出的Rq都遠小于H，所以估算效果的好壞不影響結果；但當容器的數量比較大時，這種方法的估算效果好，得到比較準確的結果。

算法3 容器的加速部署（QuickMultiCons）。

輸入 容器總數n；宿主機總數m；單宿主機允許部署最大容器數d；容器的馬爾可夫模型V={V(1)，V(2)，…，V(n)}；宿主機模型H={H1，H2，…，Hm}。

4 實驗與結果分析

4.1 實驗概述

為驗證部署策略的有效性，在基于國產軟硬件環境的基礎上，結合開源系統，設計了一系列實驗，驗證不同參數配置下所提設計算法的效果。

4.1.1 測試床環境

基于國產軟硬件環境及開源系統，本文部署并測試環境運行的可行性。主要實驗環境配置及具體參數包括:測試床服務器為浪潮SN5160M4（IntelE5-2680V4 CPU*2、256 GB（8*32 GB RDIMMG）DDR4 內存、1.2 TB 熱插拔SAS 硬盤2.5"*6）；系統為中標麒麟（kernel-2.6.32；KVM-0.12）；資源管理系統為OpenStack R版本；語言環境為Python 3.8。

4.1.2 對比算法

在測試床的基礎上，通過模擬程序行為實現了所提容器部署策略MULTI（MULTIple），并與三種常用的容器部署策略進行了比較:1）按谷值配置容器的策略RV（Resource with Valley）；2）按峰值配置容器的策略RP（Resource with Peak）；3）按谷值峰值的平均配置容器的策略RVP（Resource with Valley and Peak）。三種部署策略也都使用了FFD策略。在部署完成后，按照真實容器的分布，產生1 000 組實時數據進行仿真，出現沖突時測試床將容器動態遷移到其余空閑宿主機，記錄運行性能結果。

4.1.3 驗證指標

衡量部署策略的性能的參數包括部署一定臺數容器所需的宿主機數（Physical Machines，PM）、沖突率（Capacity Violation Rate，CVR）和動態遷移次數（MIGration，MIG），其中PM、CVR、MIG分別是1 000組數據產生宿主機數目的最大值、沖突率平均值、動態遷移次數最大值。

4.1.4 實驗參數

實驗涉及的參數包括:容器數量（VM）、容器資源需求相對大小（R1∶R2∶…）、容器資源需求的平穩分布概率（P1∶P2∶…）、容器資源需求量的絕對大小（Rmean=宿主機容量（H）、宿主機允許的最大容器數（d）以及宿主機的性能約束（ρ）。

實驗主要驗證容器資源需求的分布區間（R1∶R2∶…）、絕對大小Rmean和平穩分布（P1∶P2∶…）在不同配置下對部署效果的影響，得到部署策略最優的參數配置范圍。實驗中容器有50%概率為二狀態，50%概率為三狀態。宿主機的容量H為（80，100）的均勻分布，d設為16，ρ設為0.04。三狀態容器和二狀態容器的資源需求量平穩分布分別如表2和表3所示，容器資源需求量分布如表4 所示。表2 的含義是對每一臺容器，其P1在0～P內等概率隨機取值，P2在0～(1-P1)內等概率隨機取值，P3取1-P1-P2。表3和表4的含義類似。

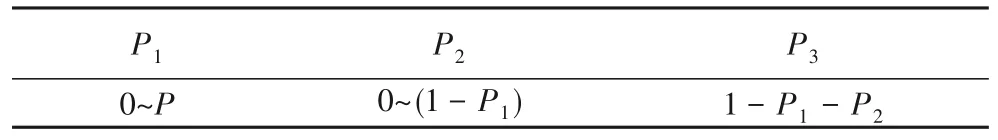
表2 三狀態容器的資源需求量平穩分布Tab.2 Resource demand stationary distribution of dockers with three states

表3 二狀態容器的資源需求量平穩分布Tab.3 Resource demand stationary distribution of dockers with two states

表4 容器資源需求量分布Tab.4 Distribution of docker resource demand

累計進行了4組綜合實驗:

1）調節容器資源需求量的絕對大小:固定P=1，R分別取3～7，從而改變Rmean。

2）調節容器資源需求的平穩分布概率:分別在P等于0.2、0.4、0.6、0.8、1.0的情況下進行實驗，并通過改變R固定Rmean=6.125。

3）調節容器資源需求的分布區間:固定P=1 和Rmean=6.125，改變R值調節容器資源需求。

4）部署策略運行的時間代價:取P=1和R=5，將10 000臺容器分成100批，每批100臺，按批次進行部署，并記錄下每批容器部署的時間。

4.2 模擬實驗結果

實驗1 的結果如表5～6、圖4 所示。RV 使用最少的宿主機，動態遷移次數最多。RP 動態遷移為零，使用的宿主機最多。RVP使用較少的宿主機，但動態遷移次數較多，沖突率會隨容器條件的變化而產生較大起伏。MULTI 使用少于RP 的宿主機數，并且保持較少的遷移次數和較小沖突率。RV 與RVP 在R＜5 時的沖突率很小，R≥5 時更能體現MULTI 算法的性能效果。在現實中，一般宿主機上都會布置10 臺以上容器［24］，所以模擬實驗的結果在R=5 時更貼近真實的情況。隨著R增大，MULTI 的PM增長速度大于RVP 的PM增長速度，這是因為R增大會導致單臺宿主機上放置容器數量減少，即式（10）的k減小，得到更大的Rq。

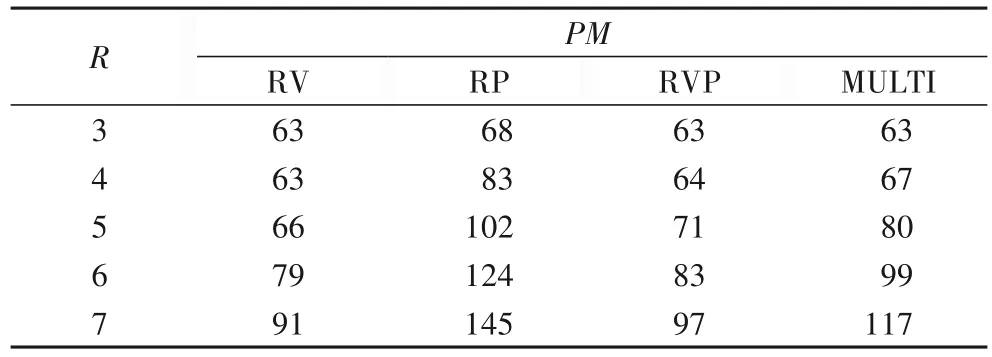
表5 PM與R的關系Tab.5 Relationship between PM and R

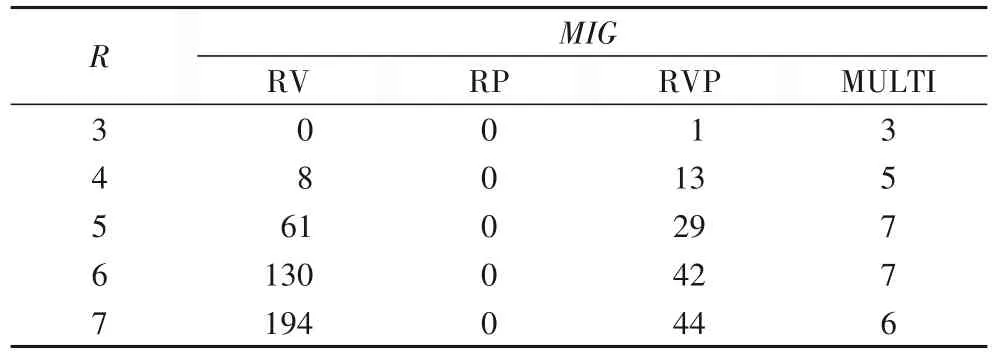
表6 MIG與R的關系Tab.6 Relationship between MIG and R

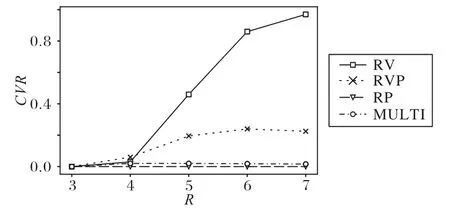
圖4 CVR與R的關系Fig.4 Relationship between CVR and R

實驗2的結果如表7～8、圖5所示。隨著P的增大，MULTI策略下的PM略有增大，但幅度比較小。增大的原因是:根據式（10）、（12），資源預留量Rq與容器資源需求的期望和方差有關，當保持Rmean恒定時，Rq的大小由容器資源需求的方差大小決定，經過簡單計算可知基于表4的分布，P越大，容器資源需求的方差也越大，所需要的資源預留量越大，進而所使用的宿主機數量越多。RV、RP、RVP 三種算法的PM增大是因為R的增大。RV、RVP 的MIG和CVR都相當地大且不穩定，MULTI 的MIG一直保持在較小數值7，CVR也均保持在0.04以下，意味著當容器需要資源擴張的時候，其與宿主機的沖突率一直保持較低水平，也能夠體現在宿主機上提前預留資源的好處。

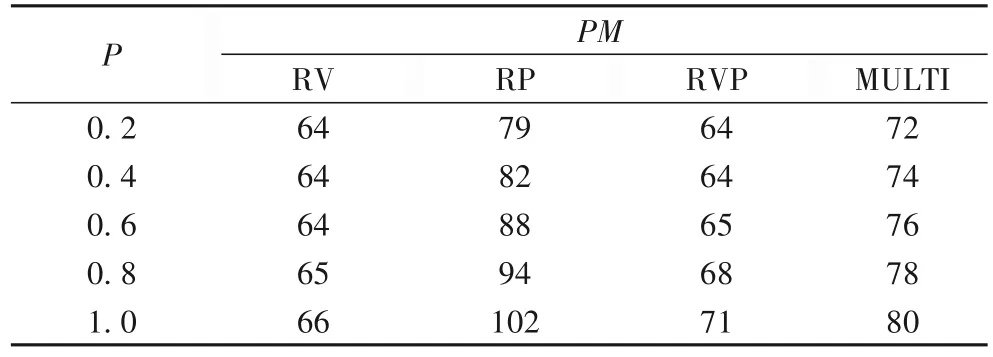
表7 PM與P的關系Tab.7 Relationship between PM and P

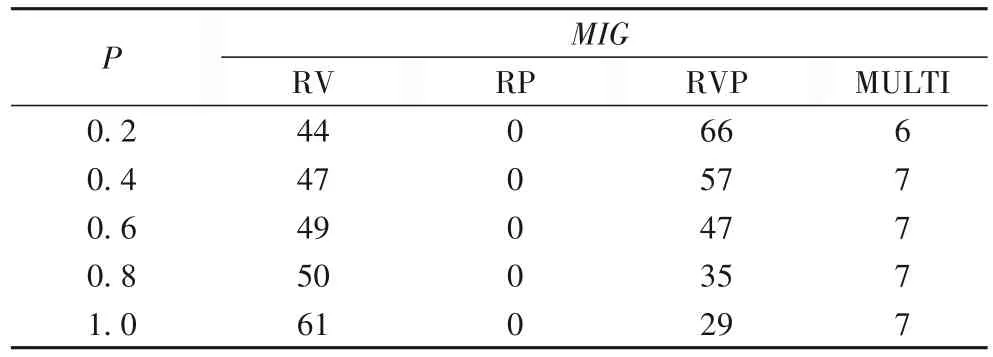
表8 MIG與P的關系Tab.8 Relationship between MIG and P

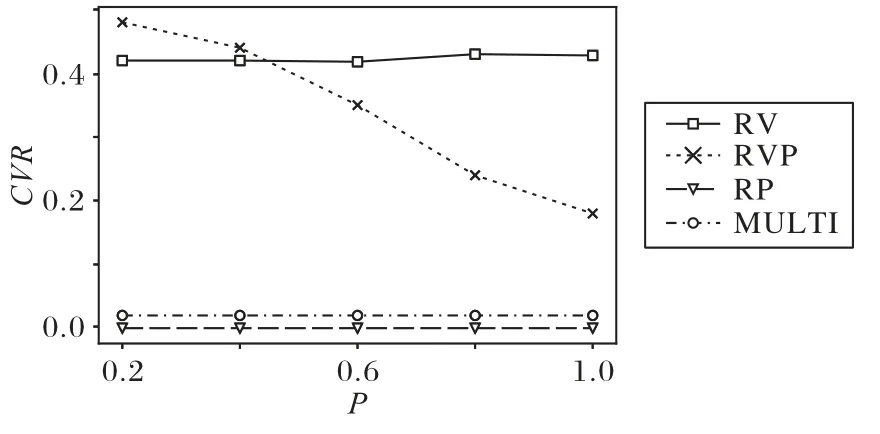
圖5 CVR與P的關系Fig.5 Relationship between CVR and P

實驗3 的R分別取3、5、7 時，資源需求量的分布如表9 所示。實驗結果如表10～11，四種算法的MIG和CVR都比較穩定，RVP的MIG與MULTI的MIG保持著4倍左右的差距。

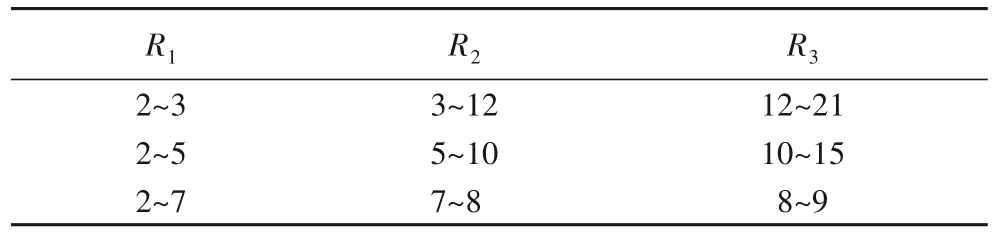
表9 P不變時資源需求量的分布Tab.9 Distribution of Resource Demand with fixed P

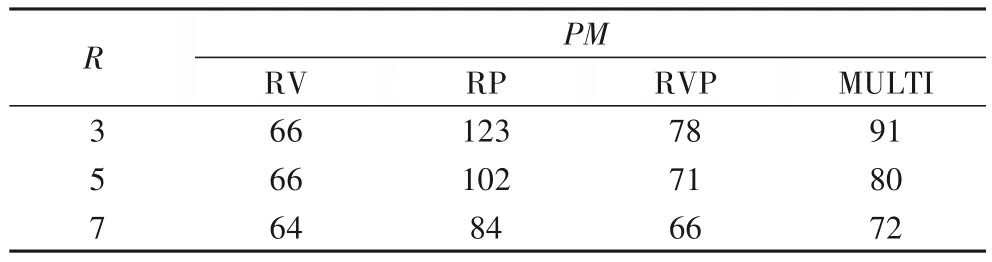
表10 PM與R的關系Tab.10 Relationship between PM and R

實驗4的結果如圖6所示，部署時間與當前已放置的容器數量呈線性關系，當已部署的容器數量過大時，部署時間也會變得非常長，表明容器遷移開銷也相應變大。

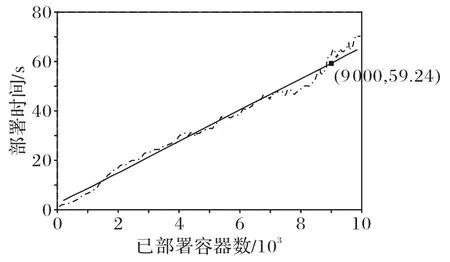
圖6 部署時延與部署容器數量的關系Fig.6 Relationship between deployment delay and number of deployed dockers

綜上所述，實驗1 體現了容器資源需求分布的期望對部署結果的影響，實驗2、3 用兩種方式調節了容器資源需求分布的方差并研究了它對部署結果的影響，進而一方面也驗證了式（10）、（11）、（12）結論的可靠性。面向多狀態負載的容器部署策略的最大優點在于能夠保持動態遷移次數和沖突率均穩定在一個較小的范圍。

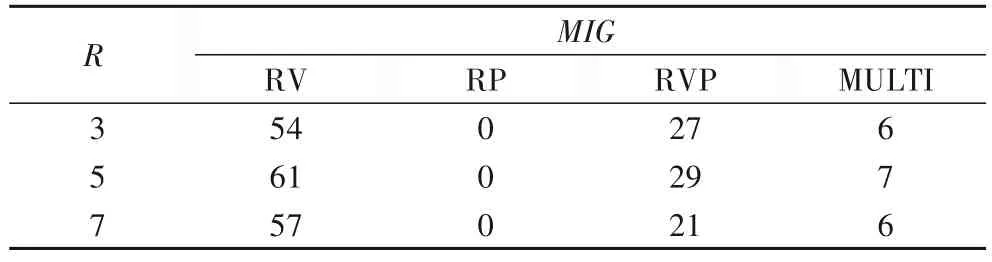
表11 MIG與R的關系Tab.11 Relationship between MIG and R

5 結語

容器技術在集群中發揮著重要作用，為用戶提供按需式的資源服務。然而，傳統被動的容器整合或是遷移無法應對動態的容器負載，給集群容器部署帶來挑戰。本文針對長效時間上容器整合與遷移的整體優化，提出了利用多狀態馬爾可夫鏈模型描述容器資源狀態，并在宿主機資源預留的基礎上提出了部署策略，還進一步優化部署的時延。實驗結果表明，本文提出的策略能夠在宿主機使用數量和動態容器遷移次數間達到較好的平衡。本文主要針對靜態場景下的動態部署問題進行了探討，但所提出的方法難以適用于在線場景，且資源需求類型的描述一定程度上影響了資源的分配策略，而資源需求的類型數量難以確定，這兩方面將是下一步研究的重點方向。