接觸網彈性吊索參數對弓網動態性能影響

關金發 ，田志軍 ，張學武

（1.中鐵第一勘測設計院集團有限公司，陜西 西安 710075；2.西南交通大學電氣工程學院，四川 成都 610031）

高速運行的受電弓要求接觸網的彈性盡可能均勻，通常用彈性不均勻度反映一跨內接觸網的彈性均勻程度.接觸網彈性與線索截面、材料、張力、跨距、結構高度、預弛度、有無彈性吊索及彈性吊索參數有關[1].接觸網彈性均勻程度是弓網穩定運行的主要條件，接觸網彈性均勻程度越小，弓網運行越穩定[2].《高速鐵路設計規范》（TB 10621—2004）[3]中提到當使用雙弓運行時，較小的彈性不均勻度是弓網動態關系可以接受的前提保障之一，宜采用彈性鏈形懸掛.TB 10621《高速鐵路設計規范條文說明》（TB 10621—2004）[4]中提出不同速度等級的推薦方案.其中 250 km/h 等級分兩種：O2-1 懸掛系統中彈性吊索張力選用2.8～3.5 kN，O2-2懸掛系統中彈性吊索張力選用3.5 kN；O3-1懸掛系統中彈性吊索張力選用3.5 kN.彈性吊索長度根據跨距和系統動態性能進行確定，一般為14～22 m[4].但調研相關標準并未給出彈性吊索參數的選取依據.

為獲取彈性吊索參數的合理范圍，可利用弓網動態仿真技術，預測不同彈性吊索參數組合下的弓網動態性能.文獻[5-6]概述了弓網動態仿真建模的主要方法，并總結了十個國際上的弓網仿真程序的仿真效果；文獻[7-9]分別研究了承力索張力、接觸線弛度、表面不平順和錨段關節對弓網動態性能的影響；文獻[10-11]分別研究了受電弓、接觸網空氣動力對弓網動態性能的影響；文獻[12-13]研究了雙弓運行下弓間距對弓網動態性能的影響；文獻[14]利用弓網動態仿真，建立單個DSA380型受電弓與德國Re330型彈性鏈形懸掛接觸網的仿真模型，研究不同接觸網參數對弓網動態性能的影響，并提出了Re330型接觸網參數的選取范圍，其中彈性吊索張力不小于 3.5 kN，長度取 16～18 m.Re330 型接觸網參數與中國高鐵接觸網參數有一定區別，且中國高鐵較多使用雙弓運行，后弓的弓網動態性能受到前弓的影響，雙弓作用下不同彈性吊索參數對弓網動態性能的影響規律尚不明確.

基于此，針對中國高鐵典型接觸網參數中的彈性吊索參數選取仍需進一步深入研究.利用經工程驗證的弓網仿真建模方法，建立不同速度等級的弓網動態仿真模型，分析雙弓作用下彈性吊索參數對弓網動態性能影響，確定弓網動態性能較優的彈性吊索參數組合，從而減小弓網振動，延長設備壽命，為接觸網系統設計提供參考依據.

1 弓網動態仿真建模及模型參數

利用文獻[15]提出的經京津城際、京滬高鐵實際測量數據驗證過的受電弓與接觸網動力學仿真建模方法，受電弓與接觸網仿真模型采用有限單元法，弓網接觸模型采用罰函數法，建立250 km/h和350 km/h兩個速度等級的受電弓與接觸網動態仿真模型.

受電弓的動力仿真模型如圖1所示，為三質量-剛度-阻尼歸算質點模型.圖中：m3、m2、m1分別為弓頭、上框架、下臂桿歸算質量；c3、c2、c1分別為弓頭、上框架、下臂桿歸算阻尼；k3、k2、k1分別為弓頭、上框架、下臂桿歸算剛度；fc為弓網接觸力；f0為靜態接觸力；y3、y2、y1分別為弓頭、上框架、下臂桿歸算坐標.250 km/h 線路的受電弓為DSA250 型；350 km/h線路的受電弓為DSA380型、SSS400+型和CX-NG型.其中DSA250型和DSA380型受電弓模型參數見表1[16].

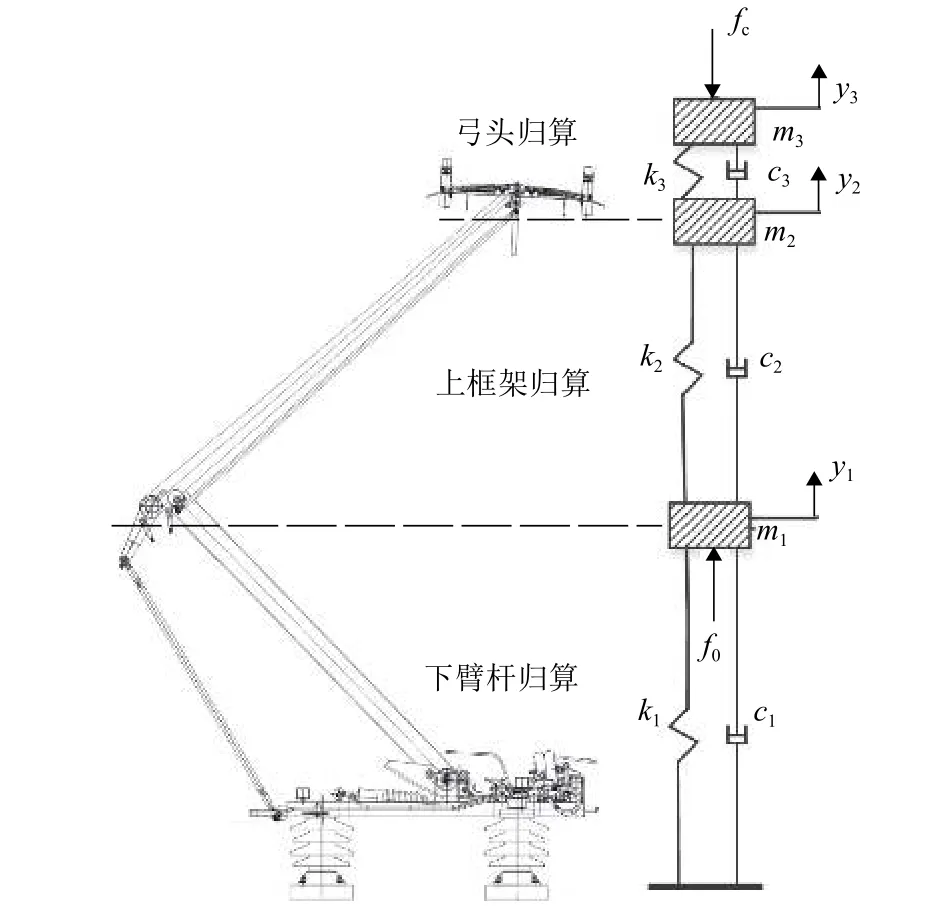
圖1 受電弓三質量塊歸算模型Fig.1 Three-mass model of pantographs

表1 受電弓模型參數Tab.1 Model parameters of pantograph

不同運行速度下空氣對受電弓產生一定的動態升力，以標準EN 50367[17]中提到的受電弓平均抬升力目標曲線為參考依據.交流受電弓速度大于200 km/h 的最大平均抬升力為(70+0.00097v2) N，（v為運行速度，km/h）.選用最大平均抬升力曲線作為計算的平均抬升力.考慮8輛編組列車重聯或16輛編組動車組，雙弓運行，弓間距取200 m.

標準TB 10621[4]中對接觸網懸掛系統主要設計參數有所規定，250 km/h線路以O2-1中接觸網為例，350 km/h線路以O3-1中京滬高鐵接觸網為例，其懸掛參數如表2所示.根據接觸網的建模方法及相關參數，建立接觸網的仿真模型，如圖2所示.

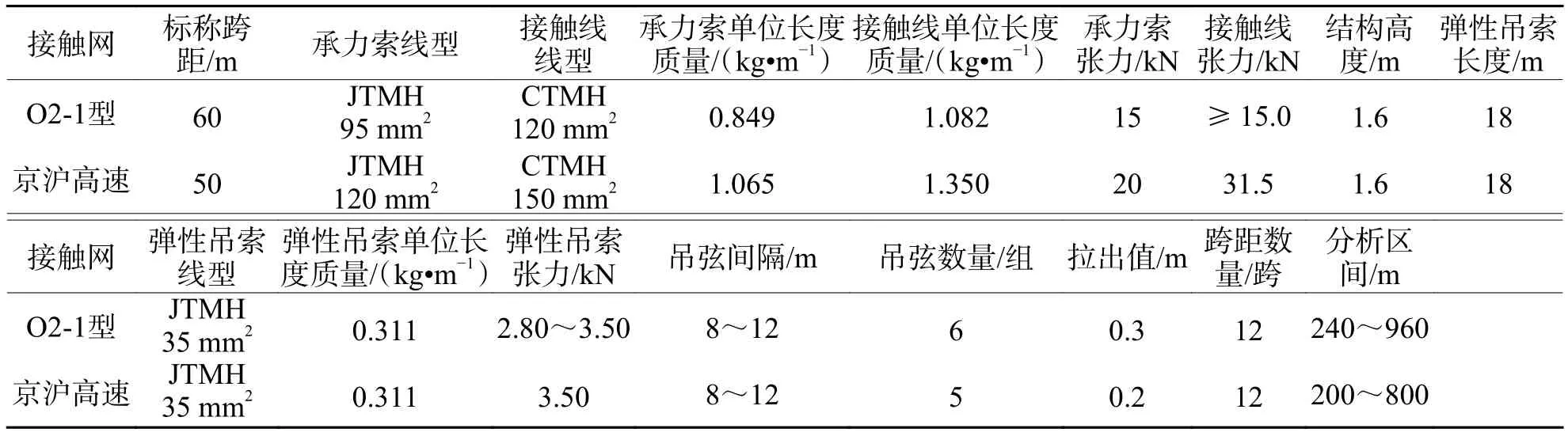
表2 接觸網設計參數Tab.2 Catenary design parameters

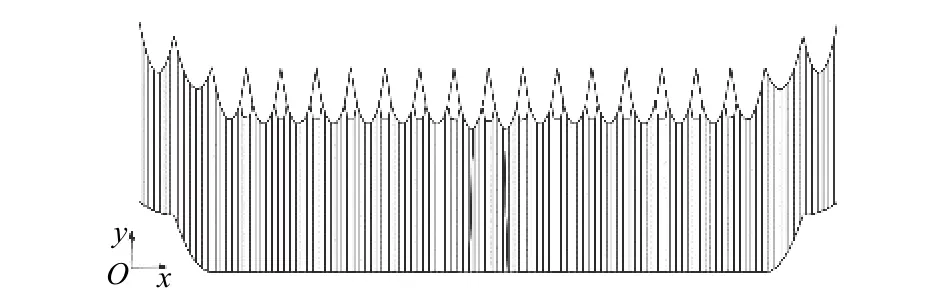
圖2 接觸網仿真模型Fig.2 Catenary simulation model

利用罰函數解決弓網接觸問題，令接觸線單元i?j與質量點m3的垂直方向滲透位移為ξ，假設質量點m3在單元i?j上方，ξ為正值，此時為接觸狀態，反之質量點m3在單元i?j下方，ξ為負值，此時為分離狀態，見圖3.

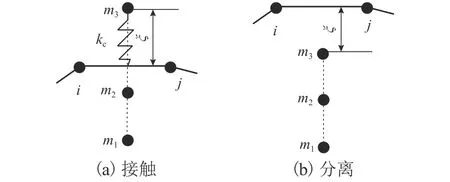
圖3 弓網接觸模型Fig.3 Pantograph-catenary contact model

當分離狀態下接觸剛度kc為0.當接觸狀態下kc為一正常數.接觸力為

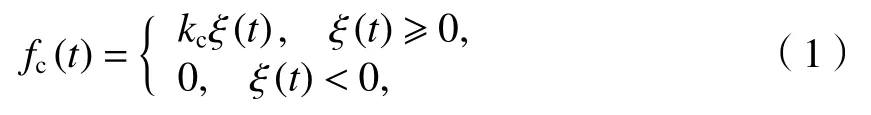
式中：t為時間；參考 EN 50367[17]，kc取 50 kN/m.

表2接觸網參數中的O2-1接觸線張力尚不確定，若采用15 kN，利用接觸網仿真建模方法，建立O2-1接觸網的仿真模型，以70 N的靜態力計算一跨內的彈性分布，如圖4所示.由圖4可計算出彈性不均勻系數為16.64%.按照 TB 10621[4]規定，接觸網彈性不均勻系數在250 km/h速度等級需小于15.00%，大于 300 km/h 速度等級需小于 10.00%.顯然接觸線張力為15 kN，彈性不均勻系數超出了標準要求，將O2-1接觸線張力提升至18 kN，則接觸網彈性所有減小，此時的接觸網彈性不均勻系數為14.99%，滿足標準要求，以該值進行進一步分析.京滬高鐵接觸網的彈性不均勻系數為8.73%，滿足標準要求.

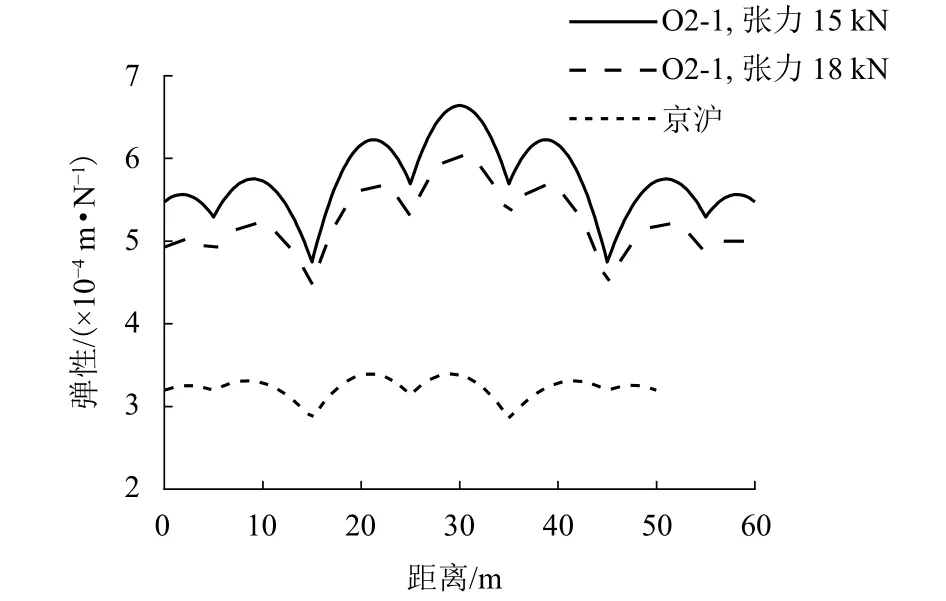
圖4 250 km/h和350 km/h 速度等級接觸懸掛彈性曲線Fig.4 Elastic curves of contact suspension at 250 km/h and 350 km/h

在材料確定后，彈性吊索有3個主要參數，分別為截面積、張力和長度.根據承力索銅絞線標準[18]：2.80 kN 適用的絞線型號為JTMH 25；3.50 kN 適用的絞線型號為JTMH 35.考慮彈性吊索張力變化范圍為2.80、3.15、3.50、3.80 kN，則絞線截面積為25 mm2和 35 mm2，長度選取 14、16、18、22 m，以下分別建立不同彈性吊索參數下的O2-1、京滬高鐵弓網仿真模型，分析彈性吊索參數對弓網動態性能的影響.

2 彈性吊索參數對弓網動態性能影響

2.1 彈性吊索截面積對弓網動態性能的影響

彈性吊索長度為18 m，當張力為2.80 kN時，對應截面積選 25 mm2和35 mm2.分別計算這兩種工況的O2-1、京滬高鐵接觸網的弓網動態性能.

DSA250型受電弓以250 km/h雙弓運行在O2-1接觸網，經弓網仿真計算得到接觸力曲線如圖5所示.前弓接觸力曲線相差不大，后弓兩種工況的接觸力曲線有一定差別，彈性吊索截面積為25 mm2的接觸力波動較35 mm2的大.

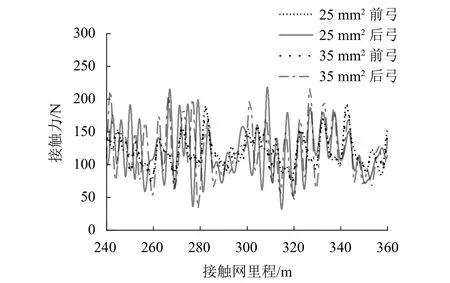
圖5 250 km/h 等級接觸網接觸力Fig.5 Catenary contact force at 250 km/h

統計250 km/h等級接觸網兩種工況分析區段內的接觸力和定位點抬升數字特征，如表3所示.表中：Fm、Fmin和Fmax分別為接觸力的平均值、最小值和最大值；σ為接觸力標準差；dup為定位點最大抬升量.由表3可知：不同彈性吊索截面積的后弓的接觸力標準差均較前弓大；后弓通過彈性吊索截面積為35 mm2的接觸力標準差較 25 mm2小，說明 O2-1接觸網彈性吊索截面積為35 mm2的弓網接觸質量明顯較優；O2-1接觸網彈性吊索截面積變化對定位點抬升影響不大.綜合以上分析，得到O2-1接觸網彈性吊索截面積宜選用35 mm2.

表3 250 km/h等級接觸網接觸力統計值Tab.3 Catenary contact force statistics at 250 km/h level

DSA380型受電弓以350 km/h雙弓運行在京滬高鐵接觸網，經弓網仿真計算，得到接觸力曲線如圖6所示.雙弓接觸力曲線不重合，但波動幅值接近.

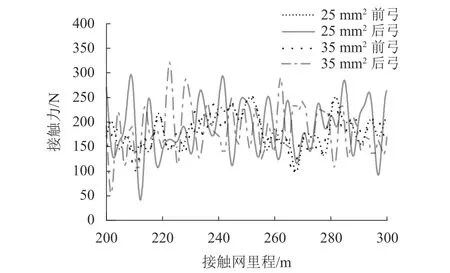
圖6 350 km/h 等級接觸網接觸力Fig.6 Catenary contact force at 350 km/h

350 km/h等級接觸網的接觸力數字特征如表4所示.發現不同彈性吊索截面積的后弓的接觸力標準差均較前弓大，后弓通過彈性吊索截面積為35 mm2的接觸力標準差較25 mm2小，說明京滬高鐵接觸網彈性吊索截面積為35 mm2的弓網接觸質量較優.彈性吊索截面積為25、35 mm2的定位點最大抬升量分別為102.3、102.2 mm，說明京滬高鐵接觸網彈性吊索截面變化對定位點抬升影響不大.綜合以上分析，得到京滬高鐵接觸網彈性吊索截面積宜選用 35 mm2.

表4 350 km/h等級接觸網接觸力統計值Tab.4 Catenary contact force statistics at 350 km/h

2.2 彈性吊索張力對弓網動態性能的影響

彈性吊索長度為18 m，當截面積選35 mm2時，對應張力可為2.80、3.15、3.50、3.80 kN.分別計算O2-1、京滬高鐵接觸網在不同張力下的接觸力統計特征值和定位點最大抬升量，如圖7和圖8所示.

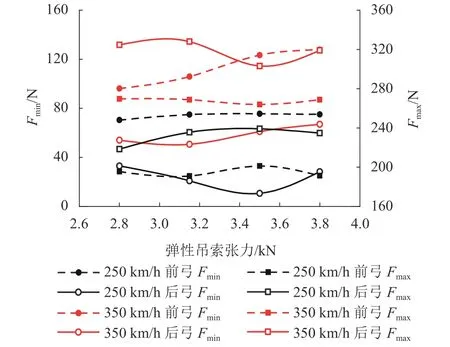
圖7 不同彈性吊索張力的接觸力最值Fig.7 Maximum and minimum contact forces with different stitch wire tensions

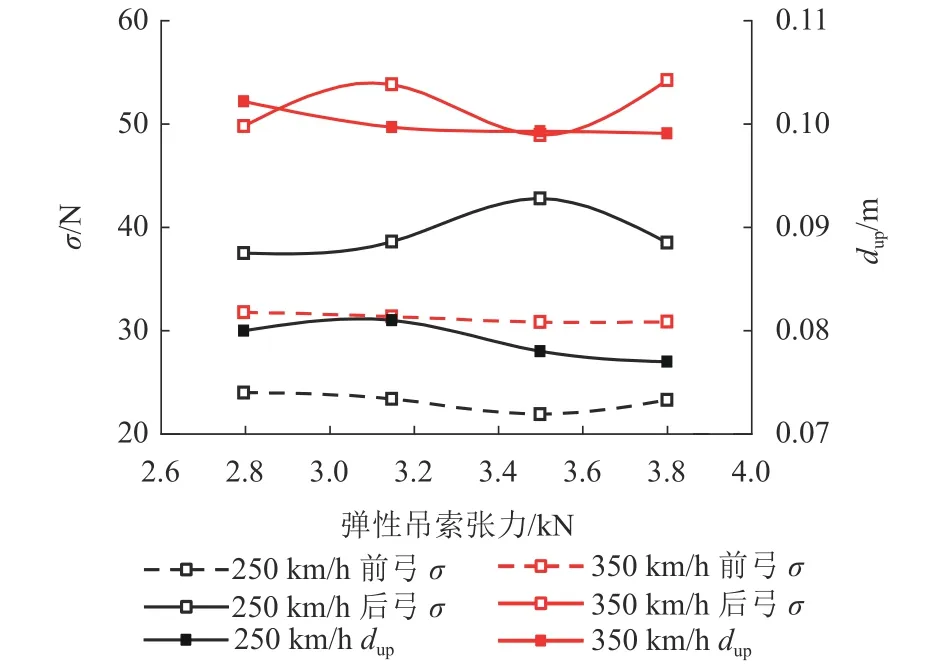
圖8 不同彈性吊索張力的接觸力標準差和定位點最大抬升Fig.8 Standard deviation of contact force and maximum uplift at supporting points with different stitch wire tensions

對于250 km/h等級接觸網，隨著張力的增加，前弓接觸力最小值和最大值的變化并不明顯，但后弓則有較明顯的變化，后弓接觸力最大值逐漸變大，最小值先變小再變大，O2-1接觸網彈性吊索張力為2.80 kN時，后弓接觸力最值之差最小；且隨著張力的增加，定位點最大抬升緩慢變小，前弓接觸力標準差變化不大，而后弓接觸力標準差的變化較明顯，O2-1接觸網彈性吊索張力為2.80 kN時，后弓接觸力標準差最小.綜合以上分析，得到O2-1接觸網彈性吊索張力標稱值宜選用2.80 kN.

對于350 km/h等級接觸網，隨著張力的增加，前弓接觸力最值之差變大，而后弓接觸力最大值先逐漸變小再變大，最小值逐漸變大，京滬高鐵接觸網彈性吊索張力為3.50 kN時，后弓接觸力最值之差最小.且隨著張力的增加，定位點最大抬升緩慢變小，前弓接觸力標準差變化不大，而后弓接觸力標準差的變化較明顯，京滬高鐵接觸網彈性吊索張力為3.50 kN時，后弓接觸力標準差最小.綜合以上分析，得到京滬高鐵接觸網彈性吊索張力標稱值宜選用3.50 kN.

考慮現場安裝彈性吊索張力存在一定的施工公差，O2-1接觸網彈性吊索張力在2.80 kN附近100 N的特征值與2.80 kN的特征值接近，京滬高鐵接觸網彈性吊索張力在3.50 kN附近100 N的特征值與3.50 kN的特征值接近，因此，O2-1接觸網和京滬高鐵接觸網彈性吊索張力宜選用的范圍分別為(2.80 ±0.10) kN和(3.50 ± 0.10) kN.

2.3 彈性吊索長度對弓網動態性能的影響

當截面積選35 mm2和張力選2.80 kN時，彈性吊索長度分別取 14、16、18、22 m，分別計算 O2-1、京滬高鐵接觸網在不同彈性吊索長度下的接觸力統計特征值和定位點最大抬升量，如圖9和圖10所示.

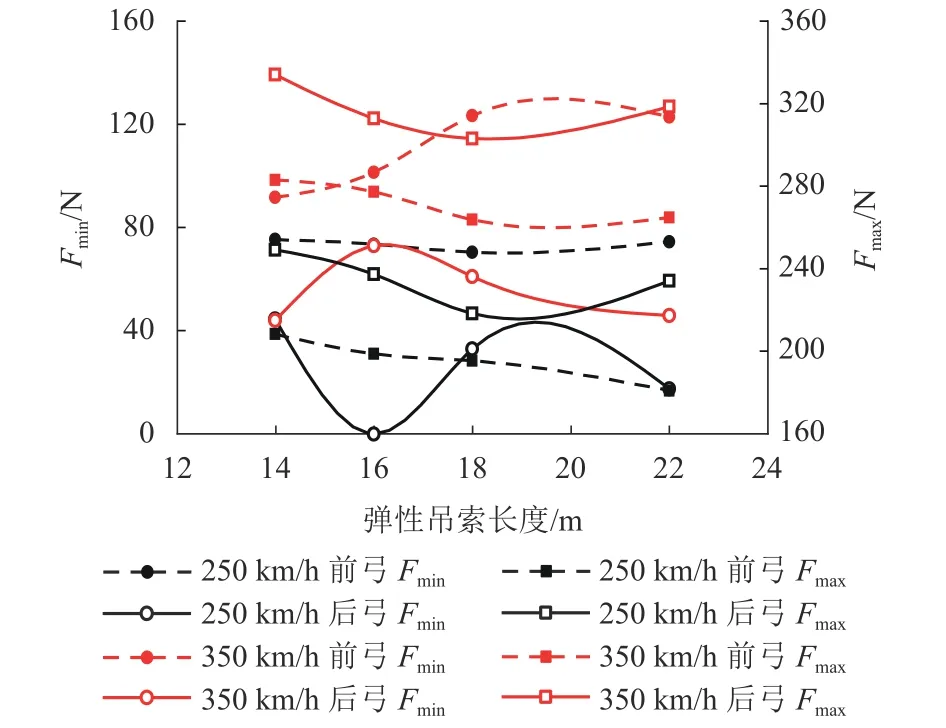
圖9 不同彈性吊索長度的接觸力最值Fig.9 Maximum and minimum contact forces with different stitch wire lengths

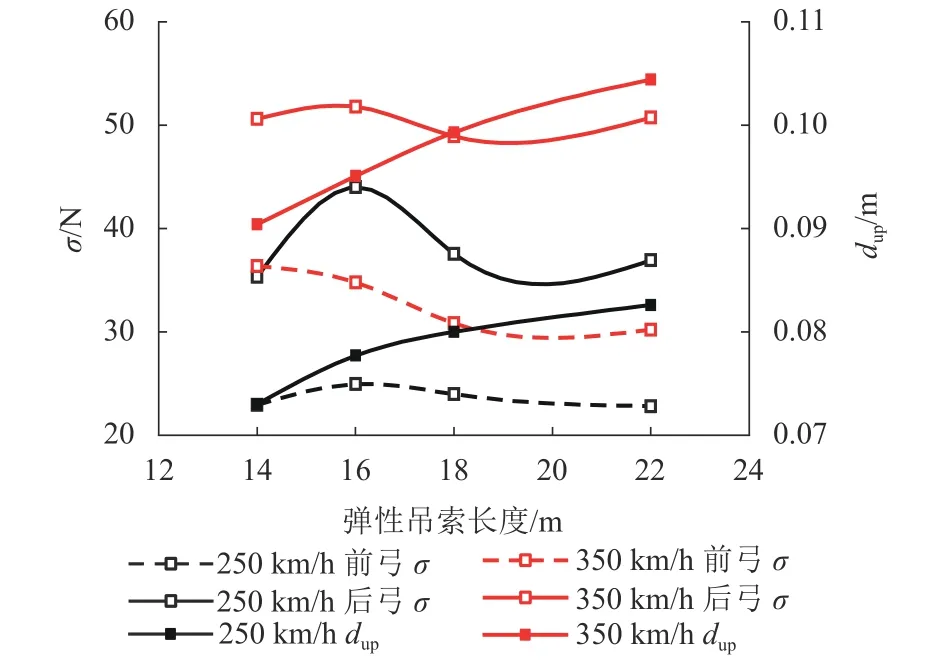
圖10 不同彈性吊索長度的接觸力標準差和定位點最大抬升Fig.10 Standard deviation of contact force and maximum uplift at supporting points with different stitch wire lengths

對于250 km/h等級接觸網，隨著長度的增加，O2-1接觸網的前弓接觸力最值之差緩慢變大，后弓接觸力最值之差在長度18 m時最小，值得注意當長度為16 m時，后弓接觸力最小值為0，應避免長度選取16 m；且隨著長度的增加，定位點最大抬升量逐漸增加，前弓接觸力標準差變化不大，后弓接觸力標準差先變大再變小，當長度為14 m時，后弓接觸力標準差最小，定位點最大抬升量最小，當長度為18 m時，后弓接觸力標準差與長度為14 m接近，但定位點最大抬升量相差8 mm.綜合分析以上分析，得到O2-1接觸網彈性吊索長度宜選用14 m或18 m.

對于350 km/h等級接觸網，隨著長度的增加，京滬高鐵接觸網的前弓接觸力最值之差逐漸變大，后弓接觸力最值之差在長度16 m和18 m較小；且隨著長度的增加，定位點最大抬升量逐漸增加，雙弓接觸力標準差先減小在緩慢變大，當長度為18 m時，雙弓接觸力標準差最小，長度為18 m的定位點最大抬升量與長度為14 m相差10 mm.綜合以上分析，得到京滬高鐵接觸網彈性吊索長度宜選用18 m.

250 km/h和350 km/h 下彈性吊索長度 22 m 的定位點最大抬升分別是18 m的111%和117%.

3 結 論

1）比較不同彈性吊索參數的弓網動態性能指標，得到適應250 km/h速度等級的O2-1型接觸網彈性吊索宜選用線型為JTMH 35 mm2、張力標稱值為2.80 kN、張力范圍為(2.80 ± 0.10) kN 和長度為14 m或18 m；適應350 km/h速度等級的京滬高鐵接觸網彈性吊索宜選用線型為JTMH 35 mm2、張力標稱值為3.50 kN、張力范圍為(3.50 ± 0.10) kN 和長度為18 m.

2）不同工況下雙弓通過 250 km/h和350 km/h兩種接觸網懸掛系統，后弓的接觸力波動均比前弓大.彈性吊索參數變化對前弓的接觸力影響較小，對后弓的接觸力影響顯著.

3）250 km/h和350 km/h 下彈性吊索張力的變化對定位點最大抬升影響較小.250 km/h和350 km/h下彈性吊索長度22 m的定位點最大抬升是長度18 m的111%和117%，彈性吊索長度的變化對定位點最大抬升影響顯著.

致謝：中鐵第一勘察設計院院科18-30科研項目的資助.