基于模型預測控制的飛翼無人機抗側風著陸規劃技術

邵朋院 董彥非 屈高敏

（西安航空學院飛行器學院 陜西省西安市 710000）

飛機著陸階段是最容易出現飛行事故的階段之一，而惡劣天氣是導致著陸時發生飛行事故的最主要原因[1]，其中側風是對飛機著陸影響最大的因素。在側風作用下，飛機會產生側向力和力矩，其中側向力會使飛機運動軌跡偏離預訂航跡，側向力矩會使飛機帶有一定的滾轉角和偏航角。同時，在側風作用下，飛機會產生較大側滑角，側滑角過大會嚴重影響飛機的內環控制性能和穩定性。特別是對于飛翼無人機來說，側向只能使用阻力方向舵進行控制，控制能力較差[2]，所以在著陸階段側風對其內環控制影響更大。

目前，在側風中著陸的橫側向控制策略主要有側航法和側滑法兩種[3]。側航法通過將機頭方向朝向側風方向，而消除側滑角，但是由于機頭方向和跑道方向不一致，所以在接地后飛機滑跑方向與跑道中心線方向也不一致，在側偏角過大時有沖出跑道的危險；側滑法機頭方向與跑道及地速方向一致，由于有側風存在，會存在一定側滑角，并且為了平衡側滑角造成的側力，需要飛機帶一定的滾轉角，而對于展弦比較大的飛翼無人機，在大滾轉角下有翼尖觸地的風險，也會影響飛行安全。關于側航法和側滑法著陸的原理和存在問題的詳細分析，見本文第1 小節。

綜上所述，飛翼無人機單純用側航法和側滑法著陸都存在一定問題，本文結合側航法和側滑法的優點，提出一種基于模型預測控制（ModelPredictiveControl, MPC）[4]方法進行運動規劃的抗側風控制策略。該策略從著陸拉平段開始，在側向通過MPC 規劃，規劃出一條可行的動作軌跡，使得著陸瞬間飛機的狀態滿足指定值或者指定范圍約束。使用該策略可以提高飛機在復雜天氣情況下的著陸安全性。

1 著陸規劃策略

1.1 橫側向運動模型

為了便于橫側向運動進行分析與設計，先給出飛翼無人機的橫側向運動模型。由于本文研究重點為著陸策略，為簡化問題，所以只給出外環運動模型。

如圖1所示，為簡化期間，設跑道方向為正北，則飛機的偏航角即為機頭和跑道之間的夾角（后文中簡稱為交叉角）。則空速為：

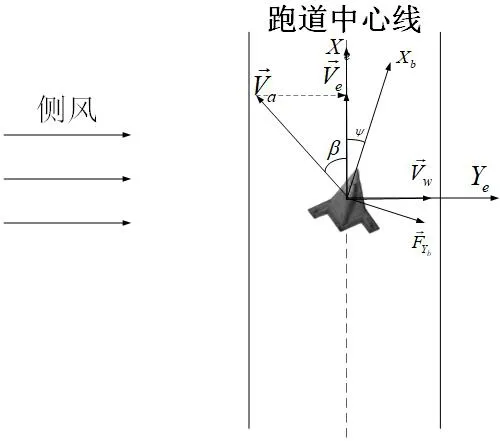
圖1：風場下受力分析圖（側向）

選取系統狀態變量為：

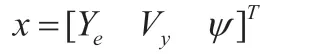
輸入為：

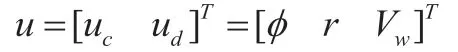
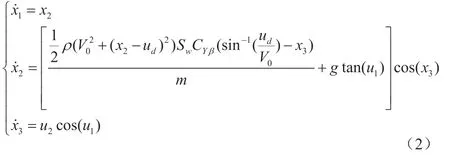
下面根據式（2）可以對側滑法及側航法的著陸策略進行分析，并提出本文的著陸策略。

1.2 已有方案分析

1.2.1 側航法

側航法示意圖如圖2所示。

圖2：側航法示意圖

如圖2所示，側航法著陸時飛機機頭會往側風向偏移，形成一定的交叉角。側航法其實是飛機側風著陸時在航向靜穩定性下的正常響應，在航向靜穩定性的作用下，飛機的側滑角為0，所以側向力也為0，從式（5）可知，在滾轉角也為0 的情況下，則飛機可以維持側向位置的平衡。

所以，在側航法著陸策略作用下，優點是飛機的滾轉角為0，側滑角為0，所受側向力即（飛機的側向載荷）為0；缺點是交叉角不為0，即機頭方向和跑道方向不一致，若一直以側航法著陸，則在接地時，飛機的滑跑方向與跑道方向差別較大，有沖出跑道的危險。

1.2.2 側滑法

側滑法的原理如圖3所示。在側滑法策略作用下，飛機機頭方向和跑道方向一致，避免了接地后滑出跑道的危險。結合式（2），要使飛機的側向位置達到平衡，則需要滿足。

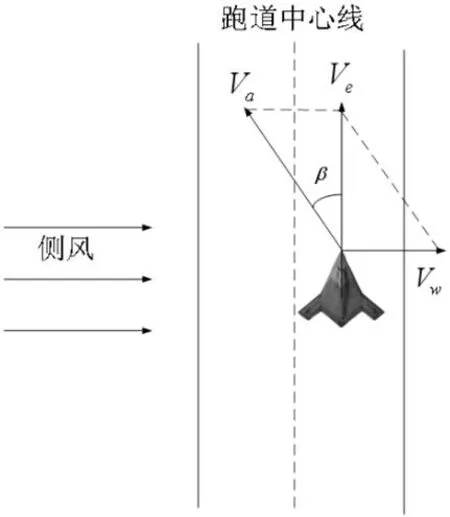
圖3：側滑法示意圖

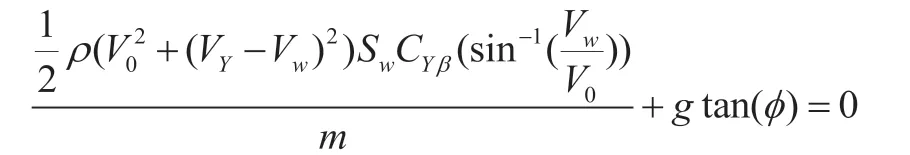
當飛機的著陸速度和風速都確定的情況下，側滑角及側力也已確定，即側向力為：

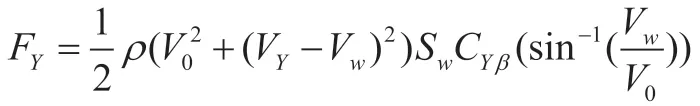
要側向運動平衡，則有：

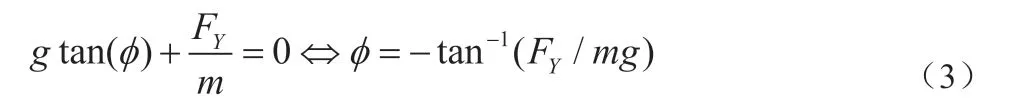
所以需要滿足式（3）才能使得側向運動平衡，即飛機一直沿著跑道中心線下滑著陸。但是在穩態時會帶一定的滾轉角。同時，側滑角為固定值，由于側滑法與側航法穩態速度一致，所以側滑角與式（2）的中對應側滑角值相同。

所以，側滑法雖然能滿足飛機機頭方向與跑道方向一致（即交叉角為0），但是在穩態時必須帶有一定的滾轉角和側滑角，對于無尾飛翼飛機來說，側滑角對著陸影響較小，但是滾轉角過大也對著陸安全不利，對于大展弦比飛機有翼尖著陸的危險。而且，在著陸末端使用側滑法，則飛機喪失了側向糾偏能力，所以在著陸末端也無法保證糾偏。以上分析表明，使用側滑法也不能滿足飛翼無人機側風著陸的要求。

1.3 本文提出策略

從上述分析可知：側航法的主要問題是機頭方向和跑道方向不一致，而優點是沒有側滑角，從而沒有側力，無需滾轉角即可平衡；側滑法的主要問題是需要滾轉角來使用升力分量來平衡側力，而且喪失了側向糾偏能力，而優點是機頭和跑道方向一致，及交叉角為0。

在著陸末端，如果滿足側向偏離，側向速度，交叉角及滾轉角均為0，則能實現比較理想的著陸。即：

若在接地時，滾轉角和交叉角均為0，由式（2）可知：

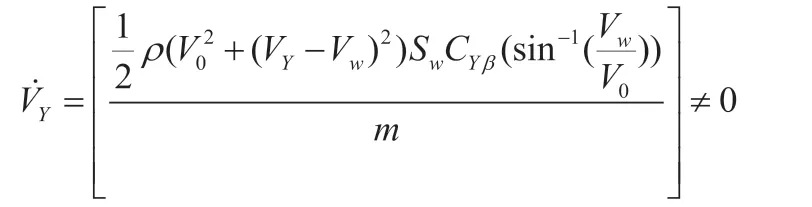
所以，式（4）的條件無法在穩態實現。

本文提出一種能夠在接地時實現式（4）終端條件的著陸策略。

該策略無需在接地時達到穩態，可以保證在接地時達到式（4）的狀態。由于側航法是飛機在側風下著陸的自然響應，所以以側航法達到穩態時的狀態為初始狀態。

設飛機的初始狀態為：

該策略即讓飛機從初始狀態（5）在接地時轉化到終止狀態（4）。如圖4所示。

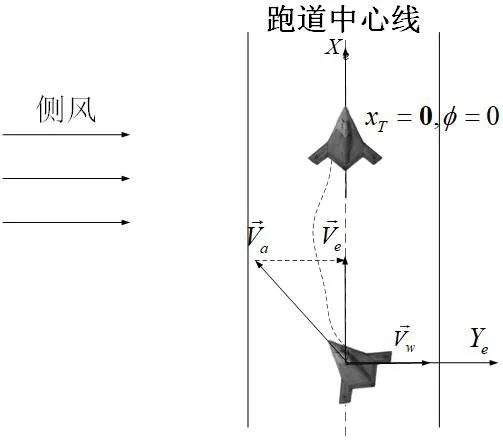
圖4：本文提出策略

假設縱向運動和橫側向解耦，則從開始高度到接地的時間確定，假設時間為，考慮到在著陸過程中盡量避免較大機動，而且側滑角過大會增加控制難度，所以以整個控制過程中控制代價和控制過程中側滑角加權代價最小為目標，記式（2）為：

其中，J 為代價函數，表達式如下：

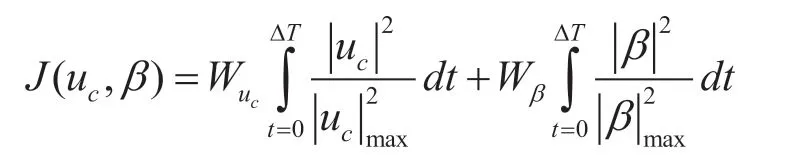
式（7）可以歸結為一個動態系統在輸入約束下從初始狀態在規定時間內運動到給定終端狀態，且使代價函數最小的動態系統軌跡優化問題，該類問題在數學上屬于最優控制問題，可以使用模型預測控制的方法進行求解。

2 問題求解

可以看出，式（6）為一個非線性系統，所以問題（7）為一個非線性模型預測控制（Nonlinear Model Predictive Control, NMPC）問題，該問題可用ACADO 工具箱[5]求解，ACADO 可以調用多種求解器使用SQP 方法[6]求解NMPC 問題，并且ACADO 工具箱提供了Matlab 接口，同時可以生成C++代碼來高效的求解最優控制問題（Optimal Control Problem, OCP）。關于ACADO 的詳細用法可以參考文獻[7]。

3 在飛翼無人機中的應用

假設著陸階段縱向與橫側向解耦，本文所研究的側向抗風運動規劃主要作用于飄落階段，飛翼無人機著陸段縱向控制律設計可以參考文獻[8]。

在飄落階段開始時，飛機的縱向運動已經達到穩態，在本例中為下沉率。在進入飄落段時，設飛行高度為H，空速為V0，則飄落時間為：。

從下滑段開始，飛機橫側向執行側向糾偏控制律，則飛機的自然響應與前文中側航法描述一致。則進入飄落段時的初始狀態已經達到如下穩態：

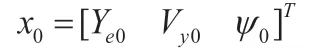
著陸末端飛機響應如圖5。

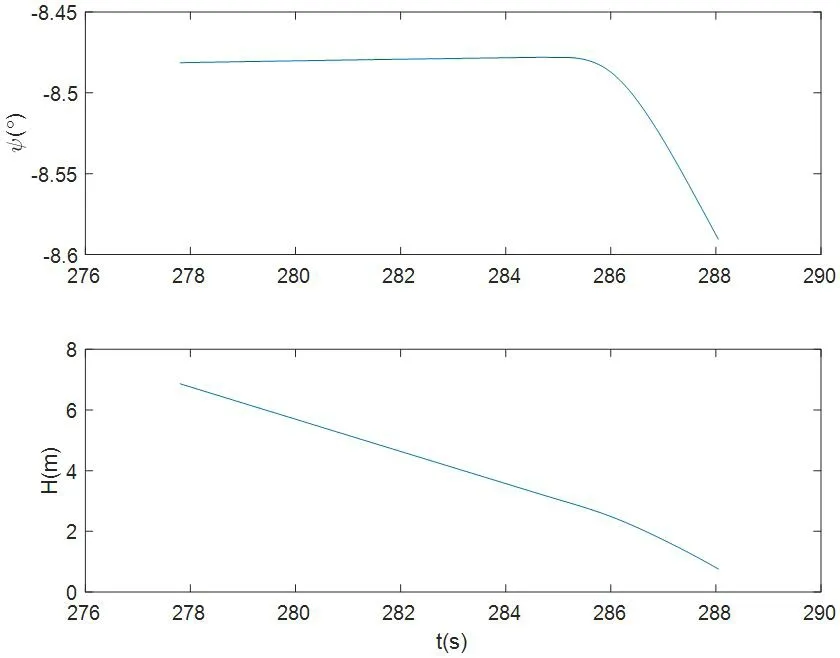
圖5：著陸末端偏航角和高度響應

從圖5可以看出，在著陸末端飛機偏航角基本穩定在8.46°左右，特別是在著陸前10 秒時基本達到穩態，在接地前的小幅波動是因為受地效影響。

以圖5 中著陸前10 秒（t=277.8s）的狀態為初始狀態，根據飛機性能約束，將滾轉角指令約束到±30deg，偏航角速率指令約束到±30deg/s。分別使用側滑法和本文提出的規劃策略。得到相關響應如圖6‐圖10所示。

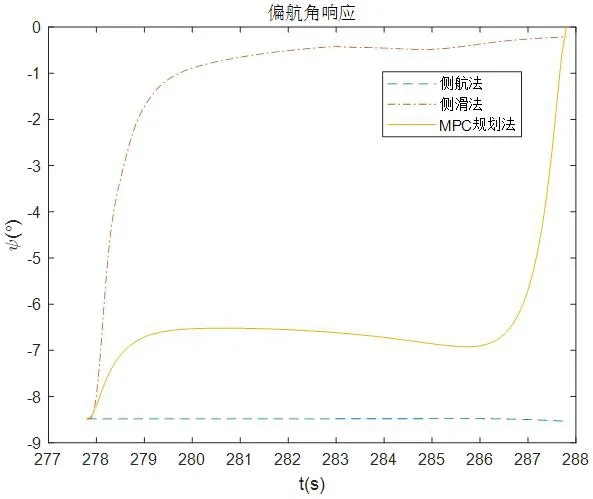
圖6：側風著陸偏航角響應

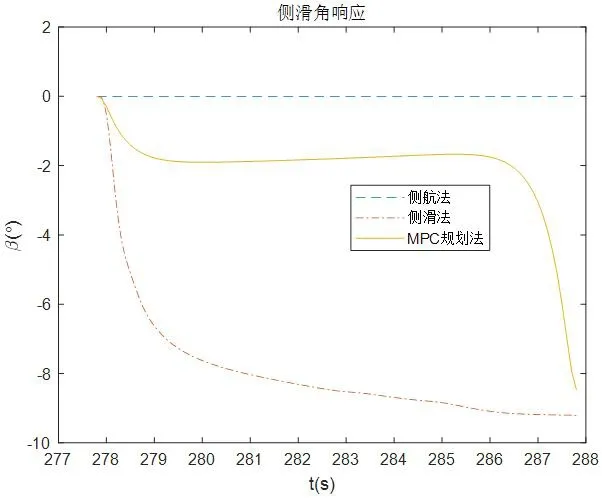
圖7：側風著陸側滑角響應

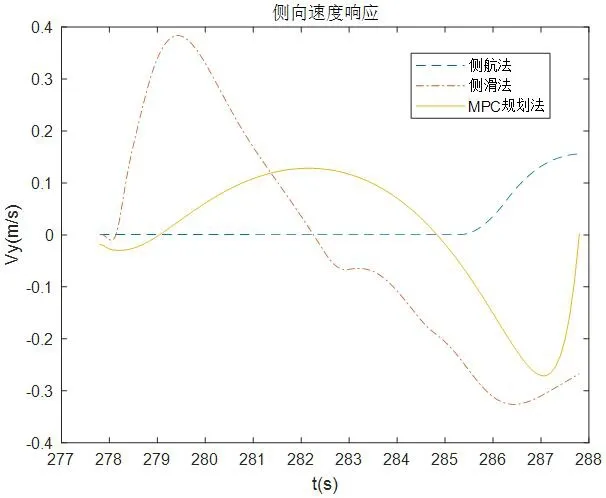
圖8：側風著陸側向速度響應

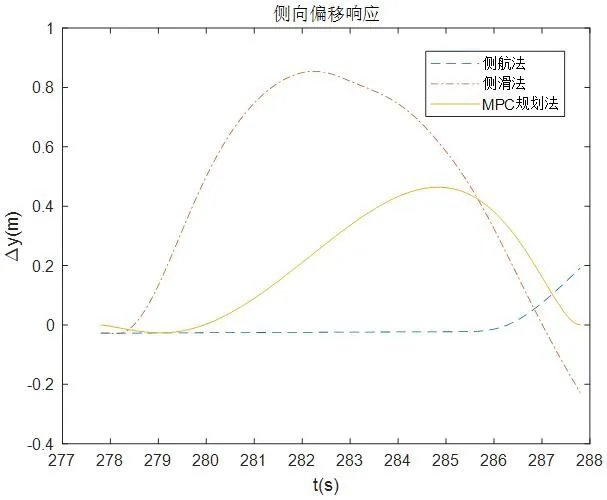
圖9：側風著陸側向偏移響應

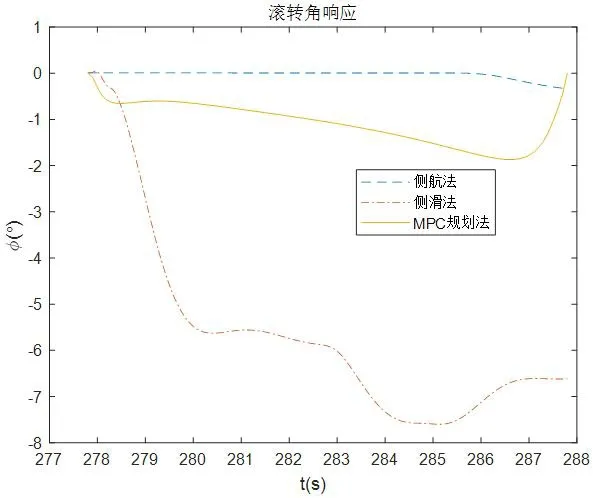
圖10：側風著陸滾轉角響應

從圖6到圖10可以看出，側航法著陸末端有個較大的交叉角（偏航角），而側滑角、滾轉角、側向偏移和側向速度接近0；側滑法著陸末端交叉角、側向偏移和側向速度接近0，而側滑角和滾轉角較大；本文提出的基于運動規劃的方法可以滿足著陸末端的交叉角、側向速度、側向偏移和滾轉角均為0，有一定的側滑角。仿真結果與第1 節理論分析一致，而飛翼無人機對于側滑角有一定的容忍能力，所以上述三種策略只有本文提出的基于運動規劃的方法可以滿足飛翼無人機側風著陸需要。

4 結束語

本文對飛翼無人機側風著陸的運動規劃策略進行了研究，提出了基于模型預測控制的著陸運動規劃方法，并通過理論分析和仿真實驗對本文提出策略和側滑法以及側航法等傳統方法進行了對比，理論分析和仿真結果均證明，在三種方法中只有本文提出的基于運動規劃的方法能夠滿足飛翼無人機側風著陸需求。

由于模型預測控制方法需要在線求解最優化問題，所以對算法的實時性要求較高，本文在仿真環境下可以滿足實時性要求，而在實際的嵌入式計算機下，設計結果能否滿足實時性要求，可能是需要下一步深入研究的一個問題。