基于SBFEM和機器學習的薄板結構缺陷反演

趙林鑫，江守燕，杜成斌

(河海大學工程力學系，南京 211100)

缺陷損傷檢測識別技術長期以來一直是結構健康監測領域的研究熱點。目前，基于振動的損傷檢測方法在土木工程、航空航天等領域得到了廣泛的應用。其檢測的基本原理是：結構振動特性是其物理參數的函數，結構損傷意味著結構物理參數的改變，而物理參數的改變必然引起結構振動特性的改變[1]。對動力測試信號進行分析和處理，可獲得結構物理參數的改變情況，達到損傷識別的目的。

目前基于振動響應的板類結構損傷檢測識別技術有很多[2?4]，其中Lamb波檢測技術由于具有傳播衰減小、傳播距離長、檢測效率高等優點，常被應用在板類結構的損傷檢測中，如基于相位延遲疊加法[5]、結合橢圓定位和數據融合的方法[6]以及小波分析法[7]等。鄭陽等[8]采集缺陷周圍的散射信號并繪制散射系數周向分布圖，根據圖形特征進行通孔和通透裂紋兩種缺陷的種類識別；劉增華等[9]對鋁板中Lamb波信號進行連續小波變換，從時頻圖中識別出缺陷信號的頻率成分，進一步實現缺陷的定位；嚴宏等[10]提取結構損傷前后的信號能量特征差異系數作為損傷指標，結合概率統計方法和成像算法，給出了損傷存在概率圖像；Moustafa等[11]基于Lamb波分形特性進行損傷檢測，并結合層析成像算法識別板狀結構中的損傷。以上研究均根據振動響應信號的變化特性，解決了板類結構中損傷種類識別以及損傷定位的問題，但未進一步實現缺陷的幾何尺寸定量反演，且一些方法存在噪聲免疫力弱的問題。實際應用中，若無法對損傷進行量化，進一步預測損傷結構的剩余壽命或剩余強度是非常困難的。因此對結構中存在的缺陷進行精確定位和定量反演對結構損傷檢測具有重要意義。

計算力學方法與智能算法的結合已廣泛應用于缺陷定量反演問題中并取得了不錯的效果[12?19]。比如，Liu等[12]和Wu等[13]利用樣條無單元法計算得到的諧波響應作為輸入參數，并結合遺傳算法計算了板類結構中缺陷的位置和大小；江守燕等[14]基于頻率和模態保證準則，結合擴展有限元法和人工蜂群算法，建立了結構內部多缺陷反演模型；張偉等[15]通過有限元法獲取數據樣本，用波形逼近技術提取了檢測信號特征，并引入支持向量機，實現了較高精度的缺陷尺寸遠場渦流檢測定量反演；Ma等[16]和Du等[17]基于動力擴展有限元法和人工智能算法均實現了結構內部多缺陷的數量、大小和位置的精確反演。然而，上述研究雖然一定程度上解決了缺陷定量反演的問題，但也存在目標函數最小化迭代過程中耗時計算的問題。

論文基于單隱含層神經網絡建立動力響應與缺陷尺寸之間的非線性映射關系，結合機器學習和比例邊界有限元法(Scaled Boundary Finite Element Method，SBFEM)的優點，建立適用于薄板結構裂紋狀缺陷識別的反演模型，并研究該反演模型在測量噪聲影響下的魯棒性問題。

1 波動問題的比例邊界有限元法

1.1 比例邊界有限元法基本公式

在SBFEM中，僅需要對區域邊界進行離散，因而可以使得計算維度降低一維[20?21]。如圖1所示，定義局部坐標系 ξOη ，其中 ξ為徑向坐標，η為環向坐標。在 ξ=0處設置一個比例中心，比例中心需要滿足對子域中任何一點的可見性。在環向邊界上， ξ=1。對于包含裂紋的子域，裂紋尖端即為比例中心，通過在與裂紋面相鄰的兩個邊界單元之間留下一個小的間隙來模擬裂紋，裂紋面無需離散。在以比例中心為坐標原點O的笛卡爾坐標系xOy中，子域內的任意一點可以用 ξ 和 η表示為：

圖1 SBFEM子域示意圖Fig. 1 Subdomain in the SBFEM

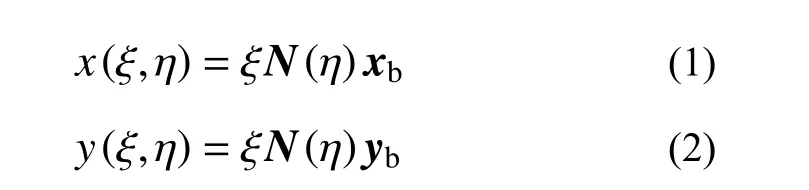
式中：N(η) 為邊界單元形函數矩陣；xb、yb為邊界上單元結點的笛卡爾坐標向量。

局部坐標系 ξOη下的位移場可表示為：

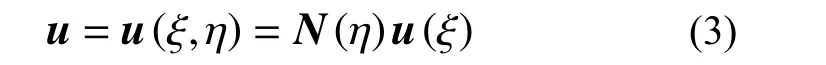
由式(3)可知，在推導任意點的位移時，SBFEM僅在環向 η方向上采用插值函數，在徑向 ξ方向上是解析的。

在二維情況下，SBFEM動力平衡方程為[22?23]：

引入動力剛度矩陣S(ω,ξ)，式(4a)可以演變為含變量ξ 、ω的常微分方程，于是，得到采用動力剛度矩陣描述的平衡方程：

在邊界 ξ=1上，動力剛度矩陣可以表示為靜力剛度矩陣K、質量矩陣M以及高階項的組合[24]，參見文獻[25]引入輔助變量改進連分式，能夠在一定程度上提高計算結果的穩定性。時域分析的離散方程可表示為：

其中：

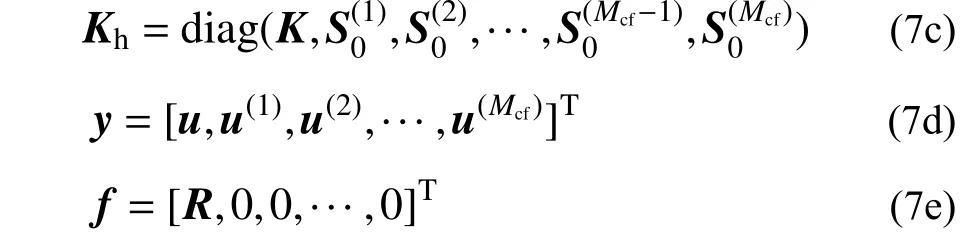
采用Newmark隱式時間積分算法可求解離散方程式(7a)。在常規有限元法中，當裂紋的長度或開裂角發生改變時，需要對網格進行重劃分，而在SBFEM中，可以通過改變裂紋所在子域的比例中心的位置對裂紋進行改變，一定程度上減少了需要進行重劃分的網格數量，提升了計算效率，在對裂紋結構的模擬計算中具有一定的優勢[26]。

1.2 波動問題的求解

數值模擬中，需要已知傳播Lamb模態的波數，并利用群速度來獲得建模的時間范圍。用SBFEM可以非常有效地計算薄板結構的波動問題。波動問題可轉化為板中波數k的標準特征值問題[27 ? 28]：

式中：u(ξ) 和q(ξ)分別為結點位移和結點力在頻域中的幅值；i為虛數單位。

對給定頻率ω求解式(8a)，得到波導模態的波數k。特征向量 Ψ (ξ)定義了模態振型，即結點處特定模態的位移和力的振幅。計算了與頻率ω相關的模態波數k后，群速度cg(ω)可通過下式得到：

2 基于機器學習算法的缺陷反演模型

機器學習是通過數據進行建模的技術，數據指的是文檔、圖像、聲音等各類信息，模型是機器學習的最終輸出結果，機器學習在建立模型過程中所使用的數據叫做“訓練數據”，圖2給出了建立機器學習模型的流程。機器學習建立模型的核心思想是在不容易建立公式和規則的情況下，使用訓練的數據“通過合適的算法構建出一個模型”[29?30]，因此，獲取足夠的反映問題特性的訓練數據對于機器學習算法至關重要。

圖2 建立機器學習模型流程Fig. 2 The process of modeling machine learning

2.1 缺陷反演思路

缺陷反演需要在結構上安裝傳感器，采集結構的動力特性(頻率、振型)和動力響應(動位移、速度、加速度)。當結構發生損傷時，結構的質量、阻尼、剛度改變，量測結構的動力響應信號也隨之改變。基于這些結構振動特性的改變，便可以運用算法對結構內部的缺陷損傷進行識別。作為板狀結構中傳播的超聲導波，Lamb波在遇到板中的缺陷時，會發生散射、反射和透射現象，此時，接收到的信號幅值、頻率成分以及模態會發生變化，信號中包含了結構的缺陷信息，通過對信號進行采集分析并提取出其中所包含的缺陷信息，就可以對缺陷的存在、大小、類型以及位置等進行判別。相較于靜響應(位移、應變)，結構的動響應信息(加速度、速度、動位移等)更易通過傳感器采集得到。

圖3給出了在具有不同缺陷深度的2 mm厚薄板上施加均勻分布的對稱脈沖荷載(見3.1節式(13))激發Lamb波時某固定觀測點處的時域位移響應，當缺陷的深度分別為0.6 mm、1.2 mm、1.8 mm時，相應的時域信號如圖中所示，初始階段由于Lamb波信號尚未傳播至缺陷處，故三種信號波形重合，但當Lamb波到達缺陷時，觀測點上的波形發生變化，這種波形變化包含著缺陷信息：當缺陷深度較大時，增加的波形的y方向位移也較大。如果加以改變缺陷的個數、位置，則時域信號的波形變化更為豐富。總體而言，固定觀測點觀測到的波形隨著板中裂紋數目、裂紋長度、裂紋開裂角的改變發生變化，當入射波模態不同時，相應的波形變化也會不同[26]。由于波形變化的影響因素較多，僅通過分析固定觀測點處的波形信號變化來獲得裂紋信息難度較大。

圖3 不同裂縫深度下時域位移響應Fig. 3 Displacement responses in the time domain under different crack depths

結構的動力響應與缺陷信息間是不容易建立某種公式來描述的，基于前述機器學習算法的啟發，通過大量的訓練樣本，利用機器學習算法建立動力響應與缺陷信息之間的模型，從而識別結構中的缺陷大小、位置等信息是一種行之有效的方法。

2.2 機器學習模型

人工神經網絡，作為機器學習的一個模型，已經被廣泛地使用。文中利用單隱含層神經網絡建立含缺陷結構動力響應與缺陷尺寸之間的映射關系，網絡結構圖如圖4所示。特別提出，計算的動位移是在總時間為45 μs、時間增量為0.03 μs的1500個時間步下計算得到的，即每一個缺陷樣本包含1503個數據(1500個動位移數據作為輸入，2個缺陷形狀參數和1個位置參數作為輸出)，因此，訓練數據集是非常龐大的。文中利用新型的單隱含層神經網絡?極限學習機(Extreme Learning Machine，ELM)作為學習規則訓練神經網絡，ELM模型[31]由于其極快的學習速度和良好的泛化能力，大大提升了反演模型的效率，其最大的優點在于：1)輸入層和隱含層的連接權值、隱含層的閾值可以隨機設定，且設定完后無需再次調整，無需要像BP神經網絡一樣不斷反向去調整權值和閾值，因此能減少一半的運算量；2)隱含層和輸出層之間的連接權值 β無需迭代調整，可通過解方程組方式一次性確定。研究表明，通過這樣的運算規則，模型的泛化性能好，求解效率高，在保證學習精度的前提下比傳統的學習算法速度更快。

設有一個含有N個樣本的訓練集L={(xj,tj)|xj∈Rn,tj∈Rm,j=1,2,···N} ，其中xj是第j個輸入向量，tj是第j個目標輸出向量。一個含有N?個隱層節點的單隱含層神經網絡的激勵函數為：

其中：

通過分配隨機值參數wi和bj，線性系統的輸出權值可以計算為：

其中：

式中：H?為隱含層輸出矩陣H的廣義摩爾逆；β 和T分別表示輸出權矩陣和目標矩陣。

三步ELM算法可總結如下：

輸入：數據集D，隱含層神經元數目N?，激勵函數g(?)。

輸出：輸出權重β。

步驟1：隨機產生輸入權重wi和隱含層偏置bi，i=1,2,···,N?；

步驟2：計算隱含層輸出矩陣H；

步驟3：計算輸出權重β ： β=H?T。

值得指出的是，文中采用ELM作為機器學習的一個模型進行研究，但論文的思路和方法也適用于采用其他的基于人工神經網絡的機器學習模型，比如感知器神經網絡、卷積神經網絡[32]等。

2.3 缺陷反演模型

論文結合SBFEM數值模擬和機器學習算法，提出了一種薄板結構中缺陷的反演模型，該模型主要分為前處理和反演兩個階段：

1)前處理階段：在一個無缺陷薄板中隨機生成缺陷信息使其變成含缺陷薄板，并儲存缺陷信息(缺陷的位置、深度、開裂角)，同時利用SBFEM計算該缺陷薄板的觀測點處的Lamb波動力響應。此時，一個訓練樣本已經構建完畢，缺陷信息即為樣本的數據標簽，動力響應即為樣本的數據特征。如此重復構建大量的訓練樣本，形成訓練數據集。用ELM算法對訓練數據集進行學習訓練，得到一個各部分權重已確定的神經網絡(圖4中輸入層與隱含層、隱含層與輸出層之間連接權值已確定)，從而構建數據標簽與數據特征之間的關系，即動力響應與缺陷信息之間的非線性映射關系。此時整個神經網絡系統好比一個“黑匣子”，輸入一個動力響應便輸出對應的缺陷信息。

圖4 用于反演缺陷的單隱含層神經網絡結構圖Fig. 4 The structure of single hidden layer neural network for detecting flaws

2)反演階段：針對一個缺陷信息未知的薄板，通過試驗對其激發Lamb波得到觀測點處實測的動力響應，將該動力響應輸入“黑匣子”，從而獲得預測的缺陷信息。

缺陷反演模型流程如圖5所示。

圖5 反演模型實現流程Fig. 5 Flow chart of inversion model

3 數值算例

3.1 單個開口缺陷的反演

如圖6(a)所示，待研究的薄板內部缺陷形式為單個開口缺陷(具有一定開裂角和開裂深度的裂紋)，可用三個參數來近似描述這樣的缺陷，裂紋尖端坐標xc、裂紋垂向深度d和半開裂角 α。缺陷板的長度為180 mm，厚度為2 mm，彈性模量為E=200GPa ，泊松比為ν=0.3 ，密度為ρ=7850kg/m3。板為自由邊界，在板的最左端施加均勻分布的對稱脈沖荷載激發Lamb波，施加的脈沖荷載時程為：

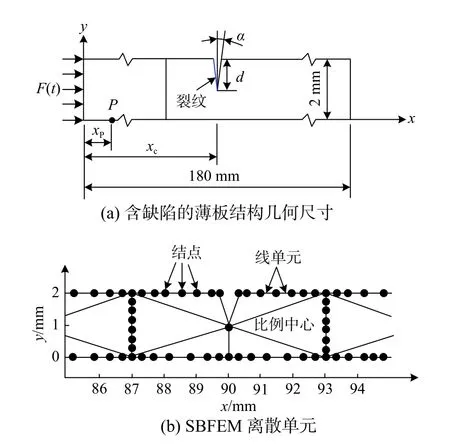
圖6 含缺陷的薄板結構幾何尺寸及SBFEM離散單元Fig. 6 The geometrical dimension of a thin plate structure with flaws and the SBFEM discretized domain

其中，f=0.6MHz ， σ=2μs ，μ=6μs。固定的信號觀測點P設置在板下表面xP=30mm處。

數值計算時，采用基于Guass-Lobatto-Legendre積分的7階線單元組成的S單元離散板的邊界，板邊界被離散成907個結點，156個線單元，31個子域，8516個自由度，離散單元的代表性部分如圖6(b)所示，連分式展開階數Mcf取5，數值計算的總時間t為45 μs，分析步時間 ?t為0.03 μs。

基于ELM進行反演分析時，將觀測點P的動位移作為單隱含層神經網絡的輸入，將3個待反演參數(裂紋尖端坐標xc、半開裂角 α和裂紋深度d)作為輸出，輸入數據被歸一化到 [0,1]范圍，隱含層神經元個數采用試錯法確定為240。本算例中，2000個隨機生成的缺陷板以及對應的觀測點動力響應樣本用于訓練單隱含層神經網絡。訓練結束后，交叉驗證采用200個缺陷板樣本，以待反演參數裂縫深度為例，這些用于交叉驗證的缺陷板裂紋深度的分布如圖7所示，可以看到，200個樣本的裂紋深度是隨機分布的，將這200個樣本的觀測點處的動力響應作為訓練好的單隱含層神經網絡的輸入數據，該網絡對輸入數據進行處理，輸出200個樣本的預測裂紋深度，然后將預測的裂紋深度與真實值進行比較，圖8給出了經過2000個樣本訓練之后的交叉驗證誤差的分布，200個樣本的交叉驗證誤差大部分在2%以下，交叉驗證的平均誤差為0.79%。因此，在交叉驗證中沒有發現明顯的過擬合現象，可以進一步利用該神經網絡預測實際缺陷板樣本的缺陷信息。

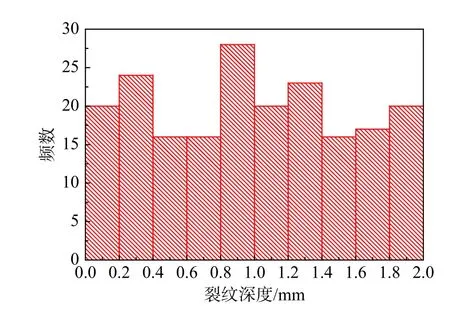
圖7 200個樣本的裂紋深度分布Fig. 7 Crack depth distribution in 200 samples

圖8 交叉驗證誤差分布Fig. 8 Cross validation error distribution

建立該神經網絡的目的是反演實際樣本的缺陷尺寸。現選取一個缺陷未知的真實樣本，圖9為實測觀測點處動力響應信號(該實測信號通過SBFEM模擬得到)，通過該實測信號利用文中建立的反演模型進行缺陷信息預測。將圖9中的動力響應信號作為訓練好的單隱含層神經網絡的輸入數據，需要說明的是，該真實樣本未在訓練過程中使用過。由于ELM的初始權重值是隨機生成的，為了避免偶然性以及象征性地表明文中反演模型的概率統計特征，反演過程采用1000次的蒙特卡洛模擬，即將反演程序連續獨立運行1000次，根據1000次模擬的統計特征來獲得反演問題的近似解。1000次蒙特卡洛模擬后的反演結果的頻率直方圖如圖10所示，橫坐標表示每個反演參數的反演值，縱坐標表示1000次模擬后該反演值出現的次數，并對1000次反演結果數據進行正態分布擬合，繪制正態分布擬合曲線，如圖中實線，并得到正態分布擬合曲線的期望值μ和標準差σ，期望值即為最后的反演結果，標準差則決定了概率分布的幅度，最終的反演結果如表1所示。

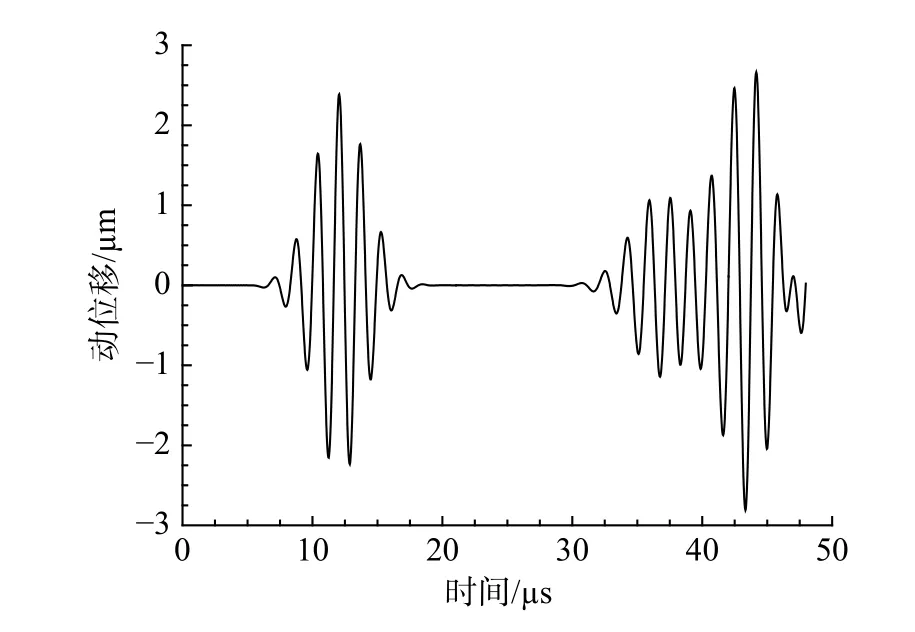
圖9 待反演缺陷的模擬量測信號Fig. 9 Simulated measurement signal of the identified defect

圖10 單個開口缺陷1000次蒙特卡洛模擬后的反演結果正態擬合頻率直方圖Fig. 10 Normal fitting frequency histogram of identified results after 1000 Monte Carlo simulations for single opening flaw

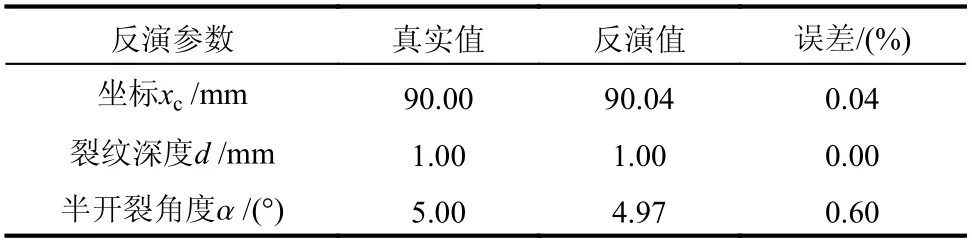
表1 單個開口缺陷的反演結果及誤差Table 1 Identified results and errors of single opening defect

可以看出，對于單個開口缺陷，建立的反演模型可以十分準確地探測出缺陷的信息。另外值得注意的是，由于ELM極快的學習速度，1000次蒙特卡洛模擬所需的時間成本極低，總計共需僅323 s左右，反演效率得到極大地提高。

3.2 兩個開口缺陷的反演

本節探討建議的反演模型對于多缺陷識別的適用性，本算例中雙裂紋板的尺寸、邊界條件、計算網格、材料參數及荷載條件同3.1節，連分式展開階數Mcf同樣取5，但板表面含有兩個開口裂紋，如圖11所示，雙開口裂紋共有6個反演參數：第一個裂紋的尖端坐標x1、裂紋深度d1、半開裂角 α1，以及第二個裂紋的尖端坐標x2、裂紋深度d2、半開裂角 α2。固定的信號觀測點P仍設置在板的下表面xP=30mm處，實測動位移信號仍通過SBFEM數值解模擬得到。

圖11 雙開口缺陷裂紋板Fig. 11 A cracked plate with two opening flaws

本算例中，仍然采用2000個隨機生成的缺陷板組以及對應的觀測點動力響應樣本用于訓練單隱含層神經網絡，最后采用經過訓練的模型預測缺陷信息。圖12為待反演缺陷板的觀測點動力響應圖，將其作為訓練好的單隱含層神經網絡的輸入數據。圖13給出了經過1000次蒙特卡洛模擬后的反演結果正態擬合頻率直方圖，最終的反演結果及誤差值如表2所示。可以看出，在進行1000次蒙特卡洛模擬之后，作為最終反演結果的概率分布期望值能很好地逼近真實結果，因此，文中提出的反演模型對于多缺陷識別也具有較好的適應性，能較準確地探測多個缺陷的位置和尺寸參數。

表2 兩個開口裂紋的反演結果及誤差Table 2 Identified results and errors of two opening flaws

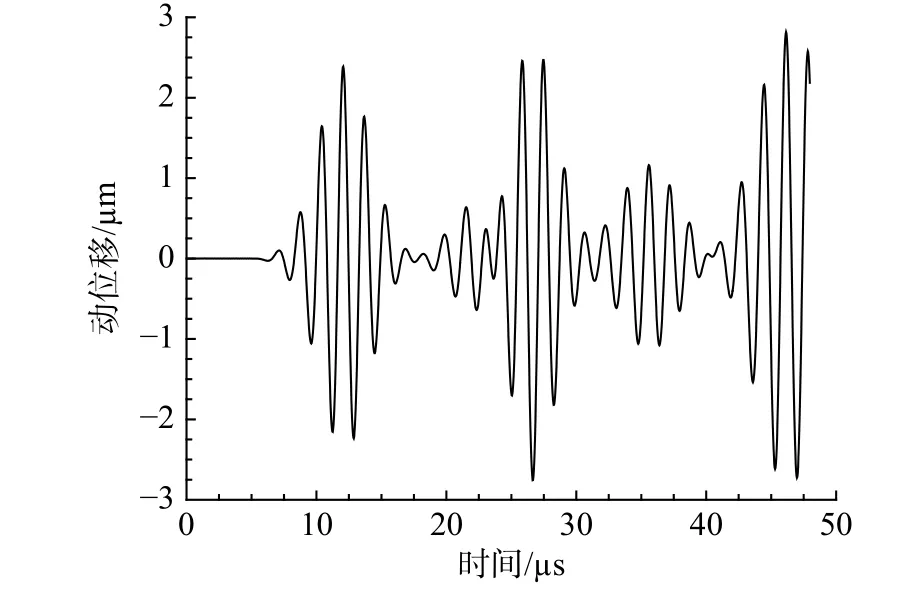
圖12 雙開口缺陷裂紋板的模擬量測信號Fig. 12 Simulated measurement signal of double-crack plate

圖13 兩個開口缺陷1000次蒙特卡洛模擬后的反演結果正態擬合頻率直方圖Fig. 13 The normal fitting frequency histogram of the identified results after 1000 Monte Carlo simulation of two opening flaws

3.3 魯棒性分析

實際問題中，傳感器測量誤差、人工測量誤差會導致測量到的動力響應信號含有一定程度的噪聲。本算例為了分析測量噪聲對缺陷參數識別的影響，考慮了測量數據中的各種噪聲污染程度，以驗證文中提出的反演模型的魯棒性。本算例同3.2，只是在通過SBFEM數值解得到的結構實際動力響應值的基礎上引入一定的高斯白噪聲來模擬有噪聲的量測動力響應信號，含噪聲的實測動位移向量um通過下式計算得到[33]：

式中：uc表示通過SBFEM計算的真實位移；ω為高斯白噪聲變量；RMSu為真實位移的均方根；p%為噪聲水平。

首先在訓練樣本中引入5%和10%的噪聲水平，并在測試信號中分別引入2%、5%、8%的噪聲水平，仍然采用2000個隨機生成的缺陷板組以及對應的含噪聲的觀測點動力響應樣本用于訓練單隱含層神經網絡，最后采用經過訓練的模型預測缺陷信息。表3、表4給出了不同噪聲水平下的最終反演結果。可以看出，文中建議的反演模型根據添加噪聲之后的動響應仍能準確地識別缺陷參數，但隨著噪聲水平的提高，反演精度會下降。

表3 訓練樣本中添加5%噪聲干擾時多缺陷參數反演結果Table 3 Multiple flaw parameter identified results when adding 5% noise interference to training samples

表4 訓練樣本中添加10%噪聲干擾時多缺陷參數反演結果Table 4 Multiple flaw parameter identified results when adding 10% noise interference to training samples

4 結論

機器學習依靠一定量的數據作為支撐，通過訓練提取出數據內部蘊藏的抽象映射關系，近年來逐漸成為計算力學領域的研究熱點。文中提出了一種結合SBFEM和機器學習的缺陷反演模型用以建立結構動響應和缺陷參數之間的映射關系。SBFEM通過改變裂紋所在子域的比例中心位置反映不同的裂紋信息，減少了需要進行重劃分的網格數量，大大提升了計算效率，能夠提供足夠多的反映缺陷特性的訓練數據；基于極限學習機的人工神經網絡機器學習模型避免了傳統反分析問題求解的目標函數極小化迭代過程，能在極快的學習速度下保證缺陷反演的精度。通過含單個和兩個開口缺陷的薄板結構數值算例，驗證了建議的反演模型可以對缺陷位置及尺寸進行精確量化且效率極高，而且該反演模型能夠在一定的噪聲水平下保持良好的魯棒性，具有工程實用性。

此外，文中提出的反演思路也可擴展到其他工程結構的缺陷檢測中，雖然反演模型有待進一步完善，比如考慮更為豐富的缺陷種類、更為復雜的結構形式，但在一定程度上反映了結合計算力學和機器學習的可行性、優越性和可挖掘性。